基于PHD濾波的多目標跟蹤及應用研究?

齊海明 張安清

（1.海軍大連艦艇學院研究生管理大隊 大連 116018）（2.海軍91202部隊 葫蘆島 125004）（3.海軍大連艦艇學院信息作戰系 大連 116018）

1 引言

傳統的多目標跟蹤是通過數據關聯技術來完成觀測數據與目標間的分配，再通過濾波技術實現目標狀態估計。典型的數據關聯目標跟蹤算法，如最近鄰、聯合概率數據關聯以及多假設跟蹤，這些算法主要存在兩方面問題，一是核心過程數據關聯運算時，隨著目標數目增多，存在組合爆炸、計算量呈指數型增長等問題［1］；二是進行多目標跟蹤時，通常假設目標數目不變，而現實常常并不滿足這個條件。

目前，Mahler提出的基于隨機有限集（Random Finite Set，RFS）理論的多目標跟蹤方法，因其能夠有效避免傳統數據關聯存在的諸多問題，同時可以實現可變目標數的估計，已成為多目標跟蹤技術發展的熱門領域。2003年，Mahler首次提出了標準的PHD濾波，該方法具有堅實的數學基礎，能更好反應目標跟蹤問題的本質，在復雜的多目標跟蹤中具有更小的計算復雜度，受到很多學者和工程技術人員的關注。

本文在回顧和介紹當前基于PHD濾波的多目標跟蹤方法的研究現狀與應用進展基礎上，對未來該領域發展的幾個重點方向提出了自己的設想。

2PHD濾波器

2.1 PHD濾波基本原理

PHD濾波算法實際是一種對后驗多目標狀態的一階矩遞推過程［2］，由于其概率密度函數的積分步驟是在單個目標的運動狀態上完成的，具有較小的運算量，相對Bayes濾波算法更容易處理。PHD濾波處理過程與傳統Bayes濾波一樣，也分為預測步和更新步，其核心思想流程如下［3］：

PHD濾波的預測方程為

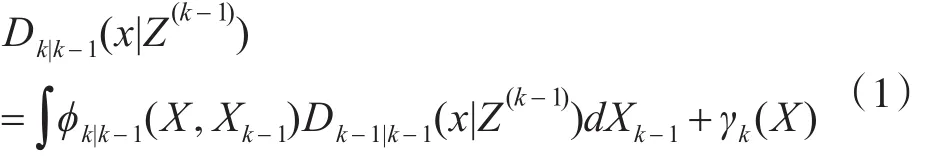
其中，?k|k-1(x，ξ)=bk|k-1(x|ξ)+ek|k-1(ξ)fk|k-1(x|ξ)，這里，bk|k-1(·|ξ)表示衍生目標集Bk|k-1({ξ})的 PHD，ek|k-1(·)表示目標存在的概率，fk|k-1(·|·)表示單目標轉移概率密度，γk(·)表示新生目標集Γk的PHD。

PHD濾波的更新方程為

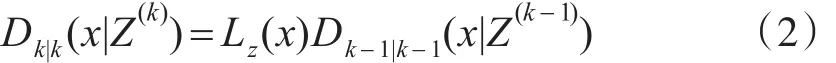
其中：

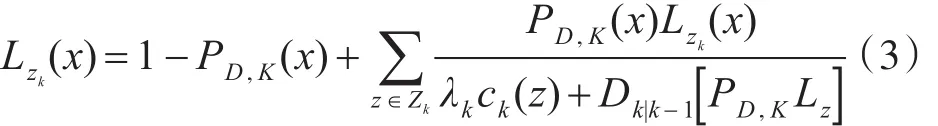
Lzk(x)表示單目標的觀測似然函數，λk表示雜波強度，ck(z)表示雜波空間分布，λkck(z)表示雜波隨機集的PHD。

其中PD，k(·)表示檢測概率。

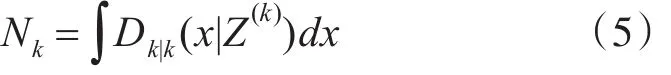
將最接近Nk的整數值作為k時刻的目標數的期望值，其目標數目估計值可表式為：峰值個數即表示目標個數。

2.2 PHD濾波器實現方法

PHD濾波更新過程中存在著復雜的積分運算，限制了PHD濾波的推廣和應用。目前主要有兩種實現方法，一是序貫蒙特卡洛法，即粒子濾波方法［2］，Vo利用序貫蒙特卡洛法產生帶有權值的隨機粒子集，以粒子分布信息對PHD近似，提出序貫蒙特 卡 洛 PHD（SequentialMonteCarloPHD，SM-PHD）濾波算法，該算法優點是可以處理非線性非高斯問題，但同粒子濾波一樣存在粒子退化的缺陷，同時還存在峰值提取困難的問題；二是高斯混合法，基于線性高斯的假設條件，Vo提出了高斯混合概率假設密度（Gaussian Mixture PHD，GM-PHD）濾波算法［4］。該算法以高斯和的形式來近似多目標PHD，假設檢測概率和存活概率與狀態無關，且衍生目標有限集和新生目標有限集的PHD均具有高斯和形式，則通過對PHD的預測更新可得到PHD遞推公式的解析解。高斯混合方法在峰值提取方面易實現，較粒子濾波方法在工程實現方面要簡單很多，計算量相對較小，計算復雜度為O(nm)，其中n為目標數目；m為觀測數目。

3 基于PHD濾波的多目標跟蹤性能評估指標

性能評估指標對濾波算法的選取、分析和評估起著很重要的作用，在進行單目標跟蹤時，我們可以用最小均方誤差法評估單目標跟蹤的性能，但對于多目標來說，由于要考慮到目標數目問題，這就需要對多目標跟蹤算法選擇更適合的評估辦法。目前，用于評價多目標跟蹤算法的性能評估方法主要有3種：Hausdorff距離，Wasserstein距離和最優子模型分配（Optimal Sub-pattern Assignment，OS?PA）距離。

Hausdorff距離對多集合之間存在的勢差不敏感，不能獲得滿意的性能評價，并且Hausdorff距離存在局限性，要求在兩個集合具有相同勢的時候，才可以采用處理。Wasserstein距離是Hoffman和Mahler基于最小平均意義下的均方根誤差距離，提出的一種優于Hausdorff距離的評價方法，但該方法存在無法處理隨機集其中一個為空集時的情況。OSPA距離是Vo研究團隊提出的一種最新評價方法，它是一種用集合間差異程度來進行衡量的誤差距離［5］。相對Wasserstein距離，OSPA距離有了很大的改進，避開了Wasserstein存在的不足。

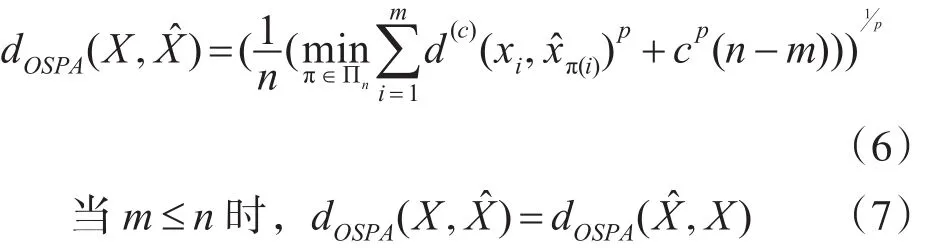
當m≥n時，

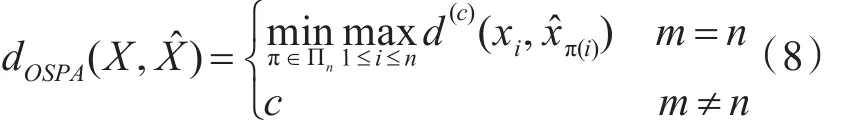
其中，d(c)(x，)=min(c，d(x，))表示x與之間的距離，c表示截取距離，p表示階數，Πk表示排列組合的集合。

4 PHD濾波在多目標跟蹤領域中的應用

近十幾年，PHD濾波在以Mahler為代表的理論研究學者和以Vo為代表的工程技術人員的不斷努力下，取得了大量研究成果。目前，PHD濾波技術已應用于很多領域的研究，如多機動目標跟蹤、弱小目標檢測前跟蹤、擴展多目標跟蹤、圖像跟蹤、群目標檢測與跟蹤、未知參數下的多目標跟蹤和傳感器管理等眾多應用，接下來對在各應用領域的突出成果進行概述。

1）多機動目標跟蹤：Vo將PHD濾波應用于多目標跟蹤，提出一種多模型PHD濾波方法，采用粒子濾波方法進行近似求解，仿真表明該方法多目標跟蹤明顯優于單模型PHD濾波［6］。Pasha等同樣將多模型方法引入到GM-PHD濾波方法中，同時考慮三種運動運動模型，在對機動目標跟蹤中表現出比傳統數據關聯IMM-JPDA（Interacting Multiple Model JPDA）更好的性能［7］。

2）弱小目標檢測前跟蹤：Punithakumar等將PHD濾波引入到紅外圖像的多目標檢測器跟蹤中，利用粒子濾波方法實現對未知目標數的弱小多目標檢測前跟蹤［8］，首次將PHD濾波思想應用于該領域研究，并通過粒子濾波實現方法驗證了該方法的可行性。Tong等通過分析傳統多目標跟蹤問題中PHD濾波方法的適用模型與假設條件，建立了“標準”多目標觀測模型，將噪聲進行泊松化，解決了雜波數目服從泊松分布的問題，仿真表明，該方法在計算量和估計精度上都優于多目標粒子濾波［9］。

3）拓展多目標跟蹤：Mahler在Gilholm等提出的量測空間模型基礎上，將PGD濾波推廣到拓展多目標跟蹤，獲得拓展目標PHD濾波器，推動了擴展多目標跟蹤技術的發展，但該算法Mahler只是進行了理論推導，沒有進行仿真實現［10］。2010年，在Vo提出的GM-PHD濾波器基礎上，Granstrom等在線性高斯假設條件下給出了拓展多目標PHD濾波器的高斯混合實現形式，通過仿真驗證了該濾波器的有效性［11］。王曉等在多模型方法啟發下，提出了一種改進的MM-GM-PHD（MultipleModel GM-PHD）來處理機動擴展多目標跟蹤的問題，取得了很好的效果［12］。

4）圖像跟蹤：Ikoma、Uchino和 Maeda將粒子PHD濾波器應用于時變光學圖像特征點跟蹤問題。Clark、Vo和Bell將GM-PHD濾波器應用于2維或3維的主動聲納圖像跟蹤問題，Wang等將粒子PHD濾波器應用于數字視頻圖像中的多目標跟蹤問題［13］。

5）群目標檢測與跟蹤：瑞典國防研究局的研究團隊在進行態勢評估模擬器系統科研實踐中，將PHD濾波器應用于PHD群目標跟蹤通過一種基于多維分配方法的編隊聚合算法對編隊結構進行檢測和分類，在每個編隊結構上采用獨立PHD濾波器進行群目標跟蹤檢測［14］。Clark等開展基于GM-PHD濾波方法的群目標跟蹤問題研究，通過創建一個具有關聯關系的目標估計狀態圖表來表示目標群，用來限制各目標高斯項在其對應的群中運動，并且通過PHD中航跡維持方法來識別目標群航跡［15］。

6）未知參數下的多目標跟蹤：連峰等開展了未知雜波背景下的多目標跟蹤研究，2009年，針對未知雜波環境問題提出一種利用有限混合模型（Fi?nite Mixture Models，FMM）和期望極大化算法對雜波模型進行估計的方法［16］，2010年，提出一種對雜波分布滿足靜態條件的多目標跟蹤方法［17］。周承興針對未知測量噪聲分布條件下提出一種基于風險評估的PHD濾波方法［18］。

7）傳感器管理：Mahler提出了一種基于PHD濾波的多傳感器多目標管理方法，該方法基于目標戰術優先級進行相對排序，可以實現對重點目標的優先觀測［19］，EL-Fallah在研究中驗證了該方法在簡化仿真場景中，可以用粒子濾波方法實現。Mahler和EL-Fallah在研究PHD濾波器改進方法中，結合未知動態變化的雜波情形，提出了計算可行的后驗期望目標數（Posterior Expected Number of Targets，PENT）公式，得到了一個統一未知動態雜波情形下的傳感器管理方法［20］。

由于PHD濾波技術在解決多目標跟蹤問題有著廣泛的前景，在國外研究的推動下，國內越來越多的研究機構和人員開始從事該領域的研究探索，主要從事PHD濾波實現方式及PHD濾波器應用等方面研究。

5 PHD濾波技術展望

縱觀上述內容，基于RFS理論的PHD濾波已經取得很多令人鼓舞的研究成果，著眼于PHD濾波的多目標跟蹤研究，現將該領域研究存在的問題以及未來重點發展的幾方面內容總結如下：

1）PHD濾波實現方法研究

目前PHD濾波的實現方法主要是序貫蒙特卡洛（粒子濾波）方法和高斯混合方法兩種，但粒子濾波方法對密度函數的選擇要求較高，同時該類函數難以確認，需要大量采樣近似計算，計算能力要求較高，較難工程實現；高斯混合方法要進行線性高斯條件假設，目前雖然一些研究者采取近似方法可以處理非線性非高斯問題，但目標估計精度有所下降，有必要開展在計算復雜度和估計精度折中的算法研究。

2）多傳感器多目標跟蹤研究

目前基于PHD濾波的多傳感器目標跟蹤通常假設各傳感器觀測數據完全獨立，采用序貫處理方式，計算復雜度小，但跟蹤精度不高、穩定性較差。另一種是采用乘積多傳感器PHD濾波方法，綜合考慮多傳感器觀測信息，具有更好的跟蹤精度和穩定性，但計算復雜度較高，難以實現。因此，如何實現精度更高、穩定更強同時易于工程實現的多傳感器多目標跟蹤是未來發展的方向。

3）多擴展目標跟蹤方法研究

目前基于PHD濾波的多擴展目標跟蹤方法大多是基于線性高斯模型的，具有一定的局限性，開展非線性非高斯的多擴展目標濾波方法研究更具有普適性，同時目前開展多擴展目標跟蹤方法研究主要是二維模型，如果能夠發展出擴展目標的三維擴展模型，則將能夠更加準確和真實地描述目標，從而獲得更多的擴展目標信息。

4）航跡生成方法研究

基于PHD濾波的多目標跟蹤算法得到的是每一時刻目標數目和目標狀態，相鄰的目標狀態之間沒有航跡關聯信息，并未給出連續時刻的目標間關系，未對所有目標的航跡進行估計。目前，基于PHD濾波的航跡生成方法主要是結合傳統數據關聯技術，將各離散時刻估計的多目標RFS視為“觀測集合”，進而采用傳統數據關聯技術形成目標航跡，但該方法并沒有考慮存在目標漏檢和虛假估計的情況，將導致形成虛假航跡和一個目標會產生多條航跡，這將不利于監視場景的綜合態勢理解和分析。未來如何在PHD濾波框架下實現聯合狀態估計及航跡生成提取是值得研究的一個方向。

5）多目標聯合檢測、跟蹤與分類方法研究

目前大多研究都將目標檢測、跟蹤與分類三個問題分開處理，然而這三個問題實際可以緊密耦合的，聯合處理有望同時得到更優異的檢測、跟蹤與分類性能。現在關于目標聯合跟蹤與分類（Joint Target Tracking and Classification，JTC）和目標聯合檢測與跟蹤（Joint Target Detection and Tracking，JDT）方面的研究有很多，但對目標聯合檢測、跟蹤與分類（Joint Target Detection，Tracking and Classi?fication，JDTC）方法研究不多，主要原因是缺乏一種既有嚴格理論解釋基礎又存在有效實現途徑的理論框架，但RFS理論的出現填補了這方面的空白，可以實現目標的檢測、跟蹤與分類同步處理，這將大大提高現代監視系統多目標信息的獲取能力，具有更大的理論和現實意義。

6 結語

本文對基于PHD濾波的多目標跟蹤發展和應用現狀進行總結概述，對PHD濾波的基本原理和實現方法進行了介紹，并對未來該方法重點發展的幾方面內容進行了展望，希望我們國內的科研人員未來在PHD濾波方面能取得更好的成就。

［1］楊峰，王永齊，梁彥等.基于概率假設密度濾波方法的多目標跟蹤技術綜述［J］.自動化學報，2013，39（11）：1944-1955.

［2］張洪建.基于有限集統計學的多目標跟蹤算法研究［D］.上海：上海交通大學，2009.31-32.

［3］李云湘.基于PHD濾波的多目標跟蹤技術研究［D］.長沙：國防科技大學，2012.33-35.

［4］Vo B-N.The Gaussian Probability Hypothesis Density Fil?ter［J］.IEEE Transaction on Signal Processing，2006，54（11）：4091-4104.

［5］張鶴冰.概率假設密度濾波算法及其在多目標跟蹤中的應用［D］.哈爾濱：哈爾濱工程大學，2012：28-29.

［6］Vo Ba-Tuong，Clark D-E，Vo Ba-Ngu.Bernoulli for?ward-backward smoothing for joint target detection and tracking［J］.IEEE Trans on Signal Processing，2011，59（5）：4473-4477.

［7］Pasha S-A，Vo B-N，Tuan H-D.A Gaussian mixture PHD filter for jump Markov system models［J］.IEEE Transaction on Aerospace and Electronic Systems，2009，45（3）：919-936.

［8］Punithakumar K，Kirubarajan T.A sequential Montel Car?lo probability hypothesis density algorithm for multitarget track-before-detect［C］//Proceedings of the 2005 SPIE，San Diego，California：SPIE，2005：587-594.

［9］Tong H-S，Zhang H，Meng H-D.Multitarget tracking be?fore detection via probability hypothesis density filter［C］//Proceedings of the 2010 International Conference on Elec?trical and Computer Engineering，Wuhan，China：IEEE，2010：1332-1335.

［10］Mahler R.PHD Filters for Nonstandard Targets，I：Ex?tended Targets［C］//The 12th International Conference on Information Fusion，Seattle，WA：IEEE，2009：915-921.

［11］Granstrom K，Lundquist C，Orguner U.Extended Target Tracking Using A Gaussian Mixture PHD Filter［J］.IEEE Transactions on Aerospace and Electronic Sys?tems，2012，48（4）：3268-3286.

［12］王曉，韓崇昭.用于機動目標跟蹤的多模型概率假設密度濾波器［J］.西安交通大學學報，2011，45（12）：1-5.

［13］王曉.基于隨機有限集的目標跟蹤方法研究及最新進展［J］.工程數學學報，2012，29（4）：567-578.

［14］Ahlberg S，Horling P，Jored K.The IDF03 information fu?sion demonstrator［C］//Processing of the 7th Internation?al Conference on Information Fusion，Sunnyvale，CA：IEEE，2004：936-943.

［15］Clark D，Godsill S.Group target tracking with the Gauss?ian mixture probability hypothesis density filter［C］//Pro?ceedings of the 3rd International Conference on Intelli?gent Sensors，Sensor Networks and Information，Mel?bourne Qld：IEEE，2007：149-154.

［16］Lian F，Han C-Z，Liu W-F.Multitarget tarcking algo?rithm in unkown clutter［J］.IEEE Transactions on Aero?space and Electronic Systems，2010，46（4）：2066-2078.

［17］連峰，韓崇昭，劉偉峰.未知雜波環境下的多目標跟蹤算法［J］.自動化學報，2010，35（7）：851-858.

［18］周承興，劉喜貴.未知測量噪聲分布下的多目標跟蹤算法［J］.航空學報，2010，31（11）：2228-2237.

［19］R Mahler.Multitarget sensor management of dispersed mobile sensor［C］//Theory and Algorithms for Coopera?tiveSystems，Singapore：WorldScientic，2005：462-471.

［20］Mahler R，El-fallah A.Unified sensor management in un?kown dynamic clutter［C］//Proceedings of the 2010 Inter?national Society for Optics and Photonics，Orlando，FL：SPIE，2010：796-803.