基于平方根濾波的GPS/INS緊組合導(dǎo)航算法優(yōu)化研究?

曲豐 張儀 吳磊

（91388部隊 湛江 524022）

1 引言

INS和GPS緊組合導(dǎo)航系統(tǒng)具有優(yōu)勢互補的特點，以適當?shù)姆椒▽烧呓M合起來使用，取長補短，可以克服GPS接收機的性能問題包括對外界干擾源的易感染、第一次位置的結(jié)算時間、由遮蔽引起的衛(wèi)星信號中斷、完好性、信號重新捕獲能力。和慣性導(dǎo)航系統(tǒng)傳感器長時間未校準導(dǎo)致的精度惡化、價格昂貴等缺點，構(gòu)成了一種增效的關(guān)系。這兩種類型的導(dǎo)航系統(tǒng)的組合不僅克服了使用單一導(dǎo)航系統(tǒng)出現(xiàn)的性能問題，同時也形成了一種性能超過了任何一個單一的導(dǎo)航系統(tǒng)的新系統(tǒng)。即組合后導(dǎo)航精度高于INS和GPS單獨使用的導(dǎo)航精度［1］。因為當慣性導(dǎo)航系統(tǒng)的導(dǎo)航誤差隨著時間的增加而逐漸增大時，GPS導(dǎo)航系統(tǒng)可以提供有界的精度，不僅限制了導(dǎo)航誤差的持續(xù)增大，而且能夠校準慣性導(dǎo)航系統(tǒng)。然而，由于描述系統(tǒng)的動力學(xué)特性的數(shù)學(xué)模型和噪聲的統(tǒng)計模型不夠準確，不能夠真實的反應(yīng)物理過程，從而使模型與獲得的量測值不匹配。同時，卡爾曼濾波是遞推的過程，隨著濾波步數(shù)的增加，舍入誤差逐漸積累，如果計算機的字不夠長，這種積累誤差有可能使估計的均方誤差陣失去非負定性或者對稱性，使增益陣的計算值逐漸失去合適的加權(quán)作用，

兩者均可導(dǎo)致而卡爾曼濾波器發(fā)散。為了克服這種發(fā)散的現(xiàn)象，改善卡爾曼濾波數(shù)值的穩(wěn)定性，并提高計算效率［2］。在本文中提出了平方根濾波算法。

2 GPS/INS組合緊導(dǎo)航系統(tǒng)理論基礎(chǔ)

GPS導(dǎo)航系統(tǒng)和慣性導(dǎo)航系統(tǒng)的緊組合是通過使用卡爾曼濾波器來實現(xiàn)的［3］。它是把各類傳感器捕獲的導(dǎo)航信息提供給濾波器，運用卡爾曼濾波的方法進行信息處理，得到慣性導(dǎo)航系統(tǒng)誤差的最優(yōu)估計，再對組合導(dǎo)航系統(tǒng)進行校正，進一步提高導(dǎo)航精度。

緊組合導(dǎo)航是一種相對比較復(fù)雜的GPS/INS組合導(dǎo)航方式。是從接收機中提取原始的偽距和偽距率信息，通過觀測衛(wèi)星星歷數(shù)據(jù)，將INS的積累誤差映射成用戶至衛(wèi)星的視距誤差，并且根據(jù)偽距和偽距率殘差觀測方程進行濾波，對INS的誤差進行估計、校正。緊組合導(dǎo)航系統(tǒng)主要由GPS子系統(tǒng)、INS子系統(tǒng)和卡爾曼濾波器三部分組成［4］。其中INS子系統(tǒng)中INS導(dǎo)航解算組件接受的IMU輸出的比力和角速度信息，產(chǎn)生INS的導(dǎo)航輸出信息，即位置和速度，并結(jié)合GPS子系統(tǒng)產(chǎn)生的星歷可以解算出INS的偽距和偽距率；INS和GPS子系統(tǒng)產(chǎn)生的偽距和偽距率作差值并作為卡爾曼濾波器的輸入，得到INS的狀態(tài)誤差估計值；再將估計值中的陀螺儀誤差和加速度計誤差反饋給INS系統(tǒng)對其進行修正，把狀態(tài)誤差估計值中的位置和速度誤差對INS解算后的位置和速度信息進行校正，輸出即為緊組合導(dǎo)航系統(tǒng)的最終導(dǎo)航信息［5］。具體原理框圖1如下。

圖1 緊組合導(dǎo)航系統(tǒng)原理框圖

3 組合導(dǎo)航平方根濾波算法

3.1 卡爾曼濾波器系統(tǒng)模型

卡爾曼濾波器運用的工程對象一般都是連續(xù)的系統(tǒng)，考慮到計算機的實現(xiàn)過程，經(jīng)常用離散化模型來描述系統(tǒng)，離散化后的系統(tǒng)的動態(tài)模型如下［6］：

系統(tǒng)狀態(tài)方程：

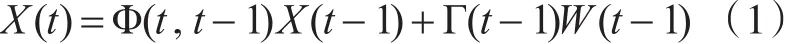
量測方程：

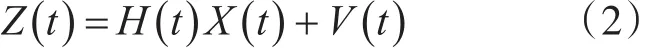
公式中，X(t)是t時刻系統(tǒng)的n維狀態(tài)向量，卡爾曼濾波的目的就在于對狀態(tài)向量進行最佳估計，Z(t)為t時刻系統(tǒng)的m維觀測向量。是系統(tǒng)t-1到t時刻的一步轉(zhuǎn)移矩陣階。是系統(tǒng)的噪聲矩陣階；它表示的含義是t-1時刻到t時刻的各個系統(tǒng)噪聲分別影響t時刻各個狀態(tài)的程度。是系統(tǒng)t-1時刻的噪聲向量（r維）；是t時刻的量測矩陣階；是t時刻的m維噪聲量測向量。

在建立狀態(tài)轉(zhuǎn)移方程和觀測方程后，卡爾曼濾波器要求系統(tǒng)噪聲和量測噪聲必須是相互獨立的零均值白噪聲序列，即：

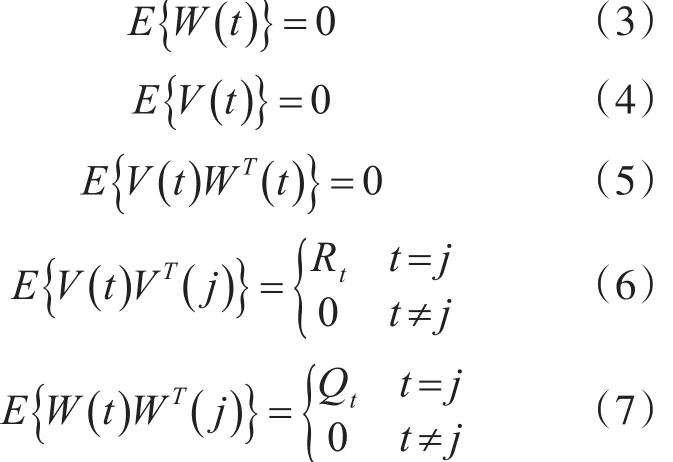
預(yù)測誤差向量定義為

教師進修學(xué)校要聯(lián)合教研室、電教儀器站以及基地實驗學(xué)校對口薄弱學(xué)校 “多位一體”共建校內(nèi)外網(wǎng)絡(luò)環(huán)境。以進修學(xué)校為主導(dǎo)，其他機構(gòu)負責聯(lián)合搭建后期培訓(xùn)服務(wù)支持體系，在網(wǎng)絡(luò)平臺上通過班級沙龍自由討論，讓所有參訓(xùn)教師圍繞與當次培訓(xùn)相關(guān)的一個主題開展活動，活動可以由學(xué)科專家一人主講眾人提問，也可以眾人提問，由專家對活動中遇到的具體實踐問題一一做出解答。

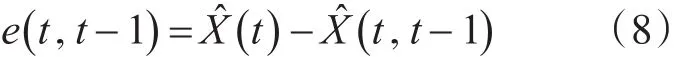
預(yù)測誤差的相關(guān)矩陣定義為

當輸入t時刻Z（t）時，帶來的新信息是被稱為新息向量。

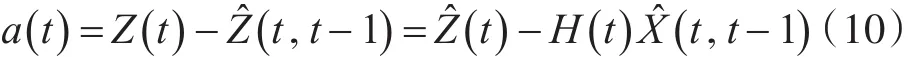
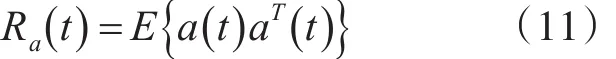
卡爾曼濾波的增益：

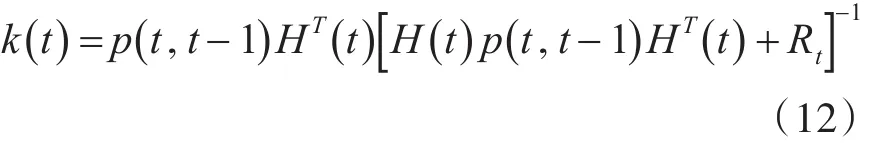
其中，Qt為系統(tǒng)噪聲的維方差矩陣，Rt為量測噪聲的維方差矩陣。在卡爾曼濾波的過程中，要求它們分別為已知值得非負定矩陣和正定矩陣。

3.2 緊組合導(dǎo)航平方根濾波算法建模

卡爾曼濾波器是基于最小均方誤差估計導(dǎo)出來的。是對狀態(tài)矢量在最小均方估計誤差的最佳估計。但在工程運用中，該算法容易發(fā)散，基于次，本文中引入平方根濾波算法。平方根濾波算法與一般的最小二乘方法不同，在經(jīng)典卡爾曼濾波中，狀態(tài)均方差陣P(t)表示的是狀態(tài)估計誤差的平方。平方根濾波方法主要是針對均方差陣更新過程設(shè)計，采用喬萊斯基分解法分解均方差陣，對平方根進行更新，以減少計算誤差。

3.2.1 均方差陣的量測更新

將增益公式代入卡爾曼濾波量測公式，得

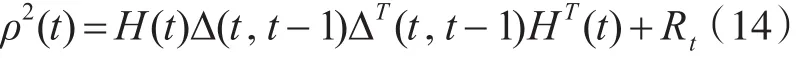
可得均方差量測更新公式

其中γ(t)為待定系數(shù)，由均方差量測更新公式可求得：

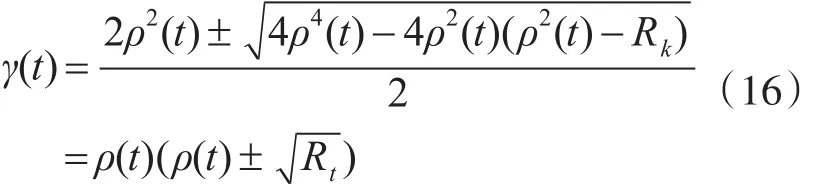
3.2.2 均方差陣狀態(tài)更新

將 Δ(t)，Δ(t-1)，Δ(t，t-1)代入卡爾曼濾波的狀態(tài)公式，可得均方差陣的狀態(tài)更新為

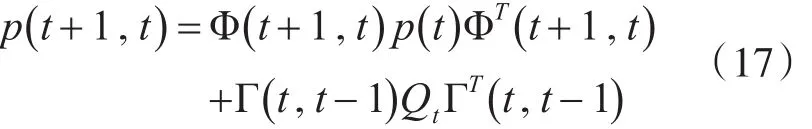
同時簡記

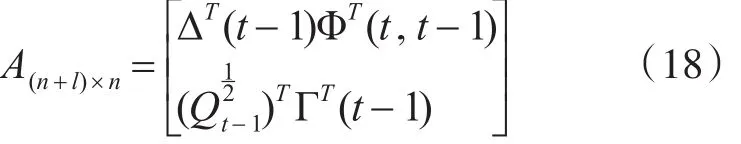
可求得

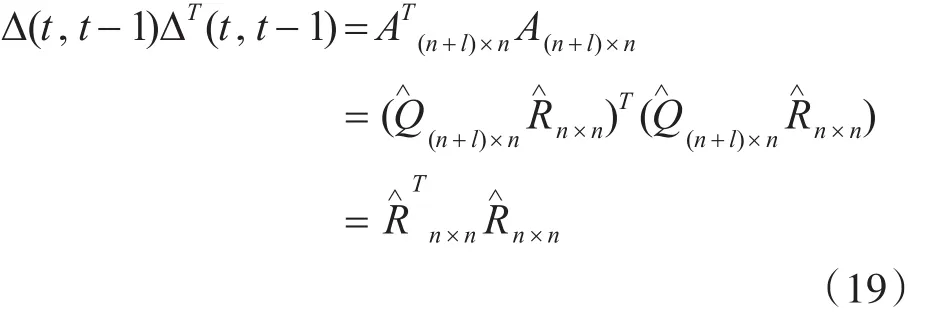
3.2.3 平方根濾波流程

若簡記

則由式（14）、（15）及濾波增益公式，可分別得

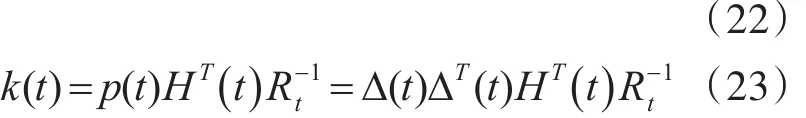
至此，卡爾曼平方根濾波流程可總結(jié)如圖2所示。

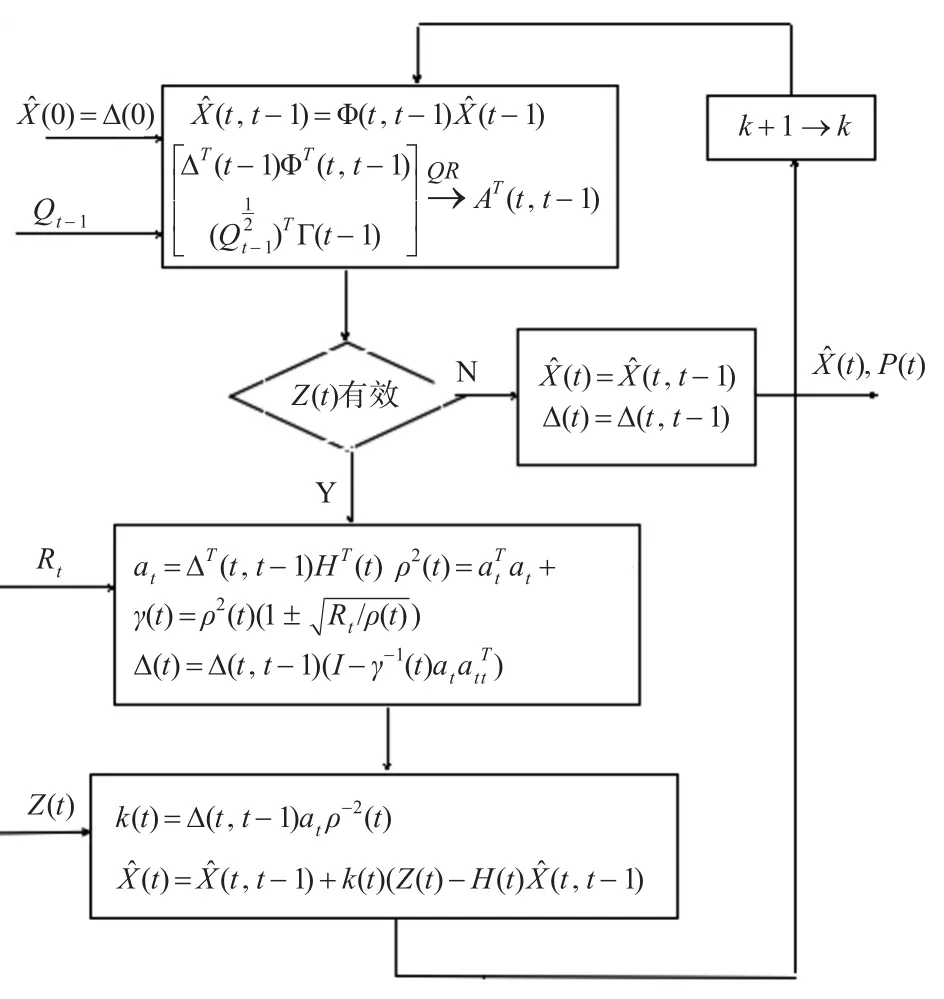
圖2 平方根濾波流程

其中，初始化時輸入為狀態(tài)均方差陣的平方根Δ(0)，濾波過程采用平方根更新算法，濾波迭代運算的是均方差陣平方根Δ(t)，若想輸出均方差陣P(t)，作平方運算即可。

4 仿真實驗與結(jié)果分析

4.1 載體軌跡生成

任何一條載體的運動軌跡都可以用多項式來逼近，在地心固定直角坐標系中，載體的運動軌跡可以用n次多項式準確描述［7］。本文中假設(shè)載體在地心固定直角坐標系的位置用2次多項式的函數(shù)變化，其位置表示為

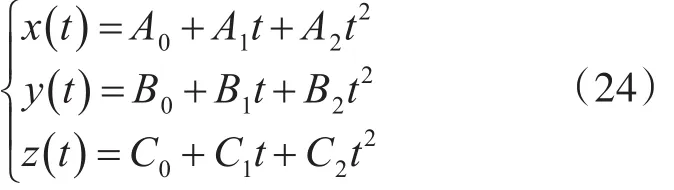
在仿真實驗前，需要對載體運動軌跡參數(shù)的初始值進行設(shè)定，這里給定載體軌跡初始的狀態(tài)參數(shù)如下：

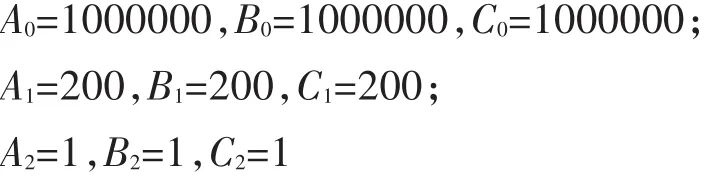
4.2 仿真結(jié)果與分析

采用上述載體航跡作為本次組合導(dǎo)航算法的仿真航跡，提取真實的星歷參數(shù)和當前接收機載體的航跡產(chǎn)生一個模擬的偽距和偽距率信息進行緊組合導(dǎo)航的卡爾曼濾波算法和平方根濾波算法進行仿真實驗［8］。在偽距上添加均方差為10m，均值為0的高斯白噪聲和10m的等效鐘差。在偽距率上添加標準差為1m/s，均值為0的高斯白噪聲和時鐘相關(guān)時間為1800s。并且在可用星數(shù)目一直大于4個的條件下，在進行仿真時，將采用無反饋式組合導(dǎo)航進行仿真。忽略一階馬爾科夫過程噪聲，設(shè)定陀螺儀的常值漂移誤差為2°/h，白噪聲均方差為0.1°/h。在加速度計中添加100μg的零偏誤差和10μg的驅(qū)動白噪聲均方誤差。仿真時長設(shè)定為600 s，設(shè)定慣性導(dǎo)航系統(tǒng)輸出頻率100Hz，GPS導(dǎo)航系統(tǒng)輸出頻率為10Hz，組合導(dǎo)航系統(tǒng)輸出頻率100Hz。并且對仿真實驗結(jié)果進行比較和分析，仿真結(jié)果如圖4所示。

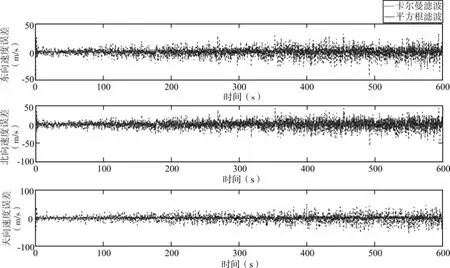
圖3 速度誤差結(jié)果

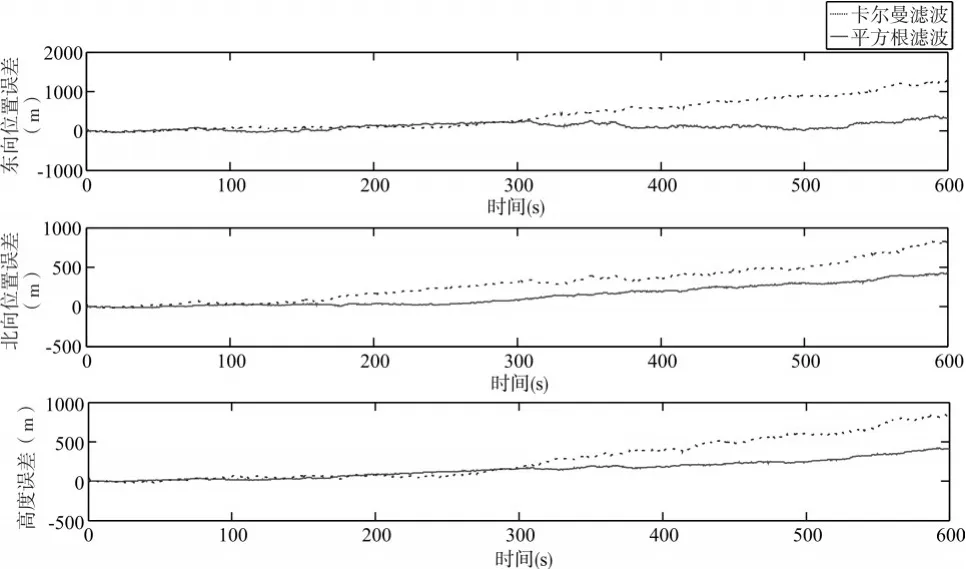
圖4 位置誤差結(jié)果

通過仿真實驗結(jié)果圖3、圖4可以分析出，采用平方根濾波算法進行緊組合導(dǎo)航時，速度誤差沒有像傳統(tǒng)的卡爾曼濾波算法一樣有較為明顯的誤差跳變。平方根濾波算法定速精度較傳統(tǒng)的組合導(dǎo)航算法定速精度有所提高，其導(dǎo)航位置、速度誤差均小于緊組合導(dǎo)航方式中的卡爾曼濾波算法的位置、速度誤差，導(dǎo)航效果高于傳統(tǒng)卡爾曼濾波的導(dǎo)航方式。有效的抑制了導(dǎo)航誤差的發(fā)散。

5 結(jié)語

本文著重針對緊組合導(dǎo)航算法進行了研究嗎，以傳統(tǒng)的卡爾曼濾波算法為基礎(chǔ)，提出了一種基于平方根濾波的組合導(dǎo)航算法。通過均方差矩陣的平方根分解，對傳統(tǒng)的算法進行了改進［9～11］。實驗結(jié)果表明，平方根濾波可較好的提高了緊組合導(dǎo)航系統(tǒng)的定位、定速的能力，減小了隨機誤差對系統(tǒng)定位、定速的影響，具有較好的實用性［12］。

［1］劉江，蔡伯根.一種組合導(dǎo)航的自適應(yīng)信息融合算法［J］.北京交通大學(xué)學(xué)報，2008，32（2）：88-93.

［2］楊莉.基于GPS/SINS組合導(dǎo)航算法的優(yōu)化設(shè)計與仿真［D］.北京：中國科學(xué)院大學(xué).2015.

［3］高為廣，等.GPS導(dǎo)航中的抗差自適應(yīng)Kalman濾波算法［J］.測繪科學(xué)，2005，30（2）：98-100.

［4］黃云乾，等.基于GPS/INS緊組合導(dǎo)航姿態(tài)計算方法選取分析［J］.測繪通報，2015，5：63-65.

［5］張闖.改進GPS/SINS新息自適應(yīng)交互多模的組合導(dǎo)航濾波算法［J］.空軍工程大學(xué)學(xué)報，2015，16（6）：11-16.

［6］曹昇杰.基于SINS/GPS的組合導(dǎo)航系統(tǒng)與濾波算法研究［D］.廣州：華南理工大學(xué)，2016.

［7］張宏啟.新型自適應(yīng)kalman濾波算法在組合導(dǎo)航中的應(yīng)用研究［D］.哈爾濱：哈爾濱工程大學(xué)，2011.

［8］方琳.徐曉蘇.自適應(yīng)濾波器在組合導(dǎo)航系統(tǒng)中的應(yīng)用［J］.艦船電子工程，2007，27（6）：69-73.

［9］劉廣軍.組合導(dǎo)航系統(tǒng)的數(shù)據(jù)處理與仿真［D］.鄭州：解放軍信息工程大學(xué)，2002.

［10］徐田來，游文虎，崔平遠.基于模糊自適應(yīng)卡爾曼濾波的INS/GPS組合導(dǎo)航系統(tǒng)算法研究［J］.宇航學(xué)報，2005，26（5）：571-575.

［11］樂洋，何秀鳳.區(qū)間自適應(yīng)kalman濾波算法在GPS/INS組合導(dǎo)航中的應(yīng)用.大地測量與地球動力學(xué)［J］.2010，30（2）：113-116.

［12］劉曉光，胡靜濤，王鶴.基于自適應(yīng)H∞濾波的組合導(dǎo)航方 法 法 研 究［J］.儀 器 儀 表 學(xué) 報 ，2014，35（5）：1013-1021.