距離多普勒耦合對雷達濾波精度影響分析?

李國君 趙棟華 趙永鐵

（中國人民解放軍92941部隊 葫蘆島 125001）

1 引言

雷達系統作為現代導彈武器系統重要前端，具有感知目標的關鍵作用，是武器系統的“千里眼”和“順風耳”。現代戰爭條件下，要求雷達既要看得遠又要看得準，雷達看得遠要求發射信號為寬脈沖，寬脈沖在提高雷達威力的同時將帶來雷達分辨率下降的負面影響，為解決雷達威力與分辨率的矛盾，現代雷達系統多采用脈沖壓縮技術。線性調頻脈沖壓縮體制具有對多普勒頻移不敏感［1］的特點，即相對固定載頻而言，目標回波載頻的變化是多普勒頻移和線性調頻本身變化量雙重作用的結果。因此線性調頻脈沖壓縮信號在雷達信號中應用最廣泛，但引入的問題是匹配濾波器輸出響應將出現與多普勒頻移成正比的附加延時，即距離多普勒耦合現象［2］。

本文主要研究在雷達數據處理階段，距離多普勒耦合對雷達濾波的影響，主要研究對濾波數學模型、濾波精度等方面影響問題。

2 距離多普勒耦合系數

雷達發射電磁波被目標散射后，由接收天線進行接收，并經兩次變頻至中頻后進行信號檢測，目前通常的信號檢測方法是利用匹配濾波器完成信號檢測［3］。線性調頻信號是載頻為線性變化矩形脈沖。若脈沖寬度為τ0，載波中心頻率為f0，頻率從f1變化至f2，則匹配濾波器的時延輸出為頻率的線性函數，可表示為

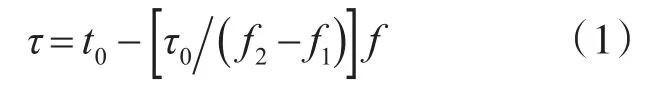
其中，t0為匹配濾波器的固有時延。

由于多普勒頻移的影響，在匹配濾波器的輸出響應中，增加了多普勒頻移的輸出，即

v為目標運動徑向速度。

由此引入的時延為

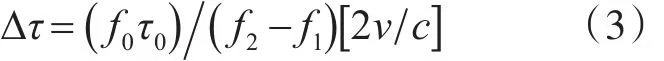
令

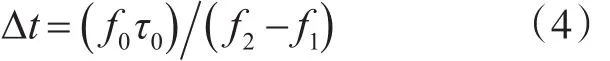
Δt為描述距離多普勒耦合程度的參數，稱之為距離多普勒耦合系數［4～6］。

3 考慮耦合效應的雷達濾波過程

當目標散射回波信號經匹配濾波器檢波并經門限檢波后，得到目標的距離信息，同時經單脈沖測角得到目標的角度信息，距離微分或多普勒濾波后得到目標的速度信息。在得到目標的四維信息后，雷達數據處理完成目標航跡起始、航跡相關［7］并在雷達顯示終端上進行顯示［8～9］。根據信號處理速度要求，目標航跡數據預測、相關和外推等算法目前多可采用Kalman濾波、α-β-γ濾波或綜合采用上述兩種濾波方法。

本文從α-β-γ濾波入手分析距離多普勒耦合效應對濾波的影響。Kalman濾波與α-β-γ濾波的主要區別其濾波增益矩陣是時變的，其它濾波過程均相同［10～11］，距離多普勒耦合對α-β-γ濾波影響的分析方法適用于對Kalman濾波影響分析。

3.1 α-β-γ濾波

α-β-γ濾波器用于對勻加速目標的跟蹤，系統狀態方程［4～5］為

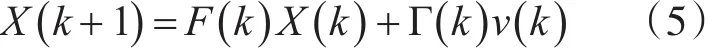
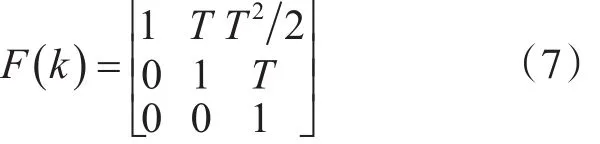
其中：T為采樣間隔。

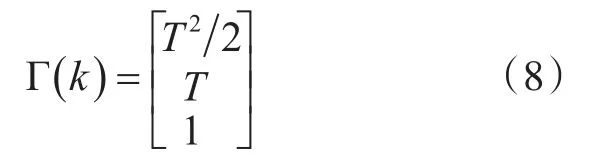
系統量測方程為

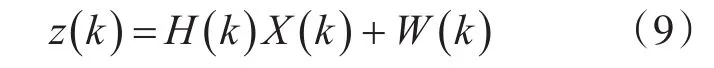
量測矩陣H為

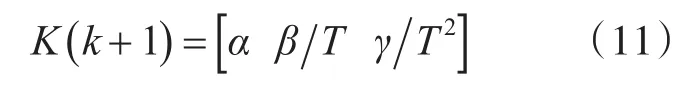
其中，工程上α、β和γ一般采用經驗參數值，本文采用多項式擬合方法［12］確定濾波增益參數值，即

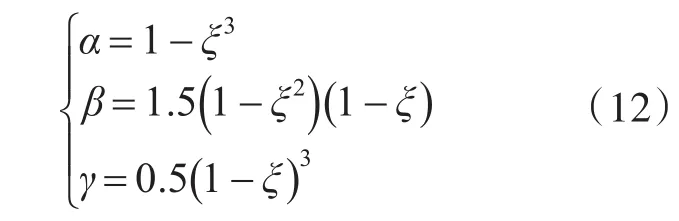
其中：0＜ξ＜1。

在實際工程應用中，對于不同的狀態噪聲和量測噪聲，ξ取值不同有可能導致濾波發散。

3.2 考慮距離多普勒耦合的α-β-γ濾波

當存在距離多普勒耦合時，α-β-γ濾波器量測矩陣H變為H′，其形式為

Δt即為式（4）中距離多普勒耦合系數。α-β-γ濾波器的其它數學模型均不變。

為分析距離多普勒耦合對α-β-γ濾波的影響，引入距離、速度和加速度的均方根誤差Δ，其數學形式為

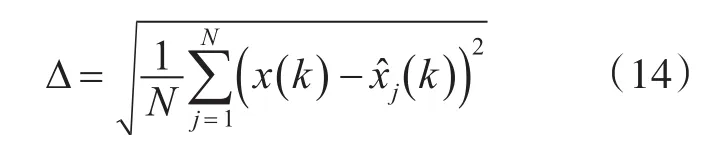
其中：N為Monte-Carlo仿真次數，為k時刻目標狀態（距離、速度和加速度）真實值（根據狀態方程得出），為目標狀態濾波估計值［13］。

4 仿真分析

4.1 仿真條件

假設某型雷達發射脈沖載頻f0=5GHz，脈沖寬度分別為τ0=10、40 μs，調頻帶寬B=1MHz，則距離多普勒耦合系數Δt分別為0.05和0.2。為評估距離多普勒耦合對濾波估計的影響，采用2000次Monte-Carlo仿真分析，狀態噪聲方差，量測噪聲方差。為保證α-β-γ濾波器收斂速度和跟蹤精度，在給定上述狀態噪聲和量測噪聲情況下，ξ取值為0.5。

假設目標沿雷達徑向作勻速直線運動，目標初始狀態值為距離100km、速度200m/s、加速度0.5m/s2。目標持續運動時間為100s，采樣間隔為1s，初始估計值取第一次量測值。當采用本文的濾波精度分析方法時，目標初始狀態值對仿真結果分析沒有影響，因此目標初始狀態值可根據實際情況靈活選取。

圖3～5分別為距離多普勒耦合系數Δt分別為0、0.05和0.2時，kalman濾波器輸出的距離、速度和加速度濾波均方根誤差。

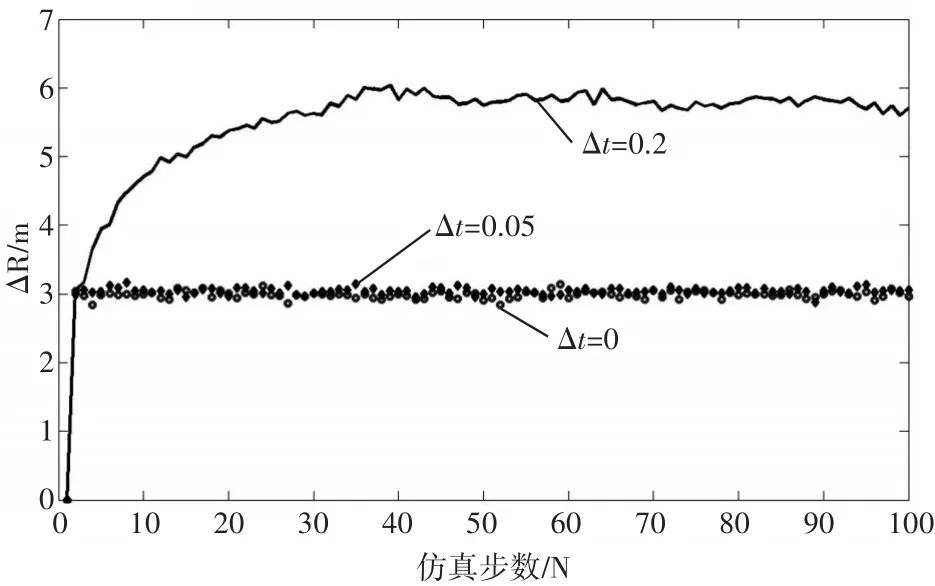
圖3 距離均方根誤差

圖4 速度均方根誤差

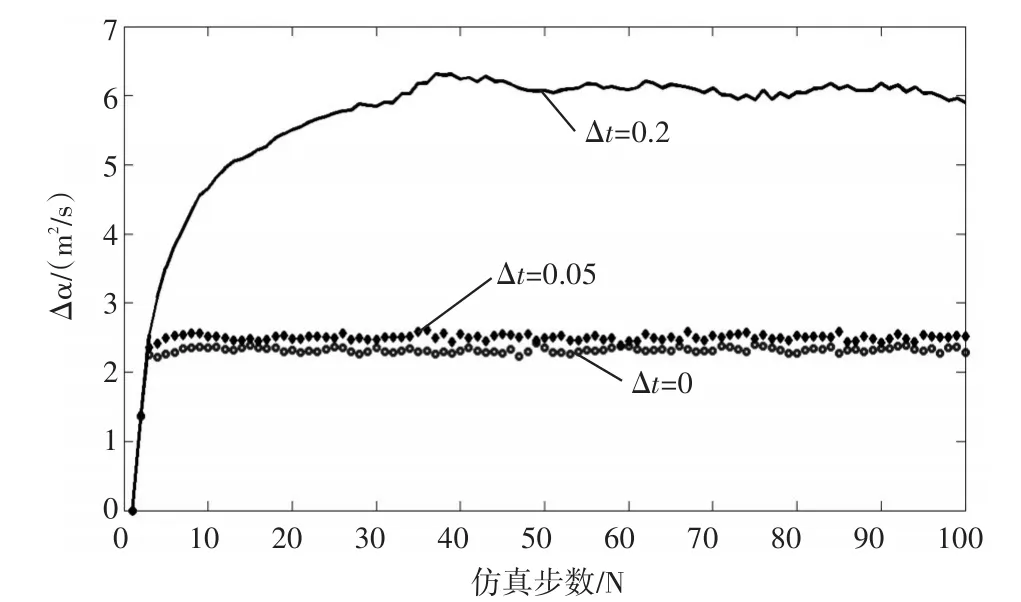
圖5 加速度均方根誤差

4.2 仿真結果分析

根據仿真結果，可得出如下結論：

1）在系統狀態噪聲和量測噪聲一定的情況下，在距離多普勒耦合系數分別為0和0.05時，α-β-γ濾波器濾波精度會發生微小的變化，很多情況下可以忽略。

2）距離多普勒耦合系數對α-β-γ濾波影響存在一臨界點，當耦合系數大于該臨界點時，濾波精度精度（距離、速度和加速度）急劇變差，在圖3～5中，距離多普勒耦合系數取0.2時，α-β-γ濾波器濾波精度急劇變差，該系數進一步增大時，微小的耦合系數增量將導致濾波迅速發散。

3）為避免距離多普勒耦合對雷達數據處理的影響，根據距離多普勒耦合數學模型，按照目前電子器件發展水平，比較可行的技術手段是增大線性調頻信號帶寬。

5 結語

距離多普勒耦合是線性調頻信號經匹配濾波的固有產物，本文從α-β-γ濾波器出發，研究了該問題對雷達數據處理過程中濾波精度的影響，該問題分析思路具有通用性，經適當修正后適用于絕大多數濾波算法。同時需要指出的是距離多普勒耦合對雷達信號處理同樣會產生不利影響，如直升機螺旋槳、噴氣式飛機發動機葉片等均會產生距離多普勒耦合，造成目標回波信號包絡畸變［14］，因此本文分析的距離多普勒耦合效應具有重要的工程意義。

［1］胡紅軍.脈沖壓縮雷達距離多普勒耦合對測距影響分析［J］.現代雷達，2011，33（12）：47-50.

［2］王元愷，肖澤龍，許建中，等.一種改進的FMCW雷達線性調頻序列波形［J］.電子學報，2017，45（6）：1288-1293.

［3］朱文濤，蘇濤，楊濤，等.線性調頻連續波信號檢測與參數估計算法［J］.電子與信息學報，2014，36（3）：552-558.

［4］趙鋒，王雪松，肖順平.高耦合系數條件下徑向速度測量的新方法［J］.信號處理，2008，24（3）：460-463.

［5］ROBERT.Effects of Range-Doppler Coupling on Chirp Radar Tracking Accuracy［J］.IEEE TRANSACTIONS ON AEROSPACE AND ELECTRONIC SYSTEMS，1974，10（4）：528-532.

［6］Trofimenko.Influence of range-Doppler coupling on the tracking stability of reentering space objects［C］//2015 In?ternational Conference on Engineering and Telecommuni?cation，41-44.

［7］鄭嘯宇，王建衛.基于LFM的雙波段雷達航跡起始方法［J］.現代雷達，2016，38（8）：54-58.

［8］左現剛，武變霞，王建平，等.一種改進的基于交互式模型的機動目標跟蹤算法［J］.火力與指揮控制，2016，41（11）：41-44.

［9］瞿冬霞.LFM脈沖雷達回波模擬和處理的研究［D］.南京：南京理工大學，2010.

［10］何友，修建娟，張晶煒，等.雷達數據處理及應用［M］.北京：電子工業出版社，2006.

［11］賀若飛，田雪濤，劉宏娟，等.基于蒙特卡羅卡爾曼濾波的無人機目標定位方法［J］.西北工業大學學報，2017，35（3）：435-441.

［12］崔嵬，朱新國，沈清.一種新的三階距離跟蹤環參數設計算法［J］.兵工學報，2010，31（6）：807-810.

［13］楊永建，樊曉光，王晟達，等.基于修正卡爾曼濾波的目標跟蹤［J］.系統工程與電子技術，2014，36（5）：846-851.

［14］D.C.Ross，J.L.Vo lakis and H.T.Anastassiu Effi?cient Computation of Radar Scattering Modulating from Jet Engines［J］.Radio Science，1996，4：991-997.