直升機槳葉結構載荷校準過程中的預扭角確定方法

王澤峰 寇福軍

摘要：給出了一種直升機槳葉結構載荷校準過程中的預扭角確定方法。首先，介紹了試驗原理，試驗設計為在槳葉擺振方向小角度范圍內加載，計算槳葉剖面在擺振方向加載時對應剖面的揮舞彎矩輸出，在線彈性范圍內，理論分析了揮舞彎矩電橋的輸出結果與擺振豎直方向角度的線性關系；其次，以某型直升機槳葉為例，應用電阻應變計法，采用機載CAM500系列測試設備，完成了對其槳葉剖面預扭角的確定實踐，驗證了方法的正確性和準確性，為直升機槳葉結構載荷校準提供技術支持。

關鍵詞：直升機；槳葉；預扭角；結構載荷；載荷校準

中圖分類號：V216

文獻標識碼：A

DOI：10.19452/j.issn1007-5453.2018.01.042

直升機槳葉在旋轉過程中，主要的運動有揮舞運動和擺振運動，揮舞和擺振本是兩個方向的自由度，但在實際運動過程中，揮擺運動往往是耦合的，即揮舞運動與擺振運動互為影響，表現在結構上就是揮舞形變與擺振形變互為影響。反映在結構承載上就是揮舞彎矩和擺振彎矩互為影響，因此，揮、擺彎矩較難測量。直升機槳葉在進行結構載荷測量時，也是采用電阻應變計法，在地面完成載荷校準之后進行實測。而在載荷校準過程中，如何精準地確定校準剖面的預扭角是最為關鍵的第一步，其直接影響后續的載荷校準結果，因此，確定預扭角的方法研究非常有意義。國內外關于槳葉在載荷校準過程中的預扭角確定方法大多在理論階段。本文結合某型直升機旋翼部件載荷測量，首先通過理論分析了一種試驗原理，然后應用電阻應變計法，進行該型直升機槳葉的預扭角確定方法工程實踐。

1原理介紹

圖1為槳葉安裝角示意圖，其中，a為翼型剖面的弦線與槳轂平面的夾角，即為槳葉安裝角。槳葉在設計時，考慮氣動效率的原因，從槳根到槳尖部分，各剖面的安裝角呈一定規律分布，總體趨勢為槳根處安裝角大于槳尖處安裝角。槳葉在載荷校準之前需要確定的預扭角即為安裝角。

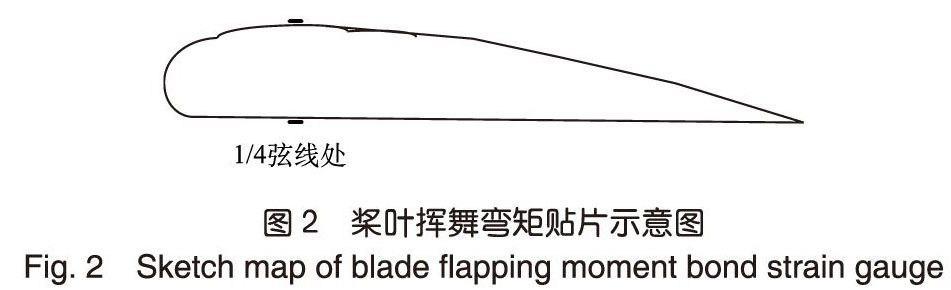
對于現代復合材料槳葉而言，其承載大梁一般為距離翼型前緣1/4處，因此，測量揮舞彎矩的電阻應變計一般的貼片位置為距離前緣1/4處的槳葉上翼面和下翼面處，如圖2所示。

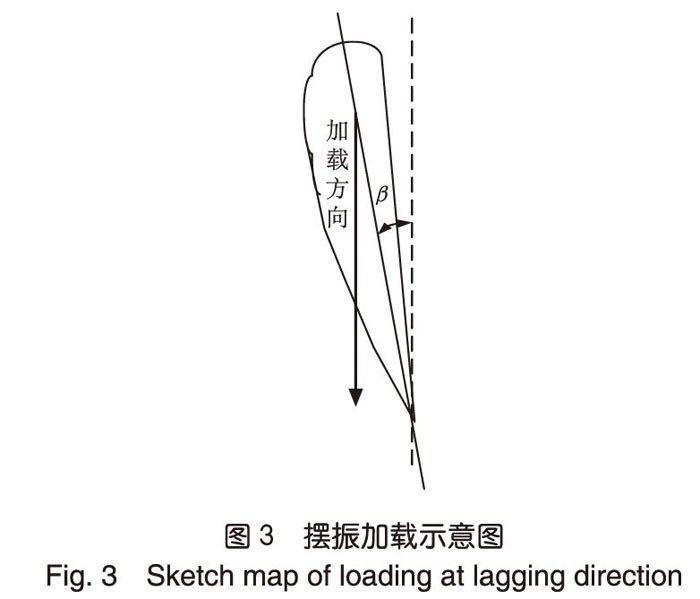
預扭角確定的思路：將槳葉調整至豎直位置，即擺振方向，使槳葉弦向與豎直方向呈一定角度β0，在加載端加載后記錄槳葉揮舞電橋的輸出a0，加載示意圖如圖3所示。以一定增量依次改變β的角度，采用同樣的方式，記錄揮舞電橋的輸出，繪出揮舞電橋隨β的變化曲線，可得擬合曲線如下：

p=ka+b

（1）式中：k為擬合系數，b為擬合直線的截距。

當揮舞電橋的輸出為0時，對應的角度β即為該剖面的預扭角，6為對應剖面的擬合預扭角。

該過程中有兩個問題需要說明：

（1）實測得到的揮舞電橋輸出a為該剖面揮舞彎矩產生的應變，由材料力學可知梁剖面的應變計算公式如下：式中：k為常量，M揮舞為彎矩，h為距離，I為慣性矩。可知在該加載過程中，揮舞電橋的輸出a和揮舞方向的彎矩M為一一對應關系，當電橋輸出為0時，意味著揮舞方向承載彎矩為O。

（2）假設槳葉加載端距離該揮舞電橋端的距離為r，加載端力的大小為F，由圖3可以得到，在擺振方向加載時，實際加載產生的揮舞彎矩為F×r×sinB≈F×r×B（β≤1°），是為彎矩小量。同時，隨著β的減小，揮舞彎矩同樣減小，甚至可能等于O。其次，隨著β以一定的增量△β變化，在小角度范圍內，新加載產生的揮舞彎矩為F×r×（β+△β）。可以看出，加載得到的揮舞彎矩在小角度范圍內與β呈線性關系。

綜上所述，可以采用該方法進行槳葉載荷校準前的預扭角確定。

2應變計改裝

某型直升機槳葉載荷測量剖面有兩個，分別為r1，r2，r為距離槳根處的距離。加裝電阻應變計前，首先確定徑向位置；其次，以實際槳葉翼型尺寸為基準，量取并確定各剖面1/4弦線位置，最終確定電阻應變計粘貼位置，選取類型適合的應變計完成組橋。

3預扭角確定實踐

以槳葉r1，r2剖面為例進行說明。

3.1測試準備工作

試驗采用的測試設備為CAM500系列專用應變采集器，通道激勵電壓為10V，各通道的直接輸出為碼值，用以模擬應變輸出量。根據具體測量位置的形變大小，可以調整各通道的模擬輸出范圍，以達到較為精確的測量結果。

試驗開始前，將被試槳葉安裝至專用工作臺上，調整至擺振方向。首先完成測試通道與測試設備的連接工作，確認信號正常。其次進行預加載，主要用于確認測試通道初始設置的輸出范圍是否合適。預加載載荷大小不超過校準載荷最大值。

3.2預扭角確定

正式試驗開始時，將槳葉調整至豎直方向-6°（方向可任意定，本次試驗規定翼型弦線在豎直方向左側為負，右側為正），觀察測試通道碼值變化情況，待槳葉靜止后，記錄該時刻碼值，豎直方向角度不變，加載端加載30kg砝碼，待槳葉靜止后，再記錄該時刻碼值，得到一組數據；按照一定步長，調整豎直方向角度至另一值，采用同樣的步驟記錄數據。最終得到試驗結果數據見表1和表2。

按照原理介紹的方法，由碼值增量和扭角擬合的結果如圖4、圖5所示。

由圖4、圖5可以看出，擬合直線的線性相關性非常好，分別為R2=0.998和R2=0.997，圖4中直線的截距2.996，即為r1剖面的擬合預扭角，圖5中直線的截距6.697即為r2剖面的擬合預扭角，與設計給出的設計預扭角進行比較，誤差精度為3%。為進一步驗證該擬合結果的準確性，分別將槳葉豎直方向的角度調整至2.996°和6.697°，在加載端進行逐次加載，加載過程中同時觀察對應剖面揮舞電橋的輸出。可以看出，在整個加載變換過程中，揮舞電橋的輸出很小，基本為0，進一步說明擬合結果的準確性。

4結論

通過上述完整的試驗過程，可以得到以下結論：首先，理論上分析了一種直升機槳葉預扭角確定的試驗方法；其次，以某型直升機槳葉為例，采用上述方法，完成了該槳葉預扭角確定的實踐工作，確認了該方法的可行性與準確性，為直升機槳葉載荷校準提供支持。