高中數(shù)學(xué)數(shù)列試題考查題型研究
■貴州省黃平縣舊州中學(xué) 吳定能
■貴州師范大學(xué)數(shù)學(xué)與科學(xué)學(xué)院 王寬明
高中數(shù)學(xué)數(shù)列試題考查題型研究
■貴州省黃平縣舊州中學(xué) 吳定能
■貴州師范大學(xué)數(shù)學(xué)與科學(xué)學(xué)院 王寬明
數(shù)列作為高中數(shù)學(xué)知識的幾大模塊之一,為數(shù)學(xué)中離散數(shù)據(jù)的研究提供了理論支撐。在高中教材中雖然只用了少量篇幅來陳述,但由于它自身的特性功能,在各種類型的考試試題中,占據(jù)了一定的比例。為了讓同學(xué)們清楚地認(rèn)識高中數(shù)列試題的考查方式,本文搜集了具有一定權(quán)威性的數(shù)列試題,從考查題型的角度來分析研究數(shù)列試題。
一、客觀題突出基礎(chǔ),重視函數(shù)性質(zhì)遷移
高考關(guān)于數(shù)列的客觀題考查,基本上就是考查考生對a1,d,n,an,q,Sn這五個量之間關(guān)系的掌握情況,主要有兩種考查方式:一是概念、公式;二是性質(zhì)。一般來說只要掌握等差(比)數(shù)列的定義、通項公式、求和公式及中項公式等,直接套用公式即可求解。若能巧用性質(zhì),可以更加快速有效地解決問題。若數(shù)列{an}的通項公式為an=k n+m(k,m為常數(shù)),是關(guān)于正整數(shù)變量n的一次表達(dá)式;或者an=k qn(k,q為常數(shù)),是關(guān)于正整數(shù)變量n的指數(shù)表達(dá)式。求數(shù)列{an}的前n項和,我們很快可以選用公式法求解。
性質(zhì):若{an}是等差(比)數(shù)列,且m+ n=p+q,則有am+an=aq+ap(am·an= ap·aq)。
特別地,若m+n=2k,則有am+an= 2ak(am·an=a2k)。
考慮到數(shù)列是一種特殊的函數(shù),對于客觀題而言,可以適當(dāng)根據(jù)函數(shù)的特點進(jìn)行靈活運(yùn)用。
等差數(shù)列{an}的前n項和為Sn,若a1=2,S11=1 3 2,則a6=____。
解析:因為可得a1+a11=2 4。又{an}是等差數(shù)列,所以2a6=a1+a11=2 4,可得a6=1 2。
在等差數(shù)列{an}中,已知a3+ a8=1 0,則3a5+a7=____。
解析:因為a3+a8=1 0,所以a5+a6= 1 0。所以3a5+a7=2a5+(a5+a7)=2a5+ 2a6=2(a5+a6)=2 0。
其實,數(shù)列的函數(shù)性質(zhì),在習(xí)題中可以充分挖掘出來,進(jìn)而迅速、直觀地解決問題。如等差數(shù)列的前n項和Sn是經(jīng)過原點的二次函數(shù),其具有對稱性。實踐中,可利用其對稱軸解題。
二、主觀題突出運(yùn)算,重視典型解法積累
通項公式是數(shù)列的最基本的表達(dá)方式,所以與之有關(guān)的試題也就成為重點考查題型,主要考查對求解方法的掌握情況,那么涉及的方法主要有:用公式法(待定系數(shù))直接求通項公式;用累加(乘)法求數(shù)列的通項公式;由遞推關(guān)系求通項公式;由Sn與an的關(guān)系求通項公式;用猜想歸納證明的方法來求通項公式等。
1.累加法。
累加法是等差數(shù)列通項公式的推導(dǎo)方法。若遞推關(guān)系為an+1-an=f(n)且f(1)+f(2)+…+f(n)是可以化為特殊數(shù)列求和的。若f(n)是常數(shù),則{an}為等差數(shù)列。
數(shù)列{an}滿足a1=1,且an+1-an=n+1(n∈N*),則數(shù)列的前1 0項和為____。
分析:依據(jù)an+1-an=f(n),先用累加法求出數(shù)列{an}的通項公式,然后根據(jù)通項公式的特點,用裂項相消法求和。
解:由題可得an-a1=(an-an-1)+ (an-1-an-2)+…+(a2-a1)=n+(n-1)+ (n-2)+…+2,所以an=n+(n-1)+可得
2.累乘法。累乘法是等比數(shù)列通項公式的推導(dǎo)方法。若且f(1)·f(2)·…·f(n)是容易求積的,可以用累乘法求數(shù)列的通項公式。
(Ⅰ)求數(shù)列{xn}的通項公式;
(Ⅱ)記Tn=x21x23…x22n-1,證明
分析:第(Ⅰ)問按照題意就可以求解,關(guān)鍵是第(Ⅱ)問,根據(jù)已知我們要證需考慮通項由通項直接求積化簡運(yùn)算,所以需要對通項進(jìn)行放縮建立不等關(guān)系。
解:(Ⅰ)過程略。
(Ⅱ)由題意結(jié)合(Ⅰ)得Tn=x21·
3.裂項相消法。
若數(shù)列{an}的通項公式能夠分裂成兩項之差,然后在求和表達(dá)式中有前后項可以相互抵消,這時候我們就用裂項相消法求和。常見的類型有:
已知{an}是各項均為正數(shù)的等差數(shù)列,公差為d,對任意的n∈N*,bn是an和an+1的等比中項。
(1)設(shè) ,求證:數(shù)列{cn} 是等差數(shù)列;
解析:(1)cn==an+1an+2-anan+1=2d·an+1,cn+1-cn=2d(an+2-an+1)=2d2為定值,所以{cn}為等差數(shù)列。
(2)Tn= =c1+c3+…+c2n-1=n c1+·4d2=n c1+2d2n(n-1)。
由已知得c1=b22-b21=a2a3-a1a2= 2d a2=2d(a1+d)=4d2,將c1=4d2代入上式得Tn=2d2n(n+1)。
4.定義法。
根據(jù)數(shù)列的定義,我們可以得到an與Sn的關(guān)系為從而求出數(shù)列{an}的通項公式,這里主要談兩種類型: (1)Sn=f(n);(2)Sn=f(an)。
設(shè)數(shù)列{an}的前n項和Sn= 2an-a1,且a1,a2+1,a3成等差數(shù)列,求數(shù)列{an}的通項公式。
分析:該題屬于Sn=f(an)型,利用an與Sn的關(guān)系消去Sn,得到an+1與an之間的遞推關(guān)系,再選擇適當(dāng)方法求解。
解:已知Sn=2an-a1,則an+1=Sn+1-Sn=2an+1-2an,所以an+1=2an,所以a2= 2a1,a3=2a2=4a1。
又a1,a2+1,a3成等差數(shù)列,所以a1+ a3=2(a2+1),即a1+4a1=2(2a1+1),解得a1=2。
所以數(shù)列{an}是首項為2,公比為2的等比數(shù)列,即an=2n。
該題主要考查由Sn與an的關(guān)系求通項公式,先根據(jù)消去Sn后剩下an與an-1之間的關(guān)系或關(guān)于n的表達(dá)式,即建立新的遞推關(guān)系進(jìn)行求解,同時應(yīng)注意討論及驗證n=1的情況。
5.錯位相減法。
設(shè)等差數(shù)列{an}的公差為d,前n項和為Sn,等比數(shù)列{bn}的公比為q。已知b1=a1,b2=2,q=d,S10=1 0 0。
(Ⅰ)求數(shù)列{an},{bn}的通項公式;
分析:依據(jù)題意,第(Ⅱ)問可用錯位相減法求數(shù)列{cn}的前n項和。
解:(Ⅰ)由題意知解得或故或
(Ⅱ)由d>1,可得an=2n-1,bn= 2n-1,即

若數(shù)列{cn}的通項公式可表示為cn= an·bn,數(shù)列{an}與{bn}分別為等差數(shù)列和等比數(shù)列,等比數(shù)列的公比為q,若求數(shù)列{cn}的前n項和Sn,首先把Sn表示出來,然后構(gòu)造q Sn等式,最后采用錯位相減法求和。
三、信息題突出推理,重視閱讀素養(yǎng)培養(yǎng)
這類題型由于情境陌生、信息量較大,同學(xué)們一般在閱讀和理解方面存在某種程度的困難。同時,這類題對信息的提取、選擇和知識的綜合運(yùn)用,以及同學(xué)們的推理能力有較高的要求。
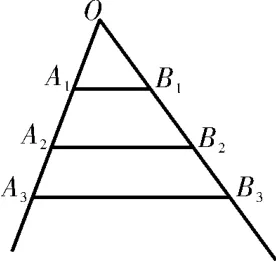
圖1
如圖1,互不相同的點A1,A2,…,An,…和B1,B2…,Bn,…分別在角O的兩條邊上,所有AnBn相互平 行,且 所 有 梯 形AnBnBn+1An+1的面積均相等。設(shè)O An=an。若a1=1,a2=2,則數(shù)列{an}的通項公式是____。
解析:設(shè)S△OA1B1=S,由已知得a1= O A1=1,a2=O A2=2,且有△O A1B1∽△O A2B2,所以所以
又所有梯形AnBnBn+1An+1的面積均相等,所以所以所以an=
近幾年的高考數(shù)列題,有些是直接考查數(shù)列知識的,有些是考查有關(guān)數(shù)列知識綜合運(yùn)用的,有些是考查數(shù)列知識遷移的,對數(shù)列知識的了解、理解和掌握等層次的要求均有涉及。實踐中,需要同學(xué)們加強(qiáng)對知識的理解,強(qiáng)調(diào)與其他內(nèi)容的融合,尤其是函數(shù)、不等式等方面的內(nèi)容,同時也需要同學(xué)們記住并且掌握典型的方法。如此,同學(xué)們方可從容面對高考,面臨信息題時,也能處變不驚,充分發(fā)揮自己解決問題的能力。
(責(zé)任編輯 王福華)

