高原環境連續下坡路段大貨車行車速度預測模型*

陳立輝 郭忠印

(同濟大學道路與交通工程教育部重點實驗室 上海 201804)

0 引 言

公路連續下坡路段是事故高發路段[1].與低海拔環境不同，針對高原環境下的連續下坡路段道路安全研究成果較少.高原環境具有典型而惡劣的氣候條件，大氣壓和含氧量隨海拔高度升高而降低，海拔高度5 000 m，大氣壓力下降約46%，大氣含氧量下降約46.7%，大氣壓力和含氧量的降低對交通安全系統會產生一系列影響，首先是對駕駛員的生心理的影響，主要包括反應時間、心率、運動系統等[2-4].其次是對車輛的影響，主要體現在車輛的動力性能和氣壓制動性能[5-6]上.車輛的實際行駛速度總是隨公路線形、車輛性能,以及駕駛員特性等各種條件的改變而改變，高原環境對車輛和駕駛員的影響最終都會通過車輛速度的形式表現出來.

為了研究高原環境連續下坡路段的車速特征，本文以214國道海拔高度4 600～4 800 m的巴顏喀拉山段連續下坡為研究對象，通過VBOX III設備采集試驗車輛的連續行車速度數據，分析縱坡參數對行車速度的影響，通過回歸分析，建立高原環境連續下坡路段的載重貨車行車速度預測模型.

1 試驗設計

從試驗的角度來看，與使用雷達設備或位于固定點的其他傳感器的定點測量不同，本研究采用GPS設備沿車輛行駛路徑連續收集速度數據，避免了斷面法定點采樣的離散型對車速行駛軌跡的破壞.以標準載重49 t的東風天龍半掛車為試驗車型，利用安裝在車頂的車載VBOX III設備的全球定位系統(GPS)，采集國道214線海拔高度4 600～4 800 m的巴顏喀拉山一段連續下坡行車速度數據.

為了防止不同駕駛習慣對試驗造成的干擾，本試驗選擇一名本地駕駛員駕駛試驗車輛，數據采集時間間隔為1 s.試驗時段選擇08:00—16:00的晴朗天氣，車流為自由流，試驗共進行了20次.

為了排除明顯不合理的數據對試驗結果產生影響，本試驗在數據選擇上進行了降噪處理，選擇坡度單一、車速穩定路段車速數據作為分析數據來源，排除因不同坡度及車速離散過大對結果造成的影響.

2 運行速度預測模型

2.1 參數選擇

影響載重貨車下坡路段的行車速度因素有很多，如坡度、坡長、車輛總重量、車輛進入縱坡的初速度、空氣阻力、駕駛員技能等.根據本研究目的，結合文獻[7-9]，選擇坡度、坡長作為自變量.

根據實測數據繪制散點圖，首先繪制坡度與速度散點圖，見圖1.根據散點圖的變化趨勢，結合多模型評估，選擇二次多項式作為擬合模型，擬合方程為

y=2.566 3x2-23.548x+76.835

R2=0.644 5

(1)

由判定系數R2=0.644 5可知，坡度與車輛運行速度二次多項式關系較為顯著.

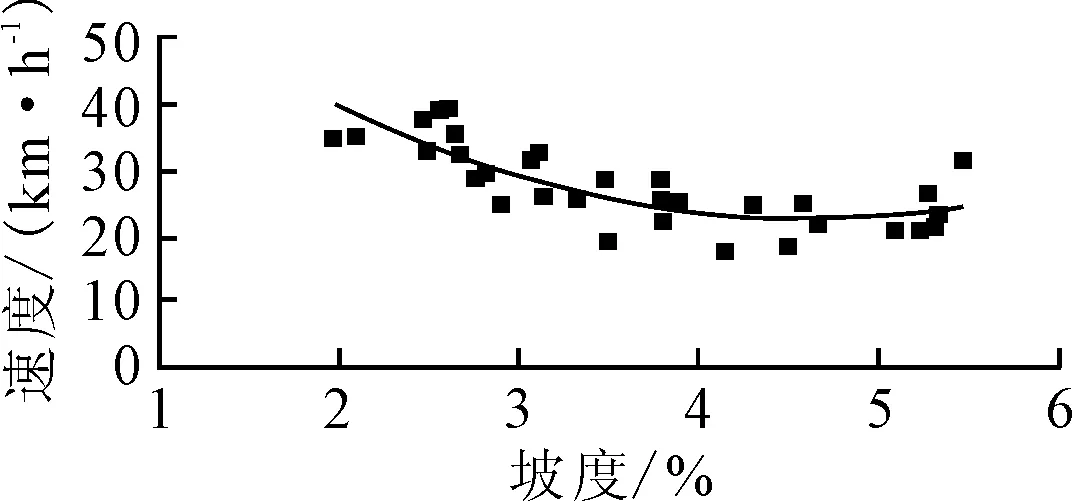
圖1 坡度與車速關系圖

其次，繪制坡長與速度散點圖，見圖2.同樣根據散點圖的變化趨勢，結合多模型評估，選擇二次多項式作為擬合模型，擬合方程為

y=-0.668 5x2+6.917x+19.167

R2=0.601 7

(2)

由判定系數R2=0.601 7可知，坡長與車輛運行速度二次多項式關系同樣較為顯著.

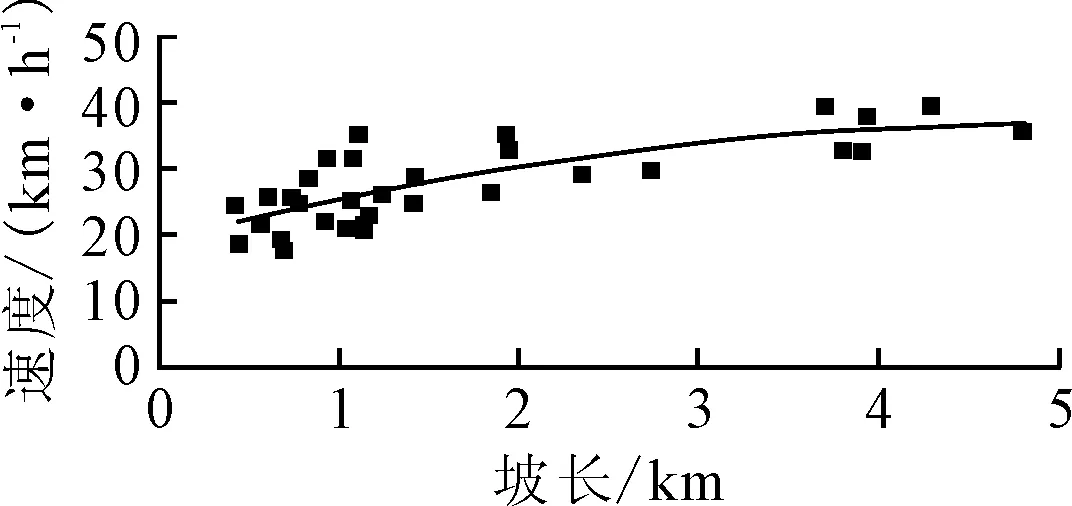
圖2 坡長與車速關系圖

2.2 模型構建

根據上述分析，選擇二元二次多項式作為擬合模型，設縱坡坡度變量P為，坡長變量L為，車速V為y，回歸模型如下為

句中“朝士善歷者”為定語后置句式，“善歷”為定語，“朝士”為中心語，“者”為定語后置的標志。翻譯時應按現代漢語的表達習慣加以調整，即“精通（擅長）歷法的朝中大臣”。

(3)

y=a0+a1x1+a2x2+a3x3+a4x4+a5x5(4)

式中：a0為常數項；ai為變量系數，i=1～5.

根據概率原理，y為隨機變量，將方程化為矩陣形式：

(5)

yn×1=xn×pap×1+εn×1

(6)

也可記為

y=X·a+ε

(7)

根據殘差平方和：

SSR=ε′ε=(y-Xa)′(y-Xa)

(8)

根據最小二乘法原理，通過對殘差平方和進行最小化，就可以得到總體參數的最小二乘估計a.

a=(X′X)-1X′y

(9)

通過經典線性回歸進行模型構建，排除雖然個別變量參數顯著性檢驗的擬合方程得到滿足，但回歸方程參數共線性始終無法消除的問題，以及膨脹因子VIF超過10的上限導致共線性嚴重，致使模型估計失真或難以估計準確，本文通過嶺回歸的方式，對多元線性回歸模型進行嶺回歸，避免上述問題的出現.

2.2.1嶺回歸原理

嶺回歸(ridge regression)是在平方誤差的基礎上增加正則項，見式(10)～(11)，其中，k為嶺參數，范圍為0～1.0.

Lossfunction=

(11)

2.2.2K值選取

本文通過方差擴大因子法選擇k值，方差擴大因子VIF度量了多重共結性的嚴重程度，一般當與VIF>10 時，模型就有嚴重的多重共線性.因此，選擇k的經驗做法是使所有方差擴大因子VIF≤10，這時所對應的k值的嶺估計就會相對穩定.

本研究基于R語言進行嶺回歸分析，圖3為嶺參數k與膨脹因子VIF的關系圖.當VIF≤10時，即可滿足回歸方程對膨脹系數的要求.由圖3可知，嶺參數k約為0.4時，膨脹因子VIF在10以內，因此，本文取嶺參數為0.4.

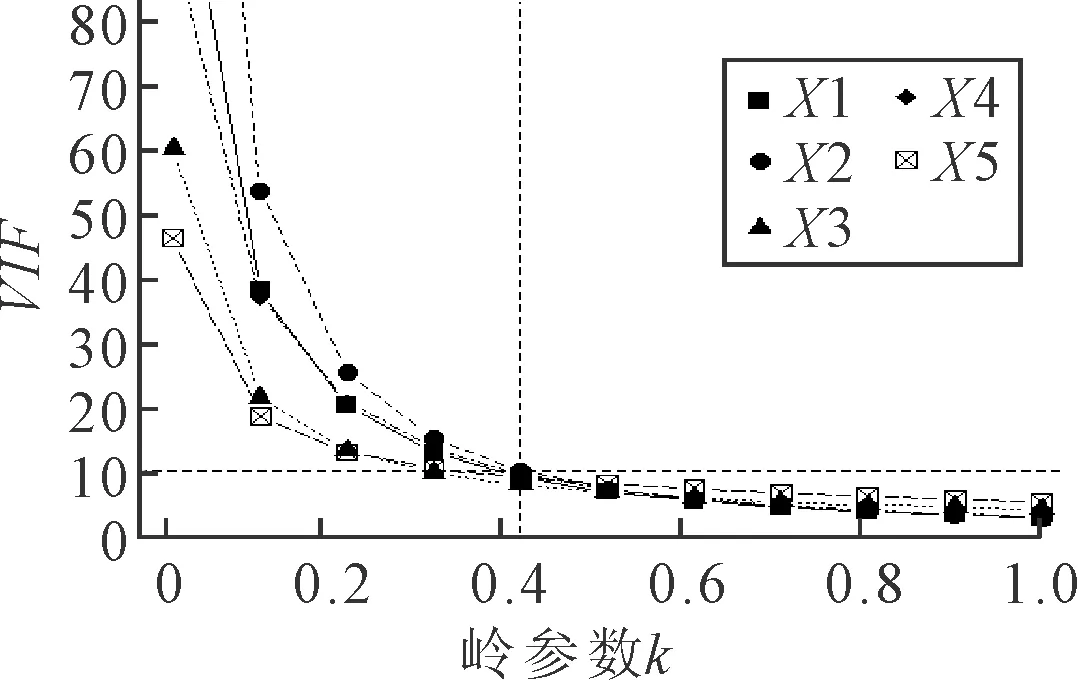
圖3 嶺參數與膨脹因子關系圖

根據選擇的嶺參數k值，可以確定具體的參數估計值，圖4為選擇不同的嶺參數值時對應的膨脹因子VIF值，圖中豎向虛線為k取0.4時，對應的回歸方程中的參數值.

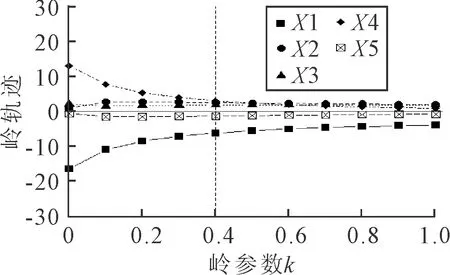
圖4 參數嶺軌跡圖

當k取0.4時，模型調整后R2=0.65，意味著自變量對因變量的解釋程度較好，可以滿足回歸分析的需要.同時根據德賓-沃森檢驗值為1.501<10，不存在顯著的自相關問題.見表1.

表1 模型摘要

根據回歸結果得到的對應參數值及相關顯著性檢驗，見表2.

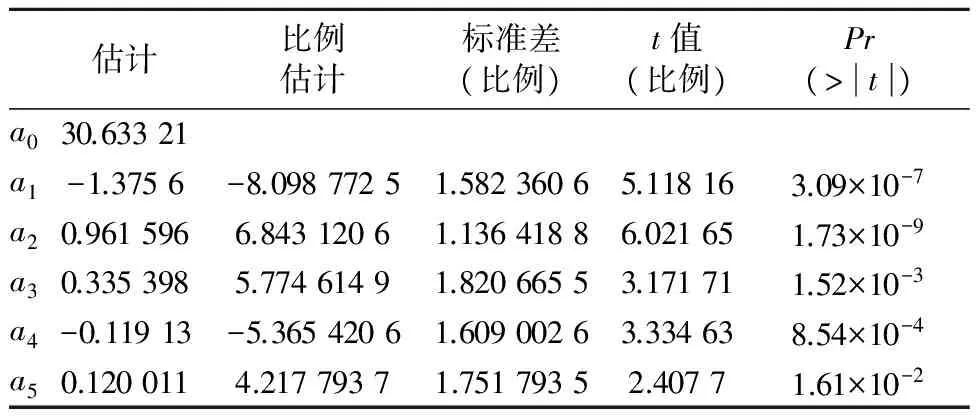
表2 回歸系數及顯著性檢驗

將得到的參數值帶入方程，最后得到的回歸方程為

y=30.633 2-1.375 6X1+0.961 6X2+

R2=0.65

(12)

將具體的變量代入方程即可得到速度與坡度、坡長的回歸方程。

V=30.633 2-1.375 6P+0.961 6L+

0.335 4PL-0.119 1P2+0.12L2

R2=0.65

(13)

3 應用實例分析

為了檢驗回歸模型的適用性及準確性，對原有路段又進行了四次試驗，根據不同的坡度及坡長，從四次試驗中選擇15段縱坡，統計每段縱坡的坡度、坡長和采集到的速度值，將坡度、坡長數據帶入得到的行車速度預測模型回，通過實測數據與預測數據對比，驗證回歸模型的有效性，具體對比見圖5.

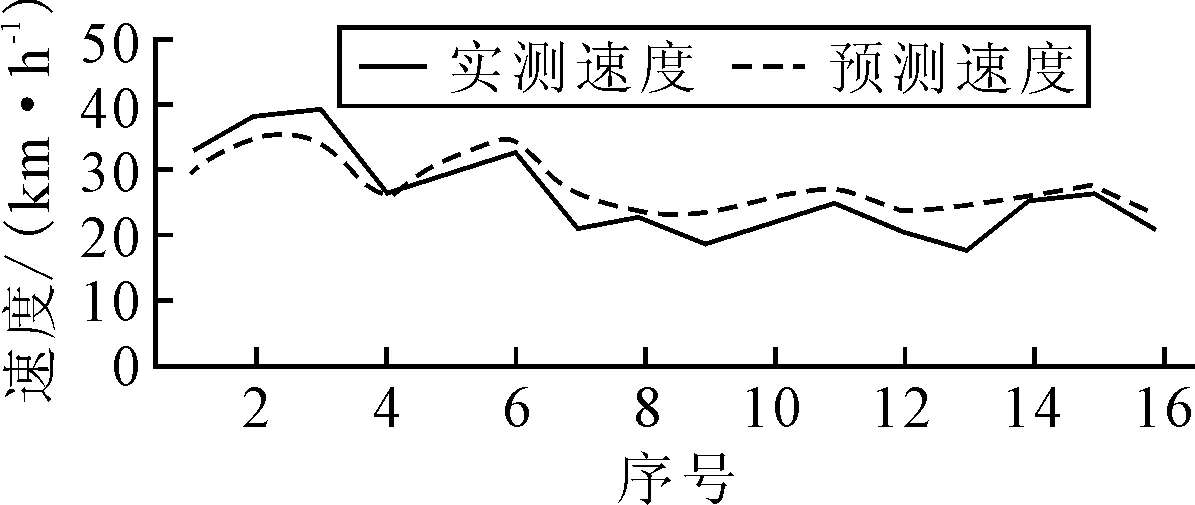
圖5 預測車速與實測車速比較圖

由圖5可知，預測值基本能夠反映實測值的趨勢，根據數據統計，回歸模型平均誤差約為7.45%，在可以接受范圍.

4 結 束 語

斷面法基于斷面上大量車輛行車速度的統計學分析，因受斷面數量的限制，很難精確描述車輛的實時速度狀態特征，基于GPS的連續觀測法，可以采集車輛行駛方向上連續的行車速度數據，更加精確的描述行車速度與縱斷面參數之間的彌補斷面法縱向行車速度的缺點，只要數據量夠大，則可以兼顧斷面法優點的同時，精確統計縱坡路段上車輛的準確狀態特征.

從多變量回歸的變量選擇來說，普通的多元線性回歸要做的是變量的剔除和篩選，而嶺回歸是一種收縮的方法，而不是刪除該變量.嶺回歸是對最小二乘回歸的一種補充，它損失了無偏性，來換取高的數值穩定性，從而得到較高的計算精度，針對共線性問題，是個比較好的方法.

高原環境連續下坡路段的行車速度研究成果較少，本文通過實車試驗，大樣本量行車速度數據回歸海拔4 600～4 800 m的連續下坡路段運行速度預測模型，為高原環境連續下坡路段的設計和安全研究提供了理論基礎.本文因試驗條件所限，無法兼顧不同載重條件下的車輛試驗，需要在進一步的研究中給出修正.

[1] AASHTO A. Policy on geometric design of highways and streets[J]. American Association of State Highway and Transportation Officials, Washington D C,2001(1):158-163.

[2] 葉慶華,陳林聲,胡鴻勤.駕駛員進入高原不同海拔高度的反應時改變[J].交通醫學,1993(1):14-15.

[3] 艾力·斯木吐拉,李巖巖,伊力扎提·艾力.高原公路駕駛員生理特性動態試驗分析[J].中國安全科學學報,2016,26(5):7-12.

[4] 楊國愉,馮正直,汪濤.高原缺氧對心理功能的影響及防護[J].中華行為醫學與腦科學雜志,2003,12(4):471-473.

[5] 張永虎,熊云,劉曉,等.富氧進氣改善高原汽車發動機動力性和經濟性研究[J].汽車技術,2011(3):24-27.

[6] 魏偉,王培強.高原低氣壓環境下列車制動能力預測[J].鐵道車輛,2005,43(12):8-12.

[7] 鄧云潮.公路連續下坡路段小客車運行速度預測模型[J].長安大學學報(自然科學版)，2009(4):43-47.

[8] 許金良,葉亞麗,蘇英平,等.雙車道二級公路縱坡段車輛運行速度預測模型[J].中國公路學報,2008(6):31-36.

[9] SAGARDOY R C, GALLEGO M. New approach to defining continuous speed profile models for two-lane rural roads[J]. Transportation Research Record Journal of the Transportation Research Board,2012,23(1):157-167.