智能船舶傳感器間歇性故障容錯濾波算法*

周志杰 徐海祥 馮 輝

(武漢理工大學(xué)高性能船舶技術(shù)教育部重點(diǎn)實(shí)驗(yàn)室1) 武漢 430063) (武漢理工大學(xué)交通學(xué)院2) 武漢 430063)

0 引 言

近年來，隨著船舶智能化發(fā)展，智能船舶技術(shù)領(lǐng)域激發(fā)了國內(nèi)外諸多學(xué)者強(qiáng)烈的研究興趣[1-2].智能航行應(yīng)具有在開闊水域自主航行功能，即船舶根據(jù)傳感器測量得到的自身位置信息以及周圍環(huán)境信息，通過控制算法實(shí)現(xiàn)船舶的自主航行[3].因此，智能船舶的智能化程度與自主控制精度取決于傳感器獲取的數(shù)據(jù)的精確度.然而，由于海上環(huán)境變化的不確定性，傳感器與傳感器、傳感器與其他設(shè)備之間存在相互干擾等因素，造成傳感器測量數(shù)據(jù)的失真，加上不確定性噪聲的干擾，降低了傳感器獲得的數(shù)據(jù)的可信度，甚至出現(xiàn)不可忽略的偏差.為解決不確定干擾帶來的問題，先后有多種濾波方法被設(shè)計和使用，例如均值濾波、中值濾波、滑動多項(xiàng)式濾波、α-β-γ濾波、3σ濾波、Kalman濾波、線性濾波和無跡濾波等[4].盡管在理論上可以證明上述濾波方法的可行性，然而若要應(yīng)用于工程實(shí)踐中卻往往有較大的局限性，例如Kalman濾波和無跡濾波對濾波模型精度要求較高，而實(shí)際工程中無法建立精確的濾波模型，且其不具有良好的抗干擾能力；均值濾波和中值濾波雖然無需建立濾波模型，但是這類濾波方法為平滑處理，即窗口濾波估計的結(jié)果為窗口中央的數(shù)值，而非當(dāng)前時刻下濾波處理后的傳感器數(shù)據(jù)，因此會產(chǎn)生數(shù)據(jù)延時，對于智能船舶的自主控制尤為不利；線性濾波，又稱最小二乘濾波，是基于最小二乘的思想估計出當(dāng)前時刻的數(shù)值，因此具有一定的抗干擾能力，在工程實(shí)際應(yīng)用中較為常見，然而，該方法在測量數(shù)據(jù)變化較快的情況下濾波效果較差；3σ法需要足夠數(shù)量的數(shù)據(jù)方可判斷是否為野值，這樣不僅降低了系統(tǒng)的實(shí)時性，同時增加了數(shù)據(jù)的存儲量，進(jìn)而增大了數(shù)據(jù)處理的復(fù)雜度.由于濾波器的濾波效果對數(shù)據(jù)質(zhì)量的依賴性較大，當(dāng)測量數(shù)據(jù)帶有信噪比低、有野值、隨機(jī)誤差非平穩(wěn)等情況時，傳統(tǒng)濾波器的濾波效果會受到明顯影響，甚至?xí)x測量對象真實(shí)變化情況，導(dǎo)致濾波結(jié)果失真[5-6].近年來，為解決上述問題，一方面，部分學(xué)者對傳統(tǒng)濾波器加以改進(jìn)，以增強(qiáng)其容錯性：曾靜等[7]采用四階自回歸模型進(jìn)行殘差序列的預(yù)測與故障檢測，并結(jié)合卡爾曼濾波設(shè)計出一種基于有限記憶在線預(yù)測的卡爾曼容錯濾波器；為解決GPS量測輸出信息中常含有故障信號的問題，石靜等[8]提出了一種魯棒容錯濾波算法，將GPS量測輸出中可能含有的故障信號擴(kuò)充為系統(tǒng)的狀態(tài)，通過魯棒濾波算法在線實(shí)時進(jìn)行估計，并對系統(tǒng)進(jìn)行補(bǔ)償，達(dá)到容錯的目的；耿峰等[9]提出了一種多模式聯(lián)邦高斯和粒子容錯濾波技術(shù)，以提高組合導(dǎo)航系統(tǒng)的魯棒性；Geng等[10]設(shè)計了一種帶故障檢測功能的容錯卡爾曼濾波器(fault-tolerant-kalman-filter,FTKF)，在雷達(dá)產(chǎn)生錯誤時自動檢測出故障信號并對數(shù)據(jù)進(jìn)行濾波處理，試驗(yàn)證明可以達(dá)到預(yù)期的容錯效果.另一方面，部分學(xué)者通過改變?yōu)V波器結(jié)構(gòu)增加其容錯性能：雷江濤[11]通過比較四種聯(lián)邦濾波器的結(jié)構(gòu)后指出無復(fù)位聯(lián)邦濾波模式具有良好的容錯性能；張崇猛等[12]設(shè)計了一種基于極大似然準(zhǔn)則自適應(yīng)濾波的無重置聯(lián)邦濾波器，提高了艦船導(dǎo)航系統(tǒng)的穩(wěn)定性和精度.對于智能船舶導(dǎo)航系統(tǒng)中傳感器出現(xiàn)間歇性故障的情況，大部分學(xué)者傾向于使用聯(lián)邦濾波結(jié)構(gòu)，聯(lián)邦濾波結(jié)構(gòu)雖然有比較好的容錯性能，但其對系統(tǒng)的冗余度有較高要求，并且當(dāng)較多傳感器出現(xiàn)故障時，例如智能船舶進(jìn)入強(qiáng)磁強(qiáng)電波干擾環(huán)境中致使所有電磁傳感器出現(xiàn)間歇性故障，聯(lián)邦結(jié)構(gòu)將不具備較為理想的容錯性能.在航空領(lǐng)域，胡紹林等[13]提出了一種Q濾波(Quartile Filter)算法，引入四分法取樣的基本思想，對滑動窗口中的數(shù)據(jù)進(jìn)行四分法取樣，計算四分位均值算子，并進(jìn)行殘差補(bǔ)償，這種方法雖然有較好的濾波效果，但其存在與中值濾波和均值濾波相同的延時問題，不適用于對數(shù)據(jù)實(shí)時性要求較高的智能船舶應(yīng)用之中.

本文將上述Q濾波算法引入到智能船舶應(yīng)用中，并對Q濾波算法進(jìn)行改進(jìn)，將變窗口長度、線性估計理論與Q濾波算法相結(jié)合，在保證容錯性能的同時，增強(qiáng)其實(shí)時性.

1 船舶運(yùn)動學(xué)模型建立

為便于仿真實(shí)驗(yàn)，需建立船舶運(yùn)動數(shù)學(xué)模型.船舶運(yùn)動具有6個方向的自由度：縱蕩、橫蕩、垂蕩、橫搖、縱搖和首搖.一般情況下，建立船舶平面運(yùn)動數(shù)學(xué)模型，僅考慮縱蕩、橫蕩和首搖3個自由度即可.圖1為船舶平面運(yùn)動坐標(biāo)系.

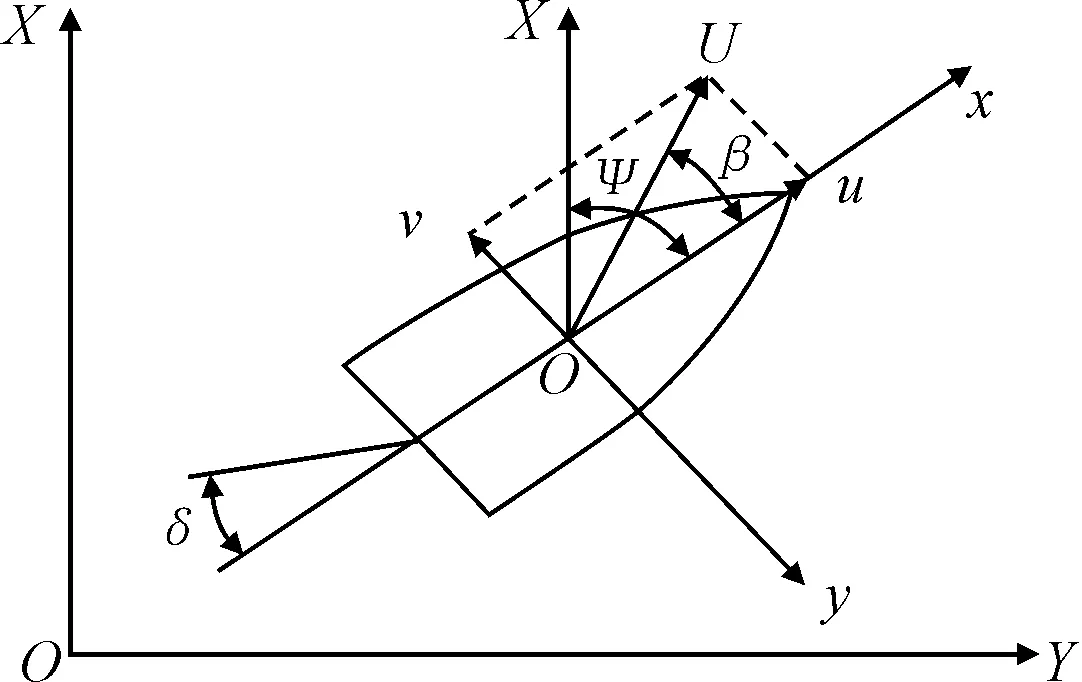
圖1 船舶運(yùn)動坐標(biāo)系

圖中：XOY為大地坐標(biāo)系；xoy為隨船坐標(biāo)系.

設(shè)船舶受外界小擾動時，縱向速度不變，其運(yùn)動方程為

(1)

(2)

式中：m為船體質(zhì)量；my，mx為船體附加質(zhì)量；u0為橫向速度；ω為首向速度；Izz為繞Z軸的轉(zhuǎn)動慣量；Jzz為船體附加慣性矩；δ為舵角；Yv，Yr，Yδ，Nv，Nr，Nδ為水動力導(dǎo)數(shù).

對于水面船舶的操縱運(yùn)動，我們最關(guān)心的是首向角Ψ和角速度ω隨時間變化的規(guī)律，即二階操縱運(yùn)動方程為

(3)

式中：

(NrYv+Nv(mU-Yr))

(NrYv+Nv(mU-Yr))

K=(YδNv-NδYv)/(NrYv+Nv(mU-Yr))

其中：U為船舶縱向速度.

對于一般船舶，由于操舵速度有限，且船舶本身的慣性很大，對舵的響應(yīng)基本上是一種緩慢的運(yùn)動，所以上式可以近似寫為一階形式，即

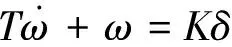
(4)

式(4)即為K-T方程.選取上述方程作為算法仿真研究采用的船舶運(yùn)動學(xué)模型，其中K，T系數(shù)根據(jù)具體船舶的操縱性能指數(shù)而定.

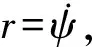
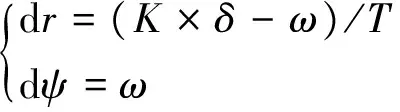
(5)

通過解微分方程組(5)，可得到運(yùn)動角速度隨時間變化的函數(shù)，即可用于推算船舶運(yùn)動位置信息.

2 容錯濾波算法設(shè)計

對于傳感器動態(tài)測量的數(shù)據(jù)，可以將其“加性”分解，即

y(tk)=s(tk)+ε(tk)+σ(tk)

(6)

式中：y(tk)為傳感器測量的數(shù)據(jù)值；s(tk)為絕對真值；ε(tk)為噪聲干擾項(xiàng)；σ(tk)為隨機(jī)野值.由上式可知，傳感器測量得到的數(shù)據(jù)與絕對真值存在兩項(xiàng)誤差：具有恒定均值的噪聲項(xiàng)與具有極大不確定性的野值項(xiàng).理論上，只要剔除野值并濾除噪聲項(xiàng)即可使傳感器測量得到的數(shù)據(jù)無限趨近于真值，然而困難的是如何診斷一個數(shù)據(jù)是否為野值.由于野值的產(chǎn)生源于傳感器的間接性故障如丟包、暫時性卡死等，故而野值的大小一般明顯偏離噪聲值.根據(jù)這一特點(diǎn)，可以采用四分法取樣的基本思想，去除偏大和偏小的數(shù)據(jù)，取中值附近的50%的數(shù)據(jù)為可信度較高的不帶野值的數(shù)據(jù)序列.

在航空領(lǐng)域，胡邵林等基于上述思想提出一種針對動態(tài)測量數(shù)據(jù)的Q容錯濾波算法，算法流程為

1) 選擇適當(dāng)?shù)拇皩挵霃紿的滑動時間窗口[tk-H,tk+H]內(nèi)的測量數(shù)據(jù)片段Sk={y(tk),tk∈[tk-H,tk+H]}進(jìn)行四分位均值算子的計算：

(7)

式中：nk為數(shù)據(jù)片段Sk的數(shù)據(jù)點(diǎn)個數(shù)；Q(Sk，nk)為四分位均值算子，即將獲得的數(shù)據(jù)序列Sk進(jìn)行從小到大排序，取中值左右各25%nk的數(shù)據(jù)序列計算其均值.

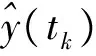
3) 將殘差序列ε(tk)進(jìn)行四分位濾波

(8)

4) 將兩次四分位濾波的結(jié)果進(jìn)行線性組合，獲得tk時刻的估計值

(9)

以上過程為Q濾波算法，雖然上述算法具有一定的容錯性，但由于該算法用于對測量數(shù)據(jù)進(jìn)行平滑處理，由1)可知，該算法的濾波對象為以某一個時刻的數(shù)據(jù)y(tk)為中心的數(shù)據(jù)片段，然而在實(shí)際應(yīng)用中，傳感器無法獲取當(dāng)前時刻tk之后的數(shù)據(jù)，因此無法根據(jù)上述算法獲得當(dāng)前時刻數(shù)據(jù)的估計值.如果將窗口前移半個窗口的長度，則Q濾波算法得到的為tk-H/2時刻的數(shù)據(jù)，若將其當(dāng)作當(dāng)前時刻的數(shù)據(jù)，將會導(dǎo)致數(shù)據(jù)延時，降低濾波算法的實(shí)時性.

針對上述問題，對Q濾波算法進(jìn)行改進(jìn)，改進(jìn)后的算法流程為

1) 選擇合適的初始滑動窗口長度ζ，取一段測量數(shù)據(jù)序列S(tk).

S(tk)={y(tk-ζ+1),y(tk-ζ+2),…,y(tk)}

(10)

2) 將獲得的數(shù)據(jù)序列進(jìn)行從小到大排序，取中值左右各25%ζ的數(shù)據(jù)序列計算其均值Q(tk).

3) 計算序列S(tk)各項(xiàng)與均值的偏差，獲得殘差序列ε(tk).

ε(tk)={y(tk-ζ+1)-Q(tk),

y(tk-ζ+2)-Q(tk)，…，y(tk)-Q(tk)} (11)

4) 將殘差序列重復(fù)過程2)，計算殘差均值，作為殘差補(bǔ)償P(tk).

5) 將2)計算的均值與殘差補(bǔ)償相加，作為參考值.

(12)

其中：

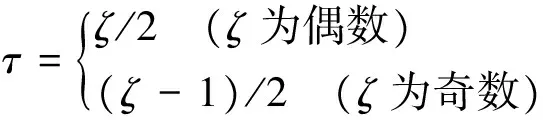
6) 取后半部分長度為τ的數(shù)據(jù)段η(tk)，重復(fù)過程2)至5)，求得后半段參考值.

η(tk)={y(tk-τ+1),y(tk-τ+2),…,y(tk)}

(13)

其中：

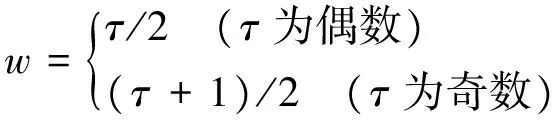
7) 通過求得的兩個參考值線性估計出y(tk)的估計值s(tk).

s(tk)=y(tk-τ)+(y(tk-w)-y(tk-τ))/

(τ-w)×τ×CS

(14)

式中：CS為修正系數(shù)，其大小與選取的初始窗口長度和數(shù)據(jù)變化率相關(guān)，通常情況下取CS的值為1.

改進(jìn)的算法在原Q濾波算法的基礎(chǔ)上，將窗口前移了半個窗口長度，并對窗口后半段數(shù)據(jù)再一次進(jìn)行了Q濾波計算，并通過線性估計的方法求得當(dāng)前時刻的數(shù)據(jù)y(tk)的估計值.

在濾波精度、克服數(shù)據(jù)遲滯效應(yīng)及實(shí)時性等方面，改進(jìn)的Q濾波算法較原Q濾波算法均有所提升：

1) 在濾波精度方面，由于原Q濾波算法主要用于數(shù)據(jù)的平滑處理，因此僅需通過篩選出置信度較高的數(shù)據(jù)片段獲取可以表征數(shù)據(jù)變化情況的數(shù)即可；而改進(jìn)的Q濾波算法在原Q濾波算法的基礎(chǔ)上，通過對窗口后半段數(shù)據(jù)進(jìn)行估值，獲取窗口數(shù)據(jù)的變化趨勢，以期估計當(dāng)前時刻的數(shù)據(jù).因此，改進(jìn)的Q濾波算法具有更高的濾波精度.

2) 在克服數(shù)據(jù)遲滯方面，原Q濾波算法主要用來估計出窗口中央的數(shù)值，即在tk時刻原Q濾波算法獲取的為tk-ζ/2(ζ為濾波窗口長度，下同)時刻的數(shù)據(jù)的濾波值，從而達(dá)到數(shù)據(jù)平滑的目的.如果將其直接應(yīng)用于對當(dāng)前時刻的數(shù)值進(jìn)行估計，則必定會產(chǎn)生遲滯效應(yīng).而改進(jìn)的Q濾波算法可以通過獲取窗口數(shù)據(jù)的變化趨勢，獲取tk時刻的濾波值.因此改進(jìn)的Q濾波算法有效克服了數(shù)據(jù)的估計延遲問題.

3) 在實(shí)時性方面，原Q濾波算法為估計出當(dāng)前時刻的濾波值，需要通過滑動窗口進(jìn)行ζ/2次四分位均值算子的計算；而改進(jìn)的Q濾波算法僅需進(jìn)行兩次四分位均值算子得計算即可獲取當(dāng)前時刻的濾波值.當(dāng)窗口長度越長，原Q濾波算法耗時越長，而改進(jìn)的Q濾波算法的耗時幾乎不發(fā)生變化.因此，改進(jìn)Q濾波算法有更好的實(shí)時性.

綜合上述，該算法不僅保留了原Q濾波算法的容錯性能，而且在濾波精度、克服遲滯效應(yīng)及實(shí)時性等方面均較原Q濾波算法優(yōu)良.

3 實(shí)驗(yàn)仿真與結(jié)果分析

為驗(yàn)證本文提出的改進(jìn)算法的可行性，本文分別對智能船舶低速直航和低速回轉(zhuǎn)運(yùn)動下傳感器獲取的信息進(jìn)行處理，并與原Q濾波算法和目前實(shí)際工程中應(yīng)用較為廣泛的線性擬合濾波方法進(jìn)行對比.

仿真實(shí)驗(yàn)基于MATLAB平臺.仿真中采用文獻(xiàn)[14]中的無人艇作為仿真對象，選取0.14 m吃水、1.2 kn航速、15°舵角時的K，T指數(shù)作為本文仿真采用的參數(shù)，即K=1.1，T=0.17.

3.1 直航工況下的仿真對比

假定船舶從原點(diǎn)出發(fā)，以1 m/s的航速沿60°方向直線航行.在不存在任何噪聲干擾情況下，船舶理想運(yùn)動情況見圖2.

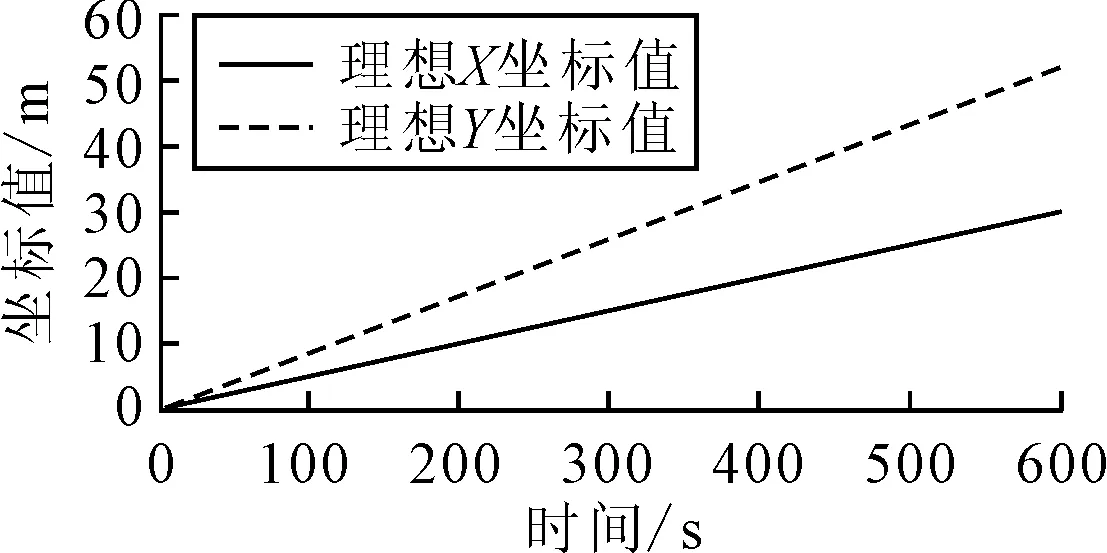
圖2 理想情況下船舶位置測量值

真實(shí)情況下，傳感器測量帶有一定的量測噪聲，且當(dāng)傳感器發(fā)生間歇性故障時，帶有故障信息見圖3.

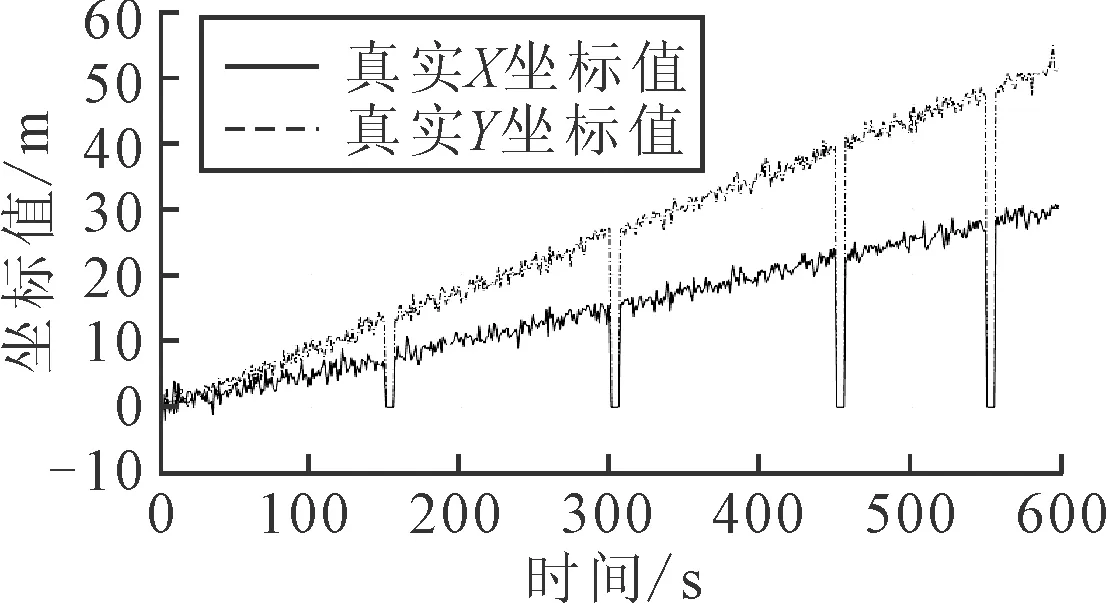
圖3 帶故障信息的傳感器測量數(shù)據(jù)

由圖3可知，最常見的傳感器間歇性故障為傳感器間歇性丟包.假定傳感器在隨機(jī)四個時刻傳感器出現(xiàn)丟包現(xiàn)象，即獲取到的數(shù)據(jù)為0.針對這種情形，分別采用三種濾波算法進(jìn)行濾波處理，并將三種算法得到的結(jié)果與理想情況下的測量值進(jìn)行對比，見圖4.

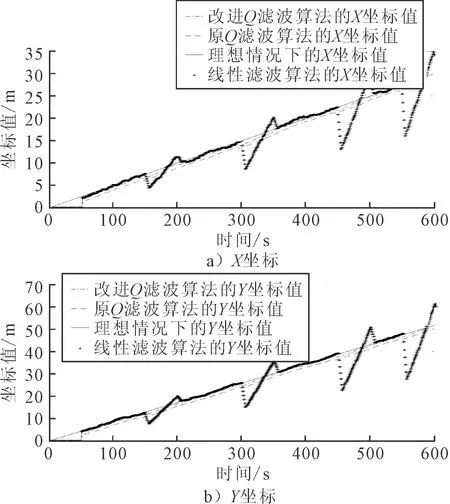
圖4 3種算法濾波結(jié)果對比

由圖4可知，線性濾波算法的容錯性能較差；而原Q濾波算法雖然有較好的容錯性能，然而存在數(shù)據(jù)延時的現(xiàn)象；改進(jìn)Q濾波算法與理想情況下的測量值最為貼近.因此綜合容錯性能和濾波效果兩個方面，改進(jìn)Q濾波算法較其他兩種算法更為理想.

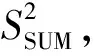
表1 傳感器間歇性故障下三種濾波算法的評估指標(biāo)對比

由表1可知，改進(jìn)Q容錯濾波算法在傳感器發(fā)生間歇性故障情況下的3個評價指標(biāo)相比于其他兩種濾波算法均有較大幅度的減小，即在船舶直航工況下，改進(jìn)Q容錯濾波算法具有更良好的濾波性能及容錯性能.

在算法耗時方面，采用原Q濾波算法和改進(jìn)的Q濾波算法對長度為600的數(shù)據(jù)進(jìn)行濾波處理，原Q濾波算法耗時約0.387 5 s，改進(jìn)的Q濾波算法耗時僅約0.073 4 s.因此，改進(jìn)的Q濾波算法與原Q濾波算法相比具有更好的快速性.

3.2 回轉(zhuǎn)運(yùn)動工況下的仿真對比

假定船舶以15°舵角做定常回轉(zhuǎn)運(yùn)動，圖5a)為理想狀態(tài)下船舶回轉(zhuǎn)運(yùn)動時大地坐標(biāo)系下X，Y坐標(biāo)值的變化曲線；圖5b)為理想的船舶回轉(zhuǎn)運(yùn)動軌跡圖.

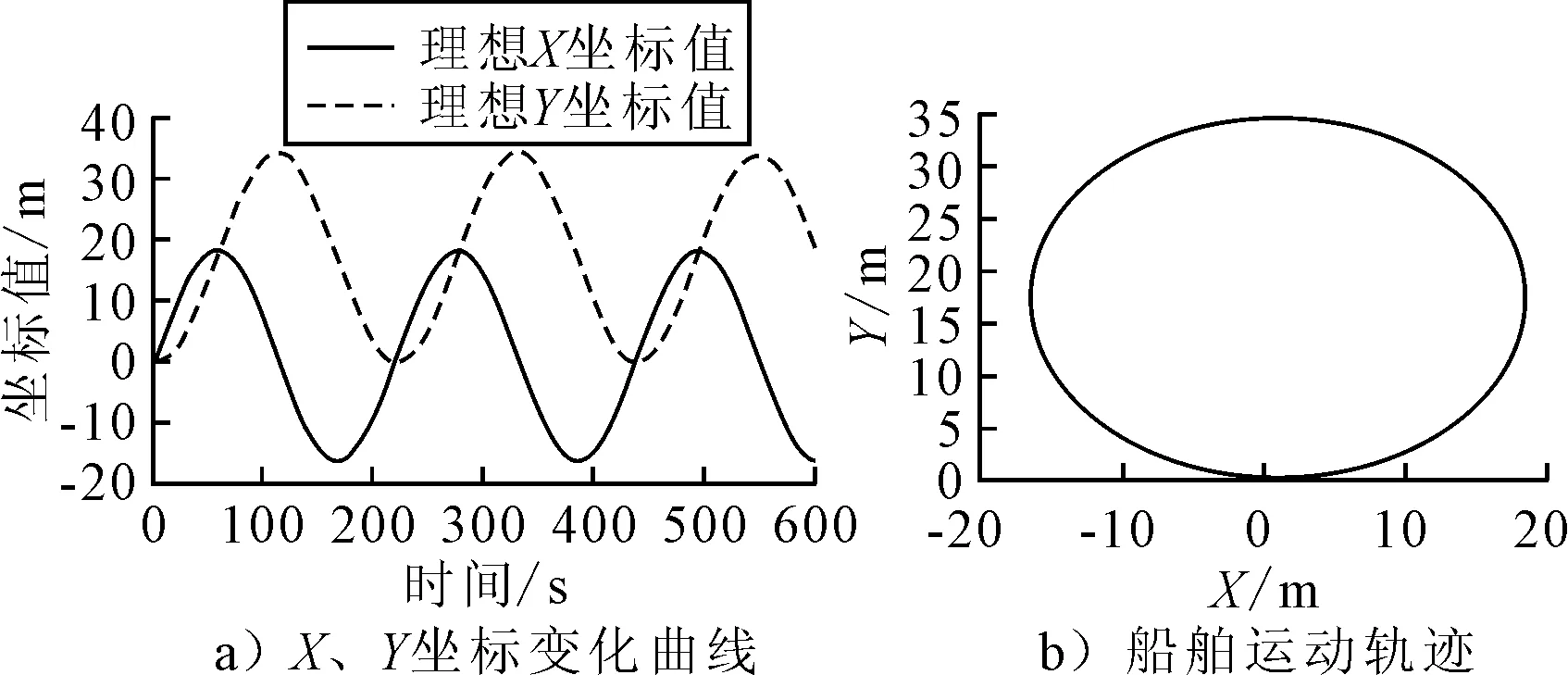
圖5 理想情況下的船舶回轉(zhuǎn)運(yùn)動位置測量值

由圖5可知，當(dāng)不存在噪聲干擾及測量野值存在時，測量值可以近乎認(rèn)為是真值.然而實(shí)際應(yīng)用中，由于船舶在隨機(jī)的環(huán)境中航行，加上船用設(shè)備對傳感器的干擾，必然存在噪聲項(xiàng)與測量野值，甚至?xí)霈F(xiàn)傳感器間歇性故障(測量數(shù)據(jù)歸零).圖6為添加了均值為0，方差為2的高斯白噪聲的測量數(shù)據(jù)，并假設(shè)在四個時間點(diǎn)傳感器出現(xiàn)了間歇性故障.

由圖6可知，添加了噪聲項(xiàng)后，測量數(shù)據(jù)出現(xiàn)上下的波動，假定在隨機(jī)四個時刻傳感器出現(xiàn)丟包現(xiàn)象，數(shù)據(jù)為0.分別采用改進(jìn)的Q容錯濾波算法、原Q濾波算法和線性濾波算法，對真實(shí)數(shù)據(jù)進(jìn)行濾波處理，并將濾波后的數(shù)據(jù)與理想情況下的測量值對比.圖7a)為X坐標(biāo)值的濾波結(jié)果；圖7b)為Y坐標(biāo)值的濾波結(jié)果.

圖6 真實(shí)情況下的測量數(shù)據(jù)

圖7 3種濾波算法結(jié)果對比

由圖7可知，線性濾波算法在故障時刻附近數(shù)據(jù)發(fā)生跳變，故而容錯性能較差；原Q濾波算法雖然有較好的容錯性能，然而相比于理想情況下的測量值總有一段時間的滯后，因此實(shí)時性較差；改進(jìn)的Q濾波算法與理想情況下的測量值最為吻合.因此相比于其他兩種濾波算法，改進(jìn)的Q濾波算法無論是在濾波效果還是容錯性能方面均較為理想.

表2為采用平滑度指標(biāo)對三種算法進(jìn)行評估的結(jié)果，計算區(qū)間取t為100～500 s.

表2 傳感器間歇性故障下三種濾波算法的評估指標(biāo)對比

由表2可知，改進(jìn)Q容錯濾波算法在傳感器發(fā)生間歇性故障情況下的各項(xiàng)評估指標(biāo)相比于其他兩種濾波算法均有較大幅度的減小，即在船舶回轉(zhuǎn)運(yùn)動工況下，改進(jìn)Q容錯濾波算法具有更良好的濾波性能及容錯性能.

采用原Q濾波算法和改進(jìn)的Q濾波算法對長度為600的數(shù)據(jù)進(jìn)行濾波處理，原Q濾波算法耗時約0.362 1 s，改進(jìn)的Q濾波算法耗時僅約0.051 9 s.因此，進(jìn)一步驗(yàn)證了改進(jìn)的Q濾波算法與原Q濾波算法相比具有更好的快速性.

4 模型試驗(yàn)驗(yàn)證

試驗(yàn)采用高精度定位傳感器，可認(rèn)為設(shè)定基站以設(shè)定坐標(biāo)系.試驗(yàn)設(shè)定固定點(diǎn)坐標(biāo)為(0，0)，截取試驗(yàn)過程中采集的某段控制周期內(nèi)的位置信息分別繪制X，Y隨控制周期的變化曲線，并分別采用原Q濾波算法和改進(jìn)的Q濾波算法進(jìn)行濾波處理.圖8a)為X坐標(biāo)隨控制周期的變化曲線，圖8b)為Y坐標(biāo)隨控制周期的變化曲線.

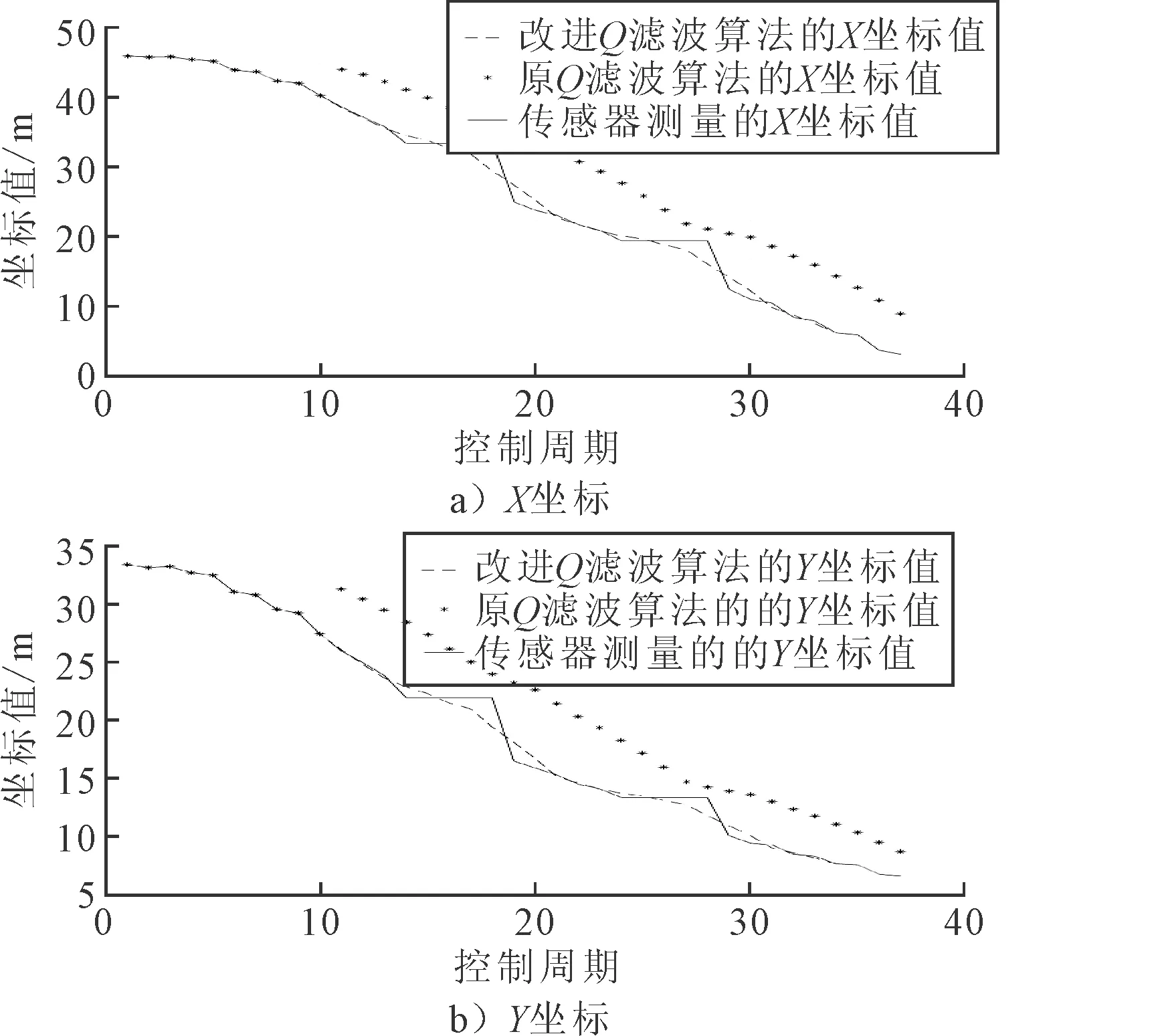
圖8 X，Y方向坐標(biāo)值隨控制周期變化曲線

由于試驗(yàn)采用的定位模塊自帶濾除高頻信號的功能，故而可以近似的認(rèn)為噪聲項(xiàng)非常小.由圖8可知，定位傳感器在第14個控制周期和第24個控制周期附近出現(xiàn)間歇性故障，由于試驗(yàn)系統(tǒng)采用數(shù)據(jù)存儲然后使用的方式，故而傳感器的間歇性故障表現(xiàn)為數(shù)據(jù)未刷新，即未采集到傳感器的數(shù)據(jù).從第10個控制周期開始采用兩種算法進(jìn)行濾波.由于原Q濾波算法的濾波值是窗口中間時刻的數(shù)據(jù)，即在第10個控制周期獲得的數(shù)值為第5個控制周期的濾波值，因此在圖9為出現(xiàn)跳變，且在第10個控制周期后，原Q濾波算法的數(shù)據(jù)存在延時滯后的現(xiàn)象，進(jìn)一步驗(yàn)證了原Q濾波算法存在實(shí)時性的不足；相比而言，改進(jìn)的Q濾波算法不僅具有良好的容錯性能和濾波效果，而且濾波得到的數(shù)據(jù)的實(shí)時性更佳.

當(dāng)傳感器出現(xiàn)間歇性故障時，會導(dǎo)致無法獲取智能船舶的位置等信息，雖然暫時性的丟包可能不會影響到最終繪制的軌跡，但是會直接影響到智能船舶的控制.例如本實(shí)驗(yàn)中出現(xiàn)丟包，系統(tǒng)讀取不到當(dāng)前時刻的信息，只能以上一時刻的數(shù)據(jù)作為控制器的輸入，這樣會導(dǎo)致控制器“致盲”，嚴(yán)重時可能會導(dǎo)致智能船舶發(fā)生碰撞等事故.由圖9可知，當(dāng)采用容錯濾波算法后，盡管傳感器無法獲取船舶的位置參數(shù)，但是濾波器可以根據(jù)以往的數(shù)據(jù)及其變化趨勢估計出該時刻的數(shù)值.

5 結(jié) 束 語

智能船舶自主控制的精度取決于傳感器測量數(shù)據(jù)的準(zhǔn)確度.然而諸多因素影響了傳感器測量數(shù)據(jù)的準(zhǔn)確度，從而降低了自主控制的精度.本文基于四分取樣具有較強(qiáng)的容錯性能這一優(yōu)點(diǎn)，設(shè)計了一種改進(jìn)的Q濾波容錯算法.數(shù)值仿真和模型試驗(yàn)結(jié)果表明，針對智能船舶搭載的傳感器出現(xiàn)間歇性的短時故障，本文改進(jìn)的Q濾波算法可以估計出故障時刻可信度較高的數(shù)據(jù)，具有較強(qiáng)的容錯性能和較好的濾波效果.

[1] CAMPBELL S, NAEEM W, IRWIN G W. A review on improving the autonomy of unmanned surface vehicles through intelligent collision avoidance manoeuvres[J]. Annual Reviews in Control,2012,36(2):267-283.

[2] 李家良.水面無人艇發(fā)展與應(yīng)用[J].火力與指揮控制,2012,37(6):203-207.

[3] 賀辭.CCS《智能船舶規(guī)范》六大功能模塊要求[J].中國船檢,2016(3):84-85.

[4] EINICKE G A. Moothing,filtering and prediction:estimating the past,present and future[R].Rijeka Croatia：Intech Press,2012.

[5] YIN S, WANG G, YANG X. Robust PLS approach for KPI-related prediction and diagnosis against outliers and missing data[J]. International Journal of Systems Science,2014,45(7):1375-1382.

[6] 胡紹林,黃劉生.計算機(jī)控制系統(tǒng)容錯設(shè)計技術(shù)及應(yīng)用[M].北京：科學(xué)出版社,2010.

[7] 曾靜,周永斌,張國良,等.基于有限記憶在線預(yù)測的卡爾曼濾波突變型故障容錯設(shè)計[J].彈箭與制導(dǎo)學(xué)報,2004(4):272-275.

[8] 石靜,繆玲娟.魯棒容錯濾波算法及在MEMS_SINS/GPS中的應(yīng)用[J].北京理工大學(xué)學(xué)報,2012,32(2):146-149.

[9] 耿峰,祝小平,周洲.一種有效的組合導(dǎo)航容錯濾波技術(shù)研究[J].西北工業(yè)大學(xué)學(xué)報,2016,34(3):449-455.

[10] GENG K K, CHULIN N A. Applications of multi-height sensors data fusion and fault-tolerant kalman filter in integrated navigation system of UAV[J]. Procedia Computer Science,2017,103:231-238.

[11] 雷江濤.容錯組合導(dǎo)航系統(tǒng)中的聯(lián)邦濾波器應(yīng)用研究[J].艦船電子工程,2012,32(2):56-58.

[12] 張崇猛,王戈,舒東亮,等.自適應(yīng)濾波的艦船綜合導(dǎo)航系統(tǒng)信息融合技術(shù)[J].火力與指揮控制,2012, 37(7):39-42.

[13] 胡紹林,傅娜,郭文明.動態(tài)測量數(shù)據(jù)的高保真容錯Q-濾波算法[J].宇航學(xué)報,2016,37(1):112-117.

[14] 馬天宇,杭岑,楊松林.一種新型水面無人艇操縱性試驗(yàn)分析[J].江蘇船舶,2016 (4):6-12.