基于相似度的軟件工程中軟件成本估算問題研究①

王 楠, 余建坤

(云南財經大學 信息學院,昆明 650021)

軟件工程過程是指開發或維護軟件及其相關產品的一系列活動. 一個完整的軟件工程開發過程包括軟件概念提出、前期需求分析、軟件結構設計、軟件詳細設計、編碼過程、軟件測試過程6個過程[1]. 隨著科技的發展,軟件的系統規模也在不斷擴大,復雜程度日益加大,需求分析作為整開發過程的基礎,在軟件工程中的重要程度和地位越來越被人們所認可. 據統計、有超過半數以上的軟件工程項目存在前期需求分析不當的問題,許多項目也因此導致延期或失敗[2]. 軟件成本估算問題作為前期需求的重中之重,也越來越被人們所重視.

如何對軟件項目進行精準成本估算,一直是軟件工程和軟件項目管理中最為重要且最具挑戰問題之一.軟件成本估算是進行有效的項目計劃、跟蹤和控制的基礎. 依照合理的估計結果,不僅能夠制定切實可行的目標,還可對軟件的成本、進度與質量進行權衡,實施有效的風險管理,并為項目管理者的決策提供有力的支撐和依據. 不準確的估計則會造成軟件工程項目的延期、超支甚至項目失敗,嚴重的還會損害企業的商業形象和信譽.

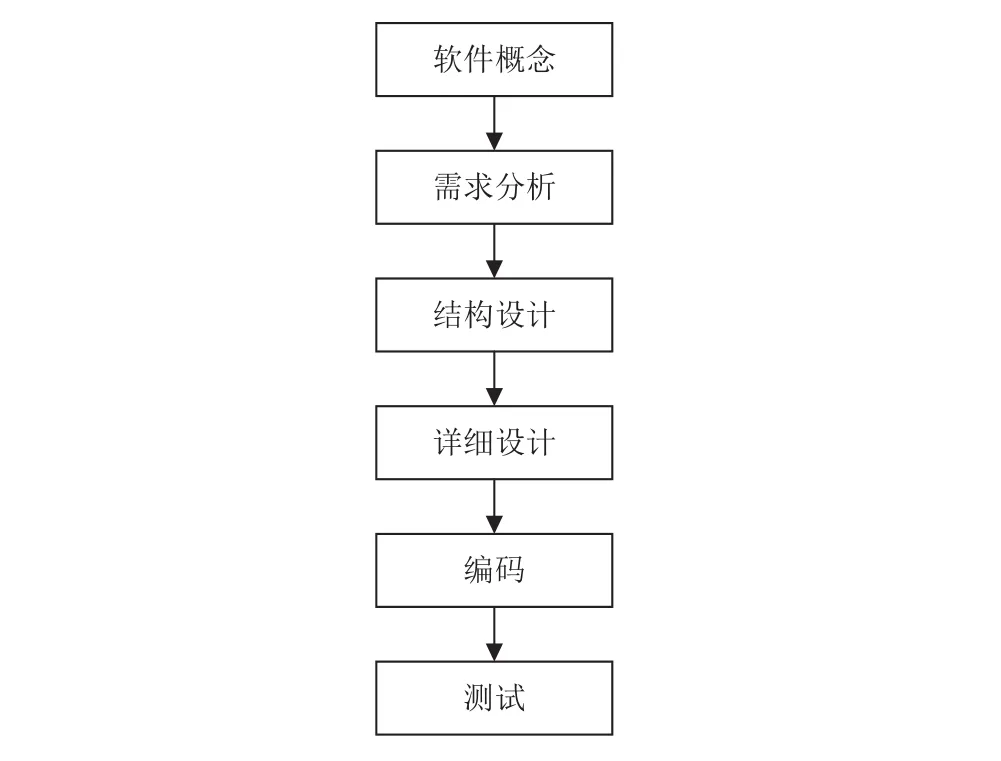
圖1 軟件工程流程

Standish組織在 1995 年公布的軟件工程報告顯示,在來自國際上350個組織的 8000個軟件工程項目中,只有16.2%項目被定義為“Succeeded”,即該項目在預算和預期內完成; 31.1%的項目被定義為“Falied”,即該項目未能按時完成或者被取消; 剩下的52.7%被定義為“Challenged”,即雖然該項目被完成,但預算超出或者項目完成不達標[3]. 2004 年,Standish組織的再次公布其統計數據,統計項目數累計超過50000多個,根據其公布的結果顯示,“Succeeded”項目所占比例為29%,“Falied”項目所占比例為 29%,有所下降,而“Challenged”項目比例仍有53%[4].

雖然有許多學者和專家認為在Standish組織公布的報告中關于軟件成本預算超支89%的數據被過分夸大,但有一點卻能夠取得共識,即不精準的軟件成本估算與需求不穩定并列,是造成軟件工程項目失敗和超期的最主要的的兩大因素.

軟件成本估算和方法和理論有很多種類和形式,最早的軟件成本估算是上 60 年代提出的SDC (System Development Corporation)方法,一直到如今,關于軟件成本度量方法主要有兩種方法：① 基于模型的軟件成本估算方法; ② 基于類比估算軟件成本估算方法[5].

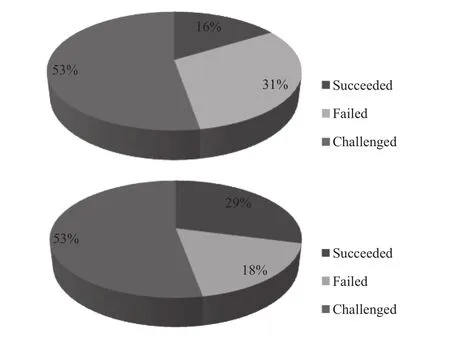
圖2 Standish組織統計數據

基于模型的軟件成本估算方法是通過將影響軟件工程項目的相關因素如項目復雜性、相關管理經驗、團隊經驗等與軟件項目的相關指標例如工作量、工作環境、工作時長等之間存在著可用公式表示的確定關系,并判定它對工作量所產生影響的程度,再從參數得到成本估算的一系列規則、公式. 以期得到最佳的模型算法表達形式,然而基于模型的軟件成本估算方法難以用在沒有前例的場合,并且不能處理異常情況等的問題. 而且算法復雜度往往比較高,所以基于模型的軟件成本估算方法存在一定缺陷[6].

基于類比的方法是是采用基于相似性度量的方法進行軟件成本的估算. 即通過對一個或多個已完成的軟件工程項目項目與新的項目之間的對比來預測當前項目的成本與進度. 在軟件成本估算中,需要當前問題抽象為待估算的項目時,每個實例即指已完成的軟件項目,通過案例識別、案例檢索以及案例適配3個步驟進行軟件實例之間成本相似性估算. 在軟件成本估算問題上,經常采用的相似性度量方法有歐式距離、熵度量、模糊度量等,例如文獻[7]提出一種基于基于協同過濾方法的軟件成本度量方法,通過用戶評分來定義屬性權重,然而這種方法依然是一種基于專家評論的方法,然而軟件工程十分復雜,單一的專家定義權重精確度并不高,用戶的個人偏好、經驗差異與專業局限性都可能為估算的準確性帶來風險,文獻[8]提出一種基于相似度的軟件成本度量方法,根據不同屬性的類型采用不同的度量公式,例如歐式距離,余弦公式等,然而這種方法依然是采用單一的度量公式來度量軟件成本相似性,而且單一的采用歐式距離等公式在軟件成本度量方面精度比較低. 文獻[9]借鑒改進了Sheperd等人關于類比估算的方法,提出來采用提取相似項目、決定最相似的項目等4個步驟來進行軟件成本相似性度量,并根據不同的屬性類別選用不同相似性度量方法,然而其依然是采用單一的度量公式進行軟件成本相似性度量、并沒有考慮如何使度量最優化的問題,其方法精確度并不高[10].

本文采用類比估算方法,提出一種采用皮爾遜相關系數的度量方法,并結合TOPSIS決策方法,采用專家評估和客觀權重綜合的方法,提出一種的基于皮爾遜相關系數的軟件成本相似性度量方法,來進行軟件成本的相似性估算,通過并通過Desharnais數據集進行了實驗驗證,證明本方法在軟件成本估算問題上相對歐式距離和其他方法在檢測精度上具有一定優勢.

1 理論背景

1.1 相關系數

相關系數(Correlation Coefficient)又稱皮爾遜相關系數. 是由著名英國數學家卡爾·皮爾遜于首次提出的一個統計學指標. 相關系數是用于反映所求變量之間相關關系密切程度的統計指標. 相關系數是按積差方法計算,同樣以兩變量與各自平均值的離差為基礎,通過兩個離差相乘來反映兩變量之間相關程度. 皮爾遜相關系數并不是唯一的相關系數,但是卻是最常見的相關系數. 皮爾遜相關關系是一種非確定性的關系,它是用來描述變量之間線性相關程度的量.

定義1. 假設存在隨機變量X,Y是兩個隨機分布,為X,Y的期望,則X與Y的協方差Cov(X,Y)被定義為：

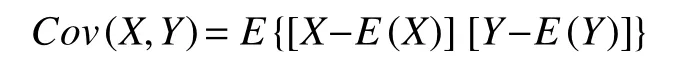
定義2. 相關系數 ρxy為：

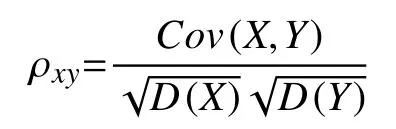
相關系數 ρxy取值在-1到1之間,ρxy=0時,稱X,Y不相關;時,稱X,Y完全相關,此時,X,Y之間具有線性函數關系;時,X的變動引起Y的部分變動,的值越大,X的變動引起Y的變動就越大,時稱為高度相關,當時稱為低度相關,其它時候為中度相關.

1.2 TOPSIS

最優劣解距離法(Technique for Order Preference by Similarity to an Ideal Solution,TOPSIS)是由C. L.Hwang和K. Yoon于1981年首次提出. TOPSIS是處理真實世界中的多屬性或多標準決策(MADM/MCDM)問題的主要技術之一[11]. 它幫助決策者組織待解決的問題,并對替代品進行分析,比較和排名. 從而進行合理的選擇.

Topsis方法的具體過程如下：

1)對特征矩陣進行規范化處理,得到規格化向量nij,建立關于規格化向量nij的規范化矩陣.

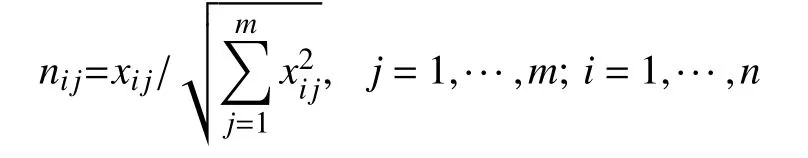
2)通過計算權重規格化值vij建立關于權重規范化值的vij權重規范化矩陣

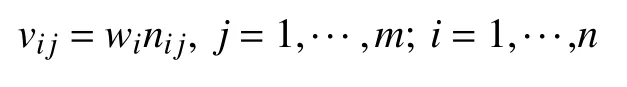
其中,wij是第j個指標的權重.

3)確定正理想解Z+和負理想理Z-

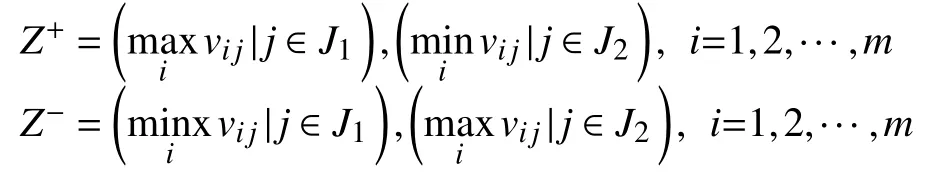
其中,J1為收益性指標集,表示在第i個指標上的最優值.J2是損耗性指標集,表示在第i個指標上的最劣值.收益性指標越大,對評估結果越有利; 損耗性指標越小,對評估結果越有利. 反之,則對評估結果不利.

4)計算距離尺度,即計算每個目標到正理想解和負理想解的距離：

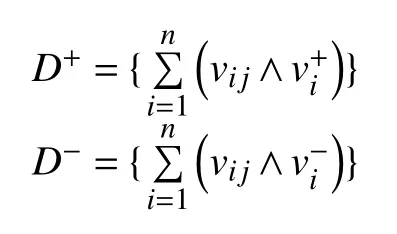
5)計算目標與理想解之間的的相對接近度.

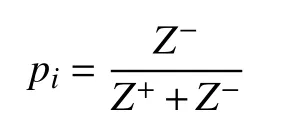
6)排列偏好順序.

2 一種基于相關系數的相似性度量方法在軟件成本評估中的應用

在軟件成本的估算過程中,不同指標之間權重的確定問題尤為重要,大多數相似性度量方法一般根據專家的判斷或者由先驗經驗來確定[12-15],但這種方法主觀性太強,本文采用基于主觀權重和客觀權重的混合權重確定方法,既通過專家判斷,又采用基于信息熵的權重確定方法. 具體方法如下.

假設評估體系中具有n個評價對象,m個評估指標,評價矩陣為：

1) 首先,對評價矩陣A進行標準化處理.

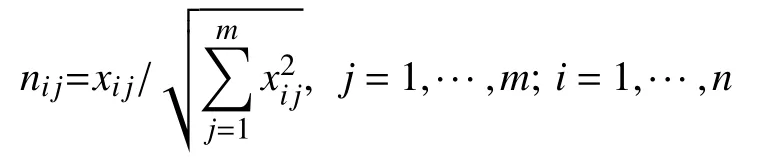
2)確定各個指標之間的權重. 在此我們采用熵權法進行客觀權重的確定,采用熵公式計算每個屬性的平均信息量

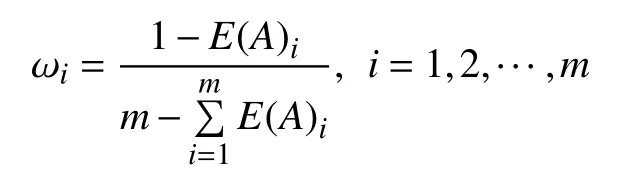
3)設m個評價指標的主觀權重分別為θ1,θ2,···,θj,則第i個指標的真實權重被定義為：

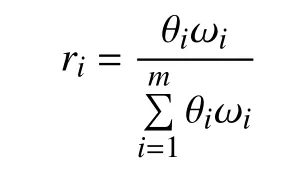
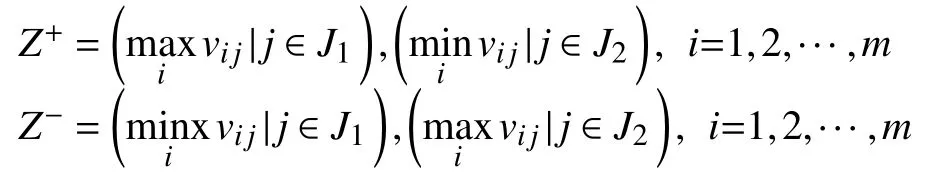
5)計算距離尺度,即采用相關系數計算每個目標A到正理想解和負理想解之間的的距離

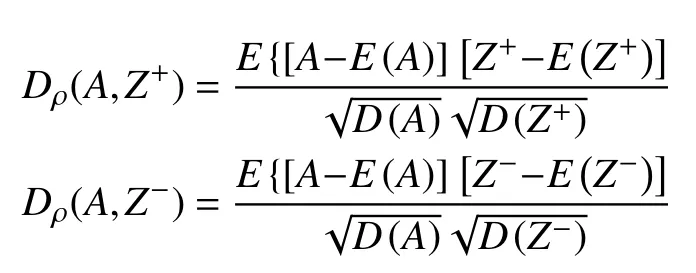
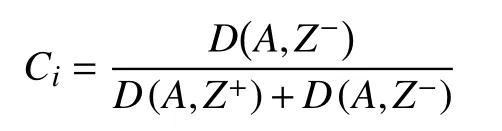
3 實驗驗證

為了檢驗基于本文采用的相關系數度量方法的軟件成本估算方法,設計試驗,并采用公開數據集Desharnais進行本測評實驗,Desharnais數據集是由加拿大軟件行業的統計結果數據,它最早是在1989年由Jean-Marc Desharnais在對項目開發功能點數據的統計分析中應用. 在Desharnais數據集中有12種項目屬性.

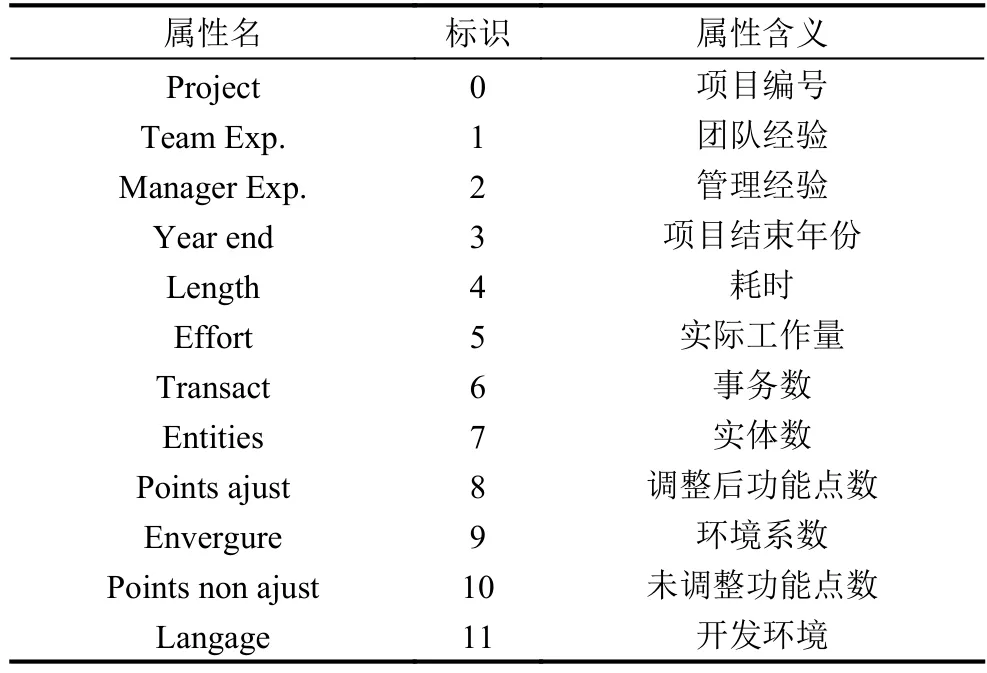
表1 Desharnais數據集的項目屬性

在本實驗中,省略了4個數據不完整的項目,只利用其中77個完整的項目的數據進行試驗.

選取數據集中Team Exp、Manager Exp、Length、Transact、Entities、Points ajust、Envergure、Points non ajust、Langage 9種屬性做為本文軟件成本估算的屬性,Effort屬性作為估算的目標屬性對預測結果的誤差進行計算.

為了驗證成本估算的有效性與準確性,需要引入適當的評價標準. 常用的評價標準有許多,我們采用以下兩種作為標準：

① 平均誤差率(MMRE),用于評估軟件成本估算的平均誤差情況,計算公式如下：

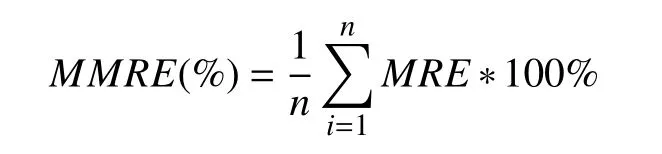
② Pred(x),用于評價成本估算的補充標準,用于計算標準誤差低于x的項目數量在整個數據集中所占的比例.x的值通常設置為25%. 計算公式如下：

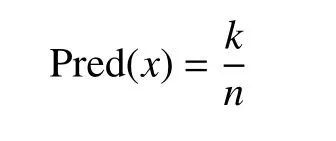
其中,k為標準誤差低于x的項目數量.

為了驗證本文所提方法在軟件方法估算中的準確性,與經典的歐式距離和文獻[16]所提及的相似性度量方法進行比較實驗,比較結果如表2.

表2 實驗結果

從上述實驗結果可以看出,本文提出的基于相關系數度量方法的軟件成本估算方法,在結果上優于經典的歐式距離和文獻[16]提出的相似性度量公式.

4 結論

本文針對軟件工程項目中需求分析階段軟件成本估算問題進行研究,在皮爾遜相關系數的基礎上,綜合考慮了主觀權重和客觀權重,采用TOPSIS方法建立相關模型,提出一種基于相關系數的TOPSIS方法用于軟件成本估算問題研究,并采用公開數據集Desharnais進行試驗驗證. 實驗結果表明,本文所采用基于相關系數的相似性度量方法較以往的方法有更高的準確率.然而,本文所提出的方法和研究工作只是單純聚焦于處理與工作量相關的項目特征而沒有忽略團隊特性、員工發展等主觀因素方面的考慮. 因此,在未來的研究中,會應將包括軟件工程成員的性格、潛力、團隊氛圍等諸多特性充分考慮在內以更加準確地進行軟件成本估算.

1 史濟民,顧春華,鄭紅. 軟件工程：原理、方法與應用. 北京：高等教育出版社,2009.

2 楊芙清. 軟件工程技術發展思索. 軟件學報,2005,16(1)：1-7.

3 The Standish Group. CHAOS report. http：//www.standish group.com. 1995.

4 The Standish Group. 2004 the 3rd quarter research report.http：//www.standishgroup.com,2004.

5 李明樹,何梅,楊達,等. 軟件成本估算方法及應用. 軟件學報,2007,18(4)：775-795.

6 Boehm BW,Valerdi R. Achievements and challenges in software resource estimation[Technical Report]. No.USCCSE-2005-513. http：//sunset.usc.edu/publications/TECHRPT S/2005/usccse2005-513/usccse2005-513.pdf,2005.

7 任雪利. 協同過濾在軟件成本估算中的應用. 計算機系統應用,2014,23(6)：246-249.

8 任雪利,代余彪. 軟件相似度在成本估算中的應用. 計算機應用與軟件,2015,32(6)：34-36,112.

9 曹冬生,王強軍,張元忠,等. 基于類比的軟件成本估算及其一種改進方法. 計算機工程與科學,2009,31(5)：102-106.

10 何慧,張宏莉,張偉哲,等. 一種基于相似度的DDoS攻擊檢測方法. 通信學報,2004,25(7)：176-184.

11 朱永松,國澄明. 基于相關系數的相關跟蹤算法研究. 中國圖 象 圖 形 學 報,2004,9(8)：963-967. [doi：10.11834/jig.200408184]

12 何曉陽,王亞沙. 基于模型的軟件成本估計方法. 計算機研究與發展,2006,43(5)：777-783.

13 Jahanshahloo GR,Lotfi FH,Izadikhah M. An algorithmic method to extend TOPSIS for decision-making problems with interval data. Applied Mathematics and Computation,2006,175(2)：1375-1384. [doi：10.1016/j.amc.2005.08.048]

14 Shih HS,Shyur HJ,Lee ES. An extension of TOPSIS for group decision making. Mathematical and Computer Modelling,2007,45(7-8)：801-813. [doi：10.1016/j.mcm.2006.03.023]

15 周啟超. BP算法改進及在軟件成本估算中的應用. 計算機技術與發展,2016,26(2)：195-198.

16 趙雪芬. 基于未知度的Vague集相似度量方法研究. 計算機工程與應用,2013,49(14)：130-132,216. [doi：10.3778/j.issn.1002-8331.1111-0518]