基于遺傳算法的二維最大類間方差法的優化

， ，

(南京理工大學機械工程學院，江蘇 南京 210094)

0 引言

在計算機視覺理論中，圖像分割、特征提取和目標識別是由低層到高層的3大主要任務，特征提取和目標識別都是以圖像分割為基礎。目前的圖像分割方法主要有基于閾值的分割方法、基于邊緣的分割方法、基于區域的分割方法和基于特定理論的分割方法等。閾值分割法因對圖像的質量要求較低，而且運算過程相對簡單，效果較好，所以在圖像分割中應用最為廣泛。常用的閾值分割法中，最大類間方差法因計算簡單、運算效率高、速度快且得到的閾值較為準確，得到了廣泛應用[1]。

但最大類間差法的缺點也顯而易見，對于目標和背景相差不大的圖像，灰度直方圖呈現雙峰或多峰的情況，使用此方法很容易導致圖像的信息丟失，處理時也只是考慮到了圖像的灰度信息而沒有考慮其空間信息，因此分割后圖像上目標的輪廓在細節上會比較模糊。所以對分割后圖像質量要求較高的情況，一維最大類間方差法顯然是不能滿足要求的[2]。針對一維閾值法的不足，二維最大類間差法引入了鄰域平均灰度信息和像素信息一起構成二維直方圖，通過二維直方圖求解最佳閾值，其準確性和魯棒性得到了很大提升，但與此同時，計算量也成指數形式增長，實時性大打折扣[3]。在此，針對二維最大類間差法存在的問題，將最佳閾值的判別式由二維降到一維，減少計算量，同時通過遺傳算法加快尋優過程，減少了原有窮舉法所帶來的計算量過大的問題。

1 二維最大類間方差法

設大小為M×N的圖像在像素點(x,y)處像素為f(x,y)，灰度級為L，以(x,y)為中心點的k×k(k取奇數)的鄰域的平均灰度值g(x,y)為該點的平均灰度值，其灰度級也為L。f(x,y)和g(x,y)共同組成了一幅圖像的二維直方圖。圖1為一幅測試圖像的二維直方圖(Z軸為像素點個數)。由圖1可以看出，大部分的點灰度值與其鄰域灰度值相差不大，集中在對角線上，遠離對角線的點可能是灰度變化較大的邊界點和噪聲點。圖2為二維直方圖的平面投影圖，假設(s,t)為最佳閾值將投影圖分割成4個部分，其中沿對角線方向上A區域和B區域內元素相近，可分別看作是目標和背景，遠離對角線方向的C區域和D區域可看作是邊界點和噪聲點。

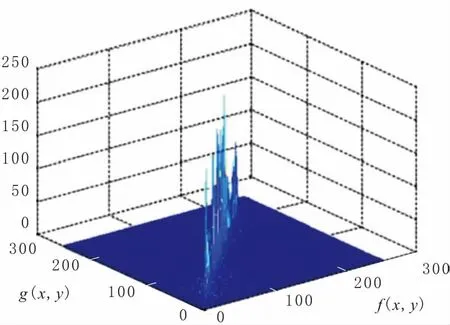
圖1 測試圖像的二維直方圖

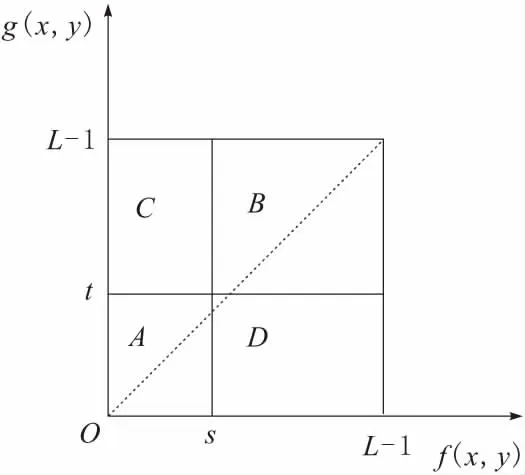
圖2 二維灰度直方圖的投影

記Cij為灰度值為i,鄰域平均灰度值為j的像素點在整幅圖像出現的頻數，其相應的概率密度為Pij，則Pij的計算公式為：

(1)

根據閾值分割的思想，把圖像中的像素點分為目標和背景兩類(對應投影圖中的A區域和B區域)，PA和PB是像素點出現在這兩類區域的概率，則有：

(2)

(3)

A區和B區對應的均值矢量為：

μA=(μAi,μAj)τ=

(4)

μB=(μBi,μBj)τ=

(5)

二維灰度直方圖的總均值矢量為：

μ=(μt,μj)τ=

(6)

實際情況下，邊界點和噪聲點所占的比例很小[3]，大多數情況，目標和背景所占的比例的統計值為0.95～0.98。所以有PA+PB≈1，且有μ≈PAμA+PBμB，在忽略邊界點和噪聲點的情況下等式成立。定義目標類和背景類的離散測度矩陣為σ，有

σ=PA(μA-μ)(μA-μ)τ+

PB(μB-μ)(μB-μ)τ

(7)

計算離散度矩陣的跡作為目標類和背景類的離散度的測度

tr(σ) =[PA(μA-μ)(μA-μ)τ+

PB(μB-μ)(μB-μ)τ]=

PA(s,t)(μAi-μi)2+(μAj-μj)2〗+

PB(s,t)(μBi-μi)2+(μBj-μj)2〗

(8)

使tr(σ)取得最大值時的閾值(s*,t*)即為隨求的最大閾值，即

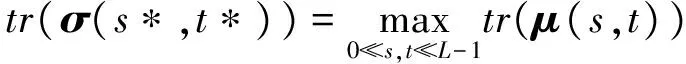
(9)

二維最大類間方差法引入像素的鄰域灰度信息，通過二維直方圖求得最佳閾值，和一維閾值法相比，其抗噪性和準確性顯著提高，與此同時，算法的復雜度也成倍上升。其運算過程需要遍歷整個圖像存在的灰度值，離散度矩陣的計算需要雙重循環，循環體需要在A區和B區做累加運算，次數為s×t+(L-s)×(L-t)，所以其運算復雜度為O(L4)。為了提高效率，可以從兩方面入手：一方面可以簡化其離散度矩陣，減少運算復雜度；另一方面可以加快尋優過程，減少計算量。

2 改進的二維最大類間差法

為了解決算法的計算復雜度問題，本文采用基于二維離散隨機變量的邊緣概率分布的改進算法[4]，對概率密度Pij求其邊緣概率Wi和Wj。

(10)

(11)

Wi為像素灰度值i的一維直方圖分布，Wj為鄰域灰度值j的一維直方圖分布。由一維最大類間方差法的定義可以推導出Wi和Wj的類間方差。

(12)

(13)

因為邊界點和噪聲點所占的比例很小，所以假設C區和D區的概率為零，即有

(14)

將式(14)代入式(2)，可推出

(15)

(16)

所以有:

PA=PAi=PAj

(17)

同理，將式(14)代入式(3)，可得:

PB=PBi=PBj

(18)

將式(17)和式(18)代入式(8)，有

tr(σ)=PA(s,t)(μAi-μi)2+(μAj-μj)2〗+

PB(s,t)(μBi-μi)2+(μBj-μj)2〗=

PAi(μAi-μi)2+PBi(μBi-μi)2+

PAj(μAj-μj)2+PBj(μBj-μj)2=

(19)

由式(19)可知，在忽略邊界點和噪聲點的情況下，二維最大類間方差法求最佳閾值的求解問題可以拆分成求解2個一維閾值之和的形式，復雜度大大降低，增強了時效性。

3 自適應遺傳算法

在遺傳算法中，交叉概率和變異概率的選取是影響遺傳算法收斂速度和尋優結果的重要因素[5]。Srinvivas等提出的自適應遺傳算法中，每一代的交叉和變異概率都會隨著其適應度在每代中的大小而自動調整，使得在保持種群多樣性的同時也保證了遺傳算法的收斂性。自適應遺傳算法的交叉概率Pc和變異概率Pm如下：

(20)

(21)

fmax為每一代種群中的最大適應度值；favg為每一代的平均適應度值；f為變異前的個體適應度值；f′為交叉的2個個體中適應度值較大的個體適應度值；k1,k2,k3,k4為(0,1)之間的調整系數。

從式(20)和式(21)可以看出，當個體適應度值越接近最大適應度值時，交叉和變異的概率越小，當與最大適應度值一致時其交叉和變異的概率為零。這在群體處于后期的時候是可以的，但在進化初期，容易導致適應度高的個體幾乎處于不變的情況，而使得進化過程陷入局部最優解，顯然這是需要避免的[6]。所以在自適應遺傳算法的基礎上，需要對交叉和變異的概率做進一步調整，在保證遺傳多樣性的基礎上，避免進化趨于局部最優解。調整后的交叉概率Pc和變異概率Pm如下：

(22)

(23)

Pc0是最大交叉概率；Pm0是最大變異概率。如式(22)和式(23)所示，一方面交叉和變異概率隨種群的適應度實現自動調整，更好地保留適應度高的個體，另一方面交叉和變異的概率不會為零，避免了陷入局部最優解的問題。

遺傳算法的流程如圖3所示。其主要步驟歸納如下：

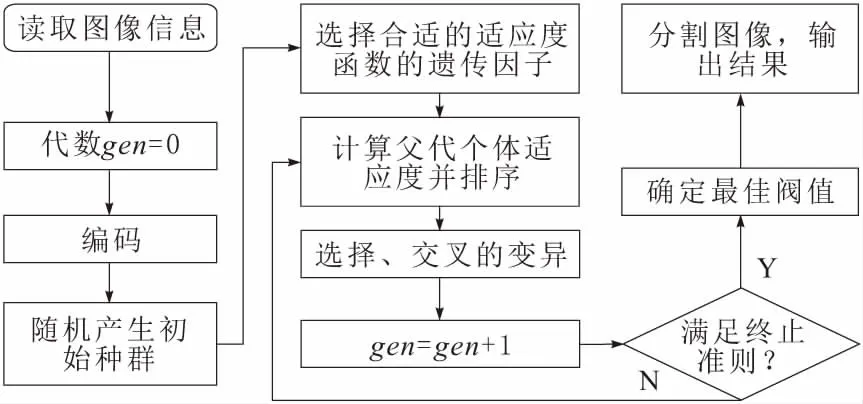
圖3 遺傳算法流程

a.編碼。因為灰度值得范圍是0～255共256(28)個灰度級，通常采用二進制編碼的方式，又有(s,t)2個變量閾值，所以編碼為16位，其中前8位表示像素點的閾值s，后8位表示鄰域閾值t。

b.隨機產生初始種群。初始種群的規模將影響算法的精度和效率。種群規模太小則搜索空間有限，種群規模太大將增加計算時間。本文的種群規模為20。

c.選擇適應度函數。選擇式(19)作為適應度函數計算適應度值。

d.選擇、交叉和變異。采用輪盤賭作為選擇方法。對前8位和后8位采用雙點交叉，交叉和變異的概率如式(22)和式(23)所示，取Pc0=0.9，Pm0=0.1。

e.終止準則。當算法執行到最大代數或經過20代進化后，群體中最高適應度值仍未發生變化，則該個體即為所求閾值編碼。本文實驗確定最大遺傳代數為100代較為合適。

4 實驗驗證

為了驗證算法的正確性，分別采用經典Otsu法、遺傳算法和本文算法對圖片進行分割。實驗的圖片樣本為PCB板，分割結果如圖4所示。

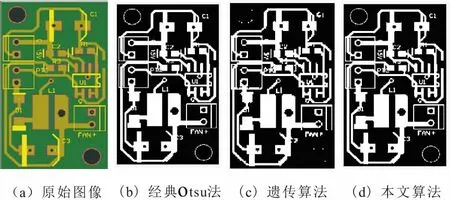
圖4 各類方法圖形處理后的對比

3種算法的閾值以及運行時間結果如表1所示。對分割結果進行分析可以發現經典二維Otsu法和本文算法的分割效果較好，且差距不大，遺傳算法的分割效果相對較差，處理結果可以看出丟失了一些目標信息。由表1可知，和經典二維Otsu算法相比，本文算法在處理速度上大大提高，比經典算法的運算時間節約50%左右，且穩定性相比經典算法也有所提升。遺傳算法的穩定性和經典算法相差不大，但閾值的精確性有所下降，運行速度提升的也很有限。綜上所述，本文算法在運算速度上較之經典算法有很大提高，穩定性也有所提升。

表1 不同方法的圖像閾值及運行時間

5 結束語

針對經典二維最大類間方差法存在的復雜度高，運行時間長的問題，首先通過近似將原有的二階離散度矩陣拆分成2個一階的類間差之和，減少了運算難度，同時引入遺傳算法，將原有的窮舉法搜尋最優解改為由遺傳算法進行尋優，加快尋優過程，進一步提高運算效率。實驗證明，本文算法較之經典算法，效率上有較大提升，運算時間減少約50%，同時，在保證精確度的同時，穩定性也有所提升，使最終結果穩定在2個像素，大大改善了經典算法的實時性，提升了穩定性，具有推廣價值。

參考文獻：

[1] 胡藝,楊帆,潘國峰. 一種改進的印刷電路板缺陷檢測分割算法[J]. 科學技術與工程,2017,17(9):221-228.

[2] 王福斌,李迎燕,劉杰,等. 基于OpenCV的機器視覺圖像處理技術實現[J]. 機械與電子,2010,28(6):54-57.

[3] 吳一全,樊軍,吳詩婳. 改進的二維Otsu法閾值分割快速迭代算法[J]. 電子測量與儀器學報,2011,25(3):218-225.

[4] 劉金,金煒東.噪聲圖像的快速二維Otsu閾值分割[J].計算機應用研究,2013,30(10):3169-3171,3200.

[5] 李賢陽,黃嬋. 一種結合改進Otsu法和改進遺傳算法的圖像分割方法[J]. 實驗室研究與探索,2012,31(12):57-61,112.

[6] 吳昊,汪榮貴,方帥,等. 基于最小類內差和最大類間差的圖像分割算法研究[J]. 工程圖學學報,2011,32(1):67-75.