修正Durrmeyer型Bernstein-Stancu算子的逼近

徐華，錢程

(1. 杭州師范大學錢江學院， 浙江 杭州 310036； 2. 杭州師范大學 理學院， 浙江 杭州 311121)

0 引 言

以C[0,1]表示定義在閉區(qū)間[0,1]上連續(xù)函數(shù)的全體，對于任意f∈C[0,1]的函數(shù)，其對應的Bernstein算子和Bernstein-Durrmeyer算子分別定義如下：

其中，

這2類算子在逼近論和計算數(shù)學等領域有許多重要的應用，對其逼近性質(zhì)的研究也已經(jīng)相當廣泛. 2010年，GADJIEV等[1]定義了以下推廣形式的Bernstein-Durrmeyer型算子：

其中，αk,βk,k=1,2為滿足以下條件的正常數(shù)： 0≤α1≤β1,0≤α2≤β2,而

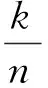
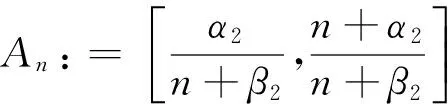
最近，DONG等[4]引入了下列基于Sn,α,β(f,x)的Durrmeyer型算子：

其中，

由于(lemma 1[3])

(1)

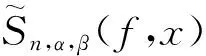
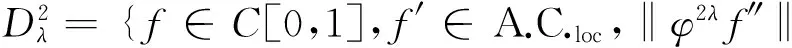
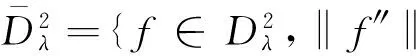
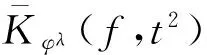
t4/(2-λ)‖g″‖},

(2)

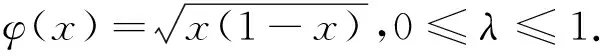
(3)

其中x～y意為存在正常數(shù)c使得c-1y≤x≤cy.

本文的主要結(jié)論為：

定理1設f為[0,1]區(qū)間上的連續(xù)函數(shù)，0≤λ≤1. 則存在一個僅依賴于λ,α1,α2,β1,β2的正常數(shù)C，使得

其中，

而ω(f,t)為f在[0,1]上的通常連續(xù)模.

文中，C總表示一個絕對正常數(shù)或僅依賴于某些參數(shù)(除f,n和x以外)的正常數(shù)，其值在不同地方可以不同.

定理2設f為[0,1]區(qū)間上的連續(xù)函數(shù)，0<α<2/(2-λ),0≤λ≤1,則

意味著

(ii)ω(f,t)=O(tα(1-λ/2)).

1 引理及證明

引理1對于任意γ≥0，有

x∈[0,1].

證明利用文獻[3]中的引理1，對任意γ≥0，有

因此，

由此，引理1得證.

引理2對任意x∈[0,1]，有

證明記

由文獻[6]有

且有

(5)

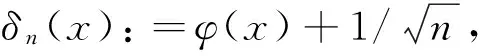
注意到(見文獻[4])：

Δn(x)～δn(x),x∈[0,1].

(6)

由式(5)即得

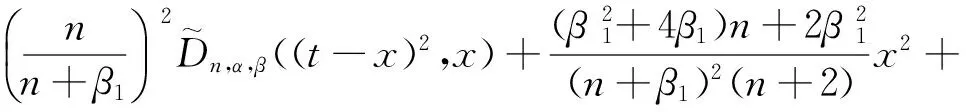
引理2得證.

引理3對任意x∈[0,1]，有

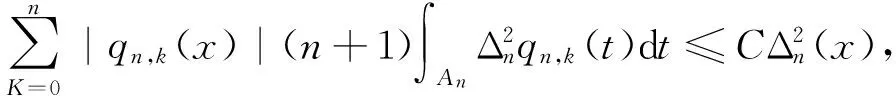
(7)

(8)

證明直接計算，得

又因為

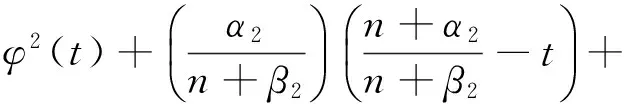
第2階段，繼續(xù)推進“四同步”工作機制，以副中心道路新建、改建和擴建為契機，全面推進城市副中心新城155 km2智慧交通管理科技系統(tǒng)建設.

所以

由此，

(9)

若x∈[0,1]An，不妨設

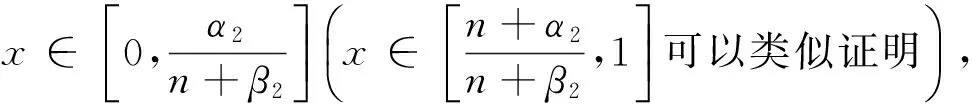
(10)

若x∈An，則有

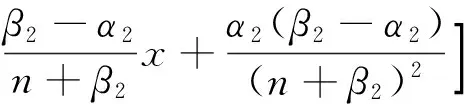
(11)

綜合式(9)～(11)，即得式(9).

下證式(8).由式(6)知：

因此，

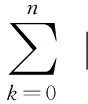
置

Cα,λ={f∈C([0,1]),‖f‖0<+};

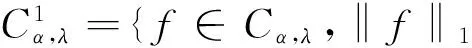
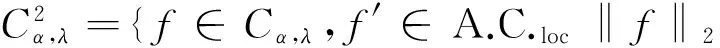
引理4如果0≤λ≤1,0<α<2,則

(12)

(13)

證明分2種情形證明式(12).

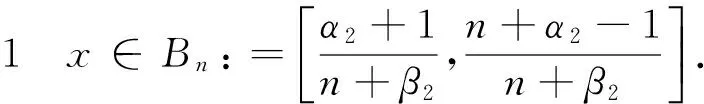
Δn(x)～φ(x),x∈Bn.

(14)

通過簡單計算可得

(15)

其中，

(16)

由式(13)～(16)得

由引理1和引理3，得

情形2

此時，顯然有

注意到

其中,qn-1,-1(x)=qn-1,n(x)=0,故有

利用式(16)并使用H?lder不等式2次，得到

上式第4個不等式利用……