淺談初中數學幾何問題解題方法
孫大平
(安徽省臨泉縣高塘鎮高塘中心校 236400)
一、打好初中幾何學習的理論基礎
初中幾何學習,由于是一門相對比較連貫的基礎性學科,在學習的過程中要理清整個幾何學習的理論基礎.由于幾何學習的原理和定理比較多,因此,在整個初中幾何學習的過程中做好學習的理論準備,夯實全過程的幾何學習基礎.就比如說,在幾何學習的過程中,如果想讓學生理解射線這一抽象的幾何概念,在黑板上畫出等額的射線,然后圍繞射線講解有關于幾何線段、射線以及由線條所組成的各個圖形之間的關系,從而將理論知識點趣味性的引出,加深初中生學習幾何知識的印象.
二、樹立初中幾何學習的自信心
萬事開頭難,初中數學幾何教學也是一樣,樹立初中幾何學習的自信心必須結合之前就應該做好相關的工作,磨刀不誤砍柴工,教師應該讓學生意識到初中幾何知識的重要性,了解幾何學習的變遷和發展,通過多媒體課件模擬的方式,讓學生明白幾何知識在國家各項事業發展方面所作出的積極貢獻.利用有趣的道具來教導學生進行趣味幾何認知和學習,培養學生勤動手、勤動腦、勤拆分的實踐和動手能力.通過將幾何知識和理論與生活實踐對比學習,學生在學習過程中動手和動腦的培養,就可以讓學生更好地加強學習的自信心,有利于擴大學生的知識面,有利于學生整體素質的提升,成為初中幾何學習過程中的小主人.
三、分清在教學過程中容易混淆的幾何概念
在學習幾何的過程中,老師可以幫助學生,按照一定的方法和線索來整理錯題本,尤其是對于幾何學習過程中的一系列難題,鼓勵學生將正確的方法畫出來,記錄錯題的原因和解題的要點.通過反復記憶和培訓來打破傳統認知中錯誤的觀念.因此在教學的過程中應該鼓勵學生積極動手,養成自己主動記錄錯誤,分清混淆基礎概念的良好習慣,從而可以在課堂之后、在老師不在場的情況下也能夠通過教材和錯題本的輔助,做好整體知識結構和知識要點的掌握工作,并及時總結發現自身學習過程中的薄弱環節.
四、關注思想方法,由難化易,優化幾何問題解析
幾何圖形語言是教學過程及應用實踐的重要因素,運用圖形語言表達,對數學思維及交流規范和描述活動,是用于規范和描述的問題關鍵性環節,用數學的幾何語言來充實課堂,提高學生思維能力.幾何圖形由于經常變化多端,因此其方法也是變化莫測,即所謂的數學變形金剛.雖然題目變化莫測,但是解法卻是萬變不離其宗的,每道題目都有一定的法規和規律,都有其相應的解法,因此建立幾何模型是非常有效的,能夠促進學生對幾何模型的理解和認識.由淺及深,層層遞進.則淺的即為基本的圖形形狀,看到相似的形狀或是相似的題目,就能聯想到一定解題思路,這就是簡單的模型思想.深的即為看到一些相似題目或是關鍵點就能推理和演繹出正確的解法.初中數學幾何知識幾乎貫穿整個初中,是初中數學的重要精神支柱,因此提高初中生的邏輯思維能力和想象力是極其重要的.能有效地提高學生對幾何的思想看法.幾何教學是初中教學的重要組成部分,是學生首次接觸和了解邏輯思維體系的一條重要紐帶,也是促進初中數學教學目標的一個重要橋梁.平時要培養學生多積累,勤思考,遇到難題時才能有備無患,胸有成竹.因此老師要培養學生不僅僅只是認識圖形,還要學會腦補圖形,甚至還可以通過補全圖形來完成解題.
五、數形結合、解決解析幾何問題
在中學數學的研究中,數和形之間存在著密不可分的聯系聯系,需要探求其中的規律,結合圖形來進行數據的賦值給予.解決解析幾何問題:幾何基本問題和基本方式,也可以通過數形結合的方法來解決數據結構,此方法最大的優點就在于靈活性的思想對應,將點線面曲線的性質和相互特性可以對應分析.
在三角形中解決幾何問題時,要考慮中位線.如果已知一邊中點,第一步要考慮找到另一條邊的中點,將兩點連線,這條線便是該三角形的中位線.中位線的特點是,平行并等于第三條邊的一半.
比如下面這道例題:
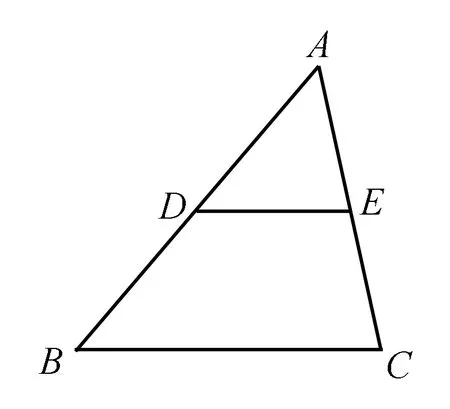
例已知三角形ABC中,點D是線段AB的中點,點E是線段AC的中點,證明DE=BC
分析有題可知點D和點E分別是線段AB和線段AC的中點,所以線段DE是三角形ABC的中位線,所以線段BC的長度等于兩倍線段DE的長度)
解∵D和E分別是AB和AC的中點,
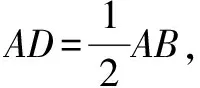
且∠DAE=∠BAC,
∴△ABC∽△ADE,
此題利用數形結合的思想解決問題,使運算過程變得簡單,從圖形上可直觀地看出所求結果.數形結合思想還可以應用在其它曲線的解題思路.
六、結束語
初中數學幾何教學學習的過程中,教師應該加強對于學生勤勉學習能力、積極進取思維的培養.對于學生的理解能力和概念內涵的準確把握,能夠培養初中生對于幾何試題產生類似條件反射的學習能力,從而對于積極學好初中數學幾何學科起到很好的作用.
參考文獻:
[1]易建祥.初中生求解動態幾何問題的典型錯誤及對策研究[D].重慶:重慶師范大學,2016.
[2]陳小春.初中數學數形結合題型的解題技巧[J].數理化解題研究(初中版),2014(11):17.

