猶豫模糊信息下的協(xié)相關度與聚類分析*

汪 峰，毛軍軍，祖 璇，鄒 斌

1.安徽大學 數(shù)學科學學院，合肥 230601

2.安徽大學 計算智能與信號處理教育部重點實驗室，合肥 230039

3.安徽師范大學 皖江學院 經(jīng)濟系，安徽 蕪湖 241008

4.安徽廣播電視大學 教育科學學院，合肥 230022

1 引言

由于客觀世界的復雜性和個人認知水平的差異性，針對同一問題往往有不同的看法，有時很難達成一致。例如在經(jīng)濟管理與決策問題中，討論備選方案滿足某一準則時，有些專家給出的隸屬度值是0.6，有些專家認為是0.7，還有些專家堅持0.8比較合理。他們觀點不一，又難以說服對方。又如決策者在做決策時常常表現(xiàn)出猶豫不決和優(yōu)柔寡斷的狀態(tài)，這時用來描述決策信息的模糊集的隸屬度用一個確定的值來刻畫很難反映決策者的真實情況。為此，Torra和Narukawa[1-2]提出了另一種廣義模糊集——猶豫模糊集。猶豫模糊集的隸屬度是由一些可能的數(shù)值組成的集合，這樣可以兼顧決策者的不同偏好，得到更合理全面的決策結果。更為重要的是，它避免了使用各種算子來合成各專家提供的數(shù)據(jù)，能直觀描述不同決策成員給出的意見，因而可以直接反映和處理它們，從而減少了數(shù)據(jù)的流失。Torra等人在文獻[1-2]討論了猶豫模糊集與直覺模糊集[3]、二型模糊集[4]和模糊多集[5]之間的區(qū)別與聯(lián)系，指出猶豫模糊集包含直覺模糊集，它是二型模糊集的特例，與模糊多集形式上相同，但運算法則不同。猶豫模糊集自誕生以來，發(fā)展速度很快，其中徐澤水和夏梅梅及其團隊[6-10]為猶豫模糊集的進一步研究做出了重要貢獻。

熵和相關性測度是模糊集理論中兩個重要的研究課題，其理論早被應用到諸如數(shù)據(jù)分析、模式識別、聚類分析、決策以及圖像處理等許多領域。從原先熱學上的熵到信息論中的信息熵、相對熵，再到模糊集上的模糊熵、直覺模糊熵、猶豫模糊熵，最終形成了一套公理化體系。其中交叉熵測度主要度量兩個集合的區(qū)別信息，吸引了眾多學者對其進行研究。文獻[11]提出了一些直覺模糊環(huán)境下的交叉熵和直覺模糊熵的公式，并把它們運用到群決策當中。文獻[12-15]給出了熵、交叉熵、距離測度和相似性側度之間的聯(lián)系以及公理化定義，并把它們應用到區(qū)間值模糊集上。文獻[16]將模糊集的熵、交叉熵推廣到猶豫模糊環(huán)境下，給出猶豫模糊集的熵測度、交叉熵測度及其公理化形式，并討論了猶豫模糊集的熵、相似度以及交叉熵之間的關系，最終將它們應用到多屬性決策中。Gerstenkorn和Manko[17]把統(tǒng)計學中相關系數(shù)的概念推廣到直覺模糊集上，Hong和Hwang[18]又把它們定義到概率空間上。文獻[19]通過重心法來計算直覺模糊集的相關系數(shù)，此后又有學者將相關系數(shù)推廣到區(qū)間型直覺模糊集上[20-21]。文獻[22]仔細分析了猶豫模糊信息下距離與相關度的關系，提出了基于距離的相關度公式，該公式構造合理，易被人們接受，但其結構不精，適用面不寬，很多情形下與事實不符。文獻[23]提出了基于距離的猶豫模糊相似度公式，但公式的分辨率不夠高，度量結果有時與實際情況相差很大。文獻[24]把信息論中的相對熵遷移到猶豫模糊集上，并把猶豫模糊相對熵對稱化，提出對稱交互熵，針對基于距離的相似度公式的缺陷，利用對稱交互熵定義一種新的相似度公式。文獻[25]將直覺模糊集的相關性測度延伸至猶豫模糊環(huán)境下，定義并證明了猶豫模糊集的兩種相關系數(shù)，但這種相關系數(shù)實際上是基于向量的觀點，會出現(xiàn)即使兩個樣本不同，其相關系數(shù)也可能為1的情況。

聚類是把一系列的對象、方案或事件等分成若干個類的過程，每個類中對象的特征比其他類有更高的相似性。聚類分析是利用數(shù)學的方法按照確定的標準對客觀事物進行分類，將樣本的相似程度作為劃分原則，這樣選擇合適的相似度就成為聚類的關鍵。隨著信息時代的到來，特別是在大數(shù)據(jù)趨勢下，聚類分析作為信息處理的重要一步，越來越受到人們的重視。因為現(xiàn)實的分類往往伴隨著模糊性，所以用模糊理論來進行聚類分析會顯得更自然，更符合客觀實際，因此便產(chǎn)生了模糊聚類分析。面對不同的模糊環(huán)境，人們提出了各種聚類算法來處理不同類型的模糊數(shù)據(jù)，如直覺模糊聚類算法[26-28]、二型模糊聚類算法[29-30]等。在猶豫模糊情形下，文獻[24]是通過編網(wǎng)的聚類方法，在利用相似度公式計算得到的關聯(lián)矩陣上直接進行表上作業(yè)，此方法快速有效，操作簡單，直觀性很強，但它所有的聚類邊界或者是水平的，或者是豎直的，沒有對角的邊界，結構單一，過程粗糙，且當樣本容量較大時，容易產(chǎn)生混亂甚至無法進行操作，同時它很難利用計算機進行程序設計，這種直觀分類在一定程度上降低了聚類的質量和準確性；文獻[25]利用導出的相關系數(shù)公式構造相似矩陣，通過平方法獲得等價矩陣，進而對樣本數(shù)據(jù)進行聚類分析，采用經(jīng)典方法聚類，但聚類結果不夠精細，與事實不是特別吻合。

針對以上問題，本文首先從文獻[16]關于猶豫模糊元的公理化定義出發(fā)，構造任意兩個猶豫模糊元新的交叉熵公式，把它作為一種距離，并與文獻[23]中的各種距離公式進行比較，突出其優(yōu)勢所在。然后基于此交叉熵距離，在屬性權重完全未知的情況下，根據(jù)離差最大化[31]原則建立非線性規(guī)劃模型得到屬性權重公式。接著由概率統(tǒng)計[32]中相關系數(shù)的定義結構，得出猶豫模糊集的協(xié)相關度公式，并證明了它與一般相關系數(shù)類似的性質。考慮到論域里不同元素對結果的影響不同，故將協(xié)相關度加權（權重通過得出的屬性權重公式獲得），最后利用加權的協(xié)相關度公式構造協(xié)相關矩陣，再把協(xié)相關矩陣轉化為等價矩陣，進而做聚類分析。

2 概念準備

定義1[1-2]設X是一個給定的集合，稱為論域，則二元組A={x,hA(x)|x∈X}稱為定義在X上的一個猶豫模糊集。其中hA(x)是區(qū)間[0,1]上若干個不同的數(shù)組成的集合，表示元素x屬于集合A若干個可能的隸屬度。為表述方便，把有限論域X上的全體猶豫模糊集記為HFS(X)，稱hA(x)為A的猶豫模糊元，簡寫為hA。

特別地，當猶豫模糊集的每一個猶豫模糊元都只有一個元素時，則猶豫模糊集就退化為普通模糊集。可見猶豫模糊集是普通模糊集的推廣，這里主要是隸屬度的推廣，由一值變?yōu)槎嘀怠?/p>

值得注意的是，不同的猶豫模糊元中元素的個數(shù)可能不同且這些元素的排列順序通常是紊亂的，為便于不同猶豫模糊元的比較與運算，這里做出規(guī)定：

（1）所有元素統(tǒng)一按升序排列。令σ:(1,2,…,n)→(1,2,…,n)為一個排序，使得hσ(j)(xi)＜hσ(j+1)(xi)，即 ?xi∈分別表示hA(xi)和hB(xi)中第j小的元素，當且僅當時，有hA(xi)=hB(xi)。

（2）用l(hA(xi))、l(hB(xi))分別表示hA(xi)和hB(xi)中元素的個數(shù)，令li=max{l(hA(xi)),l(hB(xi))}，若l(hA(xi))≠l(hB(xi))，則在元素少的集合里重復添加元素，使得該集合的元素個數(shù)達到li。添加的原則依據(jù)決策者的風險偏好：喜好風險的決策者會對預期結果有比較樂觀的估計，通常添加該集合中最大的元素；而厭惡風險的決策者對預期結果的估計一般比較悲觀，則是添加該集合中最小的元素。為方便起見，本文不妨統(tǒng)一采用樂觀準則添加元素。例如兩個猶豫模糊元：hA(x1)={0.2,0.4},hB(x1)={0.3,0.5,0.6}，很明顯l(hA(xi))＜l(hB(xi))，為保證運算能夠進行，將hA(x1)擴充為hA(x1)={0.2,0.4,0.4}。

為了度量不同猶豫模糊集的區(qū)別信息，這里引入交叉熵的概念。文獻[16]給出了兩個猶豫模糊元的交叉熵的公理化定義。

定義2[16]設α、β是任意兩個猶豫模糊元，則它們的交叉熵C(α,β)應滿足下面兩個公理化條件：

（1）C(α,β)≥ 0

（2）C(α,β)=0?ασ(i)=βσ(i),?i=1,2,…,l

按照以上定義方式，構造任意兩個猶豫模糊元的交叉熵公式。

定義3設hA(xi)、hB(xi)分別為猶豫模糊集A和B的猶豫模糊元，?xi∈X，X={x1,x2,…,xn}，則稱：

為猶豫模糊元hA(xi)和hB(xi)的交叉熵，簡記為C(hA,hB)。

由定義3交叉熵的結構，不難得到下面的定理。

定理1設 ?A,B∈HFS(X)，hA、hB分別是A和B的猶豫模糊元，則C(hA,hB)滿足：

（1）C(hA,hB)≥ 0

（2）C(hA,hB)=0 ?hA=hB，即X,j=1,2,…,li

（3）C(hA,hB)=C(hB,hA)

證明令：

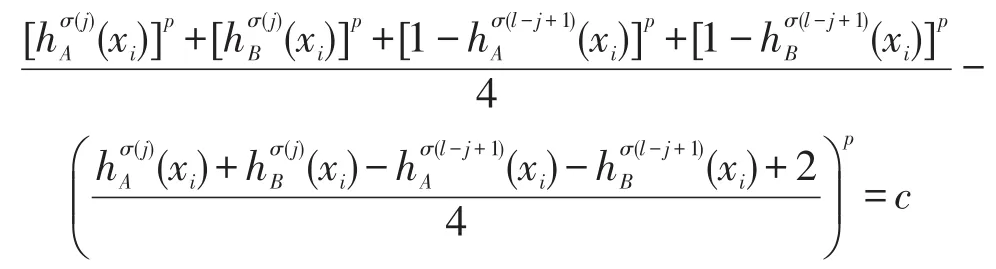
（1）要證C(hA,hB)≥0，只需證c≥0。設f(x)=xp,0≤x≤ 1且p＞1，則f″(x)=p(p-1)xp-2≥ 0，即f(x)是下凸函數(shù)，因此有Jensen不等式成立：

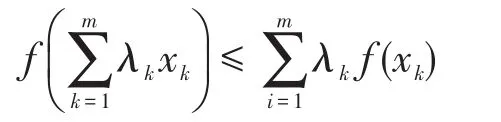
因此有c≥0，又，故C(hA,hB)≥ 0。

（2）若兩個猶豫模糊元hA=hB，即=,j=1,2,…,li,顯然有C(hA,hB)=0；若C(hA,hB)=0，則必有c=0。由Jensen不等式等號成立的條件，當且僅當x1=x2=x3=x4時，等式成立，即當?xi∈X,j=1,2,…,li，時，等號成立，這時有hA=hB。

（3）結論顯然。

由定理1可知，定義3中的交叉熵實際上是一種距離測度，因此可以把C(hA,hB)看作兩個猶豫模糊元hA和hB的距離。C(hA,hB)越大，表示hA與hB的差別越大，反之說明hA與hB越接近。在猶豫模糊信息下，關于距離的定義很多。文獻[23]給出了很多猶豫模糊元距離的公式，但本文提出的交叉熵距離在許多情形下特別是當兩個猶豫模糊元比較接近的時候，具有更高的分辨效果。

例設X={x1,x2}，定義在X上的3個猶豫模糊集A、B、C分別為：

比較這3個猶豫模糊集不難發(fā)現(xiàn)，猶豫模糊元hA(x1)與hB(x1)，hA(x2)與hB(x2),hB(x2)與hC(x2)它們相互間的隸屬度很接近，因此在直觀上A與B的差別程度就比B與C小，B與C的差別程度比A與C小。

利用文獻[23]中的廣義加權平均猶豫模糊距離公式：

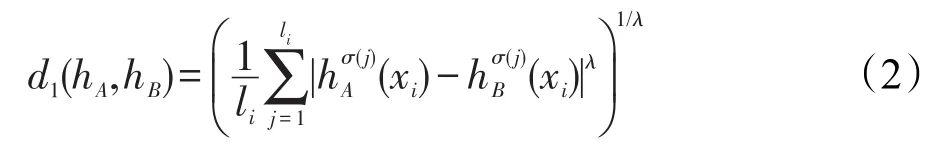
λ=1，式（2）是歸一化Hamming距離；λ=2，式（2）變成歸一化Euclidean距離。

廣義Hausdorff猶豫模糊距離：

λ=1，式（3）是Hamming-Hausdorff距離；λ=2,式（3）變?yōu)镋uclidean-Hausdorff距離。

在實際應用中，有時還要度量猶豫模糊集之間的差別信息，為此定義：

d(A,C)、d(B,C)、di(A,C)、di(B,C)可類似定義。分別利用式（1）、（2）、（3）計算hA與hB,hB與hC,hA與hC的距離，最終各猶豫模糊集間的距離如表1和表2所示。

Table 1 Generalized hesitant fuzzy distance under different parameters表1 不同參數(shù)下的廣義猶豫模糊距離

Table 2 Cross-entropy distance under different parameters表2 不同參數(shù)下的交叉熵距離

從表1、表2可以看出，若用式（3）計算它們的距離，無論λ取1還是2，其結果都是0.1，與直觀認識不符；用式（2）計算A與C的距離，λ取1和2，其值也都是0.1，由于這是一個靜態(tài)的值，這就意味著無論猶豫模糊集B是怎樣的，在比較A與B，B與C的相似程度時，式（2）失去了意義。最后看本文提出的式（1），觀察各個值可以看到，用式（1）算出的結果沒有出現(xiàn)上述對象間差別程度相同的情況。可以大致看出A、B、C兩兩之間的距離（比如在比較A與B，B與C之間的距離時），總體來看式（1）得出的結果表示的相互差異性最大（盡管A、B、C比較接近），這意味著相比于傳統(tǒng)意義上的距離，新型的交叉熵距離的靈敏度更高，其表征的差異度明顯。因此，用式（1）作為猶豫模糊元的距離是很合理的。

3 基于交叉熵的屬性權重確定方法

在多屬性決策中，不同的屬性對最終的決策起著不同的作用，應當賦予不同的權重。對于屬性信息完全未知的多屬性決策問題，需要從決策矩陣中挖掘出屬性權重信息。本文提出的交叉熵既然可視作一種距離，那么就用這種距離來反映對象間的離差（上文已說明這種離差差別反映明顯，因此用在此方法上很合理），由離差最大化方法獲取屬性權重。若所有對象在某屬性下的屬性值差異越小，說明該屬性對決策結果所起的作用越小；反之，如果某屬性能使所有對象的屬性值有較大差異，則說明其對決策起重要作用。因此，從決策的角度考慮，對象屬性值偏差越大的屬性應該賦予越大的權重。

設對象集A={A1,A2,…,Am},屬性集X={x1,x2,…,xn}，權重向量w=(w1,w2,…,wn)T。用dijk表示在屬性xk下，對象Ai與Aj在相應猶豫模糊元間的交叉熵距離，即dijk=C(hAi(xk),hBj(xk))。令Dk(w)=(k=1,2,…,n)，表示對屬性xk而言，所有對象與其他對象的總離差。

根據(jù)上述分析，加權向量w的選擇應使所有屬性對所有對象的總離差最大。為此，可建立如下的優(yōu)化模型：

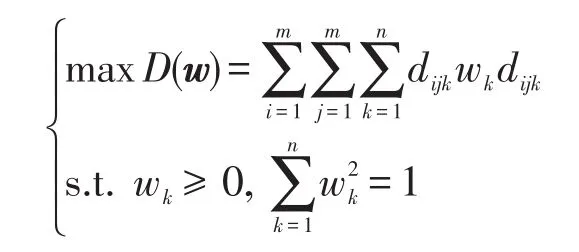
解此模型，作Lagrange函數(shù)：

然后將函數(shù)L分別對wk和ξ求偏導，并令之為0，得：

由此得到：

再將權重歸一化，得：

從式（4）可以看出，在屬性xk下，各對象間的總離差越大，該屬性的權重就越大，反之相應的權重越小。因此，式（4）的結果符合上述權重分配的要求。

4 猶豫模糊集的協(xié)相關度

在統(tǒng)計學中，兩組數(shù)據(jù)X和Y的相關系數(shù)定義為：

其中cov(X,Y)=E{[X-E(X)][Y-E(Y)]}表示隨機變量X和Y的協(xié)方差；D(X)=E[X-E(X)]2,D(Y)=E[Y-E(Y)]2分別表示X和Y的方差。

鑒于這種構造思想，可以類比得出兩個猶豫模糊集的協(xié)相關度。

定義4設A={xi,hA(xi)|xi∈X},B={xi,hB(xi)|xi∈…,li},hB(xi)={hσ(j)B(xi)|j=1,2,…,li},X={x1,x2,…,xn}，則A與B的協(xié)相關度：

其中：

定理2?A,B∈HFS(X),R(A,B)都滿足：

（1）R(A,B)=R(B,A)

（2）-1≤R(A,B)≤ 1

（3）A=B?R(A,B)=1

證明（1）由R(A,B)公式定義的結構，結論顯然成立。

（2）由Cauchy-Schwarz不等式：

（3）顯然成立。

由定理2知，R(A,B)∈[-1,1]。當R(A,B)＞0 時，表示猶豫模糊集A與B正相關，其值越大表明它們的相關性就越大；當R(A,B)＜0時，說明A與B負相關，其值越小表示它們的這種負相關性越強。簡而言之，當|R(A,B)|越靠近1時，認為A與B的相關性越強。

在實際應用中，論域里不同的元素占有不同的地位，應賦予不同的權重。設元素xi(i=1,2,…,n)的權重為wi，滿足且wi∈[0,1]，故在式（5）的基礎上，將協(xié)相關度公式加權：

同樣地，Rw(A,B)也滿足下面的性質：

（1）Rw(A,B)=Rw(B,A)

（2）-1≤Rw(A,B)≤ 1

（3）A=B?Rw(A,B)=1

證明過程與定理2類似，這里不再贅述。

5 基于猶豫模糊協(xié)相關度的聚類分析

5.1 知識準備

定義5設A1,A2,…,Am是m個猶豫模糊集，稱R=(ρij)m×n為協(xié)相關矩陣，其中ρij=Rw(Ai,Aj),i=1,2,…,m,表示兩個猶豫模糊集Ai與Aj的協(xié)相關度，滿足：

（1）0≤ρij≤ 1

（2）ρii=1

（3）ρij=ρji

從定義5可以看出，協(xié)相關矩陣是主對角元全為1的對稱矩陣，且所有元素均在0到1之間，因此協(xié)相關實際上是一種相似關系。

定義6設R=(ρij)m×n是一個協(xié)相關矩陣，稱Rα=(ρij(α))m×n為α-截矩陣，其中：

顯然協(xié)相關矩陣的α-截矩陣是一個布爾矩陣。

定義 7[28]設R=(ρ)是一個協(xié)相關矩陣，稱ijm×mR2=R°R=(ij)m×m為協(xié)相關矩陣的復合（乘積），其中

聚類分析的基本思想是用相似性尺度來衡量事物之間的親疏程度，并以此來實現(xiàn)分類。由普通聚類可知，同類元素具有等價關系，因此在進行模糊聚類分析前必須建立模糊等價關系，其實質是根據(jù)研究對象本身的屬性來構造模糊矩陣。基于相似關系下的模糊矩陣當然是相似矩陣，而本文主要應用模糊等價關系將對象聚類，因此必須把協(xié)相關關系下的相似矩陣改造成模糊等價矩陣。改造方法很多，本文采用平方法：R→R2→(R2)2→…→R2k→…，直到。這時，模糊等價矩陣（R的傳遞閉包）

5.2 猶豫模糊聚類途徑方法

設A={A1,A2,…,Am},X={x1,x2,…,xn},w=(w1,w2,…,wn)T依次為對象集、屬性集和權重向量。決策專家組對所有對象按各屬性進行測度，得到猶豫模糊決策矩陣D=(hij)m×n,hij=hAi(xj)。在進行對象聚類分析前，需要對猶豫模糊決策矩陣D=(hij)m×n進行規(guī)范化處理，以消除各屬性指標的量綱差別和數(shù)量級差別帶來的影響。本文假設決策矩陣D已經(jīng)過標準化處理。

有了以上各節(jié)的討論，便可以給出猶豫模糊環(huán)境下基于等價關系的聚類途徑，具體步驟如下：

（1）利用式（1）計算任意兩個猶豫模糊集Ai與Aj在屬性xk下的交叉熵dijk，利用式（4）計算屬性xk的權重wk(k=1,2,…,n)。

（2）利用式（7）計算Ai與Aj加權的協(xié)相關度Rw(Ai,Aj)，構造協(xié)相關矩陣R。

（3）利用平方法將協(xié)相關矩陣R改造成等價關系矩陣t(R)。

（4）利用t(R)對所有對象進行聚類處理，給定不同置信水平α，求α-截矩陣t(R)α。一個α水平截矩陣就代表一種聚類，其方法是：布爾矩陣t(R)α的第i行（列）的所有元素與第j行（列）的相應元素都相等，那么Ai與Aj就歸為一類。很明顯，當α=1時，所有對象自成一類，隨著α值的降低，對象由細到粗逐漸被歸并，當α從1變化到0時，其分類數(shù)從m類變化到1類，最后形成動態(tài)聚類譜系圖。

5.3 算例分析

某電腦大賣場欲對7種不同的電腦Ai(i=1,2,…,7)進行分類，需要考慮4個因素：價格x1，功能x2，服務x3，質量x4。決策組分別從這4個因素對這7種電腦進行評價，其決策信息以猶豫模糊集的形式給出，組成決策矩陣D=(hij)7×4，hij表示對象Ai滿足屬性xj的被評估值，如表3所示。

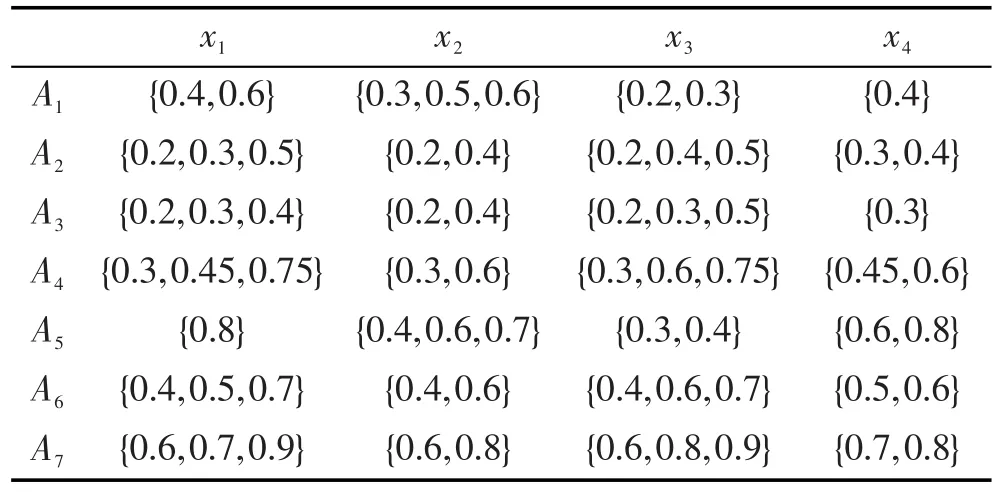
Table 3 Hesitant fuzzy decision matrix表3 猶豫模糊決策矩陣

（1）計算同一個屬性下任意兩個猶豫模糊元的交叉熵（由于決策矩陣牽涉到7個對象在4個屬性下的交叉熵距離，數(shù)量龐大，故這些數(shù)據(jù)不再列出）。然后由式（4）得到屬性權重w=(0.312 0,0.163 7,0.273 3,0.250 9)T。

（2）根據(jù)式(7)得到任兩種電腦Ai與Aj(i,j=1,2,…,7)加權的協(xié)相關度Rw(Ai,Aj)，其協(xié)相關矩陣為：

（3）利用Matlab軟件計算得到矩陣：

因此模糊等價矩陣t(R)=R4。

（4）選定置信水平α∈[0,1]，構建α-截矩陣t(R)α,令α由1降至0，按t(R)α進行動態(tài)聚類：

①當0.998 6＜α≤0時，Ai(i=1,2,…,7)被分為7類：{A1},{A2},{A3},{A4},{A5},{A6},{A7}；

②當 0.992 1＜α≤0.998 6時，Ai(i=1,2,…,7)被分為6類：{A1},{A2,A3},{A4},{A5},{A6},{A7}；

③當 0.986 7＜α≤0.992 1時，Ai(i=1,2,…,7)被分為5類：{A1},{A2,A3},{A4,A6},{A5},{A7}；

④當 0.913 2＜α≤0.986 7時，Ai(i=1,2,…,7)被分為4類：{A1,A2,A3},{A4,A6},{A5},{A7}；

⑤當 0.752 7＜α≤0.913 2時，Ai(i=1,2,…,7)被分為3類：{A1,A2,A3},{A4,A6,A7},{A5}；

⑥當 0.576 9＜α≤0.752 7時，Ai(i=1,2,…,7)被分為2類：{A1,A2,A3},{A4,A5,A6,A7}；

⑦當0＜α≤0.576 9時，Ai(i=1,2,…,7)被分為1類：{A1,A2,A3,A4,A5,A6,A7}。

如果利用文獻[25]中猶豫模糊集的相關系數(shù)公式：

計算關聯(lián)矩陣C，得：

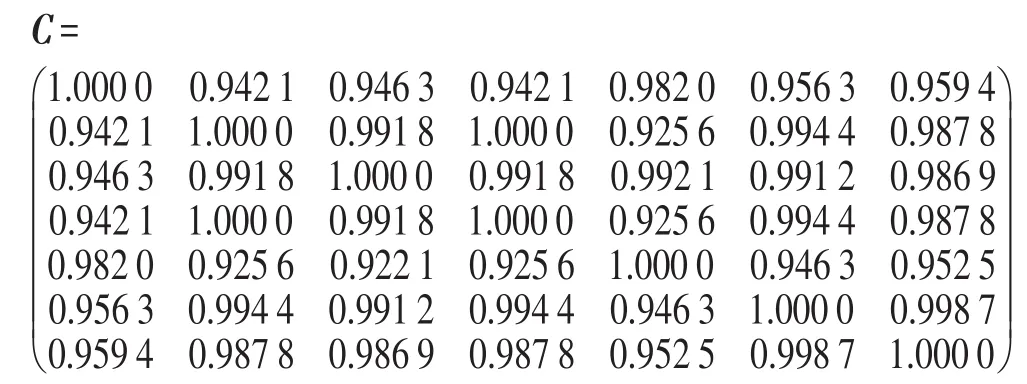
構造等價關聯(lián)矩陣，計算C2,C4,…,C2n,…，有C8=C4，即C4為一個等價關聯(lián)矩陣：

選擇不同的截割水平α∈[0,1]，建立C4的α-截矩陣，所得聚類結果如表4左側所示，文獻[33]和文獻[34]中的聚類方法得到的聚類結果見表4中側和右側。

通過比較可以發(fā)現(xiàn)，文獻[25]的聚類結果與本文主要有以下差別：（1）文獻[25]中的相關系數(shù)公式最多可將樣品分成6類，本文的協(xié)相關度公式所得結果則更加精細，可以滿足不同層次的需求。（2）聚類結果存在很大差異。在聚為6類時，文獻[25]把A2和A4歸為一類，事實上A2和A4更接近，有的屬性下甚至相等。在聚為5類時，文獻[25]把A6和A7歸為一類，而A4與A6更相似，因此本文將A2與A3，A4與A6作為一類更合理，這也與文獻[33]和文獻[34]所得結果一致。

Table 4 Comparison of various clustering results表4 各種聚類的結果比較

造成這些差異的原因在于構造相似矩陣時所用的計算猶豫模糊集相關程度的公式上，本文的協(xié)相關度公式是源于統(tǒng)計學中相關系數(shù)的構造思想，因此有一定的理論支撐，它比文獻[25]的相關系數(shù)公式復雜，這就保證了能充分利用決策矩陣中的數(shù)據(jù)，減少信息流失。此外，在計算論域里各元素的權重（屬性權重）時，本文提出的交叉熵距離表示的差異程度相對于其他距離公式有更高的分辨率，用它得出的權重公式更加合理，能客觀反映不同屬性的地位差別。而文獻[25]提出的方法需要權重矢量完全已知，沒有充分挖掘決策信息本身，其結果與實際情況有一定的偏差。

文獻[33]和文獻[34]所用的聚類方法得到的分類結果與本文也有所不同。劉小弟等人[24]指出，文獻[33]使用層次聚類法對猶豫模糊集進行聚類分析，利用最小距離作為聚類依據(jù)，一旦一組樣本被合并，就需要利用猶豫模糊平均算子在新生成的類上重新計算聚類中心，這種反復性的計算很繁瑣，而且平均算子的使用勢必會造成一部分的信息丟失，導致最后的結果不可靠；文獻[34]利用最小生成樹（minimum spanning tree，MST）算法得到聚類結果，它所使用的距離公式分辨率不夠高，且屬性權重帶有一定的主觀性，計算出的結果有時與事實有較大偏差，這必然會影響最后的聚類。

本文利用猶豫模糊信息的交叉熵作為距離，基于離差最大化方法獲得屬性權重，提出加權的協(xié)相關度公式，使用模糊等價聚類方法，借助于計算機軟件計算模糊等價矩陣，進而獲得聚類結果。相比于其他方法，該算法設計合理，操作過程程序化，便于計算機處理，易形成動態(tài)聚類，且能有效保留信息，使計算結果客觀可靠。

6 結束語

模糊集理論作為不確定理論中重要的一支，因能深刻真實地反映現(xiàn)實客觀世界與人們內心世界而被廣泛應用到運籌與管理、經(jīng)濟與決策各個領域，相繼出現(xiàn)了直覺模糊集、模糊軟集、區(qū)間型模糊集以及模糊數(shù)等推廣演變形式，它們構成了一個模糊理論體系，但這些理論對實際問題刻畫得不夠細致具體。在進行重大決策時經(jīng)常是多個決策者共同參與，這就勢必會出現(xiàn)意見不統(tǒng)一或者決策者自身就徘徊不定的情況，因此猶豫模糊集被提出。它是經(jīng)典模糊集的另一種推廣，其隸屬度允許一個或幾個可能的值，這樣就能全面描述人們的真實想法，且能避免使用各種算子來合成各個專家提供的數(shù)據(jù)，從而能直接處理它們，減少了信息的丟失。

聚類分析是數(shù)量統(tǒng)計中多元分析的一個分支，它是一種硬劃分，把每個待辨識的對象嚴格地劃分到某個類當中，具有非此即彼的性質，這種分類的類別界限是分明的。因為現(xiàn)實的分類往往伴隨著模糊性，所以用模糊理論來進行聚類分析會顯得更自然，更符合客觀實際[35]。目前模糊理論在聚類分析方面的應用已得到很大發(fā)展，但數(shù)據(jù)類型是猶豫模糊元的聚類分析還不多見。本文針對猶豫模糊環(huán)境下的聚類分析，提出猶豫模糊集的協(xié)相關度的概念，在獲取論域各元素的權重上，使用分辨率較高的交叉熵距離建立優(yōu)化模型得到，以確保加權的協(xié)相關度公式在計算不同猶豫模糊集的關聯(lián)程度時更加靈敏合理，構建的關聯(lián)矩陣更能體現(xiàn)不同對象的差異性。基于這些理論成果，最后給出了猶豫模糊信息下的聚類方法，并通過具體實例說明了所提聚類方法的可行性與有效性。

[1]Torra V,Narukawa Y.On hesitant fuzzy sets and decision[C]//Proceedings of the 18th IEEE International Conference on Fuzzy Systems,Jeju Island,Aug 20-24,2009.Piscataway:IEEE,2009:1378-1382.

[2]Torra V.Hesitant fuzzy sets[J].International Journal of Intelligent Systems,2010,25(6):529-539.

[3]Atanassov K T.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1):87-96.

[4]Dubois D,Prade H.Fuzzy sets and systems:theory and applications[M].Orlando:Academic Press,Inc,1980.

[5]Yager R R.On the theory of bags[J].International Journal of General Systems,1986,13(1):23-37.

[6]Xia Meimei,Xu Zeshui.Hesitant fuzzy information aggregation in decision making[J].International Journal of Approximate Reasoning,2011,52(3):395-407.

[7]Xia Meimei,Xu Zeshui,Chen N.Some hesitant fuzzy aggregation operators with their application in group decision making[J].Group Decision and Negotiation,2013,22(2):259-279.

[8]Xu Zeshui,Zhang Xiaolu.Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information[J].Knowledge-Based Systems,2013,52(6):53-64.

[9]Zhu Bin,Xu Zeshui,Xia Meimei.Dual hesitant fuzzy sets[J].Journal of Applied mathematics,2012.doi:10.1155/2012/879629.

[10]Zhu Bin,Xu Zeshui.Some results for dual hesitant fuzzy sets[J].Journal of Intelligent and Fuzzy Systems,2014,26(4):1657-1668.

[11]Xia Meimei,Xu Zeshui.Entropy/cross entropy-based group decision making under intuitionistic fuzzy environment[J].Information Fusion,2012,13(1):31-47.

[12]Liu Xuecheng.Entropy,distance measure and similarity measure of fuzzy sets and their relations[J].Fuzzy Sets Systems,1992,52(3):305-318.

[13]Zeng Wenyi,Li Hongxing.Relationship between similarity measure and entropy of interval-valued fuzzy sets[J].Fuzzy Sets Systems,2006,157(11):1477-1484.

[14]Zeng Wenyi,Guo Ping.Normalized distance,similarity measure,inclusion measure and entropy of interval-valued fuzzy sets and their relationship[J].Information Sciences,2008,178(5):1334-1342.

[15]Zhang Qiansheng,Jiang Shengyi.Relationships between entropy and similarity measure of interval-valued intuitionistic fuzzy sets[J].International Journal of Intelligent Systems,2010,25(11):1121-1140.

[16]Xu Zeshui,Xia Meimei.Hesitant fuzzy entropy and crossentropy and their use in multiattribute decision-making[J].International Journal of Intelligent Systems,2012,27(9):799-822.

[17]Gerstenkorn T,Manko J.Correlation of intuitionistic fuzzy sets[J].Fuzzy Set Systems,1991,44(1):39-43.

[18]Hong D H,Hwang S Y.Correlation of intuitionistic fuzzy sets in probability spaces[J].Fuzzy Set Systems,1995,75(1):77-81.

[19]Hung W L,Wu J W.Correlation of intuitionistic fuzzy sets by centroid method[J].Information Sciences,2002,144(1/4):219-225.

[20]Bustince H,Burillo P.Correlation of interval-valued intuitionistic fuzzy sets[J].Fuzzy Set Systems,1995,74(2):237-244.

[21]Hong D H.A note on correlation of interval-valued intuitionistic fuzzy sets[J].Fuzzy Set Systems,1998,95(1):113-117.

[22]Xu Zeshui,Xia Meimei.On distance and correlation measures of hesitant fuzzy information[J].International Journal of Intelligent Systems,2011,26(5):410-425.

[23]Xu Zeshui,Xia Meimei.Distance and similarity measures for hesitant fuzzy sets[J].Information Sciences,2011,181(11):2218-2138.

[24]Liu Xiaodi,Zhu Jianjun,Liu Sifeng.Similarity measure of hesitant fuzzy sets based on symmetric cross entropy and its application in clustering analysis[J].Control and Decision,2014,29(10):1816-1822.

[25]Chen Na,Xu Zeshui,Xia Meimei.Correlation coefficients of hesitant fuzzy sets and their applications to clustering analysis[J].Applied Mathematical Modeling,2013,37(4):2197-2211.

[26]Xu Zeshui.Intuitionistic fuzzy hierarchical clustering algo-rithms[J].Journal of Systems Engineering and Electronics,2009,20(1):90-97.

[27]Wang Zhong,Xu Zeshui,Liu Shousheng,et al.A netting clustering analysis method under intuitionistic fuzzy environment[J].Applied Soft Computing,2011,11(8):5558-5564.[28]Xu Zeshui,Chen Jian,Wu Junjie.Clustering algorithm for intuitionistic fuzzy sets[J].Information Sciences,2008,178(19):3775-3790.

[29]Hwang C,Rhee F C H.Uncertain fuzzy clustering:interval type-2 fuzzy approach to C-means[J].IEEE Transactionson Fuzzy Systems,2007,15(1):107-120.

[30]Yang M S,Lin D C.On similarity and inclusion measures between type-2 fuzzy sets with an application to clustering[J].Computers and Mathematical with Applications,2009,57(6):896-907.

[31]Xu Zeshui.Uncertain multiple attribute decision making[M].Beijing:Tsinghua University Press,2004.

[32]Shen Hengfan.Probability theory and mathematical statistics[M].Beijing:Higher Education Press,2011.

[33]Zhang Xiaolu,Xu Zeshui.Hesitant fuzzy agglomerative hierarchical clustering algorithms[J].International Journal of Systems Science,2015,46(3):562-576.

[34]Zhang Xiaolu,Xu Zeshui.A MST clustering analysis method under hesitant fuzzy environment[J].Control and Cybernetics,2012,41(3):645-666.

[35]Hu Baoqing.Fuzzy theory foundation[M].Wuhan:Wuhan University Press,2010.

附中文參考文獻:

[24]劉小弟,朱建軍,劉思峰.基于對稱交互熵的猶豫模糊信息相似度及聚類應用[J].控制與決策,2014,29(10):1816-1822.

[31]徐澤水.不確定多屬性決策方法及應用[M].北京:清華大學出版社,2004.

[32]沈恒范.概率論與數(shù)理統(tǒng)計教程[M].北京:高等教育出版社,2011.

[35]胡寶清.模糊理論基礎[M].武漢:武漢大學出版社,2010.