適應阻尼變化的車身高度控制系統

李仲興，于文浩

(江蘇大學 汽車與交通工程學院， 江蘇 鎮江 212013)

車身高度的主動控制是空氣懸架特有的優勢之一，較好地緩解了車輛在行駛過程中操縱穩定性和乘坐舒適性的矛盾。現今國內外的車身高度控制研究已經從經典控制領域(如PID控制、積分分離的PID控制等)向多模式切換控制、混雜控制、滑膜控制及神經網絡PID自適應控制等現代控制領域發展[1-6]。而隨著阻尼可變的半主動懸架應用日益廣泛，一些學者也對車身高度與阻尼的協同控制進行了探索。

在車身高度與阻尼的集成控制中，汪少華等[7]提出基于車身高度切換優先的車身高度和阻尼多模式切換控制，并仿真驗證了模式切換控制系統的有效性。陳一鍇等[8]根據車速和路面不平度確定車身高度，從阻尼與空氣彈簧剛度相匹配的角度出發協同控制車身高度與阻尼。趙景波等[9]提出一種主動懸架系統的高度與阻尼集成控制方法，并通過試驗驗證了不同車身高度和不同阻尼形式的組合對車輛性能的影響。

由此可見，現今車身高度與阻尼的協同控制研究主要集中在不同車身高度調節結果及阻尼狀態下的模式切換及匹配問題，未考慮在車身高度調節過程中阻尼系數的變化對車身高度調節品質的影響，對在阻尼系數變化下的車身高度調節動態特性缺乏一定的探索。而在車身高度與阻尼的相互協同控制中，除了應當獲取當前車身高度并據此對阻尼系數控制進行修正外，車身高度在調節過程中也應獲取當前的阻尼值并據此做出相應調整以保證車身高度調節過程的品質。為提高車身高度控制系統在調節過程中阻尼系數不停變化狀態下的控制效果，繼續完善車身高度與阻尼的相互協同控制，本文以在天棚阻尼控制策略控制下的懸架為例，建立空氣懸架車身高度控制系統模型，并提出適應阻尼變化的車身高度控制系統，建立并完善相應的離線專家庫模塊，并對控制效果予以分析。

1 空氣懸架車身高度控制系統建模與試驗驗證

空氣懸架車身高度控制是通過對空氣彈簧充放氣來實現的。結合變質量系統的熱力學過程和車輛動力學，可建立空氣懸架充放氣模型，并在此基礎上建立考慮阻尼系數變化的車身高度控制系統模型。空氣懸架充放氣系統主要由儲氣罐、電磁閥、管路及空氣彈簧等子系統構成[10-11]。

儲氣罐模型為

(1)

電磁閥模型為

(2)

式中：S為通過電磁閥的等效截面積；b為臨界壓力比；Pu為上游氣壓；Pd為下游氣壓。充氣時，上游氣壓為儲氣罐內部氣壓，下游氣壓為空氣彈簧氣壓；放氣時，上游氣壓為空氣彈簧氣壓，下游氣壓為大氣壓。

管路模型為

(3)

式中：L為互聯管長；Td為互聯管路末端溫度；Rt為互聯管路阻力系數；c為聲速，25 ℃時取 346 m/s。

空氣彈簧模型為

(4)

車輛動力學模型：

(5)

式中：

(6)

其中：Mb為簧載質量；Zb為簧載質心的垂向位移；Bf、Br分別為前后車輪輪距；a、b分別為簧載質量質心到前后軸處的距離；Ir、Ip分別為簧載質量繞X、Y軸的轉動慣量；θ、Φ分別為簧載質量側傾角與俯仰角；Fi(i=1,2,3,4，分別對應前左、前右、后左、后右懸架)為懸架作用于車身的懸架力；Pi、Pa分別為4個空氣彈簧實際氣壓與初始氣壓；Aei為4個空氣彈簧的有效面積；c為減震器阻尼系數；fdi為4個懸架動行程；Kθgf、Kθgr分別為前后橫向穩定桿的側傾角剛度；Mt為車輪質量；Kt為車輪等效垂向剛度；Zti為4個車輪垂向位移；qi為作用于4個車輪的路面垂向激勵。

同時，為確保在車身高度控制過程中阻尼系數能根據舒適性需求進行改變，除在模型中添加阻尼系數可變的阻尼減震器及考慮其線性化外，模型還需引入一種阻尼控制策略。天棚阻尼控制是經典的阻尼系數控制邏輯，其算法簡單、易于實現，且魯棒性強[12]。因此，本文選擇天棚阻尼控制為阻尼控制策略，其控制律如下：

(7)

式中：Cin(t)為減振器實際阻尼系數；Cmax為減振器所能提供的最大阻尼系數；Cmin為減振器所能提供的最小阻尼系數。

PID控制器具有原理簡單、穩定性好、易于實現等優點，被廣泛應用于工程實際，其算式如下：

(8)

其中：e(t)為目標值與實際值之差；KP、TI、TD分別對應比例系數、積分時間系數以及微分時間系數。

在車身高度調節時，通過PID控制器輸出量無法直接實現對氣體質量流量的無極可調，因此采用PWM占空比輸出的方法控制電磁閥充放氣，實現充放氣時氣體質量流量的大小控制。

基于Matlab/Simulink環境根據式(7)(8)建立仿真模型，同時為驗證仿真模型的準確性，基于MTS-320四通道液壓伺服激振臺建立空氣彈簧車身高度控制試驗平臺，如圖1所示。

所用樣車基于某轎車底盤改裝而成。試驗樣車車身被拆除,并用一塊具有多個凹槽的鋼板取代，凹槽用于放入沙袋、試驗假人等，便于靈活配置簧上質量。試驗臺架布置有4個空氣彈簧高度傳感器用以采集當前車身高度信息。4個充氣電磁閥、4個放氣電磁閥分別控制懸架前軸和后軸4個空氣彈簧的充放氣。阻尼器采用兩級可調阻尼減震器。電磁閥及阻尼器由型號為MPC565的ECU控制。

圖1 空氣懸架車身高度調節試驗平臺

表1 樣車參數

由于MTS-320四通道液壓伺服激振臺產生的路面激勵難以與仿真中的路面相一致，因此采用路面激勵為0的靜態車身高度調節過程來驗證仿真模型的準確性。在仿真與試驗中采用相同的車身高度控制參數，在車輛各懸架阻尼所有組合狀態下以抬升和降低車身高度20 mm為目標進行仿真與試驗的結果對比。

考慮到前后懸架有較多參數不相同，在相同控制參數下以前后懸架的高度控制對比難以體現阻尼變化對車身姿態的影響。現以懸架阻尼“同為硬”和“左側為軟、右側為硬”兩種狀態，以抬升車身高度20 mm為目標，舉例說明仿真與試驗對比結果。仿真與試驗結果如圖2所示。

圖2 車身高度調節仿真與試驗對比

由圖2可知：在靜態車身高度調節過程中，仿真結果與試驗結果吻合度較好，證明了仿真模型是準確可靠的，以下研究將依托此模型開展。

2 適應阻尼變化的車身高度控制系統的建立

在行車過程中，車身高度應隨車速、路面等條件進行適當調整，以滿足車輛對行駛平順性和操縱穩定性的需求。而在車身高度調節過程中，懸架的阻尼系數大小仍然受阻尼控制策略控制不停改變。阻尼系數的變化將直接影響車身高度調節系統中阻尼比的大小，此時若保持控制參數不變，則難以滿足阻尼系數改變后車身高度調節系統的控制品質要求，進而對車身高度調節時間和超調等時域品質產生較大影響，導致車身高度調節過程中車身姿態較差。前期的仿真及試驗研究結果也驗證了這一現象。

為進一步削弱在車身高度調節過程中因阻尼系數變化而帶來的車身姿態問題，本文提出如圖3所示的適應阻尼變化的車身高度控制系統。

圖3 適應阻尼變化的車身高度控制系統框圖

該車身高度控制系統分為離線和在線兩個部分。在離線部分中，在車輛4支懸架阻尼器所能產生的所有阻尼系數組合下對車身高度調節的控制參數進行尋優。尋優目標除了傳統的車身高度調節的目標外，還應將車身俯仰與側傾程度考慮進去。最后通過優化結果建立離線專家系統。在線部分與傳統車身高度調節相比添加了控制參數切換系統。在車輛行駛過程中阻尼控制器不停產生阻尼系數控制信號，此時控制參數切換系統讀取該控制信號，依此提取離線專家系統中與當前阻尼狀態對應的最優控制參數，并立即寫入車身高度控制器，再由車身高度控制器根據寫入的最優控制參數進行車身高度調節。

3 最優控制參數尋優及專家系統的建立

3.1 應用遺傳算法的控制參數尋優

遺傳算法GA(genetic algorithms,GA)是模擬生物在自然環境中的遺傳和進化過程而形成的一種全局優化概率搜索算法。遺傳算法無需對目標函數微分，可提高參數優化水平，簡化優化的解析計算過程[13-15]。遺傳算法主要過程及參數設置如下：

1) 編碼

遺傳算法中的選擇、交叉和變異操作都是針對個體染色體而言，原始的參數集合無法直接完成上述3種操作，所以必須對參數集合進行編碼以得到個體染色體。整車車身高度調節PID控制參數共有12個，由于參數較多以及為避免二進制編碼中的hamming懸崖問題，本文選擇實數編碼方式。

2) 適應度函數

傳統基于遺傳算法的PID參數整定一般利用誤差積分指標作為系統整定的性能指標[15]，以保證車身高度控制的時域響應。而作為整車的車身高度控制，還應將車身側傾及俯仰指標考慮在內,以保證車身高度調節過程中的車身姿態穩定。同時應注意,與靜態車身高度調節不同的是，在行車過程中，車輛受路面激勵，作為反饋信息來源的懸架動行程此時是一個理想車身高度值與一個與路面激勵有關的噪聲的和。而在路面激勵下，懸架的動行程在統計規律上是服從正態分布的，因此在仿真尋優過程中，可讓整車模型在較多數量的路面上運行，最后取每個懸架動行程的期望作為預期的車身高度信息，并以此來評價對應的控制參數在車輛行駛過程中車身高度調節的品質。

評價參數共有4個：

(9)

(10)

(11)

(12)

其中：Eh為車身高度誤差對時間的積分；Er為車身側傾角絕對值對時間的積分；Ep為車身俯仰角絕對值對時間的積分；ce為超調幅值；t為仿真時間；Aim為目標車身高度；Rh(t)為懸架動行程；Rr(t)為車身側傾角；Rp(t)為車身俯仰角；i取值1、2、3、4，即n=4，分別代表前左、前右、后左和后右4個懸架；j代表仿真的路面；m此處取100。

遺傳算法的個體適應度函數表示為

(13)

其中：F為個體適應度值；ω1、ω2和ω3為權重系數；Eh決定車身高度調節的誤差及時間，其權重越大則調節時間越短，但會產生較大的超調；ce決定車身高度調節的超調幅值，與Eh相互制衡，其權重越大則調節時間越久，但調節結果會有較大誤差；Er與Ep決定各懸架處的車身高度調節同步程度，權重越大則調節同步程度越高。

3) 選擇操作

采用比例選擇算子與最優保存策略相結合的方法進行選擇操作是最為常用的方法。首先保存每一代中適應度最好的個體，使其不參與交叉和變異運算，直接復制到下一代群體，然后根據個體適應度占當代所有個體適應度和的比例確定剩余個體被選概率，則第i個個體的選擇概率為

(14)

式中：Fi為第i個個體適應度值；M為種群大小，此處取80。

4) 交叉操作

交叉操作是不同染色體同一位置基因相互交換的過程。假設利用交叉概率pc判斷后，確定讓第i個染色體ai和第j個染色體aj在第l至第n位基因發生交叉操作，則交換過程為：

(15)

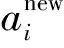
5) 變異操作

選擇第i個個體的第l位基因ail進行變異，操作方法如下：

(16)

其中：f為(0,1)范圍內的隨機數；r為變異取值半徑。

3.2 不同阻尼組合下控制參數的尋優結果

遺傳算法其他參數設置為：遺傳代數為100；交叉概率pc=0.6；變異概率pm=0.01。經過初步試驗，取4懸架處車身高度控制參數初始范圍都為：Kp=0～30，Ki=0～10，Kd=0～50。由于篇幅限制，以前左懸架的車身高度調節的尋優結果為例分析，如表2所示。其中：當阻尼器狀態為“軟”時，其壓縮阻尼系數為1 800 N·(s·m-1)，拉伸阻尼系數為2 800 N·(s·m-1)；當阻尼器狀態為“硬”時，其壓縮阻尼系數為4 600 N·(s·m-1)，拉伸阻尼系數為9 460 N·(s·m-1)。

表2 前左懸架車身高度調節參數尋優結果

3.3 離線專家系統的建立

根據現有尋優結果，在基于本文建立的經過試驗驗證的模型的基礎上添加離線專家系統和控制參數切換系統。以Kp參數的離線專家系統和控制參數系統為例，系統界面如圖4所示。

圖4 離線專家系統和控制參數系統

圖4中： “各懸架阻尼系數”模塊中damp值為阻尼控制器的輸出，包含4個懸架處的阻尼控制信息，當其為1時代表當前阻尼器為“軟”狀態，當其為4時代表當前阻尼器為“硬”狀態。在系統運行過程中，當阻尼控制器產生相應的輸出時，控制參數切換系統能依據其切換規則，在離線專家庫中選擇當前對應的控制參數矩陣并輸出。

4 控制系統響應與控制效果分析

4.1 靜態車身高度調節對比分析

為分析所建立的適應阻尼變化的車身高度控制系統在不同阻尼狀態下的響應及表現，通過控制變量讓車輛處于靜止狀態，再觀察阻尼系數變化下的靜態車身高度調節品質。建立如圖5所示的阻尼控制信息變化規律。分別在第1、2、3和4 s時，讓前左、前右、后左和后右懸架阻尼控制信息從1變為4。

圖5 阻尼系數隨時間的變化

將16組尋優結果的控制參數分別代入到在該阻尼控制信息變化下的傳統車身高度控制模型中，尋找出最優一組控制參數，并以此組控制參數作為參照，仿真分析在靜態時阻尼系數變化下傳統車身高度控制與適應阻尼變化的車身高度控制的控制效果及品質，結果如圖6、7所示。仿真結果表明：在阻尼系數變化下的靜態車身高度控制中，適應阻尼變化的車身高度控制的調節時間、超調量及誤差較傳統車身高度控制更優。車身高度調節過程中的波動可能是由于遺傳代數的限制所得的尋優結果并未收斂到最優值的原因，但并不影響結論的正確性。

圖6 不同車身高度控制系統在調節過程中阻尼系數發生變化時的表現

圖7 不同車身高度控制系統在調節過程中阻尼系數發生變化時車身側傾角變化

4.2 動態車身高度調節對比分析

由于阻尼系數變化受天棚阻尼控制，車輛在靜止時阻尼系數一般會保持不變。因此，利用白噪聲生成法建立路面模型，輸入到整車模型中，同時阻尼器系數由天棚控制器控制。仿真在車速為72 km/h、多種A級路面、升高車身高度20 mm的條件下進行，車身高度調節結果取每次仿真的均值表示，歷次仿真結果及其均值如圖8、9所示。

圖8 天棚阻尼控制下不同系統的動態車身高度調節過程

圖9 天棚阻尼控制下不同系統的動態車身高度調節車身側傾角變化

圖8、圖9表明：在仿真條件下，采用適用阻尼變化的車身高度控制的調節時間比傳統的車身高度調節時間縮短了7.1%，超調量減小了9.2%；兩者的車身側傾角大多在平衡位置上下波動且幅值較小，但在適用阻尼變化的車身高度控制下，車身側傾角離平衡位置更近。

5 結束語

本文根據阻尼對車身高度控制影響的前期研究，提出適應阻尼變化的車身高度控制系統，通過獲取當前車輛的阻尼控制輸出的阻尼控制信息調整車身高度控制的控制參數，從而保證在阻尼變化過程中車身高度控制參數始終為最優控制參數。同時，利用經試驗驗證的靜態整車車身高度控制模型，添加路面激勵及阻尼控制器模塊，構建動態整車車身高度控制模型。通過遺傳算法尋優獲得在不同阻尼參數組合下的最優動態車身高度控制參數，并完善所提出的適應阻尼變化的車身高度控制系統的離線專家系統。

仿真結果表明：在阻尼變化的靜態車身高度控制過程中，適應阻尼變化的車身高度控制系統在阻尼系數變化時能很好地適應工況的變化提高車身高度控制品質，同時車身高度變化平穩，未發生斷點、跳躍等現象；在動態車身高度控制中，適應阻尼變化的車身高度控制系統調節快速平穩、超調量小、車身姿態控制較好，其調節品質相對于傳統車身高度控制策略有著較大的提升。

參考文獻：

[1] KIM H,LEE H.Height and leveling control of automotive air suspension system using sliding mode approach[J].IEEE Transactions on Vehicular Technology,2011,60(5):2027-2041.

[2] 潘公宇,候觀遠青.基于車身高度控制的主動液壓懸架建模與仿真[J].重慶理工大學學報(自然科學),2016， 30(11)：1-6.

[3] HUANG T,CHEN G,ZONG C,et al.Research on Vehicle Height Adjustment Control of Electronically Controlled Air Suspension[R].USA:SAE Technical Paper,2015.

[4] 李仲興,于文浩.阻尼對車身高度控制效果的影響分析[J].重慶理工大學學報(自然科學),2016,30(4):11-15.

[5] SUN X Q,CAI Y F,YUAN C C,et al.Vehicle height and leveling control of electronically controlled air suspension using mixed logical dynamical approach[J].Science China Technological Sciences,2016,59(12):1814-1824.

[6] SUN X,CAI Y,CHEN L,et al.Vehicle height and posture control of the electronic air suspension system using the hybrid system approach[J].Vehicle System Dynamics,2016,54(3):328-352.

[7] 汪少華,陳龍,孫曉強.半主動空氣懸架多模式切換控制模型的分析[J].江蘇大學學報 (自然科學版),2013 (6):637-642.

[8] CHEN Yikai,HE Jie.Stiffness-damping matching method of an ECAS system based on LQG control[J].Journal of Central South University,2014,21(1):439-446.

[9] 趙景波,倪彰,貝紹軼.電動化底盤主動懸架系統高度與阻尼集成控制[J].廣西大學學報,2015,40(2)：347-356.

[10] TESFAY A H,GOEL V K.Analysis of semi-active vehicle suspension system using airspring and MR damper[C]//IOP Conference Series:Materials Science and Engineering.USA:IOP Publishing,2015:012020.

[11] 徐興.ECAS 客車車身高度非線性系統控制的研究[D].鎮江：江蘇大學,2010.

[12] SUGAHARA Y,KOJIMA T,AKAMI Y,et al.Development of a vertical semi-active suspension system using variable hydraulic dampers[J].WIT Transactions on The Built Environment,2016,162:469-477.

[13] 郝輝,李雪瑞,李亞雄.基于遺傳算法的面目標瞄準點尋優問題研究[J].兵器裝備工程學報,2016,37(1):128-131.

[14] 蔣廷利,李靜,魏強.基于遺傳優化與矢量擬合的濾波器參數提取[J].壓電與聲光,2015,37(4):701-706.

[15] DEB K,SINDHYA K,HAKANEN J.Decision Sciences:Theory and Practice:Multi-objective optimization[M].New York:CRC Press,2016:145-184.