一個新四翼憶阻混沌系統的設計與性能分析

雷宇

摘要

將一個基于雙曲函數的非線性函數應用于三次磁控憶阻混沌系統得到一個四翼吸引子混沌系統，通過吸引子相圖、lyapunov指數分析表明，該多翼混沌吸引子具有更豐富，更復雜的動力學特征，仿真結果和理論計算一致，為新的混沌電路的設計提供了一種思路。

【關鍵詞】連續非線性函數 憶阻混沌系統 混沌吸引子 lyapunov指數

1982年，蔡少棠提出了著名的蔡氏電路，在一定參數條件下，可產生各種分岔、單渦卷和雙渦卷混沌吸引子等非線性現象和混沌動力學行為[1-2]。Itoh和蔡少棠[3]利用一個分段線性的憶阻器替換蔡氏混沌電路中的蔡氏二極管，得到第一個憶阻混沌振蕩路。Muthuswamy[4]將一個不連續分段線性憶阻器代替蔡氏電路中的二極管，得到新的混沌行為。

包伯成基于一個具有光滑連續的三次單調上升的磁控憶阻器設計出憶阻混沌電路，具有豐富而獨特的動力學特性[5-6]。自1993年suyken等成功構造多渦卷系統后，許多學者分別采用分段線性函數、時滯函數、正弦函數和飽和函數[7-10]在Lorenz系統[11-13]、Jer[14]、colpitts[15]等不同混沌系統構建了更為復雜的多渦卷吸引子，被廣泛的應用于保密通訊、信息加密、數字語音等信息領域，這種獲得更為復雜的混沌吸引子的方式也日益被關注。

本文設計了一個基于雙曲函數的連續非線性函數，將此函數應用于三次光滑憶阻混沌系統，對新系統進行動力學分析，并對其進行matlab仿真仿真，結果與數值計算結果一致。2新的四翼憶阻混沌系統的設計

（1）包伯成構建的光滑憶阻混沌系統的動力學方程為：

x=A[y-x+Dx-W（w）x]

y=x-y+z

z=-By-Cz

w-x

W（w）憶阻器憶導，W（w）=a+3bw2，式（1）中：x，y，z，w為狀態變量，A，B，C，D，a，b為系統參數。當選擇參數A=16.4，B=15，c=o.5，D=1.4，a=0.2，b=0.4時，系統（1）存在一個典型的兩渦卷混沌吸引子，如圖1所示。

（2）構建一個基于雙曲函數的非線性函數，表達式為：

F=k*z-p*k*（-tanh（n*z）+tanh（n*z）+tanh（n*（z+2 *p》+tanh（n*z）+tanh（n*z-2 *p》

此函數由線性函數和非線性函數合成，是連續的，k分別為0 65和0 35時非線性函數F（z）的曲線圖如圖2所示，由圖1可知，k可改變非線性函數的斜率。

（3）將非線性函數引入到系統（1）第4式，從而構建了如下的新的憶阻混沌系統（2）：

x=A[y-x+Dx-W（w）x]

y =x-y+z

z=-By-Cz

w=x+k+z—p*k*（-tanh（n*z）+tanh（n*z）+tanh（n*（z+2*p》）+tanh（n*z）+tanh（n*z-2*p》

3新系統的動力學分析

3.1對稱性

新系統作變換（x，y，z，w）一（-x，-y，-z，-w），系統保持不變，即系統關于原點對稱，這種對稱性，對于所有參數都成立。

3.2耗散性

散度

vv=

此時系統是耗散的，當在此條件下，當t趨近于無窮大時，系統軌線上每一個小體積元收斂到零，系統的軌道逐漸趨于一個吸引子。

3.3混沌吸引子，lyapunov指數和維數

設新混沌系統初始值為（O.l，0.1，O.l，O.l），在matlab中應用龍格.庫塔法進行數值計算可以得到吸引子相圖，利用wolf方法可以得到李雅普諾夫指數。

固定，時間步長為0.5，最大時長為400，新系統混沌吸引子如圖所示，由圖可看出：相比單向兩渦卷混沌系統相比，該系統在多方向上分離產生四翼吸引子，具有更復雜的動力學行為。

3.3.1固定P=5，n=30，k=0.95

設時間步長為0 5，最大時長為400，新系統混沌吸引子如圖3所示，由圖可看出：相比單向兩渦卷混沌系統，新系統相軌在更多方向上分離，在不同方向拉伸折疊變換，產生四翼吸引子。當初始值為（0.1，O.l，O.l，O.l），時間步長為0 5，最大時長為400，李雅譜諾夫指數為LEl=0.104657，LE2=0，LE3=-0 851344，LE4=-19.664244，系統的維數為：

Ei= 2.0051，系統lyapunov指數一個為正，一個為O，兩個為負，且lyapunov維數是分數，因此系統在此參數下是混沌的。

3.3.2固定P=5，n=3，k=0.4

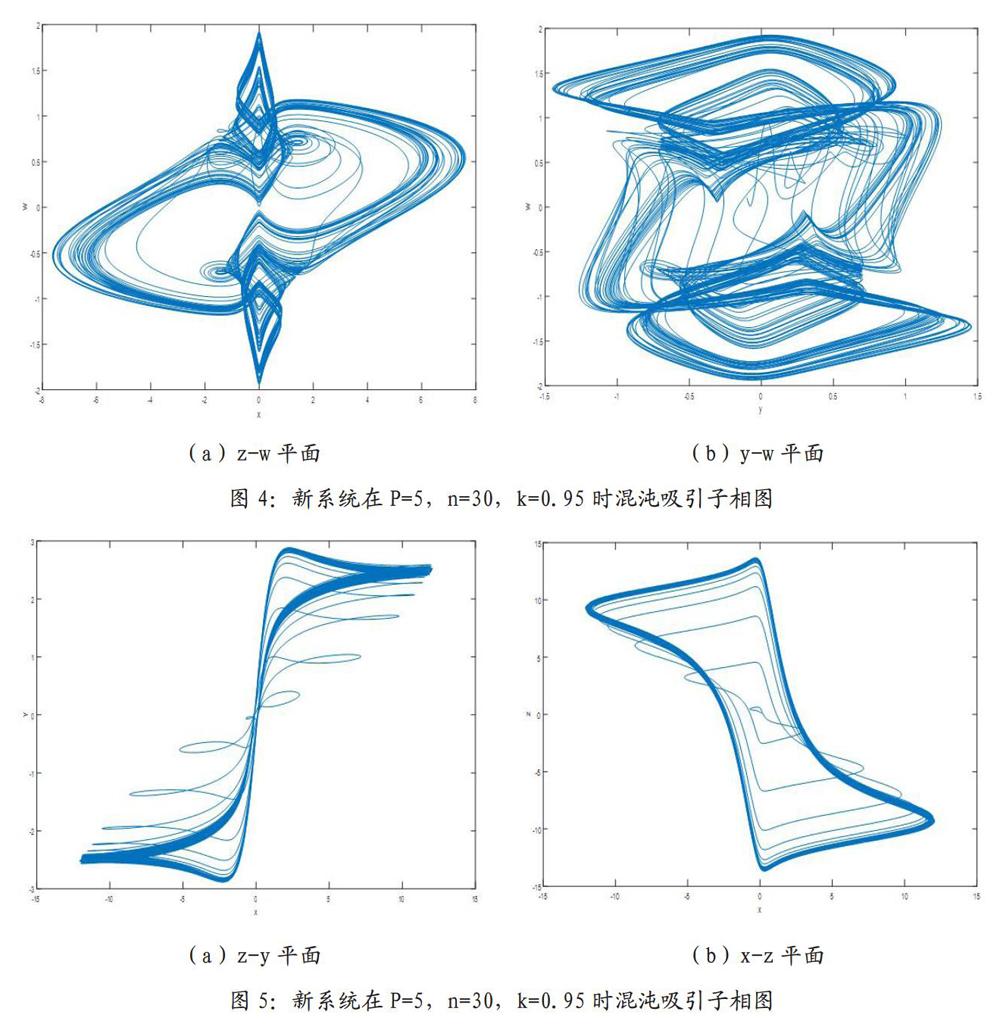
新系統的混沌吸引子如圖所示4。新系統相軌同樣產生四翼吸引子，但吸引子在x和方向收縮。當初始值為（O.1，O.l，O.l，O.l），時間步長為0.5，最大時長為400，李雅譜諾夫指數為LEl=0.167547，LE2=0，LE3=-0.792802，LE4=-17.720023，系統的維數為2 0092，系統lyapunov最大正指數相比參數為P=5，n=3，k=0.95時的狀態更大，且lyapunov維數是分數更大，因此系統在此參數下是混沌復雜度增大。

3.3.3固定P=5，n=30，k=-0.2

新系統的混沌吸引子如圖5所示。新系統以周期軌道運行。當初始值為（O.l，O.l，O.l，O.l），時間步長為0 5，最大時長為1200，新系統李雅譜諾夫指數為LEl=-0.072336，LE2=-0.131838， LE3=-0.331302， LE4=-26.192317，新系統lyapunov指數一個為O，三個為負值，可以說明系統處于周期態。

4結語

本文在一個二翼憶阻混沌系統的基礎上提出了一個新四翼混沌系統，利用理論分析和matlab數值計算分析了新系統，其既能產生不同形狀的四翼吸引子，也能得到周期性軌道，具有更加豐富的動力特征。為獲得新的混沌系統提供一種思路，在保密通信中的信息加密具有較高的應用價值，為在通訊安全領域的應用提供可行性依據。

參考文獻

[l]Chua L O， Komyro M， Matsumoto T.The Double Scroll Familiy[J].IEEE Transactions on Circuits andSys tems，

1986， 33 （11）： 1072-1118.

[2]Chua L O， Lin G N. CanonicalR ealization of Chua' s CircuitFamily [J]. IEEE Transactions onCircuits and Systems， 1990， 37 （7）： 885-902.

[3]1toh M， Chua LO. Memristoroscillators [J]. Int J Bifur Chaos，18： 3183-3206.

[4]Muthuswamy， B， and Kokate， PP.Memristor-Based Chaotic Circuits [J].IETE Tech.

Rev.，

2009， 26 （6）： 417-429.

[5]包伯成，胡文，許建平，劉中，鄒凌，憶阻混沌電路的分析與實現[J].物理學報，2011， 60 （12）：120502.

[6]包伯成，劉中，許建平，憶阻混沌振蕩器的動力學分析[J].物理學報，2010， 59 （06）： 378509.

[7] Yuan Fang， Wang Guangyi， WangXiaowei. Extreme multistabilityin a memristor-based multi-scrollhyperchaotic system[J]. Chaos，2016，2 6 （7）：1-10.

[8] Henry Alombah N， HilaireFotsin，MegamNgouonkadi E B， et al. Dynamics，analysis and implementation ofamultiscrollmemristor-basedchaotic circuit [J]. InternationalJournal of Bifurcation and Chaos，2016，26 （8）：1650128：1-20.

[9]Hu Xiaoyu， Liu Chongxin， Liu Ling， etal.

Mult i-scroll

hidden attractorsin improved sprott a system[J].Nonlinear Dynamics，

2016， 86 （3）： 1725-1734.

[10] Sajadjafari， Viet-Thanh Pham，Tomasz Kapitaniak. Multiscrollchaotic sea obtained from a simple3D system without equilibrium[J].International Journal of Bifurcationand Chaos， 2016， 26 （2）： 1-7.

[11]艾星星，孫克輝，賀少波.不同類型混沌吸引子的復合[J].物理學報，2014， 63 （04）： 040503.

[12]孫克輝，傅元理，簡化Lorenz系統多翅膀混沌吸引子的設計與電路實現[J].動力學與控制學報，2016，14 （05）： 395-400.

[13]艾星星，孫克輝，賀少波，王會海，簡化Lorenz多渦卷混沌吸引子的設計與應用[J].物理學報，2014，6 3 （12）：120511.

[14]王雅麗，李志軍等，電流型網格多渦卷混沌電路的設計與實現[J].微電子學，2017， 47 （02）： 226-232.

[15]王振宇，蘇詠梅，一種網格多渦卷混沌Colpitts振蕩器及其電路實現[J].電子器件.2017，40（06）：1441-1444.