退休年齡“固化”對生命周期“三階段”發展的影響

梁志偉 黃健元

(河海大學理學院，江蘇 南京 211100)

退休年齡“固化”是指現行法定退休年齡并沒有隨著社會經濟的發展及人口結構的改變而做出相應的調整。我國現行的法定退休年齡為：男職工60歲、女干部55歲、女工人50歲。另外，對于特殊行業的工作人員，退休年齡可以提前或者延遲。

為了應對人口老齡化帶來的養老保險基金支付壓力及勞動力短缺之困，西方主要發達國家紛紛采取延遲退休年齡政策。例如，德國政府決定從2012年開始延遲退休年齡，到2030年把退休年齡延長到67歲。英國決定從2016年4月開始逐步將女職工的退休年齡提高到65歲。我國是否需要延遲法定退休年齡，學術界對此并沒有統一結論。國內贊成或者反對延遲退休年齡的觀點主要集中于它是否可以減輕養老金支付的壓力及是否對就業產生影響。鄧大松等〔1〕認為退休年齡的延遲能夠緩解養老保險基金支付壓力，通過對退休年齡的敏感性分析，得出隨著退休年齡的提高幅度不斷增大，基金缺口規模不斷縮小的結論。鄭功成〔2〕認為，延遲退休年齡是為了更好地維護代際間的公平，保證養老金的延續。袁磊〔3〕認為延遲退休可以使得養老保險基金收不抵支的到來時間向后推遲，但并不能解決養老保險資金缺口問題。張車偉等〔4〕認為延遲退休對總體就業并不一定有不利影響，但對大學生的就業會有比較大的負面影響。蔡昉〔5〕認為單方面延遲法定退休年齡，而勞動力市場不能很好地吸收這些人口的話，就會使得這部分人陷入嚴重困境。唐鈞〔6〕認為，我國與歐美國家的國情不同，面對是否需要“延遲退休”，應該采取十分謹慎的態度。

韓克慶〔7〕指出目前延遲退休年齡所要解決的核心問題還不是很清楚，這也是民眾對此項政策的反對意見明顯多于贊成意見的重要原因之一。本文根據生命周期理論將人的一生劃分為三個階段來研究退休年齡“固化”對生命周期發展的影響，根據生命周期劃分情況采用相關方法預測生命周期發展趨勢。

1 分析原理及方法

1.1生命周期三階段的劃分 生命周期假說認為：人們是站在整個一生的高度來安排資源，將一生的總消費均勻地分配于生命周期的每一個階段。如果從工作年限和退休生涯兩方面考慮來追求整個生命周期效用最大化，則應在工作年限內為退休生涯的消費而儲蓄，使得各期的消費水平趨于相對穩定。根據出生、開始工作、退休、死亡四個時點將人的一生行為劃分為三個階段。第一階段為出生到開始工作，這一階段主要是受教育階段。第二階段為開始工作到退休，為工作階段，考慮到我國相關法律對最低工作年齡和退休年齡均有明確規定，同時為避免與“工作年限”等概念產生混淆，將“工作起始年齡到退休年齡的年限”界定為“法定工作年限”，其時間長度等于法定退休年齡減去工作起始年齡。相對于一般工作年限，法定工作年限強調擁有必要的工作年限是法律賦予每個人的權利。第三階段為退休到死亡，這一階段為退休階段。

1.2退休年齡“固化”對生命周期“三階段”發展的影響機制 退休年齡“固化”對生命周期“三階段”發展的影響主要是指退休年齡“固化”對生命周期三個階段的時間長度及占整個生命周期比例的影響。生命周期第一階段的時間長度為平均工作起始年齡；第二階段的時間長度為平均退休年齡減去平均工作起始年齡；第三階段的時間長度為平均預期壽命減去平均退休年齡。生命周期三階段的占比為各個階段的時間長度占整個生命周期的比例。與平均退休年齡和平均預期壽命不同，平均工作起始年齡與受教育年限密切相關，即平均工作起始年齡是在平均受教育年限的基礎上進行計算的。平均受教育年限的測算公式為：

(1)

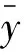
由于退休年齡是第二階段和第三階段的分水嶺，所以退休年齡“固化”主要影響的是第二階段和第三階段。從時間長度來看，隨著社會經濟的發展，教育投入的提高，平均受教育年限不斷增加，導致工作起始年齡提高。退休年齡“固化”使得出生到退休這一段時間也就是第一階段和第二階段時間長度之和保持不變。在退休年齡“固化”的情況下，工作起始年齡的提高必然壓縮法定工作年限。也就是說第一階段時間長度的增加必然導致第二階段的時間長度相應地減少。在退休年齡“固化”的情況下，隨著平均預期壽命的提高，退休階段的時間長度不斷增加。從占整個生命周期的比例來看，退休年齡“固化”影響最為嚴重的是法定工作年限的占比在工作起始年齡及預期壽命提高的合力下減少得更為顯著。這是因為一方面法定工作年限不斷縮短，另一方面整個生命周期長度不斷增加。

1.3生命周期發展趨勢預測方法

1.3.1平均工作起始年齡的預測方法 由于制定延遲退休年齡政策時要充分考慮未來幾十年生命周期發展情況，根據生命周期的劃分情況可知對生命周期“三階段”發展趨勢的預測就是對平均工作起始年齡及平均預期壽命進行預測。灰色理論用于研究樣本數據量很少的不確定性系統問題〔8〕。其中，灰色預測GM(1,1)模型在實際應用中較為廣泛。鑒于平均工作起始年齡的數據量較少，故而采用GM(1,1)模型。

設非負的原始序列為y(0)，經累加的數據序列為y(1)，則y(1)滿足一階微分方程：

(2)

其中：α為發展系數，μ為灰色作用量。這兩個參數的估計可由最小二乘法得到。

解方程(2)可以得到：

(3)

累減后得到原始數據序列的預測公式：

(4)

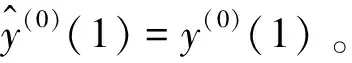
由于數據序列太短(4～5個)，要想進行長期預測會比較困難。這樣GM(1,1)模型的預測效果會大打折扣。針對這種情況，可以考慮“等維遞補灰色預測法”。該模型的主要過程是：根據初始數列利用GM(1,1)模型得到第一個預測值，將其補充在初始數列之后，然后去除初始數列的第一個數據，這樣就保持了數據序列的維數不變，然后根據新得到的數據序列再建立GM(1,1)模型，以此來預測下一個值，重復上述過程，直到完成預測目的或者是滿足精度標準為止。該方法相對于GM(1,1)來說，能夠補充和利用新的預測值，使得預測值在動態之中不斷產生，因此預測效果會更加理想。

1.3.2平均預期壽命的預測方法 預測平均預期壽命首先要預測全年齡段人口死亡率，然后通過編制生命表得到。Lee-Carter模型在實際應用中較為成熟，且能夠較好地反映死亡率的變動趨勢〔9〕。

Lee-Carter模型通過引入3個參數ax、βx和kt，將年齡別死亡率的變化分解為不隨時間變化的年齡因子和隨時間變化的年份因子兩部分。具體形式為：

ln(mx(t))=ax+βxkt+εx,t

(5)

其中，mx(t)表示第t年年齡為x歲的人的中心死亡率。參數ax表示年齡為x歲的人口死亡率取對數后的平均值；參數βx表示x歲死亡率隨時間變化的系數；參數kt表示第t年的死亡率水平；εx,t是模型誤差項，且εx,t～N(0,σ2)。為了使得參數估計能夠得到唯一解，同時進行以下規定：

∑xβx=1，∑tkt=0

(6)

(7)

使用最小二乘法求解Lee-Carter模型的另外兩個參數βx和kt，可以得到：

(8)

(9)

經典的Lee-Carter模型需要較多年份的死亡率數據才能對kt進行較好的預測。由于分年齡死亡率的數據較少，于是對kt的預測采用有限數據下的Lee-Carter模型〔10〕。

第一步，計算第t年、年齡為x歲的人在[x,x+1)歲之間的條件死亡概率(qx,t)，相應計算公式為：

(10)

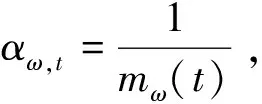
第二步，假設l0,t=100 000，計算第t年、年齡為x歲的尚存人數(lx,t)和[x,x+1)歲之間的死亡人數(dx,t)，相應迭代計算公式為：

(11)

第三步，計算第t年、年齡為x歲的人在[x,x+1)歲之間的平均生存人年數(Lx,t)。由于人口生命過程特征在不同年齡段上的差異，計算公式亦應有所區別。其分別為：

(12)

(13)

(14)

(15)

第四步，計算第t年、年齡為x歲及以上的人年數之和(Tx,t)，公式為：

(16)

第五步，計算第t年、年齡為x歲的人的平均預期壽命(ex,t)，公式為：

(17)

2 實證分析——以江蘇省為例

2.1退休年齡“固化”對生命周期“三階段”發展現狀的影響 根據江蘇省近4次人口普查資料，運用式(1)可計算出江蘇省近4次人口普查的平均受教育年限情況，見表1。

表1 江蘇省近四次人口普查的平均受教育年限〔11〕

大專及以上的受教育年限取16年，高中和中專取12年，初中取9年，小學取6年，其他取1年

《義務教育法》規定年滿6周歲的兒童應接受義務教育，考慮到一些兒童可能推遲到7周歲，故這里將開始接受義務教育的平均年齡取為6.5歲。《中華人民共和國勞動法》規定最低工作年齡要達到16周歲。故初中及以下的人員接受完教育后一般還需等到16周歲才能進入工作崗位，且現實情況是他們完成教育之后并沒有直接工作，他們會花很長時間學習一技之長，然后走上工作崗位。于是實際的工作起始年齡會更遲一些。綜合考慮各種因素，通過實地調查可以得到江蘇省近4次人口普查的平均工作起始年齡，1982年17.85歲、1990年18.76歲、2000年19.56歲、2010年20.53歲。江蘇省在醫療衛生方面的大力投入使得江蘇省的人均預期壽命得到較大提高。表2給出了江蘇省近4次人口普查的平均預期壽命情況。江蘇省近4次人口普查生命周期三階段的時間長度及占整個生命周期的比例情況見表3。按照人力資源和社會保障部的相關資料，我國實際平均退休年齡為53歲左右。江蘇省平均退休年齡取為53歲。從時間長度來看，生命周期第一階段和第三階段都在不斷地提高，第二階段不斷降低。第一階段增加的時間長度等于第二階段減少的時間長度。第三階段時間長度的增加明顯大于第二階段的減少。從生命周期三個階段占整個生命周期的比例來看，第一階段和第三階段的占比在不斷提高，第二階段的占比在不斷下降。第一階段占比的增加幅度很小。第二階段的占比下降幅度非常明顯。

表2 江蘇省近4次人口普查的平均預期壽命

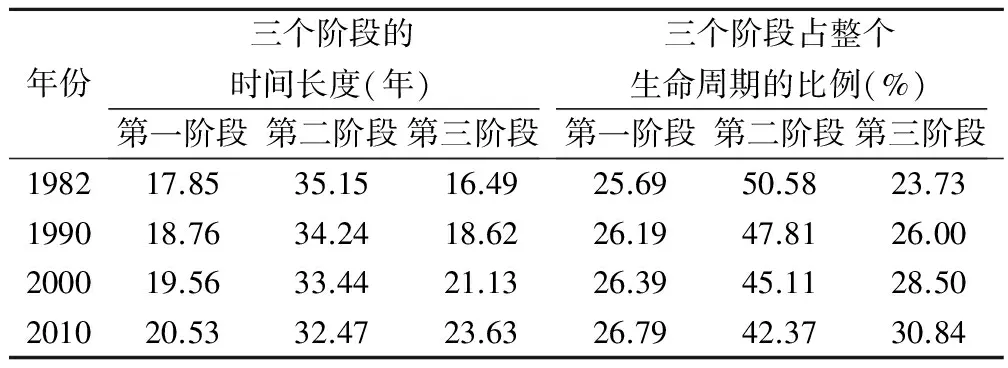
表3 江蘇省近4次人口普查生命周期三階段概況

2.2退休年齡“固化”對生命周期“三階段”發展趨勢的影響 江蘇省平均工作起始年齡在未來幾十年中穩步提高，幾乎每隔十年提高1歲左右。2020年21.45歲、2030年22.47歲、2040年23.50歲、2050年24.60歲。2050年，江蘇省的平均工作起始年齡已經將近25歲，和一個碩士生的工作起始年齡相當。根據江蘇省近四次人口普查時期的人口死亡率數據，運用有限數據下的Lee-Carter模型和生命表編制技術可以預測江蘇省未來幾十年的平均預期壽命情況，2020年78.76歲、2030年80.56歲、2040年81.69歲、2050年82.46歲。如果未來幾十年退休年齡政策依舊不變(平均退休年齡仍為53歲)，那么江蘇省未來幾十年生命周期三階段的時間長度及占整個生命周期的比例情況。見表4。

2.3退休年齡“固化”對法定工作年限及工作權利的影響 法定工作年限1982～2050年不斷下降，且下降幅度并不是太大，從1982年的35.15年下降至2050年28.40年，減少了7.75年(1990、2000、2010、2020、2030、2040年分別為34.24、33.44、32.47、31.55、30.53、29.50年)。但是法定工作年限占比卻下降得非常明顯，從1982年的50.58%下降至2050年的34.44%(1990、2000、2010、2020、2030、2040年分別為47.81%、45.11%、42.37%、40.06%、37.90%、36.11%)，減少了16.14%，遠遠大于法定工作年限的減少。這恰恰驗證了法定工作年限的占比在工作起始年齡及預期壽命提高的合力下減少得更為顯著。退休年齡“固化”對法定工作年限的不利影響體現在到了2040年，法定工作年限將不足30年，到了2050年，法定工作年限將首次小于退休階段的時間長度。這可能意味著工作期間創造的財富難以滿足退休時期的消費。

退休年齡固化對工作權利的影響是通過法定工作年限體現的。工作可以讓個體的生存得到基本保障。《勞動合同法》規定，勞動者開始依法享受基本養老保險待遇的，勞動合同終止。而國務院頒布的《勞動合同實施條例》(2008年)進一步規定，勞動者達到法定退休年齡的，勞動合同終止。因此勞動者只要達到法定退休年齡，勞動合同都將終止，無法得到勞動法的保護。可見，在我國，保障一個人的工作權利是以法定退休年齡為限的，只有在法定工作年限內的勞動者工作權才會受到法律的保護。然而退休年齡“固化”使得法定工作年限不斷縮短，這就意味著勞動者的工作權利被保護的期限被不斷壓縮。延遲退休年齡解決的核心問題之一就是保障人們擁有合理的法定工作年限，充分保障勞動者的工作權利。

3 討 論

延遲退休年齡具有客觀現實需要，同時在工作起始年齡及人均預期壽命不斷提高的情況下，延遲退休年齡符合人口自身發展的客觀規律。工作不但能讓人們得以生存，而且能讓人們熟練掌握某種技能，得到他人尊敬，獲取成就感，實現自我價值。因此，工作保障了個體的生存和發展。延遲退休年齡使得人們擁有合理的法定工作年限，保障人的生存權和發展權。

雖然延遲退休年齡改革具有客觀現實需要，但是目前卻面臨嚴重缺乏民眾支持的窘境〔7〕。首先，我國現行養老保險體系無論是從權利和機會，還是從規則方面均存在著公平性的不足〔12〕。其次，延遲退休年齡會給勞動力市場帶來沖擊，造成年輕人尤其是大學生的就業壓力〔4〕。因此退休年齡的改革需要認真研究破解上述障礙的策略，在此基礎上，研究漸進式延遲退休年齡的政策，并實施彈性退休制。這樣才能消除民眾的抵觸心理，有助于改革的順利推進。

本研究依然存在值得探討之處。首先，可以對其他預測方法的組合進行嘗試以便為工作起始年齡和人均預期壽命預測方法的優化提供參考。其次，退休年齡因性別而異，可以分別研究不同性別下退休年齡“固化”對生命周期“三階段”發展的影響，以便為延遲退休年齡差別化政策提供依據。最后，合理的法定工作年限究竟是多少尚不明確，如何利用國民轉移賬戶這一工具來測算合理的法定工作年限。

1鄧大松，劉昌平.中國養老社會保險基金敏感性實證研究〔J〕.經濟科學，2001；21(6)：13-20.

2鄭功成.對延遲退休年齡的基本認識〔N〕.光明日報，2012-9-12(14).

3袁 磊.延遲退休能解決養老保險資金缺口問題嗎？——72種假設下三種延遲方案的模擬〔J〕.人口與經濟，2014；15(4)：80-93.

4張車偉，仲大軍.中國是否應該推出彈性退休制度〔J〕.中國經濟周刊，2004；19(38)：20-3.

5蔡 昉.退休年齡：世界難題和中國國情〔J〕.今日中國論壇，2012；16(8)：21-2.

6唐 鈞.“延遲退休年齡”是否行得通〔J〕.人力資源，2010；23(11)：14-7.

7韓克慶.延遲退休年齡之爭——民粹主義與精英主義〔J〕.社會學研究，2013；45(2)：120-39.

8鄧聚龍.社會經濟灰色系統的理論與方法〔J〕.中國社會科學，1984；22(6)：47-60.

9Lee RD，Carter L.Modeling and forecasting the time series of U.S.mortality〔J〕.J Am Statist Assoc，1992；87(14)：659-75.

10王曉軍，任文東.有限數據下Lee-Carter模型在人口死亡率預測中的應用〔J〕.統計研究，2012；33(6)：87-94.

11江蘇省統計局.江蘇省統計年鑒〔M〕.北京：中國統計出版社，2012：1-25.

12黃健元，王 歡.退休及基本養老金領取條件研究〔R〕.南京：江蘇省社會保險學會，2014.