不完美維護下基于剩余壽命預測信息的設備維護決策模型

裴洪 胡昌華 司小勝 張正新 杜黨波

隨著現代高新科技的快速發展,航空航天和工業制造等領域的關鍵設備呈現出大規模和復雜化的趨勢,同時也對這類設備的可靠性和安全性提出了更苛刻的要求.為確保關鍵設備安全穩定運行,預測與健康管理(Prognostics and health management,PHM)作為一門新興技術受到了學術界和工業界的廣泛關注[1?2].視情維護(Condition-based maintenance,CBM)作為PHM的重要組成,能夠提高關鍵設備的安全性和可靠性,降低失效事件發生的概率.因而,CBM成為當前研究的熱點問題,涌現出了大量的學術成果[3?9].

根據修復程度不同,通常將維護分為完美維護、不完美維護和小修[10?11]三類.完美維護即設備的退化指標通過維護活動恢復至全新的狀態,適用于結構簡單的設備;小修即通過維護沒有改善設備的退化狀態,適用于結構復雜的設備[6].然而,在工程實際中,大部分維護活動均為不完美維護,即設備的退化指標通過維護活動無法恢復至全新的狀態,只能恢復至修復如新和修復如舊之間的某一狀態[6,10,12],例如為旋轉部件噴灑潤滑劑,對陀螺儀力矩器電流進行調整等.因此,相對于完美維護和小修,不完美維護更具一般性.不完美維護通常能夠減緩設備的退化過程,實現延壽的目的,受到了學者們的普遍關注[13?14].

現有文獻中,不完美維護的模型一般分為年齡減少模型、風險率增加模型及混合模型[15].Kijima等基于虛擬年齡的概念提出年齡減少模型以描述不完美維護活動對設備的影響[16].Nakagawa等從風險率的角度提出了風險率增加模型,通過引入調節因子刻畫風險率的變化趨勢,進而實現不完美維護模型的構建[17].Zhou等通過融合這兩類模型提出一種混合模型進一步改進了傳統的不完美維護模型,并在理論上驗證了該模型的合理性[18].上述不完美維護的模型分別從虛擬年齡和風險率的角度描述不完美維護影響,忽略了實際運行過程中獲取的性能退化數據,難以保證維護決策的準確性.隨著傳感技術的不斷發展,退化建模逐漸成為當前剩余壽命(Remaining life,RL)預測的主流方法[19].國內外有關從退化角度描述不完美維護模型的研究較為匱乏,亟需一種基于退化建模的不完美維護模型.Van等考慮了不完美維護對退化量的影響,認為不完美維護后退化量將減少一個隨機量[20].Wang等進一步研究這種影響,提出一種帶有負跳變的Wiener過程對維護活動干預下的設備RL進行預測,但沒有涉及維護決策的問題[14].Guo等針對任務導向型設備,基于Wiener退化過程構建出維護決策模型,通過引入殘余退化量的概念形象刻畫出不完美維護對退化量的影響,通過優化決策函數進而確定出最優預防性維護閾值[4].Zhang等通過引入隨機改善因子考慮了不完美維護對退化率的影響,從退化率的角度提出一種新的不完美維護模型,實現了陀螺儀的最優維護[6].以上基于退化建模的不完美維護模型,僅考慮不完美維護對退化量和退化率的單一影響,忽略了對兩者的雙重影響.一般而言,經歷不完美維護后,設備的退化量與退化率均會發生變化.因而為刻畫不完美維護的影響,在構建不完美維護模型時必須同時融入這兩方面的變化.

鑒于此,本文基于實際中普遍采用的定期檢測策略,提出一種考慮不完美維護活動影響的性能退化模型和維護決策模型,融合維護活動對設備退化量和退化率的雙重影響.1)基于Wiener過程分階段構建存在不完美維護干預的隨機退化模型,在首達時間的意義下推導出RL的解析概率分布;2)基于RL的預測結果,以檢測間隔和預防性維護閾值為決策變量建立維護決策模型,通過搜索方法求取檢測間隔和預防性維護閾值,從而最優實現工程設備的最優維護;3)數值仿真實驗驗證了本文模型的有效性,并對費用參數進行敏感性分析.

1 問題描述與模型假設

1.1 問題描述

對于關鍵工程設備而言,通過狀態監測技術能夠獲得設備當前的退化水平,將獲取的退化水平與預防性維護閾值進行比較從而指導維護活動,當其超出預防性維護閾值時進行預防性維護活動.在實際工程中,預防性維護一方面會改善設備的退化狀態,可用殘余退化量刻畫;另一方面將加快設備的退化速度.需要強調的是,本文提到的預防性維護均指不完美維護.為了保證設備的運行可靠性和經濟可承受性,工程實際中通常會限制預防性維護的次數N.當設備經歷N次預防性維護后,若其退化水平達到了預先設定的失效閾值w,意味著設備發生失效,為了避免財產損失和事故發生,在達到了失效閾值前需要對設備進行預防性替換,如圖1所示.

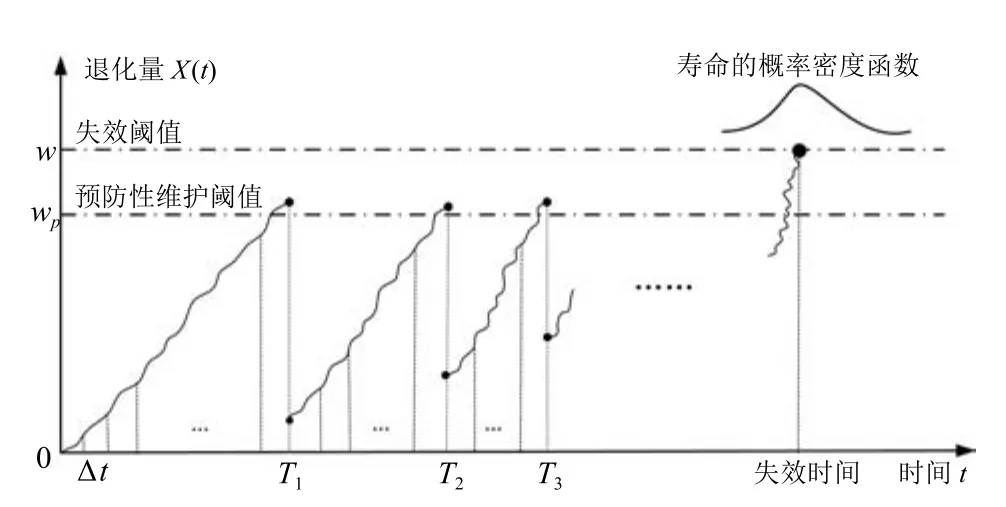
圖1 不完美維護干預下的設備退化軌跡Fig.1 Degradation trajectory under the in fluence of imperfect maintenance

針對上述維護活動干預下的設備退化過程,檢測間隔Δt與預防性維護閾值wp不僅影響設備的安全性和可靠性,同時對設備的運行成本也有一定影響.一方面,檢測間隔過大時,無法準確獲取設備退化水平的變化情況,貽誤了最佳維護和替換時機,難以保證設備的安全性和可靠性.另一方面,采取較小的檢測周期便于掌握設備退化狀態變化情況,但對于檢測成本較高的設備,頻繁的檢測將引起設備運行費用的提高,造成人力與物力的浪費.相似地,當預防性維護閾值過低時,設備的安全性和可靠性得到了有力保障,但頻繁的維護縮短了設備的運行時間,無法保證工程實際中的任務完成率;當預防性維護閾值過高時,設備運行過程中的安全性和可靠性難以得到保證.因此,合理的檢測間隔和預防性維護閾值能夠實現設備的最優維護,在維護決策領域發揮著舉足輕重的作用.

基于上述分析,本文主要研究以下內容:

1)如何基于Wiener過程分階段對考慮不完美維護活動影響的設備進行退化建模;

2)如何基于退化模型在首達時間意義下進行RL預測;

3)如何基于RL預測結果構建維護決策模型以及在維護決策模型基礎上確定最優檢測間隔和預防性維護閾值.

1.2 模型假設

1)設備經歷的檢測活動是定期的且完美的,能夠完全反映設備退化水平,單次檢測費用為Ci,檢測間隔為Δt,檢測所需時間可忽略不計;

2)設備經歷的預防性維護活動是不完美的,且對退化量與退化率有著雙重影響;

3)若檢測到設備的退化量超出失效閾值w時,設備需要進行失效性替換,相應費用為Cf,替換所需時間可忽略不計;

4)若檢測到設備的退化量介于預防性維護閾值wp與失效閾值w之間時,設備需要進行預防性維護,相應費用為Cp,維護所需時間可忽略不計;

5)若檢測到設備的退化量低于預防性維護閾值wp,設備繼續運行,不需要進行任何維護活動;

6)當設備經歷N次預防性維護后,若在設備發生失效前進行替換活動,即預防性替換,相應費用為Cr.

2 基于Wiener過程的退化建模和RL預測

基于Wiener過程的退化模型是一類常見的隨機退化模型,廣泛應用于設備腐蝕、機械磨損等實際退化過程中[4,6,14,21?22].本文采用Wiener過程對考慮維護活動影響的設備進行退化建模和RL分析,即基于Wiener過程分階段對退化過程進行建模,經過i次維護活動后進入壽命周期的第i+1階段,設備退化量可表示為[21?22]

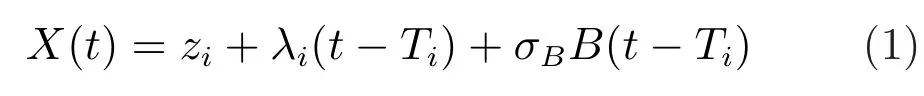
其中,X(t)為設備在t時刻的退化量,i(0≤i≤N)為t時刻前設備已經歷的維護次數,N為預防性維護的總數,zi為第i次維護后的殘余退化量,刻畫維護活動對退化量的影響,假設其概率密度函數滿足[4]

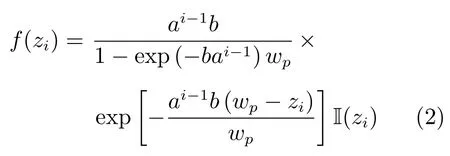
其中,a,b為超參數,I(zi)為示值函數,且有

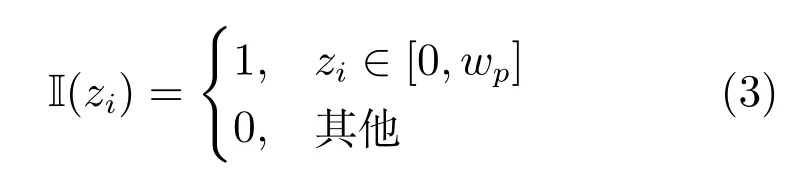
其中,wp為預防性維護閾值,一般由工業標準和專家經驗確定,且有z0=0.λi為第i次維護后漂移系數,刻畫維護活動對退化率的影響,且λi=(i+1)λ0,λ0為未進行維護時的漂移系數.值得注意的是,退化率的本質為退化量的一階導數.Ti為第i次維護時刻,σB為擴散系數,B(×)為標準布朗運動.

基于首達時間的概念,在第i次預防性維護后殘余退化量zi給定的情況下,設備的退化量首達預防性維護閾值wp的時間Ri,wp及首達失效閾值w的時間Ri,w可定義為

根據文獻[4,21],能夠進一步得到兩類首達時間Ri,wp和Ri,w的概率密度函數(Probability density function,PDF)和累積分布函數(Cumulative distribution function,CDF).

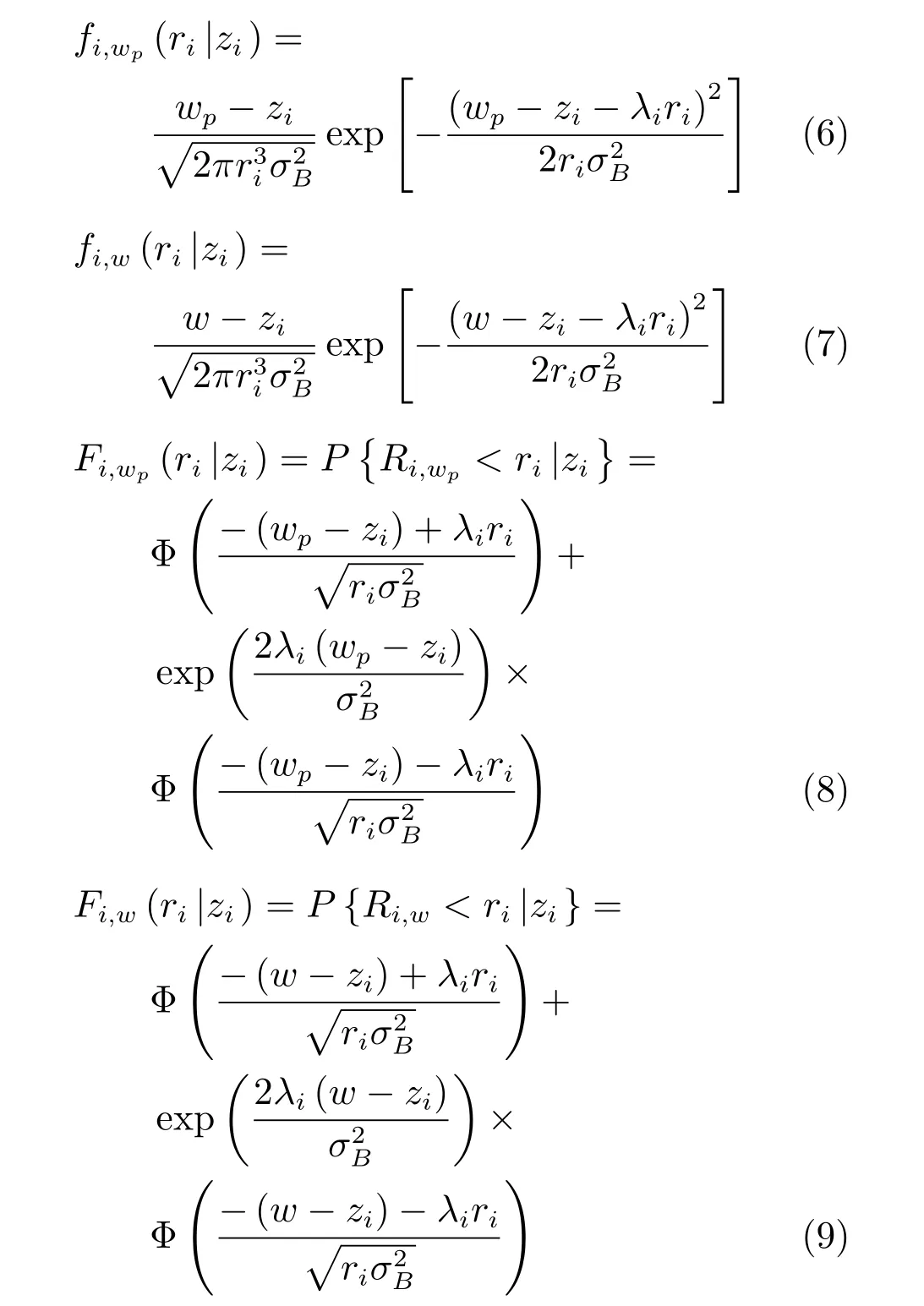
3 維護決策模型與求解

為了評估維護策略的性能,本文選擇長期期望維護費用率函數作為主要指標對維護策略進行性能分析.具體地,以檢測間隔與預防性維護閾值為決策變量,最小化長期期望維護費用率函數為準則,根據更新報酬理論,維護決策模型表示為[3]

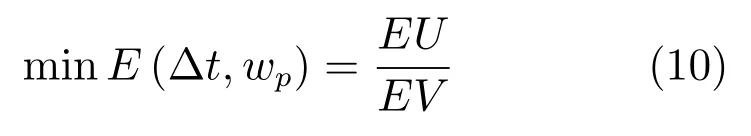
其中,EU為設備壽命周期內的運行總費用,包含預防性維護費用、檢測費用、預防性替換費用和失效性替換費用,EV為設備壽命周期的期望.

基于上述分析,EU可進一步表示為

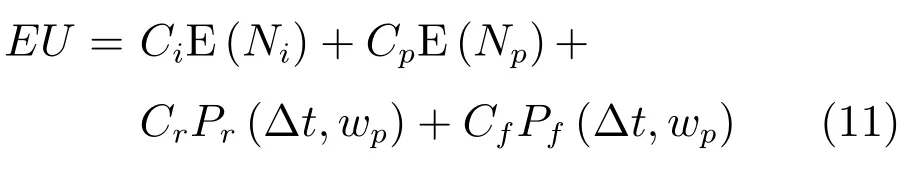
其中,Ci為檢測費用,Cp為預防性維護費用,Cr為預防性替換費用,Cf為失效性替換費用,且Ci＜Cp＜Cr＜Cf.E(Ni)為檢測次數的期望值,E(Np)為預防性維護次數的期望值,Pr(Δt,wp)為設備進行預防性替換的概率,Pf(Δt,wp)為設備進行失效性替換的概率.

設備壽命周期的終結通常分為兩種情形:1)預防性替換引起壽命周期的計劃終止;2)失效性替換引起設備壽命周期的意外終止.

3.1 預防性替換

設備進行預防性替換的過程如圖2所示.

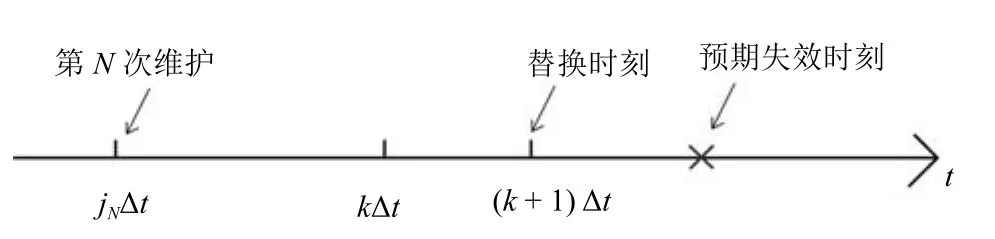
圖2 預防性替換過程Fig.2 Process of the preventive replacement

從圖2可以看出,設備進行預防性替換需要滿足兩個前提條件:1)設備進行了N次預防性維護;2)失效前對設備進行更換.假定預防性替換時刻為(k+1)Δt(k≥N),預防性替換活動通過對設備進行更換進而保證設備運行的安全性和可靠性,且第i(1≤i≤N)次預防性維護時刻為jiΔt.由于預防性維護時刻jiΔt具有隨機性,因而為確定此時刻進行預防性維護的概率P(ji),給出如下定理.

定理1.對于不完美維護活動干預的隨機退化設備,在jiΔt(i∈[1,N],i∈N+)時刻進行預防性維護的概率P(ji)能夠表示為

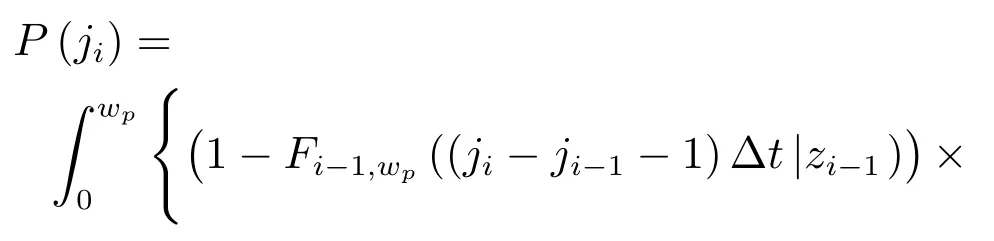
證明.在jiΔt時刻進行預防性維護,即(ji?1)Δt的退化量X((ji?1)Δt)低于預防性維護閾值wp,且jiΔt的退化量X(jiΔt)介于預防性維護閾值wp和失效閾值w之間,因而,jiΔt時刻進行預防性維護的概率P(ji)可進一步表示為

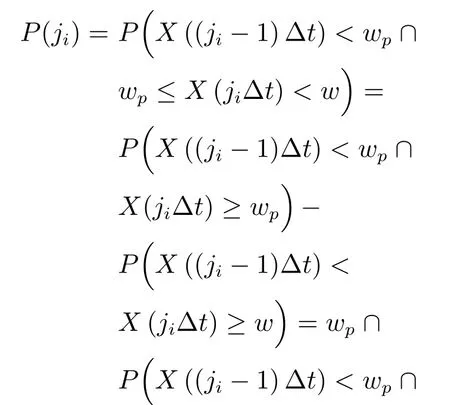
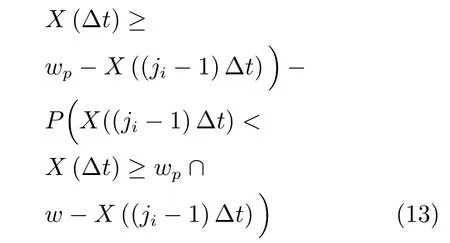
值得注意的是,式(13)的推導利用了Wiener過程的獨立增量特性,即X(jiΔt)?X((ji?1)Δt)=X(Δt).在不考慮殘余退化量zi?1隨機性的情況下,同時基于獨立事件的相關知識,則jiΔt時刻進行預防性維護的條件概率P(ji|zi?1)可表示為

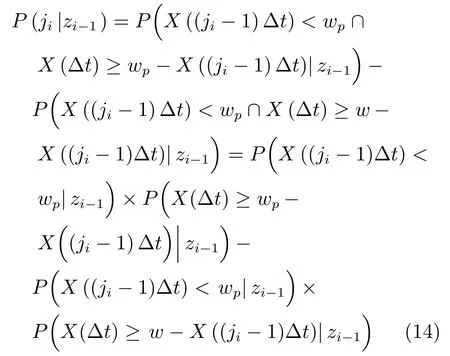
考慮(ji?1)Δt時刻退化量X((ji?1)Δt)的隨機性,式(14)中的幾項概率為

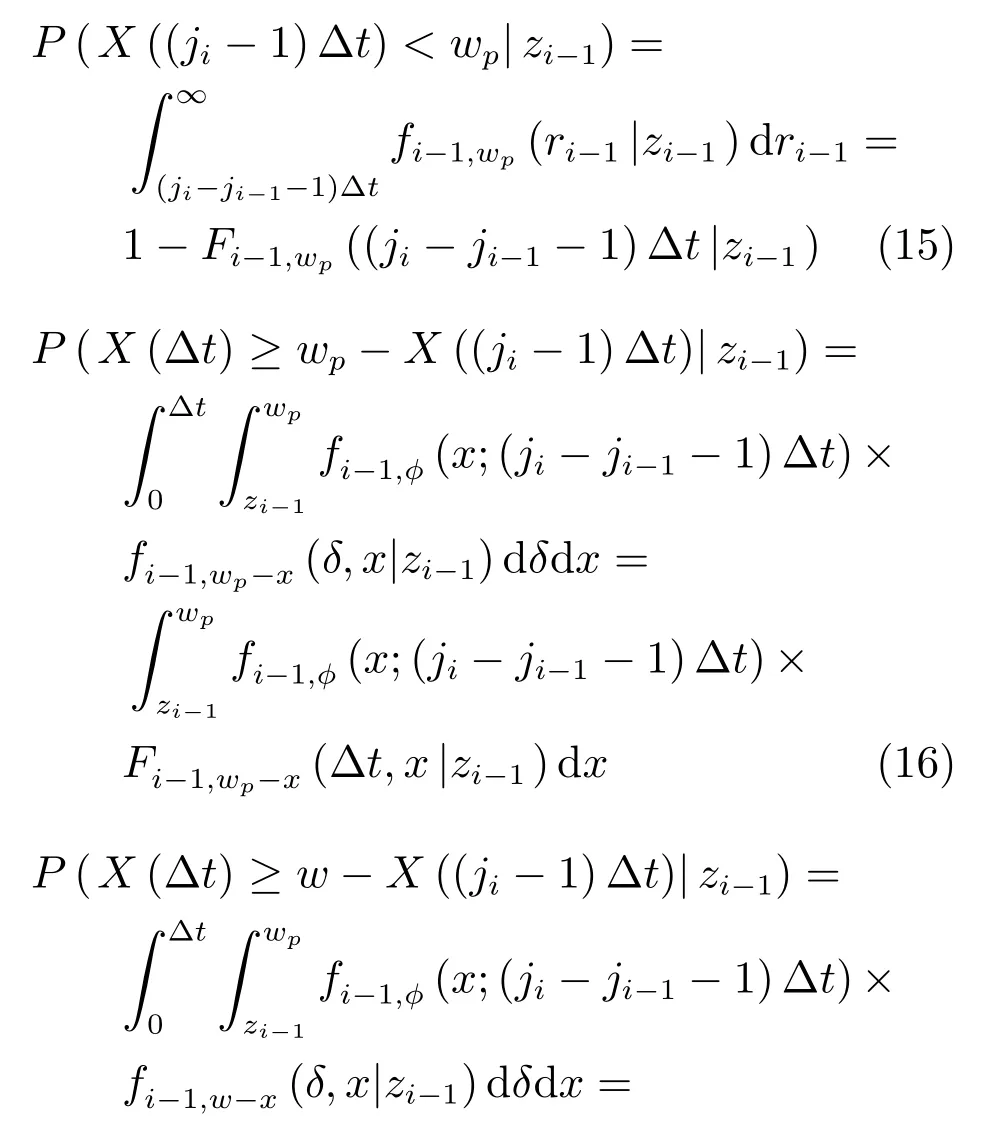
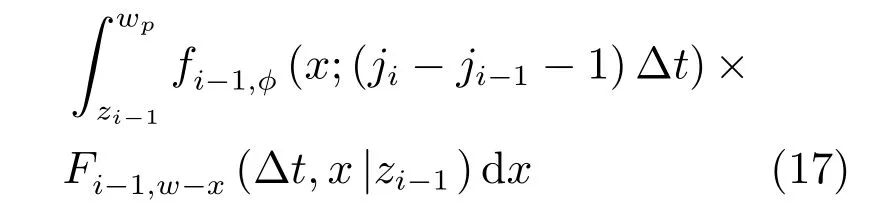
將式(15)～(17)分別代入式(14),可得jiΔt時刻進行預防性維護的條件概率P(ji|zi?1).

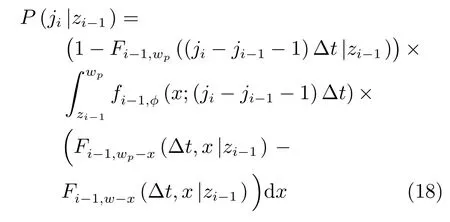
根據全概率公式,jiΔt時刻進行預防性維護的概率P(ji)可表示為

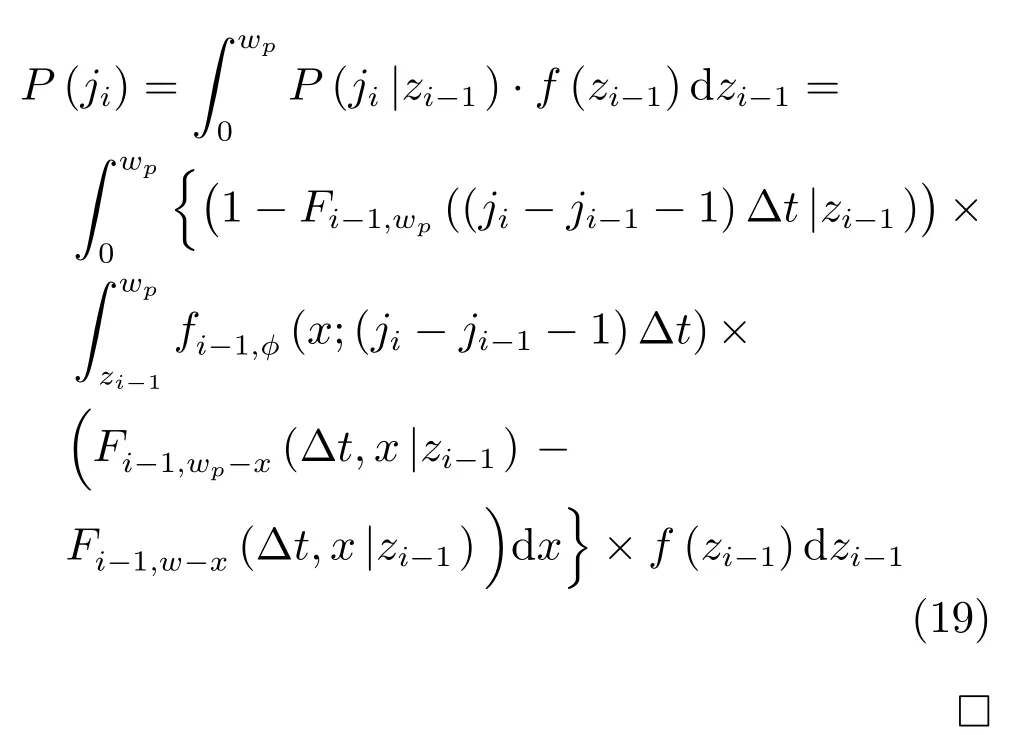
基于上述描述,設備在(k+1)Δt(k≥N)進行預防性替換之前,經歷了N次預防性維護,這些維護不僅自身相互獨立而且與維護后的替換活動相互獨立.假定設備在kΔt時刻的退化量為X(kΔt),在(k+1)Δt時刻的退化量為((k+1)Δt),根據上述定理的結論,設備在(k+1)Δt(k≥N)進行預防性替換概率Pr(k+1,N)可表示為

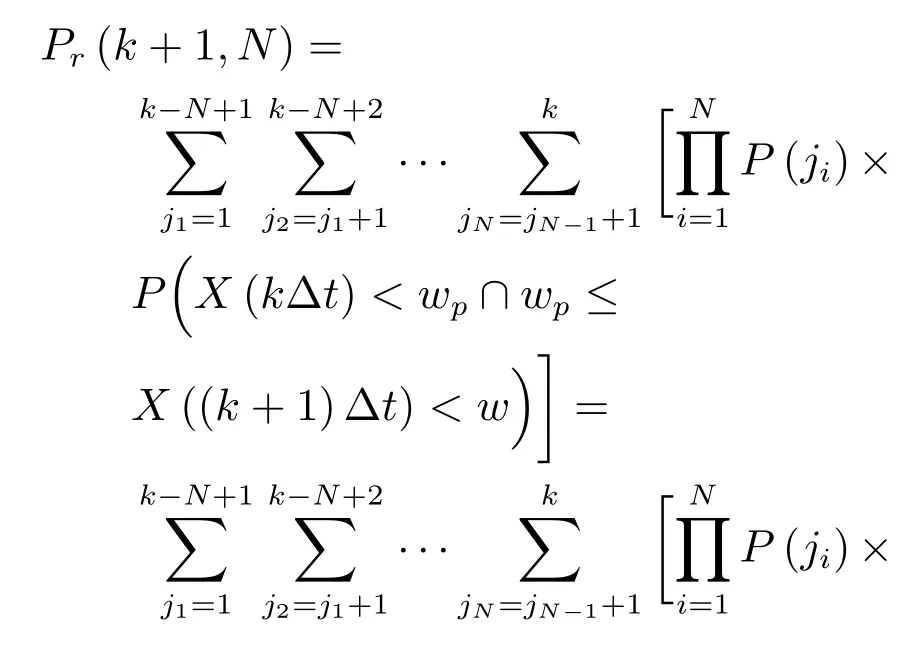
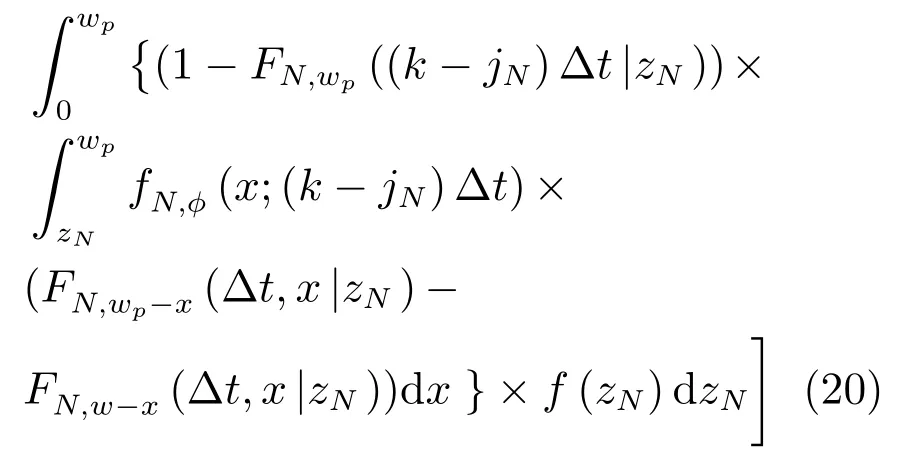
設備在N次預防性維護后進行預防性替換的概率Pr(Δt,wp)為

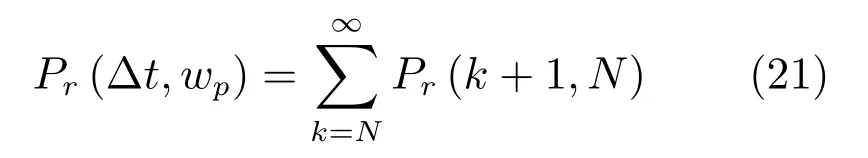
3.2 失效性替換

根據概率論中對立事件的關系,設備進行失效性替換的概率可表示為

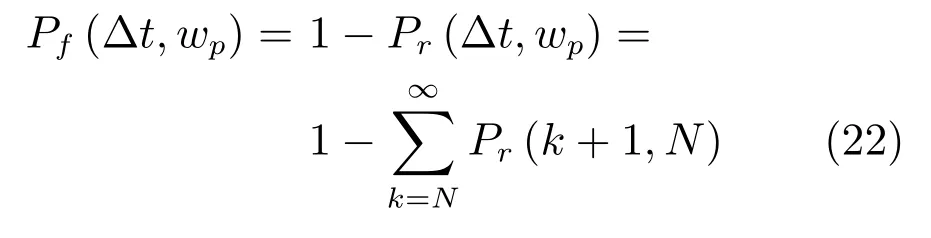
具體地,由于設備性能退化的隨機性,設備在壽命周期內的任何階段內均有可能發生失效,失效后進行的替換活動均為失效性替換.假定設備在(kΔt,(k+1)Δt]發生失效,根據失效前經歷維護活動的次數,將失效性替換分為兩種情況.

1)設備失效前未進行預防性維護活動.如圖3(a)所示,設備在壽命周期的第一階段內,即第一次預期維護前突發失效,通過狀態檢測技術失效狀態會在下一個檢測時刻(k+1)Δt發現,進而對設備進行更換,實現壽命周期的交替循環.

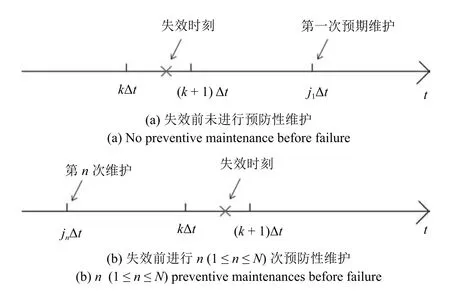
圖3 預防性替換過程Fig.3 Process of the preventive maintenance

設備失效前未進行預防性維護活動意味著預防性維護活動無法在延壽方面發揮作用,等價于在設備壽命周期的第一階段內在kΔt時刻的退化量X(kΔt)小于預防性維護閾值wp,在(k+1)Δt時刻的退化量X((k+1)Δt)大于失效閾值w,則設備在失效前未進行預防性維護活動的概率Pf(k+1,0)可表示為

2)設備失效前進行了n(1≤n≤N)次預防性維護.如圖3(b)所示,設備經歷n次預防性維護后進入在壽命周期第n+1階段,此時設備在(kΔt,(k+1)Δt]區間突發失效,由于預防性維護次數n＞0,意味著預防性維護活動在延壽方面發揮了作用.基于定理1,則設備在失效前進行n(1≤n≤N)次預防性維護的概率為

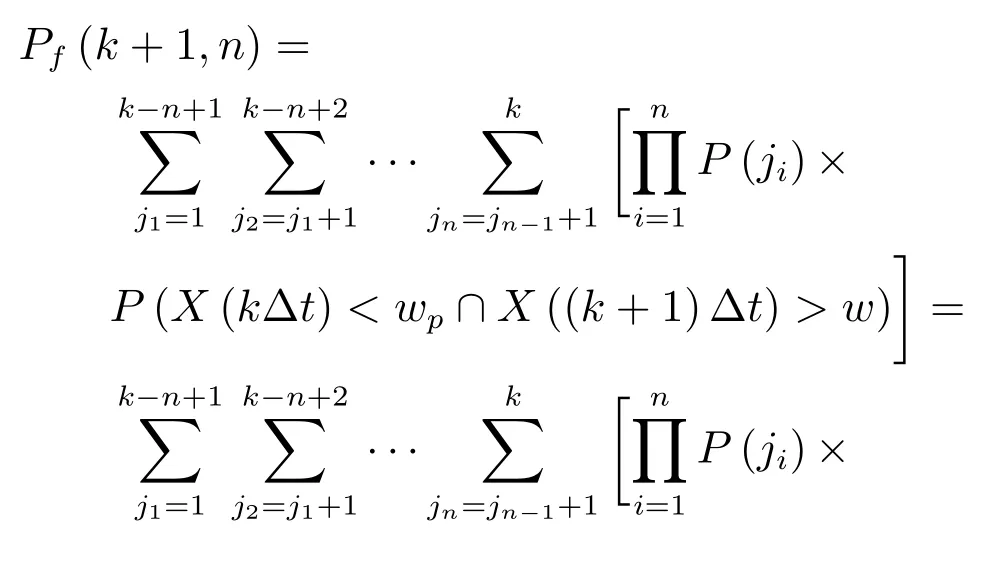
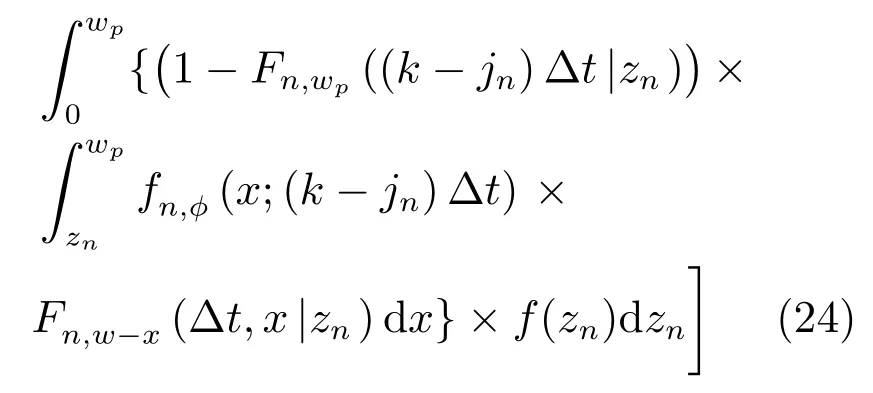
通過以上分析,能夠得到維護決策模型的相關參數,其他參數(EV,E(Ni),E(Np))可基于上述參數推導得到

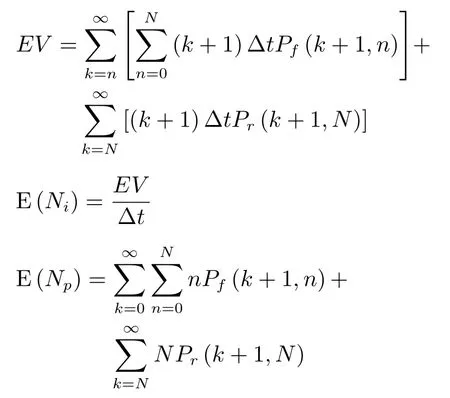
EV表示設備壽命周期的期望,由于預防性替換與失效性替換的替換時刻均為(k+1)Δt(k≥N),根據概率統計知識可得壽命周期的期望值;E(Ni)表示檢測次數的期望值,由于檢測間隔為Δt,根據設備壽命周期的期望與檢測間隔的比值即可得出檢測次數的期望值;E(Np)表示預防性維護次數的期望值,與壽命周期的期望計算過程相似,同樣可根據概率統計相關知識得到預防性維護次數的期望值.

將上述參數代入式(10)定義的維護決策模型中,利用MATLAB軟件通過搜索的方法尋求最優的檢測間隔和預防性維護閾值,并進行敏感度分析,研究費用參數對最小長期期望維護費用率的影響.

4 仿真實驗

本節通過仿真實驗對本文模型的有效性和優越性進行驗證,確定最優的檢測間隔和預防性維護閾值,實現工程實際中的最優維護,同時對相關費用參數的敏感性進行系統分析.在實驗中,將本文模型記為模型1,將文獻[4]模型記為模型2,通過對比兩種模型得出最優長期期望維護費用率,實現兩種模型的比較.

4.1 參數設置

假定設備的退化過程服從式(1)定義的Wiener過程,其中,未進行維護時的漂移系數λ0和擴散系數σB分別設為0.3和0.2,殘余退化量的參數(a,b)設為0.2和0.001.以周期Δt對設備的退化量進行定期檢測,單位為小時,當檢測到設備當前退化量超出失效閾值w=10時,意味著設備發生失效而停機,此時必須進行失效性替換;當檢測到退化量介于失效閾值w與預防性維護閾值wp之間時,應立即采取預防性維護以保證設備運行可靠性,經過N=3次預防性維護后,當退化量再次超出預防性維護閾值wp且未發生故障時,立即進行預防性替換.基于式(10),為得到長期期望維護費用率,需要給定檢測、預防性維護與預防性替換等相關費用,相關費用參數可參考表1.

表1 相關費用參數Table 1 Cost parameters

4.2 結果分析與討論

參數設置完成后,基于模型1中的各參數,能夠得出設備進行預防性替換的概率Pr(Δt,wp),設備進行失效性替換的概率Pf(Δt,wp),監測次數的期望值E(Ni),預防性維護次數的期望值E(Np)和設備壽命周期的期望EV,將所得結果代入式(10),得到長期期望維護費用率E(Δt,wp).為研究費用率函數與兩類決策變量間的關系,利用多維搜索的方法描繪出模型1費用率的函數圖像,如圖4所示.從圖4可以看出,當Δt=0.5小時且wp=9時,長期期望維護費用率達到最小,最小值為13.02元/小時,即實現工程實際中的最優維護.

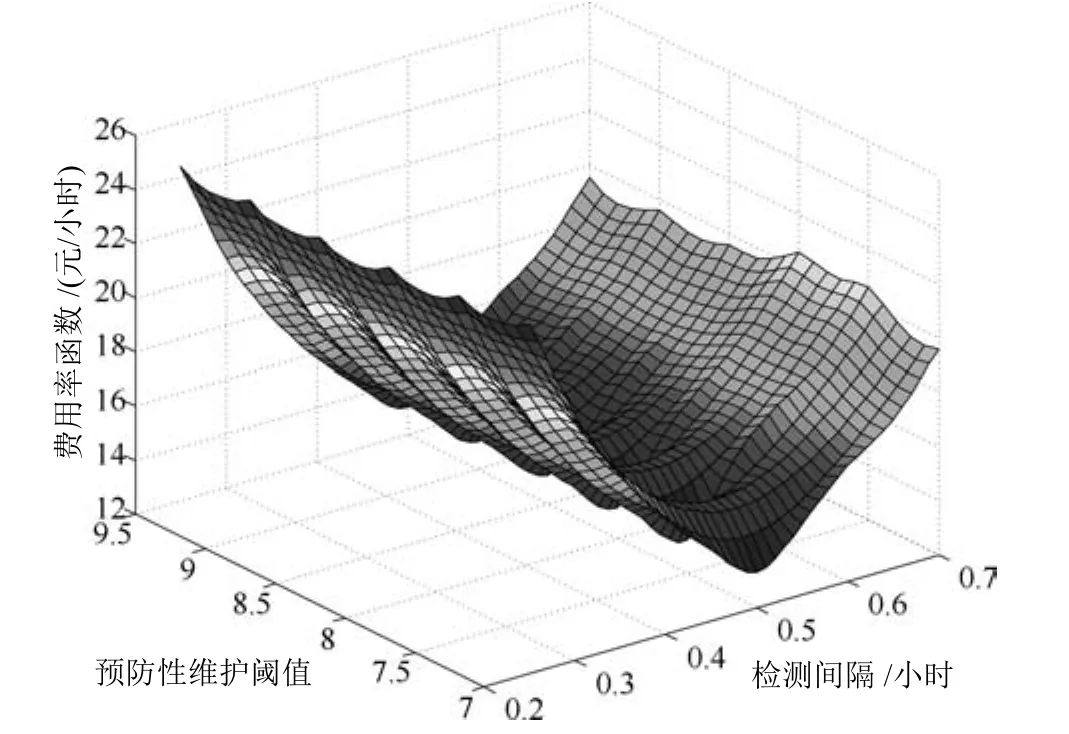
圖4 模型1的決策變量與長期期望維護費用率的關系Fig.4 Relationship between the decision variables of model 1 and long term expected maintenance cost rate

對于模型2,為研究預防性維護閾值與長期期望維護費用率的關系,需要固定檢測間隔Δt,這里設定檢測間隔Δt=0.45小時.由于模型2僅有一個決策變量,能夠較為方便地通過搜索方法確定最優預防性維護閾值.預防性維護閾值與長期期望維護費用率的關系如圖5所示.從圖5可以看出,當wp＜9時,長期期望維護費用率隨著預防性閾值的增加單調遞減;當wp＞9時,長期期望維護費用率隨著預防性閾值的增加單調遞增;當wp=9時,長期期望維護費用率最小,最小值為14.31元/小時.

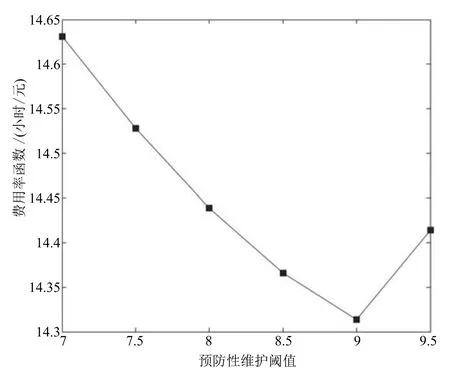
圖5 模型2的決策變量與長期期望維護費用率的關系Fig.5 Relationship between the decision variables of model 2 and long term expected maintenance cost rate

通過對比圖4與圖5能夠發現,模型1得出的最優長期期望維護費用率明顯小于模型2得出的最優長期期望維護費用率,主要原因是模型1優化了維護決策模型中的兩個決策變量,而模型2僅優化了維護決策模型中的一個決策變量.驗證了本文模型的有效性與優越性.

下面重點研究本文模型的最優維護策略對維護費用參數的敏感性.

為分析最優維護策略對維護費用參數的敏感性,本文基于固定變量法研究某種費用參數與長期期望維護費用率的關系.首先研究檢測費用Ci對最優維護策略與最優長期期望維護費用率的影響.為方便研究,本文假定檢測費用Ci滿足1元≤Ci≤50元,其他費用參數固定不變,對于不同的檢測費用,通過上述維護決策模型,能夠得到不同的最優維護策略及最優長期期望維護費用率,如圖6所示.

從圖6能夠看出,對于最優長期期望維護費用率而言,當檢測費用Ci從1元變化至50元,最優長期期望維護費用率從12元/小時線性變化至24.4元/小時,意味著檢測費用Ci每增加1元,最優長期期望維護費用率增加約0.25元/小時,由于最優長期期望維護費用率在整個區間內始終保持這種線性變化關系,因而最優長期期望維護費用率受到檢測費用的影響最為明顯.對于檢測間隔而言,隨著檢測費用的變化,檢測間隔分別在Ci=6,12,34,45元附近有明顯的上升,每次上升約0.05小時,檢測間隔在檢測費用的大部分區間內均保持恒定,因而檢測間隔受到檢測費用的影響較為明顯.檢測間隔上升的主要原因是當檢測費用較低時,頻繁的檢測能夠及時掌握設備的退化狀態,保證設備的運行可靠性,降低設備的失效風險,因而此時最優檢測間隔較短;隨著檢測費用的增長,頻繁的檢測將導致檢測成本的上升,因而檢測間隔隨之提高.對于預防性維護閾值而言,隨著檢測費用的變化,預防性維護閾值僅在Ci=17,34元附近有明顯的下降,第一次下降約0.2元,第二次下降約0.1元,預防性維護閾值在檢測費用的大部分區間內均保持恒定,因而預防性維護閾值受到檢測費用的影響相對最小,即預防性維護閾值對檢測費用的敏感性最差,總體上會略微下降,以降低設備失效的概率.

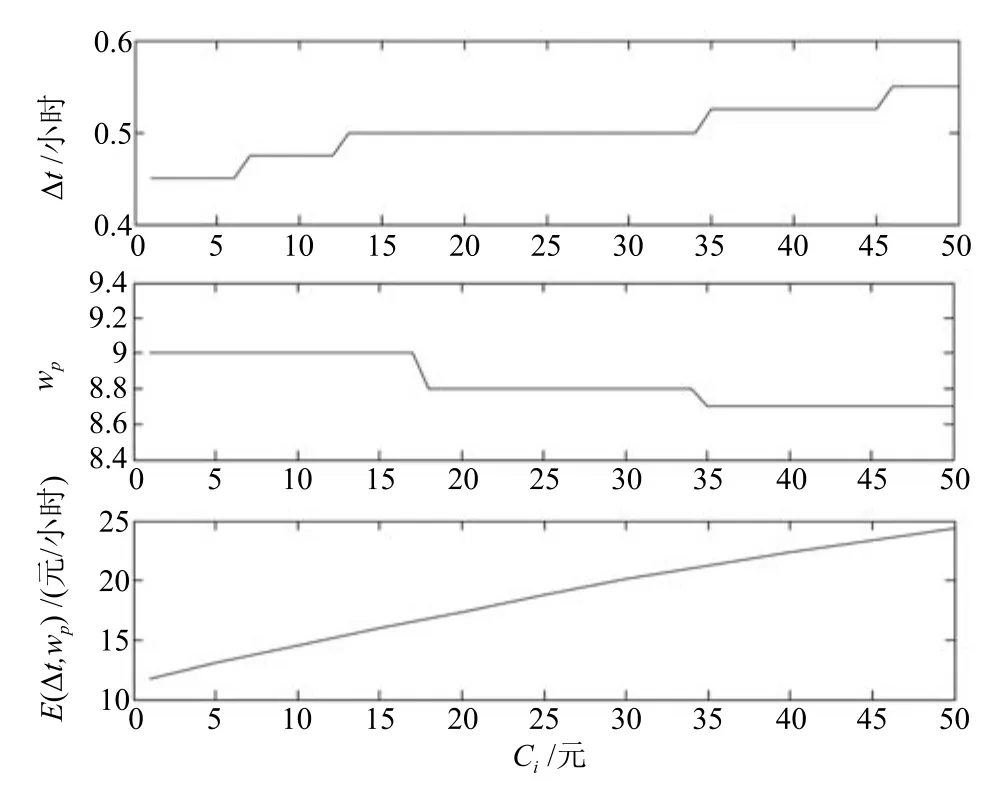
圖6 檢測費用與最優維護策略及最優長期期望維護費用率的關系Fig.6 Relationship between preventive maintenance cost and maintenance policy with the optimal long term expected maintenance cost rate

圖7給出了預防性維護費用與最優維護策略及最優長期期望維護費用率的關系,假定預防性維護費用Cp滿足5元≤Cp≤180元,其他參數固定不變.從圖7可以看出,對于最優長期期望維護費用率而言,當預防性維護費用Cp從5元變化至130元,最優長期期望維護費用率從8.93元/小時線性變化至17.51元/小時,意味著預防性維護費用Cp每增加1元,最優長期期望維護費用率增加約0.069元/小時；當Cp≥130元時,最優長期期望維護費用率基本保持恒定,與文獻[23]中的結果相一致.由于最優長期期望維護費用率在預防性維護費用的大部分區間內均保持上述線性變化關系,因而最優長期期望維護費用率受到預防性維護費用的影響最為明顯.對于預防性維護閾值而言,隨著預防性維護費用的變化,預防性維護閾值分別在Cp=20,53,84,129元附近有明顯的上升,每次上升約0.2元,預防性維護閾值在預防性維護費用的大部分區間內均保持恒定,因而預防性維護閾值受到預防性維護費用的影響較為明顯.預防性維護閾值上升的主要原因是當預防性維護費用較低時,較低的預防性維護閾值可提高維護的頻率,保證了設備運行的安全性與可靠性；隨著預防性維護費用的增長,頻繁的維護將導致維護成本的上升,因而預防性維護閾值隨之提高.對于檢測間隔而言,隨著預防性維護費用的變化,檢測間隔僅在Cp=20元附近上升至0.5小時,之后一直保持在0.5小時不變,因而檢測間隔受到預防性維護費用的影響相對最小,即檢測間隔對預防性維護費用的敏感性最差.

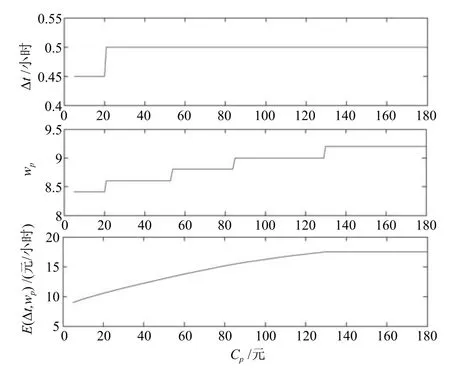
圖7 預防性維護費用與最優維護策略及最優長期期望維護費用率的關系Fig.7 Relationship between monitoring cost and maintenance policy with the optimal long term expected maintenance cost rate

圖8表示預防性替換費用與最優維護策略及最優長期期望維護費用率的關系,假定預防性替換費用Cr滿足50元≤Cr≤500元,其他參數固定不變.從圖8可以看出,對于最優長期期望維護費用率而言,當預防性替換費用Cr從50元變化至500元,最優長期期望維護費用率從8.4元/小時線性變化至21.1元/小時,意味著預防性替換費用Cr每增加1元,最優長期期望維護費用率增加約0.028元/小時,由于最優長期期望維護費用率在整個區間內始終保持這種線性變化關系,因而最優長期期望維護費用率受到預防性替換費用的影響最為明顯.對于預防性維護閾值而言,隨著預防性替換費用的變化,預防性維護閾值分別在Cr=90,160,235,355,460元附近呈現明顯的降低趨勢,每次降低約0.2元,預防性維護閾值在預防性替換費用的大部分區間內均保持恒定,因而預防性維護閾值受到預防性替換費用的影響較為明顯.對于檢測間隔而言,當預防性替換費用50元≤Cr≤450元 時,檢測間隔始終保持在0.5小時附近,預防性替換費用Cr在450元附近時,檢測間隔會上升至0.55小時.檢測間隔上升的原因是當預防性替換費用在失效性替換費用附近時,預防性替換已難以降低設備的維護成本,意味著無需再進行提前更換,因而檢測間隔會有所上升.

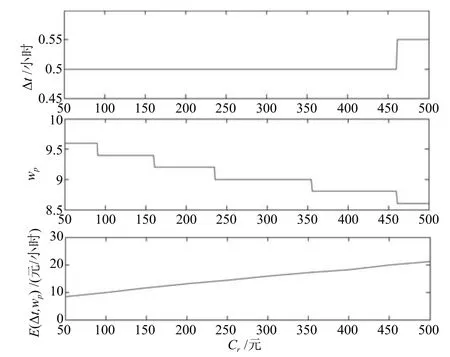
圖8 預防性替換費用與最優維護策略及最優長期期望維護費用率的關系Fig.8 Relationship between preventive replacement cost and maintenance policy with the optimal long term expected maintenance cost rate

綜合上述實驗研究可以看出,1)在給定的費用參數條件下,本文模型能夠對工程設備的檢測間隔Δt與預防性維護閾值wp進行聯合優化,保證了設備運行的安全性和可靠性,延長了設備的服役期限,降低了設備的維護成本,進而實現了設備的最優維護.2)對于不同的費用參數,最優維護策略的敏感程度具有明顯的差異性.具體地,對于檢測費用而言,檢測間隔的敏感程度高于預防性維護閾值的敏感程度;相反,對于預防性維護費用和預防性替換費用而言,預防性維護閾值的敏感程度遠高于檢測間隔的敏感程度.長期期望維護費用率對于不同費用參數的敏感程度具有一定相似性.一般來說,隨著費用參數的增長,長期期望維護費用率將線性遞增.

5 結論

本文針對工程關鍵設備,基于實際中普遍采用的定期檢測策略,提出一種考慮不完美維護活動影響的性能退化模型和維護決策模型,融合了不完美維護對設備退化量和退化率的雙重影響,確定了最優的檢測間隔和預防性維護閾值,進而達到了降低設備維護費用的最終目的.由于Wiener過程通常僅用來描述線性退化過程,無法準確刻畫出非線性退化過程,因而采用本文模型對非線性退化設備進行維護決策時,維護決策的結果會受到嚴重影響,難以實現工程實際中的最優維護.針對該模型的不足,下一步將研究如何基于非線性擴散過程對不完美維護干預下的非線性退化設備進行剩余壽命預測,以及如何利用剩余壽命預測信息進行維護決策模型的構建.

References

1 Pecht M G.Prognostics and Health Management of Electronics.New Jersey,USA:John Wiley,2008.

2 Zhou Dong-Hua,Wei Mu-Heng,Si Xiao-Sheng.A survey on anomaly detection,life prediction and maintenance decision for industrial processes.Acta Automatica Sinica,2013,39(6):711?722(周東華,魏慕恒,司小勝.工業過程異常檢測、壽命預測與維修決策的研究進展.自動化學報,2013,39(6):711?722)

3 Cheng Zhi-Jun,Guo-Bo.Optimization of inspection and maintenance policy for deteriorating system with semi-Markov decision process.Acta Automatica Sinica,2007,33(10):1101?1104(程志君,郭波.基于半Markov決策過程的劣化系統檢測與維修優化模型.自動化學報,2007,33(10):1101?1104)

4 Guo C M,Wang W B,Guo B,Si X S.A maintenance optimization model for mission-oriented systems based on Wiener degradation.Reliability Engineering and System Safety,2013,111:183?194

5 Tu Hui-Ling,Zhang Sheng-Gui,Si Shu-Bin,Dui Hong-Yan.The integrated importance measure of multi-state compound systems for maintenance processes.Acta Automatica Sinica,2014,40(1):126?134(涂慧玲,張勝貴,司書賓,兌紅炎.面向維修過程的多態混聯系統綜合重要度計算方法.自動化學報,2014,40(1):126?134)

6 Zhang M M,Gaudoin O,Xie M.Degradation-based maintenance decision using stochastic filtering for systems under imperfect maintenance.European Journal of Operational Research,2015,245(2):531?541

7 Zhang M M,Ye Z S,Xie M.A condition-based maintenance strategy for heterogeneous populations.Computers and Industrial Engineering,2014,77:103?114

8 Xu Xiao-Bin,Zhang Zhen,Li Shi-Bao,Wen Cheng-Lin.Fault diagnosis based on fusion and updating of diagnosis evidence.Acta Automatica Sinica,2016,42(1):107?121(徐曉濱,張鎮,李世寶,文成林.基于診斷證據靜態融合與動態更新的故障診斷方法.自動化學報,2016,42(1):107?121)

9 Gao Wen-Ke,Zhang Zhi-Sheng,Zhou Yi-Fan,Liu Yang,Liu Qi.Reliability modeling and maintenance policy for main and supplementary parallel system with failure interaction and imperfect detection.Acta Automatica Sinica,2015,41(12):2100?2114(高文科,張志勝,周一帆,劉飏,劉祺.存在故障相關及不完備檢測的主輔并聯系統可靠性建模與維修策略.自動化學報,2015,41(12):2100?2114)

10 Pham H,Wang H Z.Imperfect maintenance.European Journal of Operational Research,1996,94(3):425?438

11 Mercier S,Castro I T.On the modelling of imperfect repairs for a continuously monitored gamma wear process through age reduction.Journal of Applied Probability,2013,50(4):1057?1076

12 Van P D,Voisin A,Levrat E,Lung B.Remaining useful life based maintenance decision making for deteriorating systems with both perfect and imperfect maintenance actions.In:Proceedings of the 2013 IEEE Conference on Prognostics and Health Management.Gaithersburg,MD,USA:IEEE,2013.1?9

13 Castro I T.A model of imperfect preventive maintenance with dependent failure modes.European Journal of Operational Research,2009,196(1):217?224

14 Wang Z Q,Hu C H,Wang W B,Si X S.A simulationbased remaining useful life prediction method considering the in fluence of maintenance activities.In:Proceedings of the 2014 Prognostics and System Health Management Conference.Zhangjiajie,China:IEEE,2014.284?289

15 Khatab A.Hybrid hazard rate model for imperfect preventive maintenance of systems subject to random deterioration.Journal of Intelligent Manufacturing,2015,26(3):601?608

16 Kijima M.Some results for repairable systems with general repair.Journal of Applied Probability,1989,26(1):89?102

17 Nakagawa T.Sequential imperfect preventive maintenance policies.IEEE Transactions on Reliability,1988,37(3):295?298

18 Zhou X J,Xi L F,Lee J.Reliability-centered predictive maintenance scheduling for a continuously monitored system subject to degradation.Reliability Engineering and System Safety,2007,92(4):530?534

19 Si X S,Wang W B,Hu C H,Zhou D H.Remaining useful life estimation—a review on the statistical data driven approaches.European Journal of Operational Research,2011,213(1):1?14

20 Van P D,Bérenguer C.Condition-based maintenance with imperfect preventive repairs for a deteriorating production system.Quality and Reliability Engineering International,2012,28(6):624?633

21 Si Xiao-Sheng,Hu Chang-Hua,Zhou Dong-Hua.Nonlinear degradation process modeling and remaining useful life estimation subject to measurement error.Acta Automatica Sinica,2013,39(5):530?541(司小勝,胡昌華,周東華.帶測量誤差的非線性退化過程建模與剩余壽命估計.自動化學報,2013,39(5):530?541)

22 Huang Z Y,Xu Z G,Ke X J,Wang W H,Sun Y X.Remaining useful life prediction for an adaptive skew-Wiener process model.Mechanical Systems and Signal Processing,2017,87:294?306

23 Ge En-Shun,Li Qing-Min,Zhang Guang-Yu,Yang Mei-Ling.Optimization of condition-based maintenance for degradation systems under imperfect maintenance.Acta Aeronautica et Astronautica Sinica,2013,34(2):316?324(葛恩順,李慶民,張光宇,楊美玲.考慮不完全維修的劣化系統最優視情維修策略.航空學報,2013,34(2):316?324)