基于G-AHM模型的群體水平評估認知診斷模型研究
王郁
摘 ?要: 為了解決群體認知診斷評估中以個體為診斷對象所導致的判據不直觀且單一,難以針對性進行補救教學,以及評估誤差大,評估過程所需的時間、物力及人力成本較高等問題。基于G?AHM模型,研究并開發了一種群體水平評估的認知診斷模型。該模型使用貝葉斯和相似度判別法,并結合GIRT、認知診斷模型的特點,具有診斷成本低、誤差小等優點。經Monte Carlo模擬仿真和實證測試后發現,該認知診斷模型對群體水平認知診斷的效果良好,能夠為相關高校群體心理健康水平評估認知診斷模型的研究與開發提供支持。
關鍵詞: G?AHM; 群體水平評估; 認知診斷; 心理健康; Monte Carlo模擬; 貝葉斯
中圖分類號: TN911?34; TP393 ? ? ? ? ? ? ? ? 文獻標識碼: A ? ? ? ? ? ? ? ? ? ?文章編號: 1004?373X(2018)10?0105?03
Abstract: ?A cognitive diagnosis model for group level evaluation is studied and developed based on G?AHM model to solve the problems such as unintuitive and single judgment basis, difficulty to conduct remedial teaching objectively, big evaluation error, and high cost of time, material and labor of the evaluation process in group cognitive diagnosis evaluation which takes the individual as the diagnosis object. The model has the advantages such as low diagnosis cost and small error by adopting the Bayesian and similarity decision methods and combining the characteristics of GIRT and cognitive diagnosis model. The results of Monte Carlo simulation and empirical tests show that this cognitive diagnosis model has a good effect on group?level cognitive diagnosis and can provide support for relative research and development of the cognition diagnosis model for college students′ mental health level evaluation.
Keywords: G?AHM; group?level evaluation; cognitive diagnosis; mental health; Monte Carlo simulation; Bayesian
0 ?引 ?言
認知診斷評估旨在研究人類心理活動的加工機制和活動規律,進而對群體(個體)的認知現狀進行診斷。經多年研究后,其已被認為是當代心理測量和統計研究中較為重要的方向與內容。個體認知診斷由于可以呈現出個體的心理缺陷信息,適用于一對一教學模式,而并不適用于高校日常教學中的一對多的教學模式。高校教學中,應當選用群體認知診斷評估,通過研究群體的心理缺陷信息來制定適宜的心理輔導方案和策略。然而,現有群體認知診斷模型的診斷對象大多以個體為基礎,其診斷結果由個體(群體中)對屬性的掌握比例決定,判據不直觀且單一,難以針對性得進行補救教學[1?4]。此外,個體診斷給群體所帶來的誤差難以估計,且評估過程所需的時間、物力及人力成本較高,易造成不必要的浪費。因此,亟待研究并開發一種群體水平評估的認知診斷模型,從而對群體進行直接的認知診斷。本文基于G?AHM模型,研究并開發了一種群體水平評估的認知診斷模型。經Monte Carlo模擬和實證測試后發現,該認知診斷模型對群體水平認知診斷的效果良好。同時,其能夠為相關高校群體心理健康水平評估認知診斷模型的研究與開發提供支持。
1 ? 群體水平認知診斷模型的研究和開發
本文對群體水平評估認知診斷模型的研究,主要基于群體水平項目反應理論、規則空間模型(RSM)、Q矩陣理論(屬性階層模型AHM中),最終獲得的模型本文將其命名為群體水平的屬性階層模型(G?AHM)[5?9]。
1.1 ?G?AHM方法的基本概念

2 ?G?AHM模型的相關性能研究
2.1 ?研究目的和過程
為了探究本文G?AHM模型的性能、合理性和分類判別診斷方法的準確性與穩定性,選用模式判準率(PMR)、邊際判準率(MMR)及可允許出現一個失誤的模型判準率(OPMR)。通過考察統計數據中出現的失誤概率(ep)對診斷準確率進行評價。具體而言,選擇0,0.05,0.1,0.15從小到大共4個水平來代表失誤概率,總共進行4個實驗。
測試共涵蓋了20個項目,包含了7個考核屬性。數據以Monte Carlo模擬生成,并按照如下原則對Q矩陣進行隨機模擬:包含R矩陣;每個項目中被考核的屬性數量應當小于等于4個;每個屬性[10]應當被考核至少3次。該測試選擇了1 000個群體,其中每個群體中的作答人數對應各項目均是10人,依次按照理想作答(認知狀態賦值,得到理想作答)、觀察作答(按照ep取值產生觀察作答)、自編程序和30次重復后,計算獲得各個指標的均值。
2.2 ?結果和相關分析
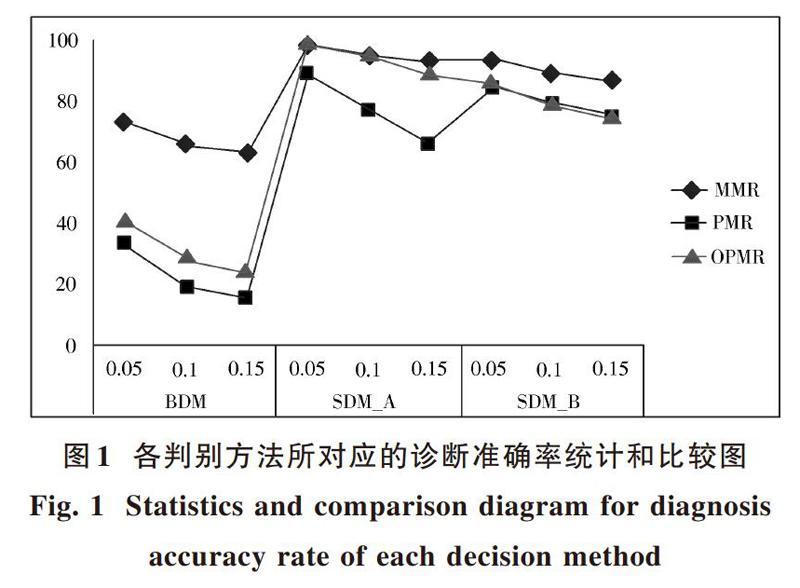
認知狀態診斷準確率的相關分析,如圖1所示。即為各判別方法所對應的,診斷準確率統計與比較圖。從中可知,各判別方法的判準率指標值總會隨著失誤數據(ep值)的增加而下降。具體而言,BDM在觀察作答上相較于SDM判別法具有較低的診斷準確率,這與文獻[11]中敘述的個體診斷模型的結果相吻合。此外,SDM_A判別方法的MMR和OPMR均大于90%,要遠優于SDM_B判別方法,且隨著ep的增加優勢越發明顯;而SDM_B判別方法則在PMR上有較大的優勢。
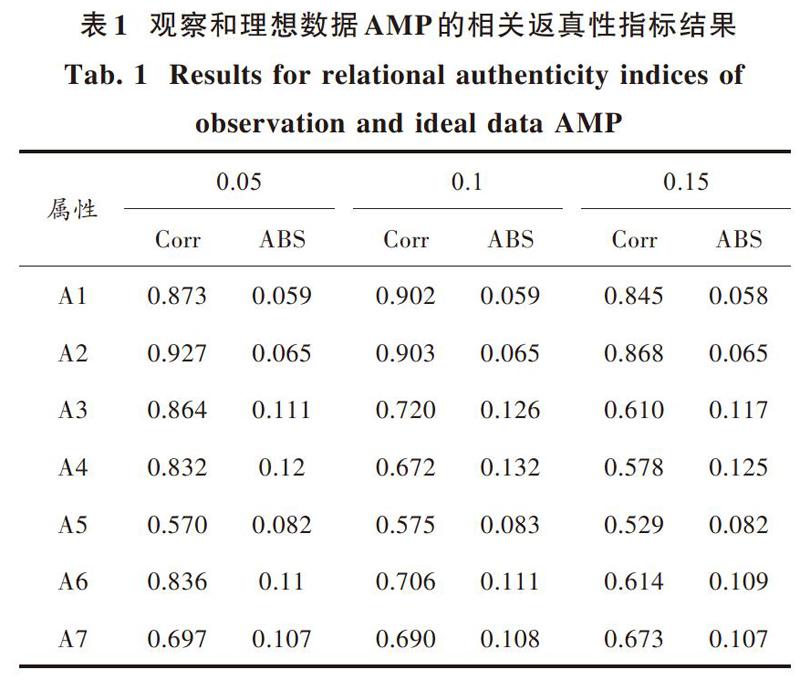
對于屬性掌握概率診斷的結果和相關分析,可見下表1所示,即觀察和理想數據AMP的相關返真性指標結果(包括Corr皮爾遜相關系數以及ABS平均絕對離差)。易知,在0.05水平上,絕大多數的相關系數均較為顯著,且隨著ep值的增加而存在一定幅度的下降;此外,ABS值在各個屬性中沒有過大的變化,總體保持穩定。
總體來看,G?AHM模型具有較好的可行性和合理性。SDM判別法及對應的AMP結果的穩定性與診斷精度良好,且SDM_A方法在MMR和OPMR方面均具有較大的優勢。而SDM_B方法則在PMR方面有較高的準確率。
3 ?G?AHM對心理狀況的群體認知診斷評估
3.1 ?研究目的和過程
為了評估高校學生心理狀況的群體診斷,并洞察心理認知發展過程中的相關群體特征以及可能存在的認知問題,本文使用了文獻[10]中的實際材料和數據對G?AHM模型進行相關測試。該材料具有7個互相無結構層級關系的屬性(A1~A7依次分別對應記憶、注意、感知、知識表征、推理、創造力以及問題解決的運作)和20個項目。測試過程中,本文在群體的認知診斷中選用了模型中的SDM_A方法,并與文獻[10]的結果進行比較。
3.2 ?結果和相關分析
從表2的頻數分布表和分析中可知,即使理想狀態下的認知狀態應有128種,實際各學校經診斷后表現的認知狀態只有14種。從文獻[10]中獲知,個體診斷結果中學生產生這14種認知狀態的比例較高(達到63.5%)。由此說明,個體共性部分的認知狀態會保留在群體認知狀態中,并在群體認知診斷中體現出來。

此外,70%的學校存在1111001,1111010,1111101和1111110的認知狀態。具體而言,學生未能掌握A5,A6以及A7中的一到兩個屬性。對每個屬性的掌握比例進行統計和分析,可以發現A3和A4屬性掌握較好,幾乎所有學校的學生均可掌握;而A1和A2屬性的掌握最差,僅有約10%的學生能夠較好的掌握;此外,A5~A7屬性的掌握也較差,只有略大于30%的學校學生能較好掌握。值得注意的是,學校的能力及屬性掌握概率和以個體診斷為基礎獲得的屬性掌握比例具有較強的相關性(分別為0.865和0.859)。從中可以反映該模型的效度較高,能與以個體為基礎的群體診斷結果相吻合。
從表3中可以獲知,A2~A4屬性具有較高的準確應用水平(A4最高)。其次是A1,A6和A7,最差的是A5屬性,其已經出現了較大的兩極分化趨勢,需要特別注意。總體來看,各學校反映出的心理認知缺陷主要表現在推理、創造力以及問題解決的運作上,學校應針對性地對學生進行相關的心理輔導。

4 ?結 ?語
目前群體認知診斷模型大多以個體為診斷對象,這會使診斷結果誤差較大,且需要耗費大量的人力、物力。為此,本文在G?AHM模型的基礎上,研究并開發了一種群體水平評估的認知診斷模型。該模型結合了GIRT、認知診斷模型的特點,具有診斷成本低、誤差小等優點。Monte Carlo模擬和實證測試表明,該認知診斷模型具有較好的穩定性以及較高的邊際判準率,且合理性與可行性較好,對群體水平認知診斷具有良好的效果,能對高校學生心理健康認知診斷提供有利的參考。
參考文獻
[1] TATSUOKA K K, CORTER J E, TATSUOKA C. Patterns of diagnosed mathematical content and process skills in TIMSS?R across a sample of 20 countries [J]. American educational research journal, 2004, 41(4): 901?926.
[2] BIRENBAUM M, TATSUOKA C, YAMADA T. Diagnostic assessment in TIMSS?R: between?countries and within?country comparisons of eighth graders′ mathematics performance [J]. Studies in educational evaluation, 2014, 30(2): 151?173.
[3] CARMI A Y, MOSKOVICH D. Computing with coloured tangles [J/OL]. [2015?07?21]. https://arxiv.org/pdf/1408.2685v3.pdf.
[4] HLINKA O, SLUCIAK O, HLAWATSCH F, et al. Distributed data fusion using iterative covariance intersection [C]// Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing. Florence: IEEE, 2014, 29: 1861?1865.
[5] LINDEN W J, HAMBLETON R K. Handbook of modern item response theory [M]. New York: Springer, 1997.
[6] MISLEVY R J. Item response models for grouped data [J]. Journal of educational statistics, 1983, 8(4): 271?288.
[7] TATSUOKA K K. Cognitive assessment: an introduction to the rule space method [M]. Abingdon: Routledge, 2009.
[8] LEIGHTON J P, GIERL M J, HUNKA S M. The attribute hierarchy method for cognitive assessment: a variation on tatsuoka′s rule?space approach [J]. Journal of educational measurement, 2010, 41(3): 205?237.
[9] MOSKOVICH D, CARMI A Y. Tales told by coloured tangles [J]. International journal of unconventional computing, 2015, 12(1): 1?29.
[10] 毛秀珍.基于屬性掌握概率的認知診斷模型[J].四川師范大學學報(自然科學版),2014,37(3):437?443.
MAO Xiuzhen. The attribute mastery probability cognitive diagnostic model [J]. Journal of Sichuan Normal University (Natural science), 2014, 37(3): 437?443.
[11] 周駿,徐淑媛,董圣鴻.以實質心理學為基礎的評估:認知診斷[J].心理學探新,2011,31(3):265?269.
ZHOU Jun, XU Shuyuan, DONG Shenghong. The assessment based on substantive psychology: cognitive diagnosis [J]. Psychological exploration, 2011, 31(3): 265?269.

