基于高斯核函數的K—means聚類在分布式下的優化

趙明明 張桂蕓 潘冬寧 王蕊

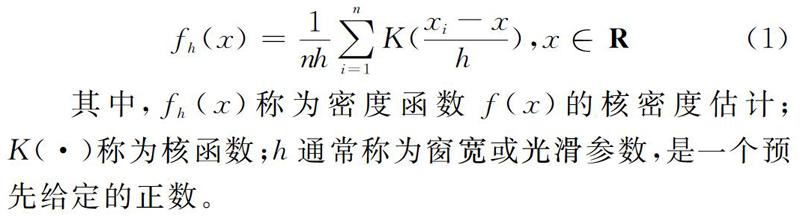
摘 要：隨著如今數據量的爆發式增長，傳統的數據挖掘方法已經遠遠不能滿足人們需求，K-means聚類作為一種經典的聚類算法，其應用領域很廣。但是K-means算法在隨機選取初始聚類K個中心時，容易使聚類結果不穩定，因此提出基于核函數的K-means聚類算法。與此同時，結合MapReduce分布式框架對改進后的K-means聚類算法作分布式計算。研究結果表明，基于高斯核函數的K-means聚類在分布式下的計算能夠加速K-means聚類過程，且結果優于單獨基于核密度估計的K-means算法。

關鍵詞：高斯核函數；K-means聚類；核密度；分布式

DOI：10.11907/rjdk.172480

中圖分類號：TP312

文獻標識碼：A 文章編號：1672-7800（2018）004-0064-03

Abstract：With the explosive increase of data， the traditional data mining has been far from being enough to meeting the needs of people. K-means clustering is a classical clustering algorithm， and its application field is very extensive. However， when the K-means algorithm randomly selects the initial clustering K centers， it is easy to make the clustering results unstable. Therefore， this paper proposes a K-means clustering algorithm based on kernel function. In this paper， the MapReduce distributed framework is used to do the distributed calculation of the improved K-means clustering algorithm. The results show that K-means clustering based on Gaussian kernel function can accelerate the process of K-means clustering in distributed calculation， and the result is better than K-means algorithm solely based on kernel density estimation.

Key Words：Gaussian kernel function； K-means clustering； distributed

0 引言

隨著科技的迅速發展，在工業、商業、醫療、工程、航天等各個領域產生了大量數據，數據規模已經從先前的GB上升到TB、PB乃至EB和ZB。據統計，在2020年全世界的數據規模將達到40ZB，相當于平均每人擁有5 247G的數據。因此，如何處理和管理如此龐大的數據是一項相當艱巨的任務，在數據量日益暴漲的場景下對客戶的精準推薦服務也面臨著嚴峻考驗。為了能夠從數據中獲取有價值的信息，各公司開始對龐大的數據進行挖掘與分析。

K-means聚類算法是數據挖掘領域最重要的經典算法之一，與其它數據挖掘方法相比，聚類不需要先驗知識即可完成數據的分類。聚類算法可以分為基于劃分、密度、模型等多種類型[1]。然而在面對大規模數據時，K-means算法表現不夠理想，并且在初選K值時非常困難。針對K-means的聚類數目K值難以確定和高維大數據集上的運算效率問題，本文設計了一種新型聚類算法，并且提出一種基于高斯核函數的K-means聚類在分布式下的優化算法。核函數估計又稱為核密度估計（Kernel Density Estimate，KDE），是一種非參數估計方法，不需要預知數據集分布，是一種在未知數據集分布情況下進行聚類的有效方法。因此，可以采用核函數估計的方法處理高維度數據。另外Hadoop上的MapReduce框架能夠快速、準確、高效地處理大量數據，所以采用MapReduce框架又可以解決在單機上運行效率低的問題。本文提出將建立好的模型運用在MapReduce分布式框架下運行。實驗結果表明，該方法在不影響聚類結果的情況下，有效縮短了聚類過程所需的時間。

1 核函數估計

在給定樣本集合求解隨機變量的分布密度函數時會經常用到兩種估計，分別是參數估計和非參數估計。由于參數模型的缺陷，Rosenblatt和Parzen提出了非參數估計方法，即核密度估計方法。由于核密度估計方法不利用有關數據分布的先驗知識，對數據分布不附加任何假定，是一種從數據樣本本身出發研究數據分布特征的方法，因而在統計學理論和應用領域均受到高度重視[2]。

總體而言，核函數就是將輸入空間映射到高維的特征空間，然后再在高維的數據空間進行數據處理。這種映射是非線性變換的，才能將輸入空間映射出不同特征的高維空間。

其中，fh（x）稱為密度函數f（x）的核密度估計；K（·）稱為核函數；h通常稱為窗寬或光滑參數，是一個預先給定的正數。

通過以上定義可以得出，分布密度函數的核密度估計f不僅與給定的數據樣本集有關，還與核函數的選擇與窗寬參數h的選擇有關[3]。理論上而言，窗寬h隨著n的增大而減小，即當n趨近于∞時，h趨近于0。如果h取值較大，然后x經過壓縮變換xi-xh后，突出了平均化，密度細節則會被淹沒，使估計出來的密度曲線過于平穩，導致結果分辨率過低；如果窗寬h值太小，隨機性的影響則會變大，從而形成一種非常不規則的曲線，導致密度的重要特性不會凸顯出來，最終造成密度估計波動性大，穩定性不好。所以要選擇一個合適的窗寬h值[4]。

如圖1所示，采用不同的窗寬h值進行核密度估計，h=2時曲線較為光滑，h=0.05時，對應的核密度估計曲線上下波動較為頻繁，并且這兩條曲線與真實曲線相差甚遠。圖中的虛線是實際概率密度曲線。在h=2與h=0.05之間取h=0.337，對應的KDE密度曲線更接近于實際概率密度函數曲線。

為了解決窗寬h的選取問題，需要引入積分均方誤差的概念。積分均方誤差可以判斷估計所得的概率密度函數（x）和真實概率密度函數f（x）存在的差異，其表達式為：

2 MapReduce

由于 Hadoop 沒有針對迭代計算作特殊優化，因此利用 Hadoop 的核心算法 MapReduce 進行K-means迭代設計[5]，將原有串行算法中每一次迭代計算過程對應一次MapReduce計算過程，以此完成數據點到鄰近簇中心的距離，然后把每一次迭代過程封裝成一個MapReduce作業K-meansJob。為了得到更優的聚類效果，需要創建多個K-meansJob。

圖2描述了基于高斯核函數估計的K-means聚類并行化計算流程：從HDFS上讀取數據集后進行高斯核密度估計，獲取數據集密度分布；然后由密度分布設定密度閾值和半徑閾值，由這兩個閾值獲取K值和初始聚類中心；把K值作為初始值輸入，然后啟動K-meansJob，每一次聚類都包括Map和Reduce兩部分，每個Reduce匯總一個簇的數據點集，然后計算更新該簇的中心點；每一次聚類結束后，都根據當前結果判斷是否收斂；如果聚類結果沒有滿足收斂條件，則Hadoop會再次創建K-meansJob，把上一次的輸出結果作為本次輸入；重復執行聚類任務，直到聚類結果滿足最大迭代次數或收斂條件為止。

3 實驗結果分析

本次實驗在經典K-means算法和本文算法上各實驗50次，每10次為一組求平均值，得出5組平均值。在經典K-means中對初始值非常敏感，并且迭代次數較多。然而本文算法先進行高斯核密度估計，然后再進行K-means聚類，這樣不用賦初始K值，并且移植到MapReduce分布式框架下的運行效率也大大提高。通過表1可以看出，本文算法相比于經典K-means算法，迭代次數少，誤差率低，運行結果的正確率也更高。

4 結語

針對傳統K-means聚類算法的初始K值選取困難，且對于高維大數據的聚類效果不太明顯，以及在傳統K-means有時會形成局部最優，而非全局最優的缺點，本文采用基于高斯核函數密度估計的方法在Hadoop平臺下進行K-means聚類。實驗結果顯示，本文算法明顯優于傳統的K-means聚類算法，并且運算效率也優于單機下運行高斯核密度估計的K-means聚類。

參考文獻：

[1] 翟東海，魚江，高飛，等.最大距離法選取初始聚類中心的K-means文本聚類算法的研究[J].計算機應用研究，2014，31（3）：713-715，719.

[2] ROSENBLATT M. Remarks on some nonparametric estimates of a density function [J]. The Annals of Mathematical Statistics，1956，27（3）：832-837.

[3] JONES M C， MARRON J S， SHEATHER S J. A brief survey of bandwidth selection for density estimation [J]. Journal of the American Statistical Association，1996，3（433）：401-407.

[4] 楊茹.核函數的密度估計算法[D].哈爾濱：哈爾濱理工大學，2016.

[5] 江小平，李成華，向文，等.K-means 聚類算法的MapReduce并行化實現[J].華中科技大學學報：自然科學版，2011， 39（1）：120-124.

[6] 熊開玲，彭俊杰，楊曉飛，等.基于核密度估計的K-means聚類優化[J].計算機技術與發展，2017，27（2）：1-5.

[7] 雷小鋒，謝昆青，林帆，等.一種基于K-means局部最優性的高效聚類算法[J].軟件學報，2008，19（7）：1683-1692.

[8] 謝娟英，高紅超.基于統計相關性與K-means的區分基因子集選擇算法[J].軟件學報，2014，25（9）：2050-2075.

[9] MACQUEEN J B. Some methods for classification and analysis of multivariate observation [C].Proceedings of 5th Berkeley symposium on mathematical statistics and probability. California： University of California Press，1967：281-297.

[10] DUDOIT S，FRIDLY J.A prediction-based resampling method for estimating the number of clusters in a dataset [J]. Genome Biology，2002，3（7）：1-21.

[11] BUCH-LARSEN T， NIELSEN J P， GUILLEN M. Kernel density estimation for heavy-tailed distributions using the champernowne transformation[J]. Statistics，2005，39（6）：503-518.

[12] RASHMI C. Analysis of different approaches of parallel block processing for K-Means clustering algorithm[J]. Computer Science，2017.

[13] NIU B， DUAN Q， LIU J， et al. A population-based clustering technique using particle swarm optimization and k-means[J]. Natural Computing，2017，16：45-59.

（責任編輯：黃 健）