單脈沖測量雷達數據濾波算法研究

蔣立民

（91245部隊，遼寧葫蘆島，125000）

0 引言

數據處理系統是雷達系統的重要組成部分。數據處理系統在獲取雷達信號處理產生的測量數據后，對所收到的測量數據主要進行分析判斷、相關處理、濾波與預測、平滑、外推等，最終實現對目標的穩定連續跟蹤和對目標狀態的精確估計。其處理的關鍵技術在于測量數據組織、相關和濾波算法的實現。本文只針對其中的濾波處理進行了研究，濾波處理主要用于解決測量數據的不精確性和被測量目標狀態的跟蹤與預判，目前常用的濾波算法主要包括α-β濾波、Kalman濾波和最小二乘法，通過分析三種算法的原理，并比較其優點有助于實踐應用者在選擇算法時做出最合理的選擇。

1 濾波算法原理

1.1 最小二乘法

最小二乘法的濾波原理是：根據采集到的數據組(xi, yi)，其中i等于(1,2···,n)，選定近似函數形式，即給定函數類H，求解?(χ)∈ H ，即

使得式（1）為最小，即

通常在單脈沖雷達數據處理中一般選用多項式擬合對給定數組(xi?yi)求一個m(m＜n)次多項式，即

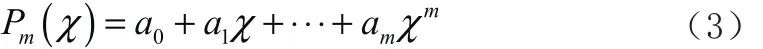
使得

為最小，選取參數 ai(i = 0 ,1,···,m )，使得

式（5）中，H為至多m次多項式的集合。Pm(χ)稱為這組數據的最小二乘m次擬合多項式。由多元函數取極值的必要條件，得

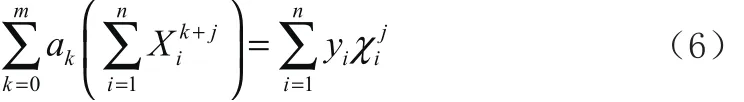
式（6）即是最小二乘擬合多項式的系數 ak( j =k = 0 ,1,···,m)應滿足的方程組，由函數組{1 , χ,χ2,· · ·,χm}的線性無關性可以得證式（6）存在唯一解，且解所對應的多項式 Pm(χ)必定是給定數組(xi, yi)的最小二乘擬合多項式。

1.2 Kalman濾波

在單脈沖雷達測量過程中，根據雷達獲得的前兩次測量值z1和 z2求得Kalman濾波的狀態初值，即……