基于猴群算法求解0-1背包問題①

徐小平,師喜婷,錢富才

1(西安理工大學 理學院,西安 710054)

2(西安理工大學 自動化與信息工程學院,西安 710048)

背包問題是由Merkel和Hellman在1978年提出的[1],它是一個典型的組合優化問題,屬于NP-hard難題,隨著問題規模越來越大,復雜度增強.在實際應用中,許多工業和金融等問題都可以用背包問題來描述,如預算控制、資源分配、項目選擇、資本投資、金融組合、材料切割和物件裝箱等[2].近年來,背包問題已成為眾多學者研究的一個熱點問題,尋找新的方法來求解背包問題具有重要的理論和實際意義[3].目前,求解背包問題的方法主要有兩種: 最優算法和啟發式算法.最優算法包括窮舉法、動態規劃法、遞歸算法、回溯法和分支界限法等[4–7].啟發式算法包括差分進化算法[8],粒子群算法[9]和遺傳算法[10]等.前者的思想比較簡單,不需要其它專業知識,一般適用于求解規模較小的問題; 后者一般適用于求解規模較大的問題,可是對其求解的精度還需繼續探討.

猴群算法是一種新興的群智能優化算法[11],該算法的突出特點在于求解高維的優化問題時,無需考慮函數是否可導或可微,只需要計算當前位置的偽梯度,就可以確定算法的搜索方向,并且該算法的結構簡單,參數少和易實現.因此,猴群算法在提出不久便得到了眾多學者的廣泛關注,在各個領域內得到了快速地發展,例如在大跨徑連續剛構橋傳感器優化布置問題[12]、入侵檢測系統存在高漏報率的問題[13]、加氣站項目進度的問題[14]、混合動力優化[15,16]、模糊規則的分類器[17]等領域.而文獻[12–17]中均是基本猴群算法的應用,可以看出在某種程度上解決了一些問題.但是,在上述問題的應用中,隨著測點數目或者規則等的增加,基本猴群算法暴露出易陷入局部最優,導致存在求解精度不高的弊端.因此,對該算法進一步研究是很必要的,并將其的應用進行擴展,來解決實際生活中的諸多應用問題具有重要的實際意義.

為了提高猴群算法的尋優性能,本文將誘導因子引入基本猴群算法的爬過程中,給出了一種誘導因子猴群算法,并將其應用到求解 0-1 背包問題.最后,通過仿真實驗驗證了該方法的可行性.

1 0-1 背包問題

0-1背包問題是一種常見的組合優化問題.一般可簡單敘述為: 設物品的數量為D,第i個物品的體積(重量)和價格分別為wi和pi,一個背包的能承受的最大容量為V,選擇一些物品,放入背包中.如何選擇物品,在滿足背包約束條件下,使背包中物品的總價值最大,這個問題被稱為0-1背包問題,其數學模型建立如下:

其中表示物品的價值向量,表示物品對應的體積(重量)向量,表示解向量.式(1)表示目標函數;式(2)中xi為決策變量,xi=0表示第i個物品未裝入包中,xi=1表示第i個物品裝入包中.

2 猴群算法

2.1 基本猴群算法

基本猴群算法是由Zhao和Tang兩位學者首次在期刊 Journal of Uncertain Systems 上提出的[11].該算法主要包括解的表示和初始化、爬過程、望過程和跳過程,其具體的操作過程如下:

Step1.解的表示和初始化: 設是目標函數的一個可行解,表示第i只猴子當前的位置,由式(3)生成.

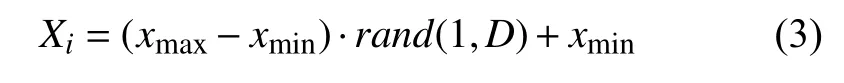
其中,M表示種群規模,D為維數,xij表示第i只猴子在第j維的位置,變量的區間為是由[0,1]之間的均勻分布的隨機數組成的D維向量.

Step2.執行爬過程: 爬過程是每只猴子在當前的范圍內通過逐步爬行迭代,尋找優化問題的目標函數值的過程,具體過程如下:

2) 計算其中,是目標函數所在位置的偽梯度.

3) 令其中,sign為符號函數.

4) 如果向量在范圍內,并且更新Xi為Yi: 否則,Xi不變.

5) 重復 1)–4),直到達到預定的執行次數Nc.

Step3.執行望過程: 在爬過程之后,每只猴子都到達了各自所在的山峰的頂端,并向四周眺望,觀察視野范圍內是否存在比當前位置更高的山峰.若存在,就從當前位置跳到更高的位置.具體過程如下:

1) 在視野范圍內隨機產生實數yij,令那 么其中,b為視野長度,它決定了猴子從當前位置眺望的最遠距離.

2) 如果向量的范圍內,并且更新Xi為Yi; 否則,重復1),直至找到可行的Yi.

3) 以Y作為初始位置,執行爬過程.

Step4.執行跳過程: 它的主要目的是由當前區域轉移到新的區域進行搜索.選擇所有猴子的重心位置作為支點,每只猴子從當前位置朝著支點的方向跳到新的區域進行搜索,具體過程如下:

1) 在跳區間[c,d]內隨機生成一個實數θ.

2) 令:

其中,其中被稱為支點.

3) 如果向量范圍內,并且更新Xi為Yi; 否則,重復1)和2),直至找到可行的Yi.

Step5.終止條件: 重復 Step2–Step4,直到達到預先設定的迭代次數N,算法終止,輸出結果.

2.2 誘導因子猴群算法

在基本猴群算法中,爬過程是非常重要的,它是控制算法的搜索精度.可是,在基本猴群算法中,猴群位置在爬過程中的更新,是沒有規律的,往往具有很大的隨機性,使得算法很難找到局部范圍內的最優個體,從而不容易找到全局最優個體,這樣就降低了算法的求解精度.

為了克服算法的這個缺陷,本文在爬過程中引入誘導過程,提出了一種誘導因子猴群算法.具體為: 在猴子爬行過程中,給定猴子向上爬行的指示,誘導它們向最優位置的方向爬行,這樣可以避免繞路,盡快找到局部范圍內的最優個體,從而迅速找到全局最優個體,來提高算法的尋優能力,達到提高算法的精度,其具體操作如下.

在爬過程中,隨機生成爬向量其中,分量由下述過程生成.

隨機生成一個M×D階矩陣其 中 ,分 量βi j是在區間[0,1]上隨機生成的一個實數.當時,否則,這樣,分量就可由下式(6)來表示.

這樣,在猴子爬行的過程中,就可以通過爬向量中0的個數來誘導猴子的爬行,來提高算法的尋優能力,進而達到提高算法的求解精度.其中,M為種群規模,D為維數,Nc為爬過程中爬的次數,kc為每次爬行的迭代次數,參數為猴子的爬步長.

在爬過程中引入誘導過程時,為了達到提高算法尋優能力的目的,那么就需要選擇一個合適的誘導次數.如果誘導次數過低,提高算法尋優能力就不太明顯.如果誘導次數過高,算法往往會出現陷入局部最優,達不到提高算法尋優能力的目的.因此,本文經過多次仿真后,找到當誘導次數時,既可以提高局部尋優能力,又可以避免因過高的局部尋優能力而降低了全局尋優能力,從而提高了算法的尋優性能.

3 利用誘導因子猴群算法求解0-1背包問題

利用誘導因子猴群算法求解0-1背包問題時,就是以式(1)作為目標函數,尋找式(1)的最大值.在求解中,它們的對應關系為: 每只猴子的位置,相當于式(1)的一組可行解; 猴群規模對應可行解的個數; 維數對應物品的數量.實施步驟如下.

Step1.參數值設定,如種群規模M=20,最大迭代次數等.

Step2.隨機生成一個二進制向量作為初始位置(其中,第i位為1表示第i件物件被選中,若為0,則表示第i件物件未被選中).并計算所有猴子的目標函數值找出較優位置.

Step3.執行爬過程,計算,產生新的二進制向量若則更新第i只猴子當前的位置,即直到預定的執行次數Nc.然后,為了能夠優先選取物品中單位體積價值較高的裝入背包,在這里設計一個誘導因子,具體過程如下.

① 求出每件物品的單位體積的價值量,第i件物品為:

② 求出每件物品所占背包的比例,第i件物品為:

③ 據此設計誘導因子為:

其中,α為常量,用來調整的關系.

④ 隨機選取兩個值c1和c2,其中,如果并且則更新猴子的位置的變量為否則更新為計算若則更新第i只猴子的位置.直到一定的誘導次數guide.

Step4.執行望過程,在視野范圍內生成新的二進制向量并計算則更新第i只猴子當前的位置,即

Step5.執行跳過程,計算,產生新的二進制向量計算計算若則更新第i只猴子當前的位置,即

Step6.重復 Step3–Step5,直到達到預定的最大迭代次數nMax,算法結束,輸出最優個體和最優值.

4 實例仿真及其分析

為了驗證所給算法的可行性,下邊給出兩個算例,它們的規模由小變大,具體數據見以下相關算例數據.比較差分進化算法 (Differential Evolution Algorithm,DEA)[8]、粒子群算法 (Particle Swarm Optimization,PSO)[9]、遺傳算法 (Genetic Algorithm,GA)[10]、基本猴群算法 (Basic Monkey Algorithm,BMA)[11]以及本文所給誘導因子猴群算法 (Inducing Factor Monkey Algorithm,IFMA)求解問題的效果.

算例 1.物品數量n=50,背包容量V=1000,物品價值R=[220,208,198,192,180,180,65,162,160,158,155,130,125,122,120,118,115,110,105,101,100,100,98,96,95,90,88,82,80,77,75,73,72,70,69,66,65,63,60,58,56,50,30,20,15,10,8,5,3,1],物品重量W=[80,82,85,70,72,70,66,50,55,25,50,55,40,48,50,32,22,60,30,32,40,38,35,32,25,28,30,22,50,30,45,30,60,50,20,65,20,25,30,10,20,25,15,10,10,10,4,4,2,1].

算例 2.物品數量n=100,背包容量V=2010,物品價值R=[68,101,125,159,65,146,28,92,143,37,5,154,183,117,96,127,139,113,100,95,12,134,65,112,69,45,158,60,142,179,36,43,107,143,49,6,130,151,102,149,24,155,41,177,109,40,124,139,83,142,116,59,131,107,187,146,73,30,174,13,91,37,168,175,53,151,125,31,192,138,88,184,110,159,189,147,31,169,192,56,160,138,84,42,151,37,21,22,200,85,135,200,139,189,68,94,84,22,18,115],物品重量W=[42,35,70,79,63,6,82,62,96,28,92,3,93,22,19,48,72,70,68,36,4,23,74,42,54,48,63,38,24,30,17,91,89,41,65,47,91,71,7,94,30,85,57,67,32,45,27,38,19,30,34,40,5,78,74,22,25,71,78,98,87,62,56,56,32,51,42,67,8,8,58,54,46,10,22,23,7,14,1,63,11,25,49,96,3,92,75,97,49,69,82,54,19,1,28,29,49,8,11,14].

在仿真中,用本文所給IFMA求解上述問題時,算法的參數設定為: 種群規模M=20,最大迭代次數nMax=500,爬步長a=1,爬的迭代次數Nc=20,誘導次數guide=5,視野長度b=0.5,望的迭代次數Nw=3,跳區間常量α=1.2.

利用上述五種算法分別對算例1和算例2進行一次求解,得到算例1的最優值和最優個體羅列在表1,尋優過程如圖1所示,算例2的最優值和最優個體羅列在表2,優化過程曲線如圖2所示.

表1 算例 1 的最優值和最優個體

表2 算例 2 的最優值和最優個體

接著,進一步利用這5種算法分別對算例1和算例2進行50次求解,得出它們的最優值、最差值、平均值和方差分別羅列在如表3和表4.

表3 算例 1 的結果

表4 算例 2 的結果

通過以上仿真結果中的圖1,圖2和表1至表4可以看出,文中在BMA算法中的爬過程中引入誘導過程后,很好地誘導了猴子向著指定的方向爬行,從而避免了算法走彎路,提高了算法的局部尋優能力和全局尋優能力.而且隨著物品數量的增大,復雜度的增強,相對于 DEA,PSO,GA 和 BMA 算法,所給 IFMA 算法的求解精度仍然較高,且方差較小.從而說明所給IFMA算法具有較高的可行性和穩定性,達到了預期的效果,為求解0-1背包問題提供了新的途徑.

5 結束語

在利用猴群算法求解0-1背包問題時,在爬過程中,引入誘導因子后,可以誘導猴子向著指定的方向爬行,從而避免繞路,使得所給IFMA能夠找到全局最優解.通過仿真實驗表明,利用所給的IFMA求解0-1背包問題達到了預期的結果,提高了求解精度.

圖1 算例 1 優化過程曲線

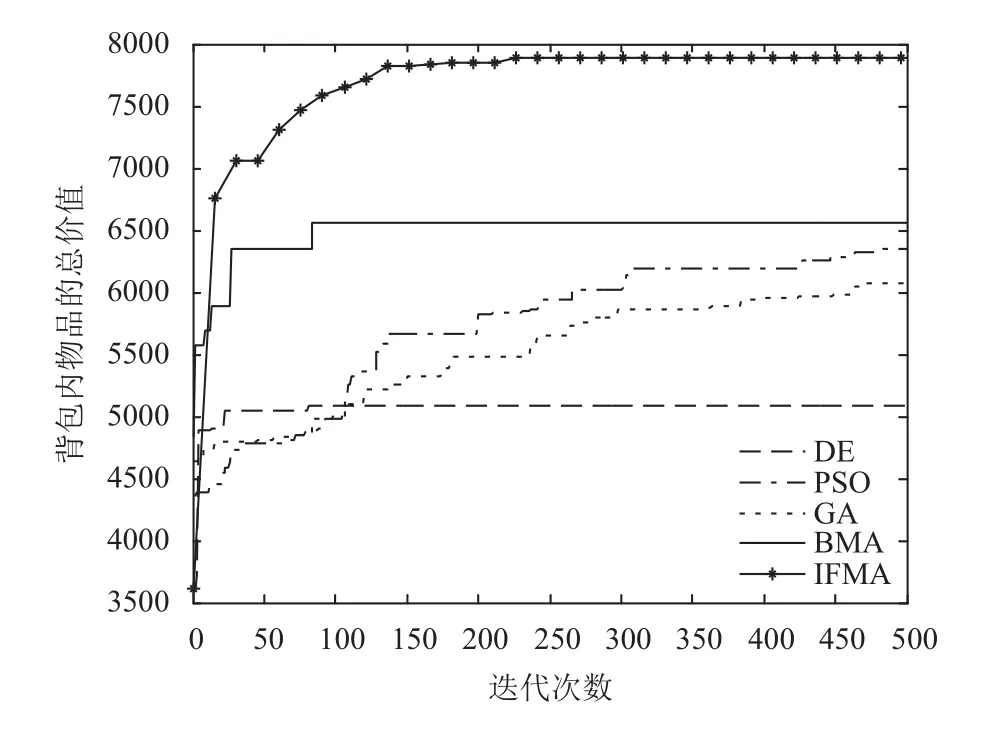
圖2 算例 2 優化過程曲線

參考文獻

1Merkle R,Hellman M.Hiding information and signatures in trapdoor knapsacks.IEEE Transactions on Information Theory,1978,24(5): 525–530.[doi: 10.1109/TIT.1978.1055 927]

2趙學武,劉向嬌,王興,等.求解 0-1 背包問題的遺傳算法.南陽師范學院學報,2014,13(6): 21–25.

3Srinivasan V,Varghese G.Fast address lookups using controlled prefix expansion.ACM Transactions on Computer Systems,1999,17(1): 1–40.[doi: 10.1145/296502.296503]

4李鳴山,鄭海虹.0-1背包問題的多重分枝－限界算法.武漢測繪科技大學學報,1995,20(1): 83–87.

5寧愛兵,馬良.0/1背包問題快速降價法及其應用.系統工程理論方法應用,2005,14(4): 372–375.

6王粉蘭,孫小玲.不可分離凸背包問題的拉格朗日分解和區域分割方法.運籌學學報,2004,8(4): 45–53.

7王樂,王世卿,張靜樂.基于 Matlab 的 0-1 背包問題的動態規劃方法求解.計算機技術與發展,2006,16(4): 88–89,92.

8荊源.背包問題的差分進化算法.才智,2011,(7): 92–93.

9趙傳信,季一木.粒子群優化算法在0/1背包問題的應用.微機發展,2005,15(10): 23–25.[doi: 10.3969/j.issn.1673-629X.2005.10.009]

10樂天.遺傳算法求解0/1背包問題的綜述.浙江海洋學院學報 (自然科學版),2013,32(1): 71–74.

11Zhao RQ,Tang WS.Monkey algorithm for global numerical optimization.Journal of Uncertain Systems,2008,2(3):164–176.

12李曉,倪富陶,孫維剛,等.基于猴群算法的連續剛構橋傳感器優化布置研究.公路,2016,61(3): 65–69.

13張佳佳,張亞平,孫濟洲.基于猴群算法的入侵檢測技術.計算機工程,2011,37(14): 131–133.[doi: 10.3778/j.issn.1002-8331.2011.14.037]

14趙濤,夏雨,宗瑪利.基于猴群算法的加氣站項目進度研究.價值工程,2010,29(8): 90–92.

15申彩英,高韜.基于猴群算法的混合動力汽車能量管理策略 .計 算 機 工 程 與 應 用 ,2014,50(14): 9 –13,120.[doi:10.3778/j.issn.1002-8331.1308-0015]

16Ituarte-Villarreal CM,Lopez N,Espiritu JF.Using the monkey algorithm for hybrid power systems optimization.Procedia Computer Science,2012,(12): 344 –349.[doi: 10.1016/j.procs.2012.09.082]

17Hodashinsky IA,Samsonov SS.Design of fuzzy rule based classifier using the monkey algorithm.Mathematical Methods and Algorithms of Business Informatics,2017,1(39): 61–67.