基于KPCA和投影字典對學(xué)習(xí)的人臉識別算法①

鄧道舉,李秀梅

(杭州師范大學(xué) 信息科學(xué)與工程學(xué)院,杭州 311121)

當(dāng)前,稀疏表達(dá)理論在圖像識別中越來越受到人們關(guān)注[1,2].2009 年,Wright等人提出了基于稀疏表達(dá)分類SRC的人臉識別方法[3],稀疏表達(dá)是利用字典中的原子線性表示信號的一種方法,它通過稀疏編碼和重構(gòu)分類兩步來解決識別問題.2013年,張磊等人提出了基于聯(lián)合表達(dá)分類CRC的識別方法[4].研究指出,在SRC方法中對識別率的貢獻(xiàn)起到關(guān)鍵性作用的并非求稀疏約束的L1范數(shù)最小化算法,而是聯(lián)合表達(dá).在保證識別率的前提下,為了提高識別速度,引入了正則化最小平方法替代原SRC方法中的L1范數(shù)最小化算法.其中,字典在稀疏表達(dá)和聯(lián)合表達(dá)中具有重要作用,分析字典[5]和綜合字典[5]是最常用的字典.分析字典能快速實(shí)現(xiàn)稀疏編碼,但不能有效表達(dá)復(fù)雜的局部信息.綜合字典能有效表達(dá)復(fù)雜局部信息,實(shí)現(xiàn)完美重構(gòu),但稀疏編碼速度較慢.

字典學(xué)習(xí)是設(shè)計(jì)或構(gòu)造字典[6,7]的一種重要方法.常用的字典學(xué)習(xí)算法有最優(yōu)方向法、K-SVD算法等[8].Yang等人提出了Metaface字典學(xué)習(xí)算法MFL[9]和線性判別字典學(xué)習(xí)算法FDDL[10],MFL和FDDL算法與K-SVD相比具有更強(qiáng)的表達(dá)能力.然而,MFL算法和FDDL算法利用綜合字典學(xué)習(xí)速度慢,不能實(shí)現(xiàn)大樣本快速識別任務(wù).

主成分分析PCA[11]在數(shù)據(jù)分析和模式識別中,通過計(jì)算數(shù)據(jù)的協(xié)方差矩陣來處理數(shù)據(jù),而協(xié)方差矩陣屬于二階統(tǒng)計(jì)特性,并未涉及到高階統(tǒng)計(jì)特性,因此做PCA變換后數(shù)據(jù)還會有高階冗余信息存在.此外,PCA只分析了數(shù)據(jù)間相關(guān)性,未對非相關(guān)性做分析.因此,PCA一般適用于線性數(shù)據(jù)和線性可分情況,而對于非線性數(shù)據(jù)和線性不可分問題,PCA往往滿足不了解決問題的需要.為了解決非線性問題,A Smola 等人提出了核主成分分析KPCA算法[12],運(yùn)用核方法,通過非線性映射將數(shù)據(jù)變換到某個高維特征空間后再做PCA分析.

本文提出了一種基于KPCA與DPL相結(jié)合的字典學(xué)習(xí)算法,即 K-DPL 算法.該算法利用核技術(shù),將數(shù)據(jù)樣本映射到高維空間(特征空間)以解決非線性問題,再進(jìn)行DPL訓(xùn)練,得到更具有判別性的字典以提高識別率和識別速度.最后針對ORL、擴(kuò)展YaleB、AR人臉庫,對本文提出的識別方法進(jìn)行性能分析與比較.

本文的其它部分安排如下: 第1節(jié)介紹了KPCA算法的主要實(shí)現(xiàn)過程和流形學(xué)習(xí)方法,第2節(jié)介紹了傳統(tǒng)字典學(xué)習(xí)模型與投影字典對學(xué)習(xí)DPL算法,第3節(jié)提出了將KPCA與DPL相結(jié)合的K-DPL算法,并介紹了及其實(shí)現(xiàn)步驟,第4節(jié)設(shè)計(jì)實(shí)驗(yàn)進(jìn)行了仿真驗(yàn)證,第5節(jié)進(jìn)行了總結(jié).

1 KPCA 算法

1.1 KPCA算法的主要過程

在人臉識別中,假設(shè): 每張人臉圖像是大小為的灰度矩陣,樣本數(shù)為N.將每張人臉圖像按列首尾連接拉成維數(shù)為d的列向量,則整個樣本集X表示為大小為其中第i張人臉圖像記為

定義一個映射其中將樣本映射到維數(shù)為D的高維空間中.將人臉圖像映射到該空間,得中心化后的樣本數(shù)據(jù)滿足設(shè)C表示中心化的樣本數(shù)據(jù)協(xié)方差矩陣,那么,從而得式 (1):

其中分別表示C的特征值和對應(yīng)的特征向量,并且可以證明: 任意一個特征向量均可由張成的空間線性表示,即,存在常系數(shù)滿足式(2):

將式(1)等號兩邊同時左乘將式(2)帶入(1)中,得式 (3):

將等式(3)兩邊同時進(jìn)行化簡,得式(4):

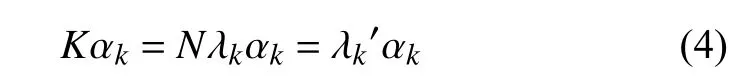
其中,表示中心化的核矩陣,也稱為核函數(shù),表示核函數(shù)K的第k個特征向量,表示K的特征值.

最后,根據(jù)K與C的特征值和特征向量關(guān)系式(5):

即可求出C的特征值和特征向量.

1.2 核函數(shù)類型

根據(jù)核函數(shù)的性質(zhì),可以劃分為如下4種常用類型:

(1) 線性核函數(shù):

(2) 高斯核函數(shù):

(3) 多項(xiàng)式核函數(shù):

(4) Sigmoid 核函數(shù):

其中,為各核函數(shù)對應(yīng)的參數(shù),可以根據(jù)不同的問題和數(shù)據(jù)選擇上述核函數(shù)并調(diào)整這些參數(shù),從而在模式識別等問題中達(dá)到最佳的模型.具體核函數(shù)及參數(shù)的選擇往往依據(jù)多次實(shí)驗(yàn)的效果來確定和調(diào)整.針對后文提出的算法,為了達(dá)到最佳識別表現(xiàn),實(shí)驗(yàn)時本文將分別選擇線性核、高斯核與多項(xiàng)式核作為核函數(shù).

1.3 流形學(xué)習(xí)

KPCA是將低維空間數(shù)據(jù)映射到高維空間后進(jìn)行PCA降維的特征提取方法.它能夠提取出一些線性不可分的信息,便于后續(xù)的識別分類.流形學(xué)習(xí)[13,14]也是特征降維的一類方法,它將高維的數(shù)據(jù)映射到低維,使該低維的數(shù)據(jù)能夠反映原高維數(shù)據(jù)的某些本質(zhì)結(jié)構(gòu)特征,這些高維數(shù)據(jù)實(shí)際上是一種低維的流形結(jié)構(gòu)嵌入在高維空間中.它分為線性和非線性兩種.其中,線性流形學(xué)習(xí)包括PCA與多維尺度變換MDS[15].與KPCA的作用類似,非線性流形學(xué)習(xí)也屬于非線性降維方式,其代表性方法有局部線性嵌入LLE[16]、等距映射Isomap[17]、拉普拉斯特征映射LE[18]等.上述方法在運(yùn)用中已經(jīng)取得了一些不錯的效果.然而,在人臉識別中還存在許多方法不收斂、采樣密度與采樣方式選擇以及降低維數(shù)不確定等問題,這些問題都會對最終的識別準(zhǔn)確性和識別速度產(chǎn)生較大影響.

2 投影字典對學(xué)習(xí)算法

2.1 傳統(tǒng)字典學(xué)習(xí)模型

傳統(tǒng)的字典學(xué)習(xí)算法是運(yùn)用稀疏表達(dá)對過完備字典學(xué)習(xí)一個綜合字典,而稀疏表達(dá)涉及稀疏系數(shù)或稀疏矩陣的求解.其模型描述如下.

假設(shè)有K類訓(xùn)練樣本,每個樣本的維數(shù)為d,整個訓(xùn)練樣本集其中表示第i類訓(xùn)練樣本子集,n為每類樣本數(shù).則大多數(shù)傳統(tǒng)字典模型框架為:

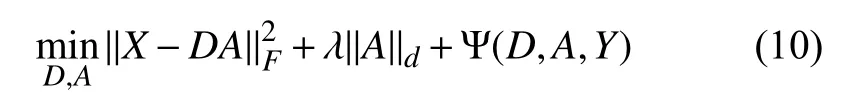
然而,利用L0或L1范數(shù)最小化求解具有判別性的編碼稀疏矩陣A的方法的時間代價很高,在識別問題中,不能滿足快速識別的要求.針對這一問題,Gu 等人提出了一種新的字典學(xué)習(xí)模型——投影字典對學(xué)習(xí)DPL[19].

2.2 投影字典對學(xué)習(xí)DPL

假設(shè)可以找到某個分析字典使得編碼A可通過分析得到,那么,X的表達(dá)會變得非常高效.基于這一思想,通過同時學(xué)習(xí)分析字典Q和綜合字典D,得到DPL的模型如下[19]:

其中為標(biāo)量為整個訓(xùn)練集X中去除后部分為綜合字典D的第i個原子.

3 基于KPCA的投影字典對學(xué)習(xí)算法K-DPL

由KPCA算法的原理可知,KPCA算法首先通過非線性映射將線性不可分的樣本投影到某個高維空間,使得樣本線性可分,然后再對該空間內(nèi)的樣本進(jìn)行PCA分析.而人臉圖像的某些信息是線性不可分的,比如某些局部紋理信息.通常,提取到的信息越好往往越有利于后續(xù)的識別工作.因此,單純地利用PCA來對人臉圖像分析往往未能對圖像的線性不可分類的信息進(jìn)行分析,從而影響識別效果.而DPL算法打破了傳統(tǒng)字典學(xué)習(xí)算法對稀疏表達(dá)的依賴,不僅提高了識別率,識別速度更是大幅提升.基于這兩方面,為了進(jìn)一步提高DPL的識別性能,本文提出了一種將KPCA與DPL相結(jié)合的算法,即K-DPL.

3.1 K-DPL算法

算法.K-DPL 算法

輸入: 對訓(xùn)練人臉樣本進(jìn)行K P C A特征提取,得到降維后的K類訓(xùn)練樣本 選擇測試人臉樣本y,分別設(shè)定參數(shù)λ、τ、m、γ輸出: 分析字典 Q,綜合字典 D① 固定 Q和 D,更新A:A?=a r g m i n A =1∥X k?D k A k∥2 F+τ∥Q k X k?A k∥2 F∑K k (1 3)可將上式最小二乘問題轉(zhuǎn)化為下式求解:A?k=(D T k D k+τ I)?1(τ Q k X k+D T k X k) (1 4)② 固定 A,更新 Q和 D:?Q的解可通過下式獲得:Q?k=τ A k X T k(τ X k X T k+λ X′k X′T k+γ I)?1.(1 7)其中,γ為一個很小的常數(shù).從第1類到第K類,利用式(1 4)、(1 7)、(1 6)分別更新 、 、A(t)k Q(t)k.D(t)k i d e n t i t y(y)=a r g m i n ③ 判定: ,當(dāng)相鄰兩次迭代結(jié)果差值小于某個閾值,則循環(huán)結(jié)束,輸出判定結(jié)果; 反之, ,返回上一步.i ∥y?D i Q i y∥2 t=t+1

4 實(shí)驗(yàn)

本實(shí)驗(yàn)分為三部分: 第一部分是將DPL算法與MFL、SRC、CRC、FDDL算法進(jìn)行比較,驗(yàn)證DPL的有效性和優(yōu)越性; 第二部分是將本文提出的KDPL與DPL、PCA降維后的DPL進(jìn)行比較,分析KDPL的識別性能; 第三部分是驗(yàn)證K-DPL對有光照變化和遮擋的人臉識別的有效性.第一、二部分在ORL人臉庫上測試.第一部分實(shí)驗(yàn)選擇每一類樣本中前5個人臉圖片作為訓(xùn)練樣本,后5個人臉圖片作為測試樣本.第二部分實(shí)驗(yàn)分別設(shè)置訓(xùn)練比例為0.1、0.3、0.5、0.7進(jìn)行實(shí)驗(yàn).第三部分在擴(kuò)展YaleB人臉庫和 AR 人臉庫上測試.實(shí)驗(yàn)環(huán)境為: Matlab 2015b,Intel i3-2350M 2.30 GHz,6 G 內(nèi)存.

ORL人臉庫中共有40個人的正面照,每個人有10張大小均為112×92像素的灰度圖片,每張圖片的主要區(qū)別在于表情和姿勢的變化.ORL人臉庫的部分圖像如圖1所示.

擴(kuò)展YaleB人臉庫中共有38個人的正面照,包含9種姿勢下的64種不同光照變化.擴(kuò)展YaleB人臉庫的部分圖像如圖2所示.

圖1 ORL 人臉庫部分圖像

圖2 擴(kuò)展 YaleB 人臉庫部分圖像

AR人臉庫中共有126個人的正面照,總計(jì)有4000 張.選取其中 50 名男性,50 名女性作為樣本.每人有26張大小均為165×120像素的灰度圖片,每張圖片的主要區(qū)別在于光照變化、墨鏡和圍巾遮擋.AR人臉庫的部分圖像如圖3所示.

圖3 AR 人臉庫部分圖像

4.1 DPL與MFL、SRC、CRC、FDDL算法比較

本實(shí)驗(yàn)首先將ORL人臉庫中每張訓(xùn)練樣本和測試樣本照片按照像素拉成10 304×1的向量,然后下采樣至1024×1的列向量,得到處理后的訓(xùn)練樣本和測試樣本進(jìn)行實(shí)驗(yàn)分析.為了達(dá)到最好的識別效果,實(shí)驗(yàn)參數(shù)設(shè)置為:迭代次數(shù)為20次.為了降低識別引入的誤差,每組實(shí)驗(yàn)進(jìn)行5次實(shí)驗(yàn),取其平均識別率和時間.實(shí)驗(yàn)結(jié)果如表1所示.

表1 在 ORL 庫上的識別結(jié)果比較

由表1可知,在ORL庫上,DPL算法實(shí)現(xiàn)人臉識別相比表中其他算法的識別率具有很大競爭力,而且,相比MFL、FDDL等利用稀疏編碼求解訓(xùn)練字典的算法,DPL具有訓(xùn)練速度快,測試耗時短的優(yōu)點(diǎn).

4.2 K-DPL算法與DPL、P-DPL比對

4.2.1 ORL 人臉庫上的實(shí)驗(yàn)與分析

為了提高DPL算法的識別率和識別速度,驗(yàn)證本文提出的K-DPL算法的有效性和優(yōu)越性,將KDPL與DPL、PCA降維后的DPL進(jìn)行比較,分別在訓(xùn)練比例為0.1、0.3、0.5、0.7的ORL人臉庫上進(jìn)行,表示為: ORL(1)、ORL(3)、ORL(5)、ORL(7),其中括號里的數(shù)表示訓(xùn)練樣本數(shù).每種訓(xùn)練比例下均進(jìn)行5次實(shí)驗(yàn)取平均識別率和識別時間.這里K-DPL算法的核函數(shù)選擇線性核函數(shù),而將PCA降維后的DPL表示為 P-DPL.實(shí)驗(yàn)參數(shù)設(shè)置為:取每個庫的訓(xùn)練樣本數(shù).ORL(1)庫上核函數(shù)選擇的是線性核函數(shù),核函數(shù)的參數(shù)其他庫上核函數(shù)選擇多項(xiàng)式核函數(shù),核函數(shù)的參數(shù)迭代次數(shù)在 ORL(1)、ORL(3)、ORL(5)、ORL(7)庫上分別為8、4、3、2.實(shí)驗(yàn)所得識別率如表2所示.

表2 不同訓(xùn)練比例下識別率 (%)

識別所需訓(xùn)練時間和測試時間分別如表3.

表3 不同訓(xùn)練比例下訓(xùn)練時間和測試時間比較(s)

由表3可知,本文提出的K-DPL算法訓(xùn)練和測試的速度比DPL算法的大約快20倍,和P-DPL相當(dāng).而在不同訓(xùn)練比例下,K-DPL的識別率均高于DPL和PDPL.因此,本文提出的K-DPL算法進(jìn)一步提升了DPL算法的識別速度和識別率.訓(xùn)練字典的效果圖如圖4所示.

圖4 訓(xùn)練字典的效果圖

4.3 擴(kuò)展YaleB和AR人臉庫上的實(shí)驗(yàn)與分析

實(shí)驗(yàn)所用擴(kuò)展YaleB人臉庫大小為504×2414,整個訓(xùn)練樣本大小為504×1216,整個測試樣本大小為504×1198.這里所用擴(kuò)展YaleB人臉庫為Jiang博士所提供,下載網(wǎng)址為: http://www.umiacs.umd.edu/ ～zhuolin/projectlcksvd.html.實(shí)驗(yàn)中,設(shè)置參數(shù)如下:核函數(shù)選擇的是高斯核函數(shù),核函數(shù)的參數(shù)設(shè)置為迭代次數(shù)為20.AR人臉庫上的實(shí)驗(yàn),首先將AR庫裁剪為大小504×2600樣本數(shù)據(jù),再將其為訓(xùn)練和測試兩部分.其中每類訓(xùn)練樣本20個,測試樣本6個.整個訓(xùn)練樣本大小為 504×2000,整個測試樣本大小為 504×600,實(shí)驗(yàn)參數(shù)設(shè)置為:核函數(shù)選擇的是高斯核函數(shù),核函數(shù)的參數(shù)設(shè)置為迭代次數(shù)為20.得到每種算法的最高識別率,實(shí)驗(yàn)結(jié)果如表4和5所示.

從表4和表5可見,在擴(kuò)展YaleB人臉庫上,本文提出的K-DPL算法相比DPL算法提高了0.3%,識別速度較DPL、P-DPL更有競爭力; 而在AR人臉庫上,K-DPL算法相比DPL提高了0.4%,識別速度介于DPL和P-DPL之間.綜合來看,本文提出的K-DPL算法能夠?qū)τ泄庹兆兓驼趽醯娜四樳M(jìn)行有效識別,且相比DPL算法具有更強(qiáng)的識別能力.

表4 在擴(kuò)展 YaleB 庫上的識別結(jié)果比較

表5 在 AR 庫上的識別結(jié)果比較

5 結(jié)論

本文比較了DPL算法與MFL、SRC、CRC、FDDL等算法的性能,并提出了一種改進(jìn)投影字典對學(xué)習(xí)算法K-DPL,將KPCA與DPL相結(jié)合,從而取得了比DPL算法更好的識別性能.并在ORL人臉庫、擴(kuò)展YaleB人臉庫、AR人臉庫上驗(yàn)證了K-DPL算法的優(yōu)越性.實(shí)驗(yàn)結(jié)果表明,K-DPL算法在樣本數(shù)據(jù)量較小的ORL人臉庫上的識別速度提高了約20倍,識別率也得到較好地提高; 而在對有光照變化和遮擋的人臉庫上,K-DPL相比DPL表現(xiàn)出更高的識別率,且具有更快的識別速度,對光照和遮擋具有較強(qiáng)的魯棒性.

參考文獻(xiàn)

1楊榮根,任明武,楊靜宇.基于稀疏表示的人臉識別方法.計(jì)算機(jī)科學(xué),2010,37(9): 267–269,278.

2鄧承志.圖像稀疏表示理論及其應(yīng)用研究[博士學(xué)位論文].長沙: 華中科技大學(xué),2008.

3Wright J,Yang AY,Ganesh A,et al.Robust face recognition via sparse representation.IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(2): 210 –227.[doi: 10.1109/TPAMI.2008.79]

4Zhang L,Yang M,Feng XC.Sparse representation or collaborative representation: Which helps face recognition?Proceedings of 2011 IEEE International Conference on Computer Vision (ICCV).Barcelona,Spain.2011.471–478.

5練秋生,石保順,陳書貞.字典學(xué)習(xí)模型、算法及其應(yīng)用研究進(jìn)展.自動化學(xué)報,2015,41(2): 240–260.

6Pham DS,Venkatesh S.Joint learning and dictionary construction for pattern recognition.Proceedings of 2008 IEEE Conference on Computer Vision and Pattern Recognition.Anchorage,AK,USA.2008.1–8.

7Dorr BJ.Large-scale dictionary construction for foreign language tutoring and interlingual machine translation.Machine Translation,1997,12(4): 271 –322.[doi: 10.1023/A:1007965530302]

8Aharon M,Elad M,Bruckstein A.rmK-SVD: An algorithm for designing overcomplete dictionaries for sparse representation.IEEE Transactions on Signal Processing,2006,54(11): 4311–4322.[doi: 10.1109/TSP.2006.881199]

9Yang M,Zhang L,Yang J,et al.Metaface learning for sparse representation based face recognition.Proceedings of the 17th International Conference on Image Processing (ICIP).Hong Kong,China.2010.1601–1604.

10Yang M,Zhang L,Feng XC,et al.Fisher discrimination dictionary learning for sparse representation.Proceedings of 2011 IEEE International Conference on Computer Vision(ICCV).Barcelona,Spain.2011.543–550.

11Turk M,Pentland A.Eigenfaces for recognition.Journal of Cognitive Neuroscience,1991,3(1): 71 –86.[doi: 10.1162/jocn.1991.3.1.71]

12Sch?lkopf B,Smola A J,Müller KR,et al.Kernel principal component analysis.Proceedings of the 7th International Conference on Artificial Neural Networks.Lausanne,Switzerland.1997.583–588.

13徐蓉,姜峰,姚鴻勛.流形學(xué)習(xí)概述.智能系統(tǒng)學(xué)報,2006,1(1): 44–51.

14Ding M,Fan GL.Multilayer joint gait-pose manifolds for human gait motion modeling.IEEE Transactions on Cybernetics,2015,45(11): 2413 –2424.[doi: 10.1109/TCYB.2014.2373393]

15Kruskal JB.Nonmetric multidimensional scaling: A numerical method.Psychometrika,1964,29(2): 115–129.[doi: 10.1007/BF02289694]

16Roweis ST,Saul LK.Nonlinear dimensionality reduction by locally linear embedding.Science,2000,290(5500):2323–2326.[doi: 10.1126/science.290.5500.2323]

17Tenenbaum JB,de Silva V,Langford JC.A global geometric framework for nonlinear dimensionality reduction.Science,2000,290(5500): 2319–2323.[doi: 10.1126/science.290.5500.2319]

18Belkin M,Niyogi P.Laplacian eigenmaps for dimensionality reduction and data representation.Neural Computation,2003,15(6): 1373–1396.[doi: 10.1162/0899766033217 80317]

19Gu SH,Zhang L,Zou WM,et al.Projective dictionary pair learning for pattern classification.Proceedings of the 27th International Conference on Neural Information Processing Systems.Montreal,Canada.2014.793–801.