BC-AW協(xié)同過濾推薦算法研究①

張志強,李 改

1(順德職業(yè)技術學院 電子與信息工程學院,順德 528300)

2(華中科技大學 計算機科學與技術學院,武漢 430074)

3(中山大學 信息科學與技術學院,廣州 510006)

當今社會,基于互聯(lián)網(wǎng)技術的電子商務不斷普及,大數(shù)據(jù)分析和大數(shù)據(jù)挖掘已成為迫切要解決的問題.推薦系統(tǒng)是指根據(jù)用戶的興趣特點和購買行為,向用戶推薦用戶感興趣的信息和商品的系統(tǒng).其中協(xié)同過濾推薦 (collaborative filtering recommendation)是推薦系統(tǒng)中應用最早和最為成功的技術之一,它一般采用最近鄰技術,利用用戶的歷史喜好信息計算用戶之間的距離,然后 利用目標用戶的最近鄰居用戶對商品評價的加權評價值來預測目標用戶對特定商品的喜好程度,系統(tǒng)從而根據(jù)這一喜好程度來對目標用戶進行推薦.協(xié)同過濾最大優(yōu) 點是對推薦對象沒有特殊的要求,能處理非結構化的復雜對象,如音樂、電影等媒體數(shù)據(jù)[1].其中的潛在因素模型 (latent factor models)的核心思想是: 通過分析歷史數(shù)據(jù)來預測事物的發(fā)展趨勢,矩陣分解算法(matrix factorization)是其中最為成功的算法之一[2].但隨著互聯(lián)網(wǎng)數(shù)據(jù)的不斷擴大,應用傳統(tǒng)的矩陣分解算法構造大數(shù)據(jù)潛在因素模型,算法性能會大大下降,難以實現(xiàn)有效的協(xié)同過濾,其關鍵問題體現(xiàn)在數(shù)據(jù)稀疏性和算法可擴展性的改進上.

針對上述問題,國內(nèi)外學者專家們提出了一些改進想法: Pilaszy I最先提出基于ALS的協(xié)同過濾算法,相對傳統(tǒng)算法而言,能有效提高過濾質(zhì)量和推薦速度,但該算法只考慮用戶的相似性[3]; 李改等對前者進行改進,提出了ALS-WR 協(xié)同過濾算法,該算法考濾到可擴展性方面,但需要專門設計迭代式算法[4]; 王輝等把用戶聚類思想引入到協(xié)同過濾算法中,改進了傳統(tǒng)算法的數(shù)據(jù)稀疏性和可擴展性,但精確度較低[5].

本文提出一種基于BC-AW的協(xié)同過濾推薦算法,在傳統(tǒng)算法的基礎上,引入聯(lián)合聚類BC(BlockClust)和正則化迭代最小二乘法(Alternating least squares with Weighted regularization,AW).首先分解原始評分矩陣的用戶項目雙維度,然后使用聯(lián)合聚類計算出多個同類評分塊的子矩陣,最后使用正則化迭代最小二乘法預測各個子矩陣的未知評分,從而計算出推薦結果.使用聯(lián)合聚類所求得的子矩陣遠比初此矩陣規(guī)模小,可以大大減少過濾推薦的計算量.通過與BaseMF算法、RSTE算法、TidaTrust算法、MoleTrust算法進行對比實驗,分析結果表明,本文算法可以有效緩解傳統(tǒng)算法并行化、可擴展性差的問題.

1 AW 算法

設定矩陣代表個用戶、個對象的評分矩陣、矩陣代表用戶特征矩陣、矩陣代表推薦對象特征矩陣代表中的某個元素,代表的第i行代表的第列代表的轉(zhuǎn)置代表的逆.傳算法一般使用SVD算法來分解[6],但本文算法是通過計算低秩矩陣來逼近,使得(其中代表的特征數(shù)),一般狀態(tài)下代表的秩

Step1: 我們通過最小化Frobenius的損失函數(shù)來算出一個低秩矩陣,令的得盡量接近,如公式(1)所示:

上述公式(1)中為低秩逼近中一般平方誤差項.

Step 2: 求解的最優(yōu)化問題于是改寫公式(1)如下:

上述式(2)會產(chǎn)生過于擬合的問題,因此需要通過正則化項來解決這個問題,則改寫如下:

Step3: 對上面公式 (3),設定不變,對求導求解如公式 (4)所示:

公式(4)中,為用戶所評過影片的向量矩陣,由評分組組成,為用戶i所評過影片的特征矩陣,由特征向量組成,為用戶i所評過的影片數(shù),階的單位矩陣.

Step4: 上述對公式 (4)中,設定不變,可以通過公式(5)求解

上述公式(5)中為用戶i所評過影片的評分所形成的向量,為用戶i評過影片的特征矩陣,它由用戶群中的特征向量組成,為用戶i評過影片的用戶數(shù)量.

2 BC 算法

BC算法能夠?qū)⒂枚鄠€較小且高相似度的評分矩陣來替代原始數(shù)據(jù)[7].通過掃描該矩陣中的評分,使用聚類方法計算行和列,計算一次后,重新評估每個子矩陣中用戶、項目的概率,如此類推,直到產(chǎn)生收斂為止[8].然后將評分匹配到最大概率的子矩陣中.其算法思想如下:

首先掃描評分矩陣,通過計算各評分的所屬概率來判斷該評分是否屬于某個子矩陣,其參數(shù)包括: 用戶—項目屬于某子矩陣的概率該評分值屬于某子矩陣中的概率其算法公式如下(其中

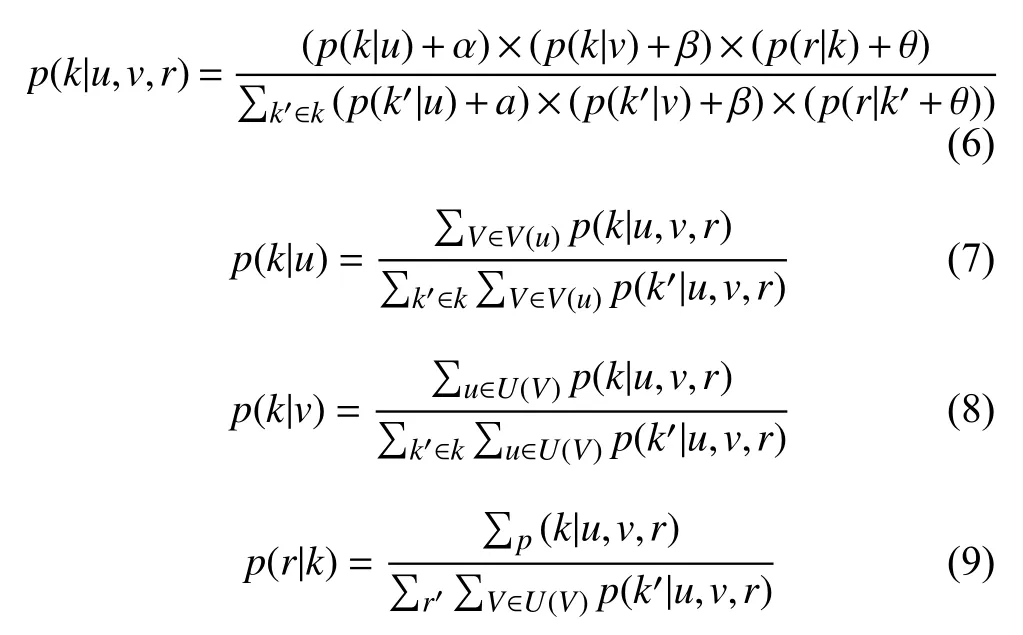
以上公式中,表示當前用戶,表示當前項目,表示評分值表示1到5的整數(shù),表示當前聚類表示當前累加聚類表示對評了分的所有用戶集合,表示已評過分的所有項目集合.BC算法把原矩陣分為個具有高密度、高相似度的子矩因此,該算法具有一定的降維作用[9].

3 BC-AW 算法

以下通過聯(lián)合聚類和AW協(xié)同過濾兩階段來對評分矩陣的未知項進行預測.

1) 聯(lián)合聚類

輸入: 子矩陣個數(shù),用戶—項目評分矩陣.

輸出: 子矩陣數(shù).

Step1:表示用戶量,表示項目數(shù)表示評分屬于聚類的概率,分別初始化使得

Step2: 應用公式(7)計算用戶屬于聚類的概率應用公式(8)計算用戶屬于聚類的概率應用公式(9)算出分值概率應用公式(6)算出

Step3: 最后選擇概率的最大值作為該評分的子矩陣.

Step4: 跳回步驟 2,直到出現(xiàn)收斂,結束循環(huán).

2) AW 協(xié)同過濾

首先用偏差小于等于的高斯隨機數(shù)初始化矩陣,接著分別用公式(4)和公式(5)更新和,重復進行多次迭代,直到得出的RMSE值出現(xiàn)收斂為止,結束迭代.

輸出: 用戶評分矩陣,特征個數(shù).

輸出:的逼近矩陣.

Step1: 用偏差小于等于0.01的高斯隨機數(shù)初始化;

Step2: 分別用公式(4)和公式(5)更新和;

Step3: 重復迭代公式 (4)、公式 (5),判斷得出的RMSE值是否收斂,如果是,則迭代結束;

Step4: 令返回矩陣

下面我們分析該算法的時間復雜度: 設為在矩陣里的評分點個數(shù),一般情況下,矩陣稀疏).為特征個數(shù),為該算法的迭代數(shù); 設為用戶數(shù); 設為對象推薦數(shù).變量每次更新的時間為變量每次更新的時間為如此類推,在迭代次后的時間則為由此可見,在以及恒定的情況下,)取決于也就是說,算法的總時間復雜度與成正比,可證該算法具有一定的可擴展性.在 AW 協(xié)同過濾中,Step 2 是最關鍵的步驟,在這個步聚里,每次應用公式(4)和公式(5)只能更新和中 的一行值,效率較低.因此可以先將和分解為個列相等的子矩陣,然后,應用公式(4)和公式(5)對每個子矩陣并行更新,這樣可以大大提高運算效率.

綜上所述,本文基于矩陣分解的BC-AW協(xié)同過濾推薦算法改進傳統(tǒng)算法的串行運算方式,實現(xiàn)并行運算,可以有效地解決傳統(tǒng)算法中存在的可擴展性差問題.

4 實驗分析

4.1 數(shù)據(jù)準備

本實驗目的是通過分析比較本文算法和傳統(tǒng)算法的性能,硬件方面選用基于云計算的分布式硬件實驗平臺,該平臺由20臺電腦組成20個運算節(jié)點,每個節(jié)點配有 4.0 Hz 的 Intel處理器和 32 G 的內(nèi)存,Linux 操作系統(tǒng).實驗數(shù)據(jù)來自美國Minnesota大學GroupLens項目組的MovieLens數(shù)據(jù)集.MovieLens數(shù)據(jù)集是GroupLens項目組開發(fā)的一個互聯(lián)網(wǎng)研究型推薦系統(tǒng)數(shù)據(jù)集.MovieLens數(shù)據(jù)集中含有943個用戶對1682部電影的100 000條評分數(shù)據(jù),平均每個用戶評分的電影大于等于20部[10].

4.2 評價指標

本次實驗采用均方根誤差RMSE和評分覆蓋率(Rating Coverage)作為算法推薦質(zhì)量的評價指標.

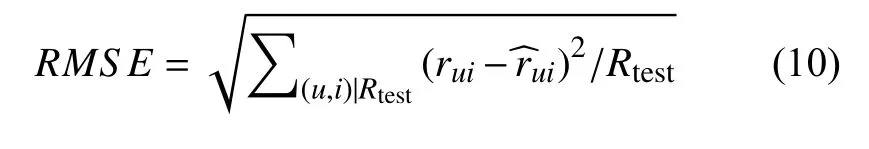
其中代表用戶的實際評分代表用戶對影片的預測評分,代表影片的評分數(shù).RMSE的值越小表示算法的精度越高.Rating Coverage 是指在測試集中,推薦系統(tǒng)可預測的評分數(shù)量占總評分的百分比[11].

4.3 實驗結果及分析

本文算法分別與BaseMF (基于矩陣分解算法)[12];RSTE (概率矩陣分解算法)[13]; TidaTrust (基于 TidaTrust模型推薦算法)[14]; MoleTrust (基于 MoleTrust模型推薦算法)[15]這4種推薦方法通過分析RMSE和的結果值進行分析比較.實驗開始,首先隨機選取兩組訓練集GROUP1和GROUP2: GROUP1為80%的Epinions數(shù)據(jù)集,GROUP1為90%的Epinions數(shù)據(jù)集.然后分別把本文算法、BaseMF 算法、RSTE算法、TidaTrust算法、MoleTrust算法所建立的模型應用到訓練集上進行學習,指定為潛在維度為實驗基礎反復實驗5次,求平均值作為最終實驗結果.圖1為這5種算法得出的RMSE值比較圖.

圖1 5 種算法的 RMSE 值比較圖

從上圖可以看出,針對RMSE值,當訓練集為80%時,本文算法比BaseMF算法降低了22%,比RSTE算法降低了11%,比TidaTrust算法降低了8%,比 MoleTrust 算法降低了 7%; 當訓練集為 90%,本文算法比BaseMF算法降低了21%,比RSTE算法降低了 10%,比 TidaTrust算法降低了 7%,比 MoleTrust算法降低了7%; 由此可知,本文算法的誤差值明顯低于傳統(tǒng)的4種推薦算法.

圖2(a)、圖2(b)分別表示本文算法在GROUP1、GROUP2這兩組訓練集中,RMSE在不同值下的變化情況.值越大,RMSE值越小,證明推薦精度越高.當時,RMSE減小的幅度最大,迭代時間的增幅最小; 當時,RMSE的變化幅度趨于 0.從而得出當時,算法的推薦性能最佳.

圖2 RMSE 隨參數(shù)的變化曲線

下面分析5種算法的我們知道直接影響用戶對影片的可選擇范圍越高,用戶對影片的可選擇范圍越廣,從而用戶滿意度越高.采用GROUP1數(shù)據(jù)集(即80%的訓練集),實驗結果如表1所示.

表1 5 種算法的 COVR

分析表1可以看出,當訓練集為80%時,本文算法的比BaseMF算法提高了68.52%,比RSTE算法提高了38.09%,比TidaTrust算法提高了4.84%,比 MoleTrust算法提高了 6.58%.由此可見,本文算法比傳統(tǒng)4種算法具有更廣的覆蓋范圍.

4 結論與展望

本文針對現(xiàn)有協(xié)同過濾算法中普遍存在的數(shù)據(jù)稀疏、可擴展性低這兩個核心問題,提出BC-AW(基于聯(lián)合聚類和迭代最小二乘法)兩階段協(xié)同過濾算法.首先由該算法通過對原評分矩陣進行用戶—項目雙維度聯(lián)合聚類后得到的若干個子矩陣(這些子矩陣均為模式相同的評分塊),其規(guī)模比原矩陣小得多,因此可以有效減少預測工作量; 再者,采用正則化迭代最小二乘法預測子矩陣的未知評分可以優(yōu)化推薦效率.該算法在模擬大數(shù)據(jù)實驗中(美國Minnesota大學GroupLens項目組的MovieLens數(shù)據(jù)集),通過與幾個經(jīng)典的協(xié)同過濾算法(BaseMF算法、RSTE算法、TidaTrust、MoleTrust算法)作比較.實驗結果表明,本文算法能有效改進推薦系統(tǒng)的稀疏性、可擴展性問題,系統(tǒng)預測評分與用戶實際評分接近,并能為用戶提供良好的使用體驗.

參考文獻

1Shuo LX,Chai BF,Zhang XD.Collaborative filtering algorithm based on improved nearest neighbors.Computer Engineering and Applications,2015,51(5): 137–141.

2Zhang HJ.The research and application of distributed matrix factorization algorithm in recommend system.Bulletin of Science and Technology,2013,29(12): 151–153.

3Wang QM,Miao Y,He M,et al.Parallelized research on collaborative filtering algorithm based on matrix factorization.Computer Technology and Development,2015,25(2): 55–59.

4Zhu X,Song AB,Dong F,et al.A collaborative filtering recommendation mechanism for cloud computing.Journal of Computer Research and Development,2014,51(10):2255–2269.

5Bi XR.Collaboration filtering recommendation algorithm of sub-similarity integration between items.Computer Systems& Applications,2015,24(1): 147–150.

6Wang L,Fu XF,Wang XM.Hybrid dynamic collaborative filtering algorithm based on big data sets.Journal of Guangdong University of Technology,2014,31(3): 44–48.

7Chen W,Shi QL.An adaptive algorithm for collaborative filtering recommendation.Journal of Xianyang Normal University,2014,29(6): 47–49.

8Li G,Li L.One-class collaborative filtering based on matrix factorization.Application Research of Computers,2012,29(5): 1662–1665.

9Ke LW,Wang J.Collaborative filtering recommendation based on user feature transfer.Computer Engineering,2015,41(1): 37–43.

10Yi ZA,Mu CM.Collaborative filtering algorithm based on subtractive clustering and genetic fuzzy.Computer & Digital Engineering,2014,42(8): 1363–1367.

11Xu W,Duan F.Combining clustering and collaborative filtering for implicit recommender system.Computer Engineering and Design,2014,35(12): 4181–4185.

12Liu L.A collaborative filtering recommender algorithm based on iterative kernel method.Information Technology &Informatization,2014,(12): 76–81.

13Zha J,Li ZB,Xu GQ.An optimised collaborative filtering algorithm based on combined similarity.Computer Applications and Software,2014,31(12): 323–328.

14Wu HC,Wang XJ,Cheng Y,et al.Advanced recommendation based on collaborative filtering and partition clustering.Journal of Computer Research and Development,2011,48(S3): 205–212.

15Luo Q,Miao XJ,Wei Q.Further research on collaborative filtering algorithm for sparse data.Computer Science,2014,41(6): 264–268.