基于通行異常行為的高速公路車輛信用度評價模型與算法研究

陳爾希，曾獻輝，胡征

（1.東華大學 信息科學技術學院，上海 201620；2.數字化紡織服裝技術教育部工程研究中心，上海 201620）

0 引言

隨著高速公路聯網規模的不斷擴大，行車距離越來越遠，對通過路網的車輛（尤其貨車等重載車輛）單次收費金額也越來越大，隨之而來的是利用各種作弊手段[1-6]逃費的車輛數的增加，因此逃費稽查越來越受到高速公路稽查部門的重視。目前，稽查部門主要以人工審核的方式綜合分析高速公路收費后臺數據，從而查獲逃費車輛。這種工作模式效率極為低下，漏判、誤判重要逃費線索數據時有發生。為了充分挖掘通行數據中的信息價值，提高稽查部門的工作效率，高速公路管理部門迫切需要利用新技術來提升逃費稽查水平。

目前，國際上有關防逃費方面的研究有：Delbosc等[7]采用聚類分析法對逃費行為展開研究；Guarda等[8]、Troncoso等[9]針對高頻的公交逃費問題，通過負二項式回歸模型發現了導致逃費率增加的幾個關鍵因素，并提出規避逃費問題的五種方法；Jankowski[10]利用博弈論對逃費的動機進行了分析，并指出不同博弈參與者的利益動機，同時從博弈角度給出了一些防逃費建議。在國內，關于防逃費的研究主要有：刁洪祥等[11-14]，劉勇等[15]采用聚類分析法、決策樹和神經網絡算法對聯網收費數據進行建模和分析逃費車輛，并提出了部分防逃費措施，但其研究基本停留在理論階段，尚未應用到逃費稽查中；趙彥等[16]采用聚類分析、判別分析和邏輯回歸分析相結合的方法，構建了通行卡逃費行為預測模型，但該模型對非超時逃費行為的識別能力不足；張曉航[17]提出使用數據挖掘工具WEAK實現對車牌不符、變檔等部分逃費行為的稽查。從實際應用來看，這些方法存在數據收集困難、準確性較低、實際應用難度高等問題。

隨著高速公路大數據系統的形成，如何直接從車輛通行數據中挖掘出逃費車輛，對逃費稽查的實際應用具有重要意義。為此，筆者將基于浙江省某高速公路近三年的通行歷史數據，結合稽查部門的逃費車輛歷史記錄，分析逃費行為發生時可能出現的各種異常通行行為，提出用于評判車輛逃費可疑程度的車輛通行信用度評價指標，給出計算該指標的多屬性效用模型，并利用BP神經網絡算法對該模型進行改進，最后對結果的適用性和準確度加以驗證。

1 車輛通行異常行為分析

高速公路通行費計算方法是根據車輛在高速公路的出入信息和路徑信息，查找對應車型在所經過路段的基本費額，考慮車輛重量等因素，分別乘以對應的通行里程，最后匯總相加得出該車通行的總費額。據此，車輛可能通過縮短里程或改變車型兩種方式實現通行費的偷逃。通過對稽查過程調研和已有偷逃車輛通行數據的分析，現歸納出11種典型的車輛通行異常行為，如表1所示。

表1 車輛逃費時可能出現的異常行為

以上11種異常行為對判斷車輛是否存在逃費行為提供了非常有價值的依據，異常出現次數越多，逃費的可能性就越大。基于此，本文將逃費稽查看作一個考慮多個評價屬性的決策性問題，構建以11種異常出現次數為評價屬性的車輛信用度評價模型。利用該模型計算得到每輛車的信用度值，并據此判斷車輛逃費可疑度的大小，即信用度值越小，則出現逃費行為的可能性就越大。在實際應用時，可考慮將信用值較小的車輛提供給稽查部門，從而提升人工稽查的效率和準確度。

2 基于多屬性效用模型的車輛信用度評價

2.1 車輛信用度

為了有效地甄別最有可能偷逃通行費的車輛，本文提出對每一輛車建立信用度的概念。該信用度僅用于對車輛在高速公路通行中出現各種異常情況的度量。信用度的取值范圍為0～100分，其中100分為信用度滿分，表示基本未出現過異常；0分是最差值，表示所有類別的異常出現次數都最多。車輛初始信用度值均為100分，根據出現異常的類別及次數，該值將逐步降低。

2.2 車輛信用度計算

以車輛信用度作為衡量車輛逃費可疑程度的量化指標，其計算可以看作是一個基于車輛異常行為出現次數的多屬性效用模型的決策問題，即考慮車輛的11種異常行為出現次數及其重要程度，通過某種計算模型，得到定量的綜合評估值。本文采用基于加權平均的多屬性效用模型進行車輛信用度計算，具體采用扣分的方式進行。首先，計算各類異常下每輛車的扣分情況，異常越多，扣分越多，最多扣100分；然后，將所有異常類型的扣分進行加權平均，得到對應車輛的總扣分；最后，用100分減去總扣分，即得到車輛的最終信用度值，計算方法為：

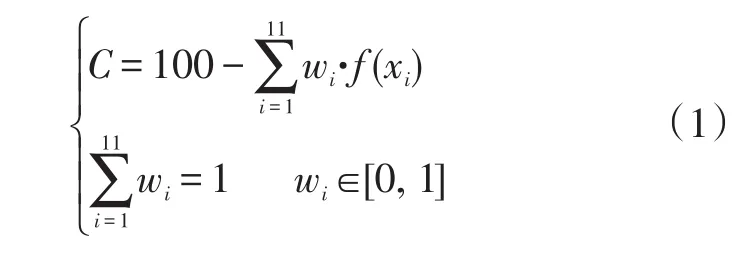
式（1）中：C為車輛信用度（分）；wi為第i類異常的權重值；xi為第i類異常出現的次數（次）；f(xi)為第i類異常出現次數的效用函數。

2.3 信用度評價模型構建

從式（1）可以看出，信用度評價模型的構建可分為兩個步驟：

（1）確定每類異常的權值；

（2）確定每類異常出現次數的效用函數。

目前已有很多理論和方法用于確定權值，比如主觀賦值法、客觀賦值法和機器學習法等。本文通過對稽查人員的問卷調查、統計分析和多次試驗，得到相應的權值。鑒于各類異常出現的次數雖然差別很大，但其效用函數基本相同，同時由于信用度的定義區間為[0,100]，而異常次數的取值可能會超過100，故需要對異常出現次數進行預處理，將數據歸一化到0～100范圍內，否則可能出現信用度值為負的情況，這是沒有意義的。

本文效用函數的構建思路是：首先找出各類異常的平均出現次數，然后估計出最大可能出現次數，最后利用歸一化處理將效用值統一到0～100之間，具體按下式計算：

式（2）中：Xiavg為第i類異常的平均次數（次）；Ximax為第i類異常的最大次數（次）；f(xi)與xi的意義同式（1）。

2.4 模型準確率驗證

為了驗證模型的適用性和有效性，本文基于浙江省某高速公路公司2015—2017年的通行數據，分析得到約3×107輛車的通行異常行為數據，接著利用前文給出的方法計算得出所有車輛的信用度值。部分車輛通行異常行為數據與信用度值如表2所示。表中的異常行為次數是根據高速公路車輛通行流水數據分析所得，比如車輛進出站車牌不一致，根據收費系統中車輛進出站的車牌，對比其相似度，相似度值大于或等于某個設定值，則認為車牌是一致的，否則便不一致，對應類型的異常次數加1。

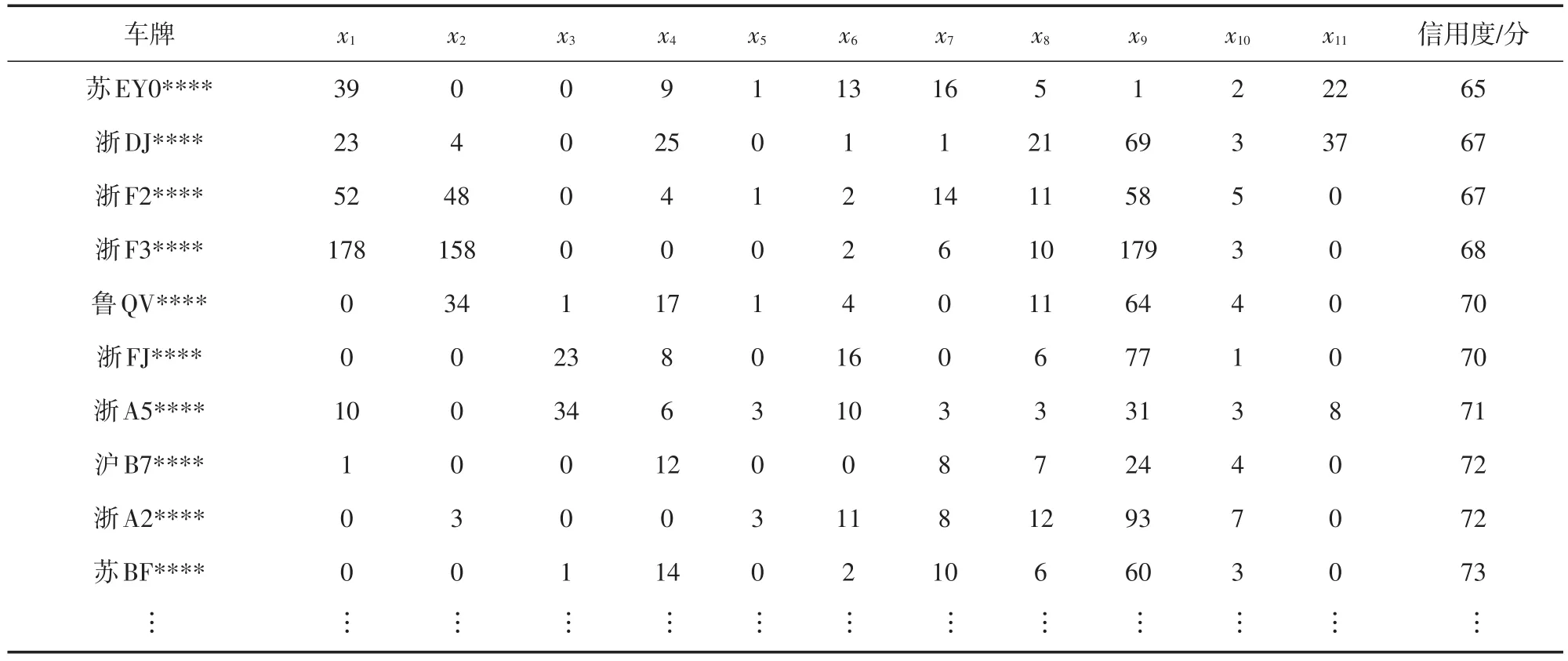
表2 車輛的通行異常行為數據與信用度值

面對海量的車輛數據，不可能對每輛信用度值較低的車輛進行稽查。為了盡快發現有問題的車輛，將信用度最低的200輛車的信息提供給稽查部門進行稽查，最終發現實際存在問題的車輛有30輛，其中19輛車曾被稽查過（新發現的問題車輛為11輛），另外還有35輛車無確鑿證據，其余為正常車輛，模型正確率約為33%。可見，所建模型雖然準確率不高，但對逃費稽查工作還是有一定幫助的，可在一定程度上減少人工稽查的工作量，起到輔助稽查的作用。這同時說明本文提出的方法是正確的，也表明車輛通行異常數據與逃費行為之間的確存在一定的對應關系。

分析發現，多屬性效用模型正確率不高的原因在于：

（1）線性模型過于簡單，無法準確地表示異常行為次數與車輛信用度值之間的關系；

（2）權重值分配不合理，權值的確定存在很大的主觀性；

（3）線性效用函數可能不夠準確。

為了提高信用度計算的準確度，下面在線性模型的基礎上利用BP神經網絡的自學習功能對模型進行改進。

3 基于BP神經網絡的改進車輛信用度評價模型

BP神經網絡是使用最廣泛的一種神經網絡模型之一，它利用梯度下降算法，使權值沿著誤差函數的負梯度方向改變，以期使網絡的實際輸出與期望輸出的均方差最小化。由于BP神經網絡算法能夠自主學習出一組具有代表性的權值和閾值，且具有良好的非線性逼近能力，故選用BP神經網絡算法對多屬性效用模型進行改進。BP神經網絡的設計主要包括網絡層數（主要指隱含層層數）、各層節點數、傳遞函數、權值等，具體過程如下。

3.1 神經網絡結構的確定

BP神經網絡通常分輸入層、輸出層和隱含層，其中隱含層可以為一層或多層。本文選擇最典型的三層BP神經網絡，即隱含層為一層。BP神經網絡的傳遞函數是Sigmoid函數。

輸入層的節點數應等于輸入向量的分量數目。本文所建信用度模型的輸入量為車輛的11種異常行為特征，故輸入層節點數為11。輸出層節點則由信用度決定，故確定輸出層節點數為1。

雖然增加隱含層層數可以降低網絡誤差，提高精度，但也會使網絡復雜化，延長網絡訓練時間，甚至出現“過擬合”的傾向，故隱含層節點數的確定對于模型可用性非常關鍵。根據專家和學者的經驗[18]，隱含層節點數Lh可按下式計算：

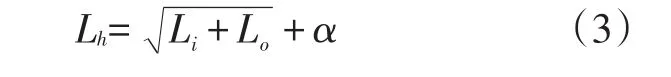
式（3）中：Li和Lo分別為神經網絡輸入層和輸出層的節點數（個）；α為0～10之間的常數。

現取Li=11，Lo=1，經過多次仿真實驗發現，當α=3，即隱含層節點數為7時，模型的準確率最高。

綜合以上，本文BP神經網絡結構確定為：輸入層節點數為11，中間層節點數為7，輸出層節點數為1，其拓撲結構如圖1所示。

圖1 用于計算車輛信用度的BP神經網絡拓撲結構

3.2 初始權值的確定

一般情況下，初始權值要足夠小才有利于模型的訓練。在神經網絡中，如果簡單地將權值矩陣初始化為零矩陣，將會導致隱含層的每個單元相等。為了讓學習更有效率，一般將該矩陣初始化在區間[-ε,ε]內。初始權值按下式計算：

式（4）中：ε是取值為0～1的數；Θ為1×12的權值矩陣，且矩陣中的每個單元取值均在區間[-ε,ε]內；Li和Lo意義同前。

3.3 學習速率的確定

學習速率決定每次訓練所產生權值的變化量，過大的學習速率可能導致系統不穩定；否則，又會導致較長的訓練時間。為保證系統的穩定性，學習速率通常取值偏小，在0.01～0.7之間，本文取0.01。

4 預測結果分析

為了驗證經BP神經網絡算法改進后的多屬性效用模型的準確率是否有所提升，本文基于多屬性效用模型計算出的信用度值，根據人工評價和以往稽查數據對部分樣本輸出數據加以調整，作為BP神經網絡的輸入數據進行網絡學習。將樣本數據的80%作為訓練集，10%作為驗證集，剩余的10%作為測試集，使用Matlab神經網絡工具箱完成模型的建立與仿真。為了找出所訓練多個模型中的效果最佳者，使用各個模型對驗證集數據進行預測，并記錄模型的準確率。接著，采用效果最佳模型所對應的參數來調整模型參數。待模型訓練完成后，利用其測試樣本中的車輛進行信用度預測。部分測試數據的預測輸出和預測誤差如圖2和圖3所示。

圖2 模型預測輸出與期望輸出圖

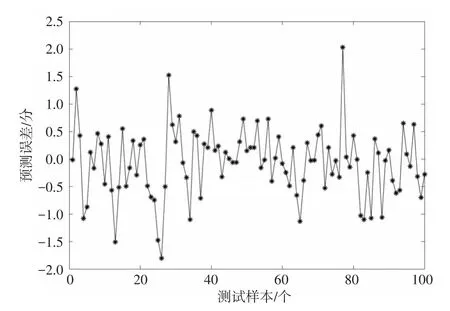
圖3 模型信用度預測誤差曲線

選取全量數據進行測試，仿真結果顯示模型的誤差約為3，即該模型預測所得車輛信用度值誤差為3分左右，顯然該精度能夠滿足應用要求。

BP神經網絡學習完成后，本文對近3×107條車輛通行異常行為數據重新進行計算，得到每輛車新的信用度值。然后，將信用度最低的200輛車提供給稽查部門進行稽查，最終發現實際存在問題的車輛有91輛，其中32輛車曾經已被稽查過（新發現的問題車輛為59輛），另外還有43輛車無確鑿證據，其余為正常車輛，整體正確率為67%左右，取得了令人滿意的效果。

與多屬性效用模型相比，BP神經網絡模型的稽查正確率從33%提升至67%，而且省去了復雜的權重確定過程，另外有效的學習能力使其具有較好的適應性，對提升高速公路稽查水平具有很大幫助。

5 結語

本文提出了以車輛信用度作為衡量逃費可疑度的量化指標，給出了基于BP神經網絡模型的車輛信用度計算方法。該研究成果已實際應用于浙江省某高速公路公司，取得了較好的效果。稽查部門根據模型給出的信用度值，實現了對逃費可疑車輛的精準稽查，降低了工作強度。不過，本文提出的模型對于沒有在收費系統中留下逃費痕跡的逃費行為不具備稽查能力，在下一步研究中，將提升算法的自學習能力，降低算法對樣本的依賴程度，例如可考慮深度學習等算法；采用模糊數學模型實現對車輛信用度的評價，有效降低對異常行為次數值的依賴，使模型的準確率更高。

參考文獻

[1]張友權.淺談高速公路車輛逃費的主要方式及其應對策略[J].北方交通，2011（8）：66-68.

[2]楊偉明.高速公路聯網收費逃費作弊情況分析及其對策[J].中國高新技術企業，2007（15）：144-147.

[3]楊淑芹.聯網收費防止利用通行卡逃漏費的途徑和有效措施[J].交通世界（運輸·車輛），2005（11）：51-53.

[4]潘亮華.高速公路逃費手段及防治辦法[J].中國交通信息化，2011（2）：99-100.

[5]韓慧英.高速公路逃費探源[J].安全與健康，2005（22）：10.

[6]唐州生.高速公路車輛偷逃通行費的原因及應對措施[J].西部交通科技，2011（3）：70-73.

[7]DELBOSC A,CURRIE G.Cluster Analysis of Fare Evasion Behaviours in Melbourne,Australia[J].Transport Policy,2016,50:29-36.

[8]GUARDA P,GALILEA P,PAGET-SEEKINGS L,et al.What is Behind Fare Evasion in Urban Bus Systems?An Econometric Approach[J].Transportation Research Part A:Policy&Practice,2016,84:55-71.

[9]TRONCOSO R,GRANGEE L D.Fare Evasion in Public Transport A:Time Series Approach[J].Transportation Re?search Part A:Policy&Practice,2017,100:311-318.

[10]JANKOWSKI W B.Fare Evasion and Noncompliance:A Game Theoretical Approach[J].International Journal of Transport Economics,1991,18(3):275-287.

[11]刁洪祥.ETC系統客戶數據異常檢測方法的研究[D].長沙：長沙理工大學，2004.

[12]刁洪祥.基于模糊C-均值聚類的ETC系統客戶的逃費分析研究[J].企業技術開發，2005（10）：8-10.

[13]刁洪祥.基于穩定遺傳神經網絡的ETC系統客戶逃費分析[J].電腦與信息技術，2006（4）：16-19.

[14]刁洪祥，劉偉銘.基于BP神經網絡的ETC系統客戶的流失分析研究[J].企業技術開發，2006（9）：34-36.

[15]劉勇，刁洪祥，劉偉銘.基于改進的模糊決策樹ETC系統客戶欺詐分析研究[J].交通與計算機，2006（2）：1-4.

[16]趙彥，吳淑玲，林志恒，等.高速公路通行卡逃費行為預測模型研究[J].中國科技論文，2015,10（19）：2245-2251.

[17]張曉航.高速公路聯網收費稽查管理應用研究[D].西安：長安大學,2010.

[18]王小川.MATLAB神經網絡43個案例分析[M].北京：北京航空航天大學出版社，2013.