基于聚類和改進共生演算法的云任務調度策略

李昆侖，關立偉，郭昌隆

(河北大學 電子信息工程學院，河北 保定 071000)

0 引言

云計算是近幾年發展起來的一種按需共享信息服務模式，是未來網絡服務的重要形式[1]。云計算系統將不同物理位置上的資源整合為一個邏輯整體，為用戶提供一體化應用服務，因此，云環境中的任務調度與資源分配關系著整個云平臺的使用效率，其模型的優劣直接關系到云計算系統是否能夠提供有效的、可靠的服務，任務調度是云計算的關鍵技術之一[2-4]。

在云環境中，以遺傳算法(Genetic Algorithm, GA)和粒子群優化(Particle Swarm Optimization, PSO)算法等為代表的群體優化算法被廣泛地應用于解決調度問題并取得了可觀的效果[5-8]。這些算法往往單一考慮調度代價，云計算的目標是按需提供服務，單純的計算時間、通信消耗或負載均衡無法滿足現實需求。因此，基于服務質量(Quality of Service, QoS)的調度算法被相繼提出，主要分為基于成本的QoS和基于用戶滿意度的QoS。基于成本的QoS綜合考慮執行時間、負載均衡、資源利用率等，如文獻[9]提出一種基于成本的QoS驅動算法，算法不僅考慮了最大完工時間和負載均衡，還考慮了對任務進行分配時的時間和通信損耗，減小了調度代價。文獻[10]提出一種多QoS約束的調度算法，以執行時間和資源利用率作為約束條件，并在動態環境中依據用戶預算和截止期限來完成對任務的調度，保證了較高的資源利用率和較少的調度時間。基于用戶滿意度的QoS指在用戶能在期望時間內完成任務的前提下，使用戶的綜合滿意值最高。王娟等[11]為了滿足不同用戶的QoS偏好，提出了一種具有偏好感知的粒子群算法，該算法為防止占有率較高的任務偏好掩蓋占有率低的任務，采用了按優先級分別調度任務，提升了用戶的QoS。而文獻[12]同樣將用戶按QoS進行分類并對類別按優先級來進行調度，與文獻[11]不同的是該算法設定了類間與類內的雙優先級，進一步提升了用戶的滿意度。

以上基于QoS的算法滿足了不同場景的調度需求，但進行調度的任務面向全體服務資源，存在選擇開銷和計算量較大的問題。現有研究表明，對資源進行聚類預處理是解決該問題的有效方式，如杜曉麗等[13]提出的有向無環圖(Direct Acyclic Graph, DAG)任務調度算法，陳志剛等[14]提出的資源多維性能聚類任務調度算法，以及李文娟等[15]和郭鳳羽等[16]采用的基于模糊聚類的云任務調度算法等。這些算法證明引入聚類操作可降低任務調度開銷，為本文提供了有益參考。因此，本文算法旨在解決以下問題：1)傳統調度算法未綜合考慮用戶滿意度與調度成本，沒有完全體現云計算廉價按需服務的宗旨；2)智能算法對資源的選擇開銷大，收斂速度慢。基于聚類的算法執行代價小，但尋求最優分配能力往往低于智能算法。故當處理的任務量增加，傳統算法不能平衡執行代價與尋優能力間關系。

針對上述問題，提出一種基于聚類和改進共生演(Symbiotic Organisms Search, SOS)算法的云任務調度策略。以提升云系統性能和云用戶滿意度為目標構造評價函數，進一步體現云計算廉價按需服務的宗旨。將任務與資源進行聚類處理，減小對資源的選擇開銷、提高收斂速度；依據改進的共生演算法進行細節處理，加強算法尋優能力。對比實驗表明，綜合聚類操作和共生演算法優點的調度策略擁有較快的收斂速度和較強的尋優能力，驗證了本文算法在基于批量模式的云任務調度問題上的有效性。

1 云計算任務調度模型

目前，Google提出的MapReduce編程模式[17]是目前云環境中應用最廣的編程模型，其基本執行過程如圖1所示。

圖1 Map/Reduce 云任務調度模型 Fig. 1 Map/Reduce cloud task scheduling model

Mapreduce共有6個過程，分為兩個階段：Map階段和Reduce階段。Map階段將一個較大任務通過Map/Reduce函數分成N個較小任務并分配給多個Worker并行執行，然后輸出中間文件保存在本地。Reduce階段將Map階段處理的結果進行分析和匯總并輸出最終結果。

依據上述模型，任務與資源可描述如下：

T={t1,t2,…,tn}表示待處理的任務集合，n=|T|代表子任務數，第i個任務刻畫為ti={tlength,tsource,tstorage}，其中tlength表示任務長度，tsource表示傳輸數據量，tstorage表示所需存儲空間。

R={r1,r2,…,rm}為云環境中的可用資源，m=|R|代表有效資源數。第j個資源rj(j∈[1,m])可以進一步刻畫為rj={rcomput,rbandwidth,rstorage}。其中：rcomput為資源的計算能力，rbandwidth為資源的傳輸能力，rstorage表示資源的存儲能力。

2 基于聚類和改進共生演的云任務調度策略

2014年，Cheng等[18]通過模仿自然界中不同生物間關系，提出一種新型優化算法——共生演(Symbiotic Organisms Search, SOS)算法。SOS算法最初用來解決復雜函數的優化問題，其易于實現且魯棒性強，已被相繼用來解決旅行商問題(Travelling Salesman Problem, TSP)、結構優化問題和控制問題等[19-22]。

2.1 標準共生演算法

SOS算法包含共生、共棲和寄生3個過程，描述如下。

共生過程：

Xinew=Xi+rand(0,1)*(Xbest-Mutual_Vector*BF1)

(1)

Xjnew=Xj+rand(0,1)*(Xbest-Mutual_Vector*BF2)

(2)

Mutual_Vector=(Xi+Xj)/2

(3)

其中：Xi為第i個個體，Xj是隨機與Xi相作用的個體。rand(0,1)是[0,1]間的隨機數，BF1和BF2取值為1或2。

共棲過程：

Xinew=Xi+rand(-1,1)*(Xbest-Xj)

(4)

其中：rand(-1,1)為[-1,1]隨機數，(Xbest-Xj)反映一種受益關系，由Xj提供信息提升Xi的存活率。

寄生過程：

Xinew=Xp

(5)

Xp為系統中個體通過隨機修改不同維數中的數值產生，能夠增加種群多樣性，防止陷入局部最優。

2.2 共生演算法的改進

文獻[23]采用式(6)對SOS算法進行離散化，并證明在解決云任務調度問題時，離散共生演算法(Discrete Symbiotic Organisms Search, DSOS)相比PSO等智能算法能夠得到更好的調度結果。本文以DSOS作為基本算法并對其進行以下改進，可進一步提高收斂速度和減小算法陷入局部最優的概率。

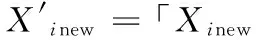
(6)

Xinew為更新個體，「?為ceil函數，mod為求余函數。

2.2.1 考慮潛在解的離散共生演算法

DSOS是一個更新與淘汰的過程，直接淘汰適應度低個體可能會損失潛在優秀解。如圖2，黑色標記代表已找到最優分配位置，灰色代表未找到最優分配，其中A1代表當前最優，A2、A3為相比較的個體。很明顯A2適應度大于A3，但若要實現全部最優分配，A2需要改變兩部分片段，A3只需改變一部分片段，所以在尋優速度上，A3很可能會大于A2。

圖2 三種個體基因比較 Fig. 2 Comparison of three individual genes

為克服上述缺陷，本文提出一種交叉方式，盡量減小優秀潛在解的損失，見式(7)：

(7)

其中:J(x)為判斷函數，接受更優個體，G(x1,x2)為在x1,x2間進行交叉變異的函數，隨機選取交叉點，為防止交叉后個體與當前最優相同，變異位在最優片段范圍選取，Xi為第i代適應度更高個體，Xzi為第i代暫時淘汰個體，Xbesti為第i代最優個體。

2.2.2 旋轉學習尋優操作

2.2.1節在一定程度上加強了算法的性能，但算法依然可能陷入局部最優。因此，為增強算法的勘探能力，補充種群多樣性，本文用旋轉學習機制(Rotation-Based Learning, RBL)更新個體。

旋轉角度決定RBL性能，角度固定，則學習范圍固定。DSOS前期探索能力強，后期弱，固定旋轉不適用SOS算法高效更新，因此，本文采用自適應角度旋轉：β=d·2*π/Iter，d取值1或-1，決定旋轉方向，Iter為迭代次數。該角度設定滿足算法前期大范圍搜索和后期小范圍搜索的情況。

如圖3所示，b和a對應搜索空間的上下限，C為[a,b]中點，以C為圓心，(a+b)/2為半徑作圓，設Z為N點坐標。

圖3 二維空間中的旋轉學習機制 Fig. 3 Rotational learning mechanism in two-dimensional space

將旋轉學習機制嵌入到算法的操作為：

1)選取個體Xi對其每一維度都進行旋轉學習，如下：

(8)

2)對M以旋轉角度β進行旋轉至P，點P在x軸上的投影Q為對應旋轉學習的結果，則：

(9)

推廣至高維情形，對應的旋轉數可表示為：

z*=(ai+bi)/2-(μj×cosβ-νj×sinβ)

(10)

3)采用式(11)對學習點進行離散化，選取優秀個體進入下代種群:

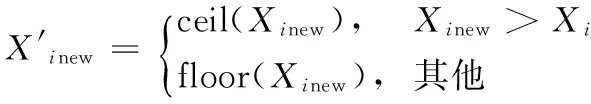
(11)

式(11)的離散方式更適合本文對β角的規定，實驗表明該離散方式比直接采用ceil、floor或mod函數更有效。

2.3 資源與任務的模糊聚類

2.3.1 經典模糊C均值算法

模糊C均值(Fuzzy C-Means, FCM)是Bezdek于1981年提出[24]，是基于目標函數聚類算法中較完善、應用較廣的一種算法。任務或資源間沒有確定的分界線，具有模糊特性，因此本文采用FCM對任務和資源進行模糊分類。FCM目標函數為：

(12)

其中：μij表示隸屬度，ci是模糊組i的聚類中心，dij=‖ci-xj‖為第i個中心與第j個數據間的歐氏距離，m是一個加權指數。

2.3.2 資源的重排序放置與任務的模糊聚類

任務調度結果主要受資源計算能力、通信帶寬和存儲能力的影響，因此許多學者主要從處理能力、通信能力和存儲能力三方面考慮資源的性能。本文參考文獻[14-15]，將資源模糊分為計算型資源、帶寬型資源和存儲型資源三類，并對其進行重排序放置，如圖4所示。

圖4 資源的聚類重排序 Fig. 4 Clustering and reordering for resources

操作過程如下。

1)用式(13)對任務與資源進行模糊量化：

(13)

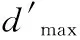
2)設置閾值t、迭代次數k和隸屬度矩陣U，將資源分為R1、R2、R33類，將任務分為T1、T2、T3類。

3)依據類別相似度對資源集合按性能由高到低進行排序，并再次設定閾值t′，使滿足‖tmi-tmc‖≤t′的任務i歸入到第m(m=1,2,3)類,剩余任務納入第4類，tmc為第m類聚類中心。

4)利用如下公式計算任務集需求度和資源綜合能力：

(14)

(15)

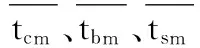
5)按式(16)對任務進行指導分配；

da=‖tcd-rp‖

(16)

2.3.3 聚類的效用分析

受積木原理的啟發，稱聚類效用為積木效用，即在有限空間內放置積木塊使積木高度最低。表1為初始化后相應資源擬分配到的任務，依據分配結果可將相對應任務量和資源的計算能力抽象為兩組積木塊組合，如圖5將任務抽象為計算量積木，積木的長度代表對資源計算能力的需求。將資源抽象為性能積木，積木長度為處理單位任務量的時間消耗。

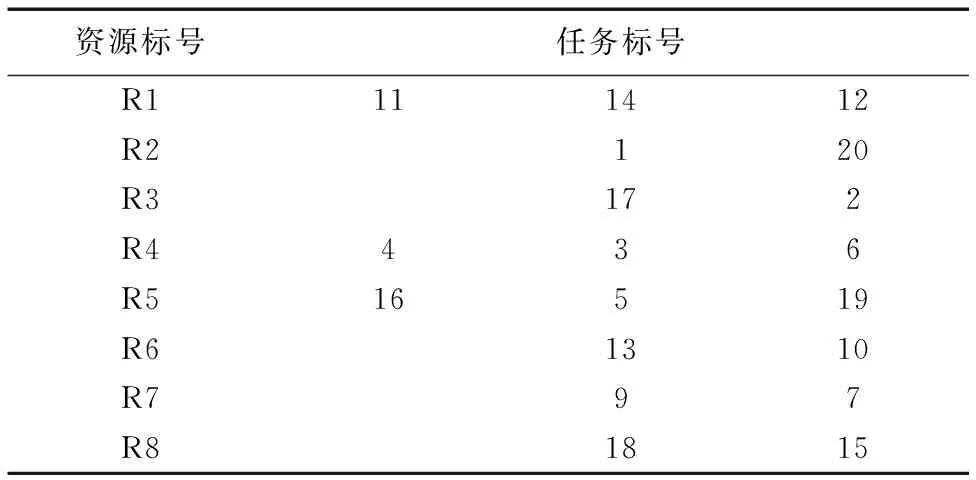
表1 資源所分配到的任務Tab. 1 Tasks assigned to resources

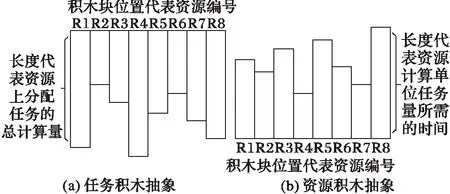
圖5 任務與資源的積木抽象 Fig. 5 Task and resource abstract model

理想的調度結果是使完工時間最短且負載均衡，即任務積木與資源積木的最優壘積，如圖6。

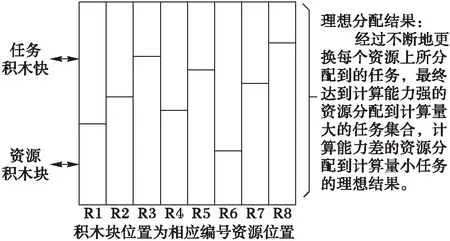
圖6 理想分配效果 Fig. 6 Ideal assignment results

未經任何處理的資源初始化后任務分配沒有任何規律，可看出得到由圖5到圖6的結果需要多次搜索且不一定能得到最優分配。針對該問題，本文采用聚類操作可在一定程度上改善算法性能。首先對資源進行聚類后按類間相似度和相鄰資源差異度重新排序放置，使得資源在虛擬空間中按標號有規律地放置，如圖7所示。

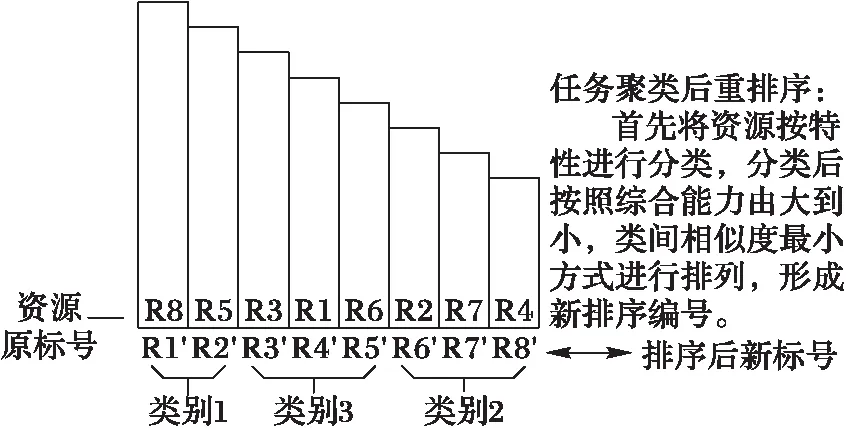
圖7 資源聚類后重排序放置 Fig. 7 Reordered placement after resource clustering

對任務進行聚類后，同一類別任務對資源需求具有相似性，進行調度時必然偏向選取排序后資源的相似位置，使任務進行分配具有一定的目的性。經過指導迭代后便可得到如圖8所示供需吻合的粗略結果。指導迭代是指通過計算任務集合對資源集合的需求來指導該類別任務在編碼中的位置，以吻合相對應資源類別的迭代。

與傳統算法不同，本文設定任務聚類集合為動態類集合，操作過程中同一類別任務依然可以選擇非與該類最相似的資源集合，即某類任務較多時，可將部分任務調度到其他類資源進行處理，可保證系統的負載均衡。聚類后開始執行調度算法，每次調度針對同一類別任務進行(其他類別任務作為約束信息)，因此稱本步操作為細節搜索階段。實驗證明本文方法更易得到與資源吻合的理想結果，如圖9所示。

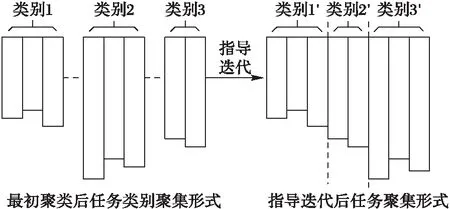
圖8 聚類及指導迭代后任務聚集形式 Fig. 8 Task aggregation form after clustering and guided iteration

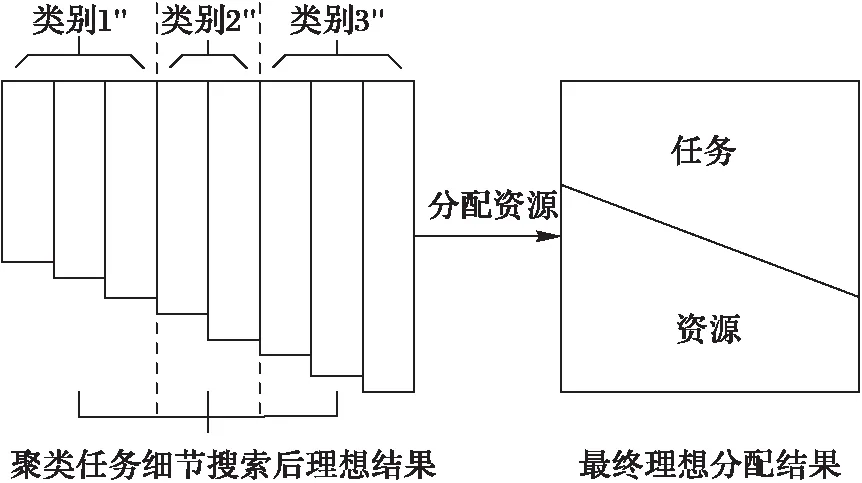
圖9 最終理想分配結果 Fig. 9 Final ideal assignment results

聚類后不易進入局部最優的原因：本文改進的共生演算法主體用式(1)～(5)進行種群更新并利用式(6)進行離散化。由于算法的貪婪選擇特性，算法后期種群中的個體具有極強的相似性，在空間隨機選取的進行共生的兩個個體可表示為Xi=Xs,Xj=Xs且Xbest=Xs,因此式(1)可描述如下：

Xinew=Xi+rand(0,1)*(Xbest-BF*(Xi+Xj)/2)=

Xs+rand(0,1)*(Xs-BF*(Xs+Xs)/2)=

Xs+rand(0,1)*(Xs-BF*Xs)

Xs-BF*Xs的取值為0或Xs，因此Xinew的取值范圍為：

max(Xinew)=Xs+0*(Xs-BF*Xs)或

max(Xinew)=Xs+rand(0,1)*0=Xs

同理得到：

min(Xnew)=Xs+1*(Xs-2*Xs)=Xs-Xs=0

Xinew=Xi+rand(-1,1)*(Xbest-Xj)=

Xs+rand(-1,1)*(Xs-Xs)=Xs=Xi

上式表明共棲過程后期可能起不到更新種群的作用，前兩步搜索不到的位置只能依靠寄生操作實現，但寄生操作不一定能夠得到有效更新，算法在后期搜索效率低下。

對資源和任務進行聚類后上述問題得到改善，算法后期任務雖只能搜索到小于當前標號的資源，但是聚類后的資源聚集在相似位置，相似任務目的性地搜索資源，使算法后期依然以更大概率搜索到全局最優。本文又將資源按照處理能力由高到低的順序排列如圖7，使得處理能力強的資源能夠被搜索到的概率更大，避免了處理能力強資源閑置的現象。因此，本文采取的聚類操可加強算法尋優能力。

2.4 編碼策略

傳統編碼形式多為資源-任務間接編碼形式，X={x1,x2,…,xN},其中N代表任務總數，xi代表第i個任務所分配的處理機標號。

本文采取聚類操作和指導迭代，每次進化操作均對同一類別個體進行，傳統編碼形式并不適應此操作，因此，本文提出一種可變資源-任務間接編碼形式，X={xi1,xi2,…,xin}∪ {xj1,xj2,…,xjm}∪{xz1,xz2,…,xzp},其中i、j、z代表類別標號，n、m、p為每個類別的任務數，n+m+p=N，N為總任務數。

∪位置為可交換節點，片段染色體位置可更改，片段染色體針對相應類別個體進行編碼產生。因此，依據指導迭代更新片段染色體位置，減小了對資源的選取范圍，對片段內個體進行更新，可加強算法的細節搜索能力。

2.5 評價模型

為體現云計算廉價按需提供服務的宗旨，本文提出一種綜合調度成本和用戶滿意度的驅動模型。

將同一物理平臺或應用服務于盡可能多的用戶，必須減小資源的空閑率，提高資源的整體使用率，從而使得成本降低，提升經濟效益，故本文將任務的處理時間和資源利用率作為成本約束條件。其中時間指標函數為：

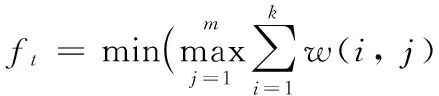
(17)

其中：m為資源數，k為第j個處理器上要處理任務的數量，w(i,j)表示第i個任務在第j個處理器上的時間損耗。資源利用率指標函數為：

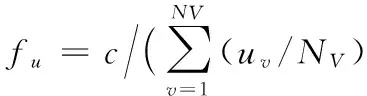
(18)

其中：NV為資源總數；uv表示第v個資源的綜合利用率；實驗發現資源利用率與時間消耗不處于同一數量級，因此采用加入權重c(本文取值15)的方式，使得二者數量級相同，因此調度代價適應度函數定義為：

Fd=min(α*ft+β*fu)

(19)

其中：α、β∈rand(0,1),α+β=1且α·β≠0。

為提升用戶滿意度，本文提出一種基于偏好的滿意度模型。將任務按屬性分為四類：計算型任務、帶寬型任務、存儲型任務和普通任務。計算型任務的評價準則為：

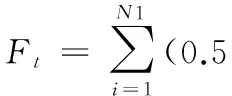
(20)

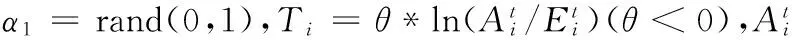
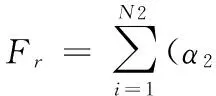
(21)

存儲型任務的評價準則：

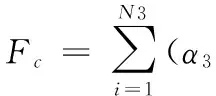
(22)

普通任務評價準則：

(23)

綜合評價準則定義為：

Ftotal=max(Δ-(Ft+Fr+Fc+Fp)/N)

(24)

N1、N2、N3、N4為各類任務的數量，且N1+N2+N3+N4=N,Δ為滿意度最優值，一般Δ=10。故本文的驅動模型為：

Fz=γ1*Ftotal-γ2*ε*Fd

(25)

其中：γ1、γ2為權重系數，ε為數量級調整系數。

2.6 算法流程

考慮任務數量大小對聚類效果的影響，算法設定任務數小于設定值NT(NT值取60～150時效果最佳)時直接采用改進的SOS算法，當任務數大于設定值NT時采用基于聚類的改進共生演算法——基于模糊C均值和改進共生演算法的云任務調度算法(Fuzzy c-means based and Improved Discrete Symbiotic Organisms Search algorithm, FIDSOS)，具體過程描述如下。

1)參數初始化：設置種群大小Scale、迭代次數K、終止條件及各項參數。

2)算法選擇與種群初始化：判斷任務數目是否大于設定閾值NT，大于則進入步驟3)，否則依據資源-任務整體編碼方式生成初始種群并進入步驟4)。

3)對任務和資源進行模糊聚類并對資源進行重排序，依據任務的聚類結構按照可變資源-任務間接編碼方生成初始種群，進行指導迭代后進入步驟4)。

4)依據改進DSOS算法對種群進行更新得到進化種群：

①按SOS算法過程對種群進行進化更新；

②對暫淘汰個體按式(7)進行更新操作；

③對當前優秀個體進行旋轉尋優操作。

5)判斷種群是否達到終止條件，達到則進入步驟6)；否則返回步驟4)。

6)得到調度結果，計算滿意度和調度代價。

3 實驗與分析

3.1 實驗環境及實驗參數

參考文獻[11-12]及[25-26]模擬搭建的云任務調度仿真系統及作者在文獻[27]所做的前期工作，利用Matlab實現一個云任務調度仿真系統。仿真系統主要由任務產生器、資源產生器、故障干擾產生器、調度器和評價器5部分組成。任務產生器產生任務向量，任務屬性包括任務大小等QoS因素，本文研究的是批任務。資源產生器可依據要求產生資源，資源屬性包括：CPU頻率(計算能力)、能提供的存儲空間、帶寬等。故障干擾產生器主要模擬網絡中可能出現的故障，作用于資源，可影響資源屬性。調度器接收到調度請求后對任務和可用資源進行標號并依據調度算法得到的結果將任務分配到資源上，然后更新節點值。評價器判斷調度結果是否滿足系統和用戶需求。

仿真系統模擬10～1 000個任務在處理器上的執行情況。通過控制任務產生器將任務長度控制在[500,1 500]范圍內，帶寬需求控制在[100,500]內，存儲需求控制在[200，1 000]內；同理，通過控制資源產生器，將資源的計算能力控制在[2 000,10 000]內，傳輸能力控制在[500,5 000]內，存儲能力控制在[500,5 000]內。各項指標均按一定規則在上述范圍內用模擬器隨機生成。

將本文算法與改進遺傳算法(Global Genetic Algorithm, GGA)、混合粒子群遺傳算法(Hybrid Particle Swarm Optimization and Genetic Algorithm, PSO-GA)和基本DSOS算法進行對比分析。優化目標為最小代價和用戶滿意度。實驗統一設置終止條件為最大迭代次數為400次或連續50次迭代差值小于0.001。算法具體參數參照表2。

表2 算法參數Tab. 2 Algorithm parameters

表3 不同任務數算法性能對比Tab. 3 Performance comparison with different number of tasks

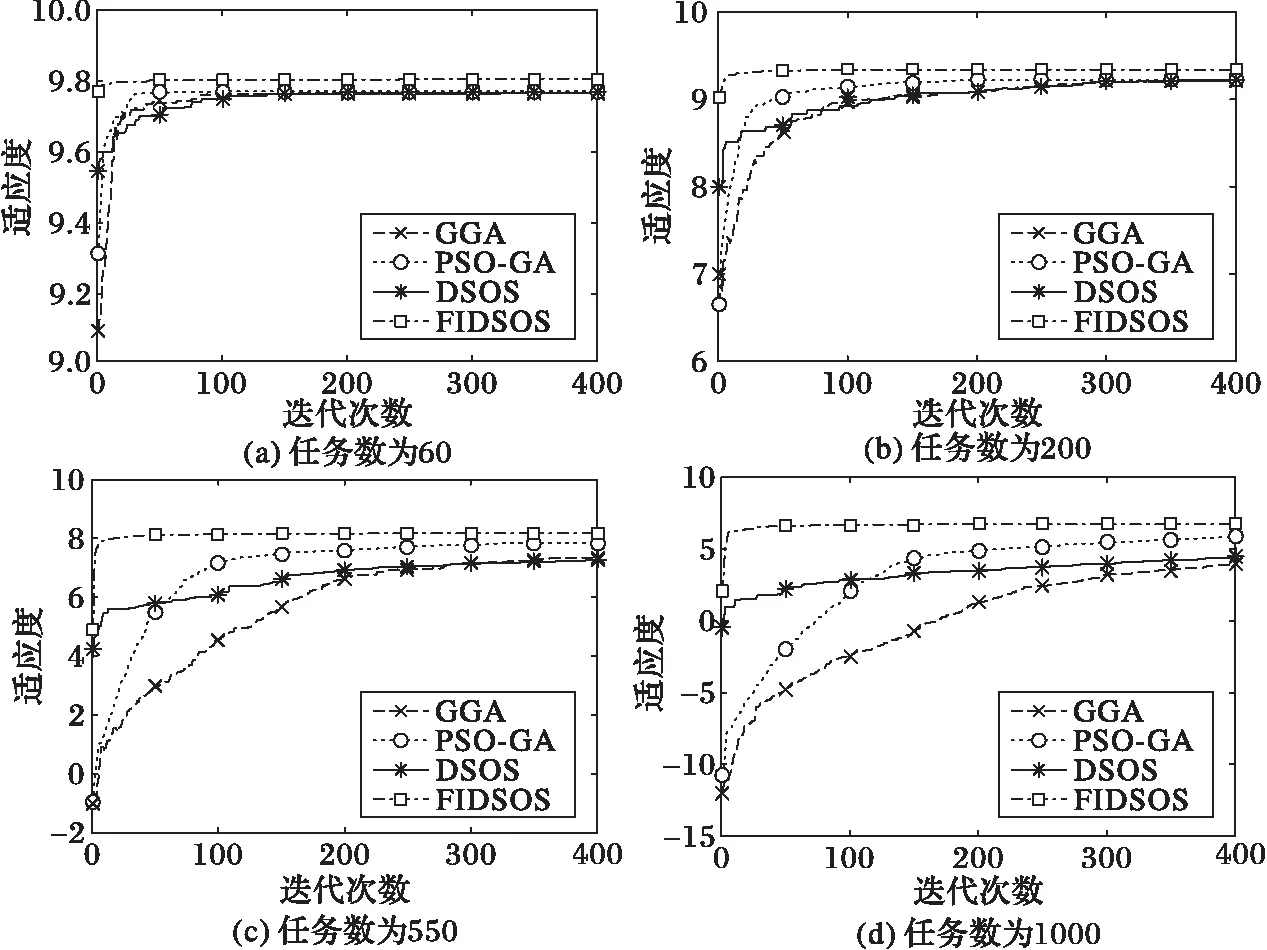
圖10 任務數不同時適應度和迭代次數對比 Fig. 10 Fitness and iteration comparison with different number of tasks

其中改進GA中:

(26)

(27)

其中：fmax為最大的適應度值，favg為平均適應度值，f′為要交叉的兩個個體中較大的適應度值，f為要變異個體的適應度值；PSO-GA算法中rand(0,1)代表在0～1隨機取值；本文算法中fb=2*π/k，k為當前迭代次數。

3.2 實驗結果分析

為防止特殊情況對實驗結果的影響，所有實驗各運行10次，記錄調度成本值和用戶滿意度并取10次的平均值作為最終結果。

系統生成8個虛擬機資源和10、20、60、100、150、200、550、1 000個數目的子任務集合進行實驗。

表3展示了任務數量為60和550時的算法性能，可知四種算法中GGA算法穩定性較差，其次為PSO-GA算法。DSOS算法和本文算法擁有較好的穩定性，且在任務數增加時本文穩定性所受影響較小。算法迭代次數和尋優能力對比如圖10所示，為方便說明任務數大小對算法的影響，選取對比任務數為60、200、550和1 000 四個數目。可看出當任務數較少時四種算法的尋優能力相差不大，隨著任務數的增加本文算法尋優能力優勢越發明顯。當任務數超過200后其他算法性能極度下降，性能下降最快的是遺傳算法，而本文算法依然保持著較好魯棒性和較強的尋優能力。遺傳算法更新個體上依靠交叉和變異，交叉點和變異點數目的選取影響著算法速度，隨著任務數目的增加若交叉點和變異點一成不變必然會導致算法尋優能力變差。而PSO算法和SOS算法依據各自的進化公式在相應的解空間上不斷搜索最優解，尋優所受影響勢必小于遺傳算法，但由于搜索的無目的性和評價函數的影響，在任務數增加時依然會使得尋優能力變差。本文算法對資源和任務進行模糊聚類后，能在解空間上具有目的性的搜索，使得算法尋優速度快且不會因為由于任務數的增加而使得算法性能加速下降。

尋優速度不能完全說明算法優劣，本文旨在最小化調度代價的同時最大化用戶滿意度。由圖11和圖12知，任務較少時本文算法與其他三種算法在調度代價和用戶滿意度上相差甚微，只有當任務數增加到60時差別才開始顯現，效果最差的為GGA算法，PSO-GA與DSOS算法效果相當，本文算法在調度代價和用戶滿意度上都有著較好結果。

隨著任務規模逐漸增加，算法差異開始變得明顯。由圖13可看出在調度代價上DSOS算法與PSO-GA算法尋優能力相當，GGA算法表現最差，本文算法保持最優；但在用戶滿意度上(如圖14所示)，DSOS算法與GGA算法相當，均劣于PSO-GA算法，本文算法保持最優且優勢愈發明顯。

傳統改進算法單一考慮系統性能或用戶滿意度，在以調度成本約束用戶滿意度的情況下可能產生不一樣的優化結果，算法性能無法保證。本文采用基于聚類和改進共生演的算法能夠在保持最小化調度代價的同時在解空間進行有目的性的搜索，可收斂到更優解，進而提高了用戶的滿意度。由此可見，FIDSOS算法具有更好的性能。

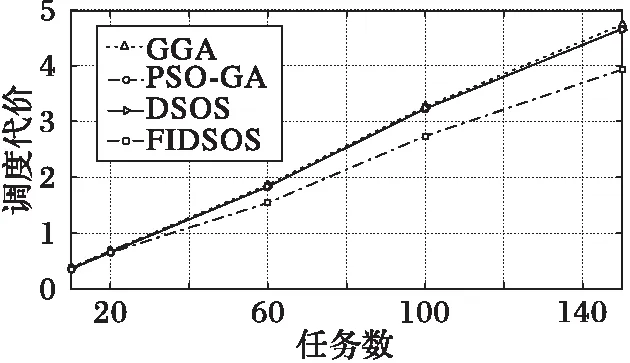
圖11 任務較少時算法調度代價對比 Fig. 11 Cost comparison with less tasks

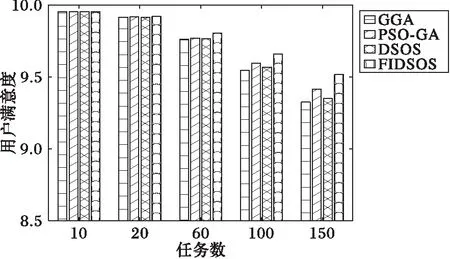
圖12 任務較少時用戶滿意度對比 Fig. 12 Satisfaction comparison with less tasks

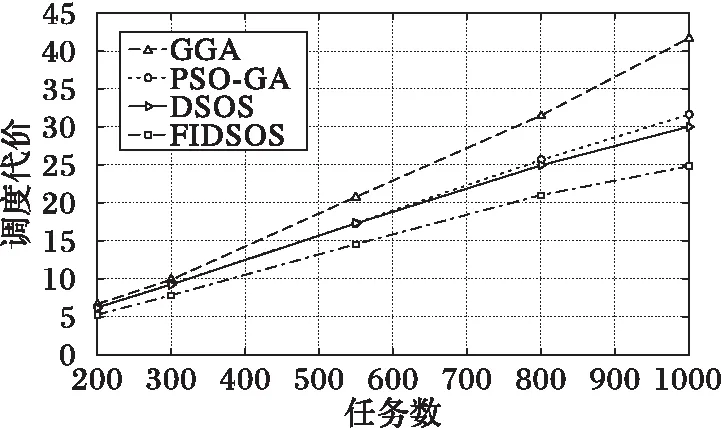
圖13 任務較多時算法調度代價對比 Fig. 13 Cost comparison with more tasks

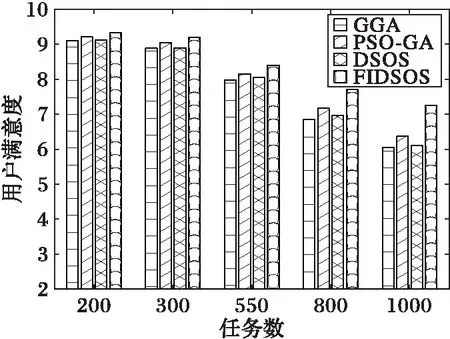
圖14 任務較多時用戶滿意度對比 Fig. 14 Satisfaction comparison with more tasks

4 結語

針對現有一些調度算法未將調度代價和用戶滿意度綜合考慮且容易陷入局部最優解、收斂慢的問題，提出一種在云環境下使用的任務調度算法。為提升算法精度，設置閾值NT，任務數量小于NT時直接采用改進共生演算法，任務數大于NT時采用基于聚類和改進的共生演算法。通過對任務和資源進行聚類，算法能對解空間進行目的性的搜索，進而提高算法的尋優速度。改進共生演算法考慮潛在優秀解可防止優秀解的丟失，最后對整個種群進行的旋轉尋優操作，減小了算法陷入局部最優的概率，加強了算法的尋優能力。實驗結果表明，相比改進的遺傳算法GGA、PSO-GA算法和DSOS算法，本文算法在保持高收斂性能的前提上能夠搜索到更為優秀的解，能夠實現較小調度成本且能夠提高用戶的滿意度。

參考文獻(References)

[1] FOSTER I, ZHAO Y,RAICU I, et al. Cloud computing and grid computing 360-degree compared [C]// GCE’08: Proceedings of the 2008 Grid Computing Environments. Washington,DC: IEEE Computer Society, 2008: 1-10.

[2] BOCHENINA K. A comparative study of scheduling algorithms for the multiple deadline-constrained workflows in heterogeneous computing systems with time windows [EB/OL]. [2017- 04- 12]. http://pdfs.semanticscholar.org/c88f/93f927d69432276665f53a5203c6987e8594.pdf.

[3] DURAO F,FONSEKA A,GARCIA V C, et al. A systematic review on cloud computing [J]. Journal of Supercomputing, 2014, 68(3): 1321-1346.

[4] AVRAM M G. Advantages and challenges of adopting cloud computing from an enterprise perspective [EB/OL]. [2017- 04- 12].https://core.ac.uk/download/pdf/82662807.pdf.

[5] AHMAD S G, LIEW C S, MUNIR E U, et al. A hybrid genetic algorithm for optimization of scheduling workflow applications in heterogeneous computing systems [J]. Journal of Parallel and Distributed Computing, 2016, 87(C): 80-90.

[7] BRATTON D, KENNEDY J. Defining a standard for particle swarm optimization [C]// Proceedings of the 2007 IEEE Swarm Intelligence Symposium. Washington, DC: IEEE Computer Society, 2007: 120-127.

[8] XUE S-J, WU W. Scheduling workflow in cloud computing based on hybrid partial swarm algorithm [J]. TELKOMNIKA : Indonesian Journal of Electrical Engineering, 2012,10(7): 1560-1566.

[9] BANSAL N, MAURYA A, KUMAR T, et al. Cost performance of QoS driven task scheduling in cloud computing [EB/OL]. [2017- 04- 15]. http://core.ac.uk/download/pdf/82232227.pdf.

[10] ARABNEJAD H, BARBOSA J G. Multi-QoS constrained and profit-aware scheduling approach for concurrent workflows on heterogeneous systems [J]. Future Generation Computer Systems, 2017,68: 211-221.

[11] 王娟,李飛,張路橋.PSO應用于QoS偏好感知的云存儲任務調度[J].通信學報,2014,35(3):231-238.(WANG J, LI F, ZHANG L Q. Apply PSO into cloud task scheduling with QoS preference awareness [J]. Journal on Communications, 2014, 35(3): 231-238.)

[12] GAMAL EL DIN HASSAN ALI H, SAROIT I A, KOTB A M. Grouped tasks scheduling algorithm based on QoS in cloud computing network [J]. Egyptian Informatics Journal, 2017, 18(1): 11-19.

[13] 杜曉麗,蔣昌俊,徐國榮,等.一種基于模糊聚類的DAG任務圖調度算法[J].軟件學報,2006,17(11):2277-2288.(DU X L, JIANG C J, XU G R, et al. A grid DAG scheduling algorithm based on fuzzy clustering [J]. Journal of Software, 2006, 17(11): 2277-2288.)

[14] 陳志剛,楊博.網絡服務資源多維性能聚類任務調度[J].軟件學報,2009,20(10):2766-2774.(CHEN Z G,YANG B. Task scheduling based on multidimensional performance clustering of grid service resources [J]. Journal of Software,2009, 20(10): 2766-2774.)

[15] 李文娟,張啟飛,平玲娣,等.基于模糊聚類的云任務調度算法[J].通信學報,2012,33(3):146-153.(LI W J, ZHANG Q F, PING L D, et al. Cloud scheduling algorithm based on fuzzy clustering [J]. Journal on Communications, 2012, 33(3): 146-153.)

[16] 郭鳳羽,禹龍,田生偉,等.云計算環境下對資源聚類的工作流任務調度算法[J].計算機應用,2013,33(8):2154-2157.(GUO F Y, YU L, TIAN S W, et al. Workflow task scheduling algorithm based on resource clustering in cloud computing environment [J]. Journal of Computer Applications, 2013, 33(8): 2154-2157.)

[17] DEAN J, GHEMAWAT S. MapReduce: simplified data processing on large clusters [C]// OSDI ’04: Proceedings of the 6th Conference on Symposium on Operating Systems Design and Implementation. Berkeley, CA: USENIX Association, 2004: 10.

[18] CHENG M Y, PRAYOGO D. Symbiotic organisms search: a new metaheuristic optimization algorithm [J]. Computer and Structures, 2014,139: 98-112.

[19] EZUGWU E S, ADEWUMI A O, FRINCU M E. Simulated annealing based symbiotic organisms search optimization algorithm for traveling salesman problem [J]. Expert Systems with Applications, 2017,77: 189-210.

[20] YU V F, REDI A A N P, YANG C L, et al. Symbiotic organisms search and two solution representations for solving the capacitated vehicle routing problem [J]. Applied Soft Computing, 2017, 52(C): 657-672.

[21] TEJANI G G, SAVSANI V J, PATEL V K. Adaptive Symbiotic Organisms Search (SOS) algorithm for structural design optimization [J]. Journal of Computational Design and Engineering, 2016, 3(3): 226-249.

[22] GUHA D, ROY P, BANERJEE S. Quasi-oppositional symbiotic organism search algorithm applied to load frequency control [J]. Swarm and Evolutionary Computation, 2016,33: 46-67.

[23] ABDULLAHI M, NGADI M A, ABDULHAMID S M. Symbiotic organism search optimization based task scheduling in cloud computing environment [J]. Future Generation Computer Systems, 2016,56: 640-650.

[24] BEZDEK J C. Pattern Recognition with Fuzzy Objective Function Algorithms [M]. Norwell, MA: Kluwer Academic Publishers, 1981:10-18.

[25] 王娟,李飛,劉兵,等.融合層次分析法的PSO云存儲任務調度算法[J].計算機應用研究,2014,31(7):2013-2016.(WANG J, LI F, LIU B, et al. AHP integrated PSO task scheduling algorithm in cloud storage system[J]. Application Research of Computers, 2014, 31(7): 2013-2016.)

[26] LI K. Scheduling parallel tasks with energy and time constraints on multiple manycore processors in a cloud computing environment [EB/OL]. [2017- 03- 01]. http://www.cs.newpaltz.edu/～lik/publications/Keqin-Li-FGCS-2017.pdf.

[27] 李昆侖,王珺,宋健,等.基于改進GEP和資源改變量的局部云任務調度算法[J].軟件學報,2015,26(S2):78-89.(LI K L, WANG J, SONG J, et al. Local cloud task scheduling algorithm based on improved GEP and change of resources [J]. Journal of Software, 2015, 26(S2): 78-89.)

This work is partially supported by the National Natural Science Foundation of China (61672205).

LIKunlun, born in 1962, Ph. D., professor. His research interests include pattern recognition, image processing, computer network, intelligent information processing.

GUANLiwei, born in 1990, M.S. candidate. His research interests include cloud computing task scheduling, virtualization.

GUOChanglong, born in 1991, M. S. candidate. His research interests include data mining, recommendation algorithm.