空間剛性梁軌道與姿態耦合動力學問題的辛分析

尹婷婷， 鄧子辰,2， 蔣憲宏

(1. 西北工業大學 力學與土木建筑學院，西安 710072； 2. 大連理工大學 工業裝備結構分析國家重點實驗室，遼寧 大連 116023)

梁的動力學問題是一個古老的力學問題，一直備受學術界關注。在過去的一個多世紀中，歐拉-伯努利梁模型和鐵木辛柯梁模型相繼被提出，并用于描述柔性梁的動力學問題，取得了一系列的創新性成果。以上兩種經典梁理論所不同的是，歐拉-伯努利梁模型在描述梁的動力學問題時基于以下假設：梁只有彎曲變形,而梁對剪切變形完全剛性,即忽略了剪切變形和轉動慣量；而鐵木辛柯梁模型則考慮剪切變形與轉動慣量。從模型的完備性方面看，鐵木辛柯梁模型能夠更好地描述柔性梁的動力學問題。

空間梁動力學問題相較于傳統梁動力學問題[1]，具有以下特點：① 空間梁邊界條件可以設定為兩端自由邊界，而經典梁模型通常包括簡支、固支等情形；② 空間梁需要考慮大范圍運動與姿態及結構振動間的耦合效應，而經典梁模型僅僅考慮結構振動問題；③ 空間梁由于所處工作環境復雜，因此所受載荷相對復雜。由于以上的特點，空間梁的動力學問題已經引起了力學界的廣泛關注：Silva等[2-3]在考慮重力梯度影響的基礎上，給出了空間柔性梁的建模方法和數值模擬結果，首開空間梁動力學問題的研究先河；Chen等[4]開展了關于空間柔性梁的幾何非線性分析，得到了一些有意義的結果；Quadrelli等[5]基于多體動力學理論，采用混合變分方法研究了空間梁的動力學行為，其研究成果對于本文數值結果的分析具有一定的參考意義；劉錦陽等[6]基于連續介質理論，建立了大范圍運動空間梁耦合動力學模型，并初步仿真分析了空間梁的耦合效應；Zhang等[7-8]采用歐拉-伯努利梁模型分析了空間剛柔耦合結構的動力學行為，將剛柔耦合動力學分析思想引入空間結構分析，具有廣泛的應用前景；最近，Hu等考慮大跨度空間柔性阻尼梁的結構、姿態與軌道耦合問題，建立了動力學方程模型，并采用廣義多辛分析方法[9-10]得到了空間柔性阻尼梁的阻尼效應及其平衡態條件，為本文的建模過程提供了理論依據。

在針對大跨度空間柔性阻尼梁的保結構分析過程中，由于構件跨度大，因此構件的柔性將不容忽視，也就是構件的柔性變形及振動不可忽略。不可否認，空間結構中大跨度的梁結構是比較常見的[11]，同時也應該意識到，空間結構中許多連接件的結構跨度比較小且相對剛度較大，這類構件在軌組裝之前，如果依然采用已有文獻[12]的建模和分析方法，雖然能使得動力學分析結果更為精確，但是將大大增加計算復雜度，無法為構件的實時軌道和姿態主動控制預留足夠的時間，以致于無法及時完成組裝過程。因此，在實際工程中，這類構件可以簡化為剛性梁然后開展動力學行為分析，并忽略其阻尼效應。基于此，本文將針對空間剛性梁的平面運動與自身姿態之間的強耦合問題，采用辛數學方法[13]分析空間剛性梁的耦合動力學特性，為空間結構構件的主動控制設計提供參考。

1 空間剛性梁的耦合動力學模型

考慮一剛性梁的軌道與姿態耦合問題，如圖1所示。假定剛性梁受地球中心引力場作用，只考慮其在平面軌道上做面內運功，忽略太陽光壓、大氣阻力、日月引力等攝動力的影響。假定該剛性梁運行在地球同步軌道上，建立地球赤道平面的慣性極坐標系：以地心O為坐標系的極點，極軸OX指向春分點，空間剛性梁的質心位置M可用極坐標表示為(r,θ)，r為質心M到地心O的距離，并稱為極徑，θ為極軸OX與OM之間的夾角，并稱為極角。此外，以軸線OM與空間剛性梁之間的夾角α描述空間梁的姿態變化。

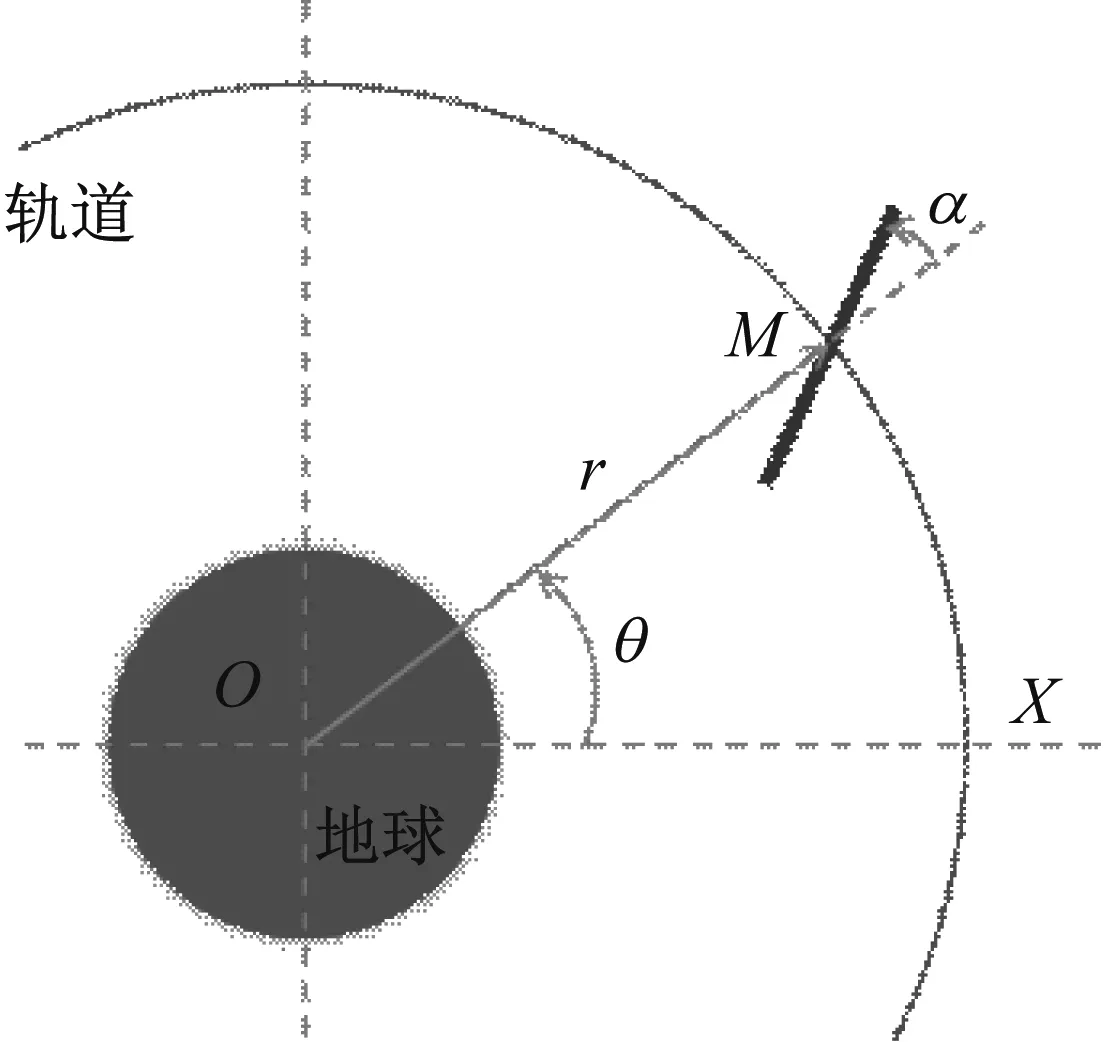
圖1 空間剛性梁軌道與姿態耦合動力學模型

簡化的空間剛性梁模型長度為l，線密度為ρ，其空間位形可用極坐標描述為

q=[q1q2q3]T=[rθα]T

三個廣義坐標的物理意義分別為：r表示空間剛性梁模型在軌運行的軌道半徑；θ表示空間剛性梁質心的軌道轉角(即真近角)；α表示空間剛性梁模型的姿態角。

空間剛性梁模型系統的動能可以表示為

(1)

系統勢能可以表示為[14]

(2)

式中：μ為地球引力常數，勢能表達式中的第二項為引力梯度近似項，在梁的跨度不大的情況下，可以忽略其他引力梯度高階項。

引入Lagrange函數

(3)

根據第二類Lagrange方程

(4)

可以推導得到空間剛性梁模型的動力學控制方程

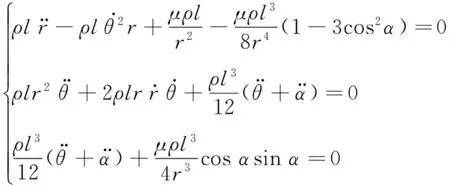
(5)

方程式(5)是一個高度非線性的二階微分方程組，由于受到萬有引力梯度的影響，空間剛性梁模型的軌道坐標和姿態坐標耦合在一起，這為空間剛性梁的動力學分析帶來了極大的不便。

2 辛分析方法

上一節已提到，方程式(5)是一個強非線性系統，無法采用現有的理論得到其解析解，因此，空間剛性梁的軌道與姿態耦合動力學分析必須借助于合適的數值分析方法。由于空間結構構件的一個突出需求就是其在軌服役時間長，因此，所使用的數值分析方法需要具有長時間的數值穩定性，而保結構分析方法正好能夠滿足這一特殊的需求。

保結構分析方法起源于馮康院士提出的辛幾何算法[15]，近年來已經發展推廣至針對無限維動力學系統的(廣義)多辛分析方法[16]，并逐漸形成了較為完整的理論體系。馮康院士在提出辛幾何算法的初期，就已經開始嘗試將辛幾何算法應用于天體力學的研究，并對天體運動行為進行了長時間的預測，這為本文的研究工作奠定了理論基礎。

(6)

龍格庫塔方法由于其程序模塊化程度高，穩定性好，備受計算數學家的青睞。然而，從保結構的觀點看，龍格庫塔方法并不能自動保辛，因此，Feng[17]通過添加人工約束，使得龍格庫塔方法在某些特殊情形下滿足保辛要求，從而發展成了辛龍格庫塔方法。以下就從傳統龍格庫塔方法出發，簡要介紹辛龍格庫塔方法。s級的經典龍格庫塔方法的一般格式為

(7)

Sanz-Serna等[18]已經證明式(7)是辛的，當且僅當其系數滿足如下的條件

bibj-aijbi-ajibj=0

(8)

式中：i,j=1,2,…,s。

在式(8)中，當系數aij、bi取不同的值時，可以得到不同的辛龍格庫塔格式。一種常用的2級4階辛龍格庫塔格式，其系數aij、bi取值為

(9)

采用2級4階辛龍格庫塔方法離散對偶方程式(6)，即可得到剛性梁軌道與姿態耦合動力學模型的辛龍格庫塔格式。

3 數值實驗

圖2 軌道半徑擾動量的演化情況

圖3 真近角的演化情況

圖4 姿態角的演化情況

從圖2～圖4中不難發現，當初始姿態角速度為零時，剛性梁的圓周運動與自身的轉動之間沒有發現顯著的耦合效應，這是因為由于梁的尺寸很小，引力梯度的影響難以在數值結果中得到體現；當初始姿態角速度不為零時，剛性梁軌道與姿態之間的耦合效應比較明顯，隨著初始姿態角速度的增大，軌道半徑擾動增大，剛性梁圓周運動周期縮短(表現為真近角增長速度的增大)，姿態角振動幅值略有減小(為了反映出振動幅值略有減小的趨勢，在圖4中將姿態角的模擬時間延長至2 160 h)。

以上模擬結果從一定程度上反映了剛性梁軌道與姿態之間的耦合效應，這些耦合效應還需要得到試驗的進一步驗證。然而，空間剛性梁的試驗耗資巨大，因此，本文將從另一個角度對以上結果加以驗證。我們注意到，式(5)是一個嚴格的保守動力學系統，而辛方法的最大優點就是能夠長時間保持系統的整體能量，因此，在模擬過程中記錄每一時間步的系統總能量

(10)

然后，得到每一時間步的總能量值與初始時刻能量值之間的相對誤差，記為

以case 3情形為例，得到的每個時間點的總能量相對誤差如圖5(a)所示。為了與辛方法做對比，展現辛方法的保結構優勢，本文同時采用傳統四階龍格庫塔格式模擬空間剛性梁的空間運動與姿態演化，在模擬過程中記錄總能量相對誤差，所得到的能量相對誤差如圖5(b)所示。

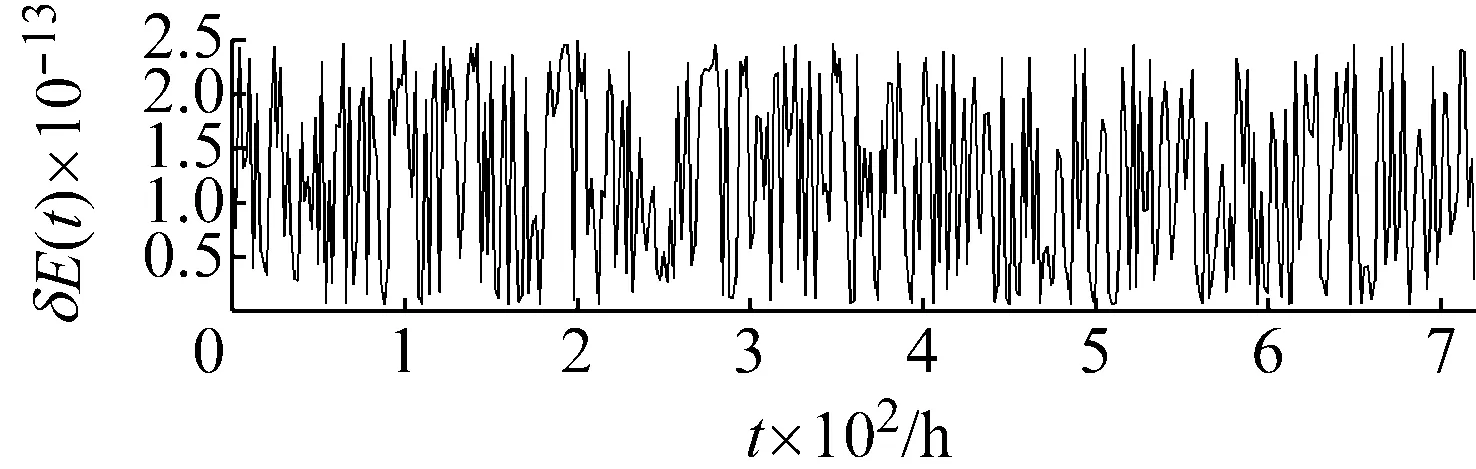
(a) 辛方法能量相對誤差結果

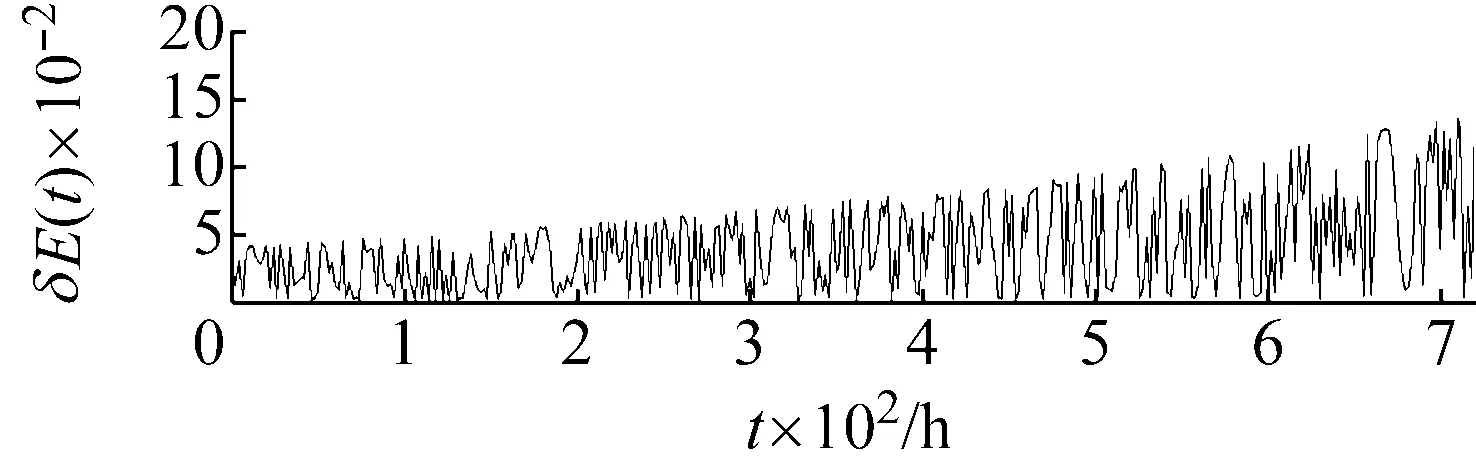
(b) 龍格庫塔方法能量相對誤差結果

從圖5中可以看出，采用辛分析方法能夠長時間保持系統總能量這一守恒量；而使用傳統四階龍格庫塔格式得到的系統總能量相對誤差的數量級遠高于使用辛方法所得到的對應結果，并且隨著模擬時間的延長，誤差累積明顯，當模擬時長至700 h后，累積的能量相對誤差超過10%。以上結果間接地證明了相對于傳統的龍格庫塔方法，本文采用辛方法得到的剛性梁軌道與姿態耦合效應的數值結果是可信的。

4 結 論

近年來，空間柔性梁模型及數值分析方法引起了學術界的廣泛關注，然而，空間柔性梁的動力學模型異常復雜，相應的數值分析方法效率不高，這難以滿足結構主動控制的要求，為此，本文著眼于空間結構中某些大剛度小尺寸連接件，這些連接件在軌組裝之前的動力學模型沒有必要采用柔性梁模型進行動力學分析，本文將其簡化為空間剛性梁，建立了其軌道與姿態相互耦合的動力學模型。針對建立的動力學模型，采用辛龍格庫塔方法進行了剛性梁的耦合動力學分析，得到了如下結論：

(1) 當剛性梁的初始姿態角速度為零時，從數值結果中無法體現出姿態與軌道的耦合效應，其原因是，相對于軌道半徑，剛性梁的尺寸極小，引力梯度的影響難以在本文數值結果中得到體現。這種情形下姿態與軌道耦合效應尚需要發展更為精確的數值方法加以分析。

(2) 隨著剛性梁初始姿態角速度的增大，剛性梁的姿態與軌道耦合效應將愈發明顯，耦合效應體現在：隨著初始姿態角速度的增大，軌道半徑擾動增大，真近角增長速度的增大，姿態角振動幅值略有減小。

以上結論的正確性從文中最后關于系統總能量相對誤差的結果中得到間接證明，同時，數值方法的長時間穩定性也得到了相應的檢驗。

參 考 文 獻

[1] 劉錦陽, 洪嘉振. 大范圍運動空間梁的耦合動力學模型[J]. 上海交通大學學報, 2003, 37(4):532-534.

LIU Jinyang, HONG Jiazhen. Coupling dynamic modeling of the spatial beam undergoing large overall motions[J]. Jornal of Shanghai Jiao Tong University, 2003, 37(4):532-534.

[2] SILVA M R C, ZARETZKY C L. Nonlinear dynamics of a flexible beam in a central gravitational field—I. Equations of motion[J]. International Journal of Solids and Structures, 1993, 30(17):2287-2299.

[3] SILVA M R C, ZARETZKY C L. Nonlinear dynamics of a flexible beam in a central gravitational field—II. Nonlinear motions in circular orbit[J]. International Journal of Solids and Structures, 1993, 30(17):2301-2316.

[4] CHEN Z Q, AGAR T J A. Geometric nonlinear analysis of flexible spatial beam structures[J]. Computers & Structures, 1993, 49(6):1083-1094.

[5] QUADRELLI B, ATLURI S. Analysis of flexible multibody systems with spatial beams using mixed variational principles[J]. International Journal for Numerical Methods in Engineering, 1998, 42(6):1071-1090.

[6] 劉錦陽, 李彬, 洪嘉振. 作大范圍空間運動柔性梁的剛-柔耦合動力學[J]. 力學學報, 2006, 38(2):276-282.

LIU Jinyang, LI Bin, HONG Jiazhen. Rigid-flexible coupling dynamics of a flexible beam with three-dimensional large overall motion[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(2):276-282.

[7] ZHANG Z G, QI Z H, WU Z G, et al. A spatial Euler-Bernoulli beam element for rigid-flexible coupling dynamic analysis of flexible structures[J]. Shock and Vibration, 2015(2): 1-15.

[8] 張志剛, 齊朝暉, 吳志剛, 等. 考慮變形耦合的幾何非線性空間梁單元[J]. 計算力學學報, 2014, 31(5):603-608.

ZHANG Zhigang, QI Zhaohui, WU Zhigang, et al. A geometrical nonlinear space beam element with considering deformation coupling[J]. Chinese Journal of Computational Mechanics, 2014, 31(5):603-608.

[9] HU W P, DENG Z C, HAN S M, et al. Generalized multi-symplectic integrators for a class of Hamiltonian nonlinear wave PDEs[J]. Journal of Computational Physics, 2013, 235(4):394-406.

[10] 胡偉鵬, 鄧子辰, 吳子燕, 等. 橋梁在移動荷載作用下動力學響應的廣義多辛算法[J]. 振動與沖擊, 2008, 27(4):66-69.

HU Weipeng, DENG Zichen, WU Ziyan, et al. Generalized multi-symplectic method for bridges subjected to moving loads[J]. Journal of Vibration and Shock, 2008, 27(4):66-69.

[11] 徐圣, 劉錦陽, 余征躍. 幾何非線性空間梁的動力學建模與實驗研究[J]. 振動與沖擊, 2014, 33(21):108-113.

XU Sheng, LIU Jinyang, YU Zhengyue. Dynamic modeling and tests for a geometric nonlinear spatial beam[J]. Journal of Vibration and Shock, 2014, 33(21):108-113.

[12] HU W P, LI Q J, JIANG X H, et al. Coupling dynamic behaviors of spatial flexible beam with weak damping[J]. International Journal for Numerical Methods in Engineering, 2017, 111: 660-675.

[13] 劉鐵權，鄧子辰， 周加喜. 基于辛數學方法的一維聲子晶體禁帶計算[J]. 振動與沖擊, 2010, 29(12):102-105.

LIU Tiequan, DENG Zichen, ZHOU Jiaxi. Symplectic method for calculation of band gap of one-dimensional phononic crystals[J]. Journal of Vibration and Shock, 2010, 29(12):102-105.

[14] 鄧子辰, 曹珊珊, 李慶軍, 等. 基于辛 Runge-Kutta 方法的太陽帆塔動力學特性研究[J]. 中國科學(技術科學), 2016, 46: 1242-1253.

DENG Zichen, CAO Shanshan, LI Qingjun, et al. Dynamic behavior of sail tower SPS based on the symplectic Runge-Kutta method[J]. Scientia Sinica(Technologica), 2016, 46:1242-1253.

[15] FENG K. On difference schemes and symplectic geometry[C]//Proceeding of the 1984 Beijing Symposium on Differential Geometry and Differential Equations. Beijing: Science Press, 1984: 42-58.

[16] BRIDGES T J. Multi-symplectic structures and wave propagation[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1997, 121(1):147-190.

[17] FENG K. Difference-schemes for Hamiltonian-Formalism and symplectic-geometry[J]. Journal of Computational Mathematics, 1986, 4(3):279-289.

[18] SANZ-SERNA J M. Runge-Kutta schemes for Hamiltonian systems[J]. BIT Numerical Mathematics, 1988, 28(4):877-883.