基于局域共振聲子帶隙的扭轉(zhuǎn)減振器設(shè)計(jì)方法

吳昱東， 李人憲， 丁渭平， 楊明亮， 馬逸飛

(西南交通大學(xué) 機(jī)械工程學(xué)院， 成都 610031)

動(dòng)力傳動(dòng)系扭轉(zhuǎn)振動(dòng)是汽車(chē)車(chē)內(nèi)振動(dòng)與噪聲的重要激勵(lì)源之一，可引起變速器齒輪敲擊異響(Gear Rattle Noise)[1]、車(chē)內(nèi)轟鳴聲(Booming Noise)[2]等噪聲問(wèn)題，降低汽車(chē)乘坐舒適性，嚴(yán)重時(shí)，甚至?xí)l(fā)傳動(dòng)軸系斷裂、變速器損壞，威脅車(chē)內(nèi)乘員安全[3]。自汽車(chē)產(chǎn)生以來(lái)，人們就在不斷探索各種控制傳動(dòng)系扭轉(zhuǎn)振動(dòng)的方法，安裝橡膠扭轉(zhuǎn)減振器就是其中常用的一種。由于對(duì)單一扭轉(zhuǎn)振動(dòng)峰值衰減效果較好，結(jié)構(gòu)簡(jiǎn)單、成本較低，橡膠扭轉(zhuǎn)減振器被廣泛用于汽車(chē)發(fā)動(dòng)機(jī)曲軸及傳動(dòng)系扭轉(zhuǎn)減振[4]。

目前，在扭轉(zhuǎn)減振器減振特性設(shè)計(jì)研究中，對(duì)固有頻率特性研究較多[5-6]，而對(duì)減振頻帶范圍的研究較少，因此工程應(yīng)用中，涉及扭轉(zhuǎn)減振器減振頻率范圍設(shè)計(jì)時(shí)，往往根據(jù)經(jīng)驗(yàn)來(lái)確定。近年來(lái)，聲學(xué)超材料以其可通過(guò)亞波長(zhǎng)尺寸結(jié)構(gòu)實(shí)現(xiàn)對(duì)低頻機(jī)械波有效控制的特性，吸引了大量物理學(xué)、材料學(xué)等學(xué)科的研究學(xué)者[7-10]，局域共振型聲子晶體作為聲學(xué)超材料中的一員，其帶隙及波導(dǎo)理論也逐漸清晰[11-15]。由于局域共振聲子晶體與扭轉(zhuǎn)減振器均是通過(guò)共振單元諧振將振動(dòng)能量局域化，阻隔其傳播，兩者具有相似的減振機(jī)理，因此局域共振聲子晶體帶隙理論研究的不斷深入也為扭轉(zhuǎn)減振器的設(shè)計(jì)方法提供的新的思路。

本文嘗試基于局域共振聲子晶體帶隙理論，研究扭轉(zhuǎn)減振器的減振頻帶特性，據(jù)此提出扭轉(zhuǎn)減振器減振帶隙的設(shè)計(jì)計(jì)算方法，并將該方法應(yīng)用于汽車(chē)動(dòng)力傳動(dòng)系扭振實(shí)際工程問(wèn)題。

1 扭轉(zhuǎn)減振器減振帶隙機(jī)理

1.1 扭轉(zhuǎn)減振器帶隙機(jī)理分析

如圖1所示為扭轉(zhuǎn)減振器結(jié)構(gòu)示意圖，扭轉(zhuǎn)減振器從內(nèi)到外一般由扭轉(zhuǎn)減振器所安裝軸系、橡膠圈和外圈三部分組成。根據(jù)其結(jié)構(gòu)可建立圖2所示扭轉(zhuǎn)減振器當(dāng)量簡(jiǎn)化模型，當(dāng)頻率為ω的扭轉(zhuǎn)振動(dòng)波傳遞至扭轉(zhuǎn)減振器所安裝軸系(即基體)時(shí)，根據(jù)牛頓第二定律，分別對(duì)基體及扭轉(zhuǎn)減振器外圈(即振子)建立平衡方程如式(1)及式(2)所示。

T-T′=(iω)2I0θ

(1)

T′=(iω)2I1α

(2)

式中：T為入射扭轉(zhuǎn)波對(duì)基體的作用轉(zhuǎn)矩;T′為振子對(duì)基體的反作用力矩;I0為基體轉(zhuǎn)動(dòng)慣量;I1為振子轉(zhuǎn)動(dòng)慣量;θ及α分別為基體和振子的角位移。

對(duì)于扭轉(zhuǎn)減振器振子，根據(jù)胡克定律有

-T′=K1(α-θ)

(3)

式中:K1為扭轉(zhuǎn)減振器橡膠圈的扭轉(zhuǎn)剛度。

將式(2)及式(3)代入式(1)中，可得

(4)

若將基體、振子及橡膠圈看成一個(gè)具有等效轉(zhuǎn)動(dòng)慣量的整體結(jié)構(gòu)，式(4)可以表示為

T=(iω)2Ieffθ

(5)

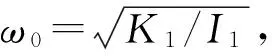
(6)

對(duì)于該整體結(jié)構(gòu)，其角位移頻率響應(yīng)函數(shù)為

(7)

則該系統(tǒng)的等效轉(zhuǎn)動(dòng)慣量及角位移頻響函數(shù)隨入射扭轉(zhuǎn)波頻率的變化曲線如圖3所示。

圖3 等效轉(zhuǎn)動(dòng)慣量及角位移頻響函數(shù)隨頻率變化關(guān)系

Fig.3 Equivalent rotational inertia and frequency response function of angular displacement change with frequency

若將該扭轉(zhuǎn)減振器視為一局域共振聲子晶體晶胞，則動(dòng)態(tài)等效轉(zhuǎn)動(dòng)慣量較大的頻率區(qū)域?qū)?yīng)局域共振帶隙產(chǎn)生的頻率范圍，而系統(tǒng)在零等效慣量點(diǎn)發(fā)生共振，意味著帶隙的結(jié)束；實(shí)際中，振動(dòng)衰減到一定程度即可認(rèn)為是帶隙，所以帶隙的截止頻率低于零等效慣量點(diǎn)對(duì)應(yīng)的頻率。從圖3可看出，在該帶隙范圍內(nèi)，角位移頻響函數(shù)較小，振動(dòng)衰減明顯，因此扭轉(zhuǎn)減振器減振頻帶特性與基于聲子晶體理論的扭轉(zhuǎn)減振器(晶胞)帶隙是一致的，增大零等效慣量點(diǎn)與局域共振點(diǎn)之間的距離，將會(huì)使帶隙的寬度增加。

1.2 扭轉(zhuǎn)減振器帶隙計(jì)算方法

由于局域共振聲子晶體帶隙可以表達(dá)扭轉(zhuǎn)減振器減振頻帶特性，因此可基于聲子晶體理論，計(jì)算扭轉(zhuǎn)減振器的減振帶隙。對(duì)于圖1所示橡膠扭轉(zhuǎn)減振器結(jié)構(gòu)(局域共振聲子晶體晶胞)，在扭轉(zhuǎn)波激勵(lì)下，該晶胞繞軸線x扭轉(zhuǎn)振動(dòng)，波動(dòng)方程為[16]

(8)

由于局域共振聲子晶體帶隙由晶胞結(jié)構(gòu)決定，與其排列周期數(shù)無(wú)關(guān)，因而可在無(wú)限周期結(jié)構(gòu)中計(jì)算該晶胞帶隙[17]，則第n個(gè)晶胞的解可以寫(xiě)成

θ(xn,t)=T(t)Θ(xn)=

eiωt[Ansin(qxn)+Bncos(qxn)]

(9)

假設(shè)n第個(gè)局域共振結(jié)構(gòu)中金屬環(huán)的扭轉(zhuǎn)位移為

φn(t)=Vneiωt

(10)

式中:Vn為第n個(gè)振子的振幅。對(duì)于第n個(gè)振子的慣量矩，根據(jù)力矩平衡得到

(11)

將式(9)和式(10)代入式(11)中得到

(12)

由第n-1個(gè)晶胞和第n個(gè)晶胞之間的位移連續(xù)和扭轉(zhuǎn)連續(xù)得到

Bn=An-1sin(qa)+Bn-1cos(qa)

(13)

An+FBn=An-1cos(qa)-Bn-1sin(qa)

(14)

式中:F=ω2IK/μ0JtqK-Iω2。

將式(13)及式(14)寫(xiě)成矩陣形式為

ψn=Mψn-1

(15)

式中:ψn=[An,Bn]T

M=

(16)

即為傳遞矩陣，可以求解到解析的色散關(guān)系

(17)

式中:k為Bloch波矢。對(duì)于任意給定的頻率ω，利用式(17)可以求得對(duì)應(yīng)的k值，即可獲得聲子晶體即扭轉(zhuǎn)減振器的帶隙特性。

為具體說(shuō)明該計(jì)算方法的使用，取基體材料為鋼，半徑r0為25 mm，軸向長(zhǎng)度a為60 mm；橡膠圈材料為硫化橡膠，外圈半徑r1為40 mm，軸向長(zhǎng)度l1為30 mm；振子材料為鋼，外圈半徑r2為50 mm，軸向長(zhǎng)度l2為30 mm，則根據(jù)式(17)計(jì)算獲得扭轉(zhuǎn)減振器能帶結(jié)構(gòu)如圖4所示。可以看出，該扭轉(zhuǎn)減振器可在50～120 Hz內(nèi)形成減振帶隙，抑制扭轉(zhuǎn)振動(dòng)的傳播。

圖4 能帶結(jié)構(gòu)圖

2 設(shè)計(jì)參數(shù)對(duì)扭轉(zhuǎn)減振器帶隙影響

2.1 幾何參數(shù)對(duì)扭轉(zhuǎn)減振器帶隙影響

對(duì)于上述簡(jiǎn)易橡膠扭轉(zhuǎn)減振器而言，其幾何設(shè)計(jì)參數(shù)主要包括基體半徑r0，軸向長(zhǎng)度a；橡膠圈外圈半徑r1，軸向長(zhǎng)度l1；振子外圈半徑r2，軸向長(zhǎng)度l2。基于圖4所示扭轉(zhuǎn)減振器，進(jìn)行幾何參數(shù)對(duì)扭轉(zhuǎn)減振器帶隙影響的靈敏度分析，結(jié)果如圖5所示。

從圖5可以看出，隨著基體半徑的增大，扭轉(zhuǎn)減振器減振帶隙下界升高，而上界則變化很小，帶隙變窄；當(dāng)橡膠圈外徑增大時(shí)，帶隙下界升高，上界降低，帶隙寬度減小；當(dāng)振子外圈半徑增大時(shí)，帶隙上下界都降低，但下界降低幅度較大，帶隙變寬；當(dāng)基體軸向長(zhǎng)度變大，帶隙下界不變，而上界降低，帶隙寬度減小；當(dāng)橡膠圈軸向長(zhǎng)度增大，帶隙上下界都升高，帶隙寬度變大；當(dāng)振子軸向長(zhǎng)度增大時(shí)，帶隙上下界都降低，其中下界降低幅度更大，因此帶隙變寬。

2.2 材料參數(shù)對(duì)扭轉(zhuǎn)減振器帶隙影響

橡膠扭轉(zhuǎn)減振器材料設(shè)計(jì)參數(shù)主要包括在基體材料的彈性模量、密度，橡膠圈的材料彈性模量以及振子材料的密度。如圖6所示為各材料參數(shù)對(duì)扭轉(zhuǎn)減振器帶隙影響的靈敏度分析結(jié)果。

由圖6可看出，當(dāng)基體材料密度增大時(shí)，扭轉(zhuǎn)減振器帶隙下界基本不變，上界降低，因此帶隙變窄；隨著振子材料密度增大，帶隙上下界都降低，其中下界降低幅度更大，帶隙變寬；基體材料的彈性模量對(duì)扭轉(zhuǎn)減振器帶隙基本沒(méi)有影響；當(dāng)橡膠圈材料彈性模量增大時(shí)，帶隙上下界都升高，上界上升幅度較大，帶隙寬度增大。

(a) 基體半徑對(duì)帶隙影響

(b) 橡膠圈外圈半徑對(duì)帶隙影響

(c) 振子外圈半徑對(duì)帶隙影響

(d) 基體軸向長(zhǎng)度對(duì)帶隙影響

(e) 橡膠圈軸向長(zhǎng)度對(duì)帶隙影響

(f) 振子軸向長(zhǎng)度對(duì)帶隙影響

(a) 基體密度對(duì)帶隙影響

(b) 振子密度對(duì)帶隙影響

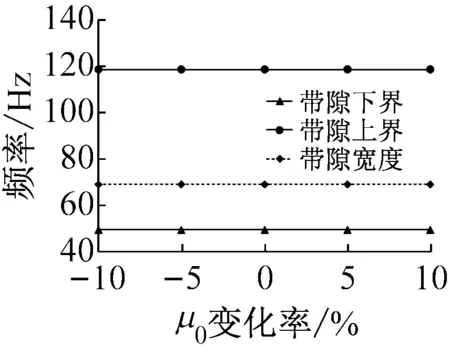
(c) 基體彈性模量對(duì)帶隙影響

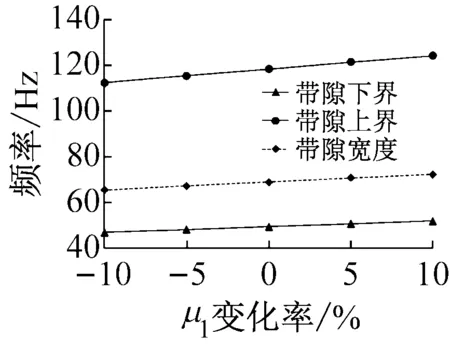
(d) 橡膠圈彈性模量對(duì)帶隙影響

3 扭轉(zhuǎn)減振器設(shè)計(jì)方法應(yīng)用

某國(guó)產(chǎn)前置后驅(qū)MPV車(chē)在加速行駛過(guò)程中，由于傳動(dòng)系扭轉(zhuǎn)振動(dòng)劇烈，引致車(chē)內(nèi)出現(xiàn)明顯轟鳴聲問(wèn)題，嚴(yán)重影響車(chē)輛乘坐舒適性，其傳動(dòng)系扭轉(zhuǎn)振動(dòng)及車(chē)內(nèi)噪聲測(cè)試結(jié)果如圖7與圖8所示(黑實(shí)線所示)。從圖中可以看出，在該車(chē)加速過(guò)程中，當(dāng)發(fā)動(dòng)機(jī)轉(zhuǎn)速達(dá)到1 500 r/min附近時(shí)，傳動(dòng)系扭轉(zhuǎn)振動(dòng)十分劇烈，相應(yīng)地，此時(shí)車(chē)內(nèi)噪聲聲壓級(jí)也出現(xiàn)明顯峰值。

為解決該車(chē)傳動(dòng)系扭振引致的車(chē)內(nèi)轟鳴聲問(wèn)題，選擇使用橡膠扭轉(zhuǎn)減振器抑制其傳動(dòng)系扭振。該車(chē)加速過(guò)程中，發(fā)動(dòng)機(jī)(4缸)轉(zhuǎn)速在1 300～1 700 r/min范圍內(nèi)時(shí)動(dòng)力傳動(dòng)系扭振較為劇烈，對(duì)應(yīng)其扭振2階激勵(lì)頻率范圍為43～57 Hz。則根據(jù)式(17)計(jì)算分析可得，當(dāng)扭轉(zhuǎn)減振器基體材料為鋼，半徑為55 mm，軸向長(zhǎng)度60 mm；橡膠圈材料為硫化橡膠，半徑為70 mm，軸向長(zhǎng)度18 mm；振子材料為鋼，半徑為82 mm，軸向長(zhǎng)度為35 mm時(shí)，其減振帶隙下界為41.3 Hz，上界為63.1 Hz，帶隙寬度為21.8 Hz，可有效覆蓋傳動(dòng)系扭振的峰值范圍。試制扭轉(zhuǎn)減振器樣件，將其安裝于主減速器輸入軸處(如圖9所示)，并進(jìn)行整車(chē)傳動(dòng)系扭轉(zhuǎn)振動(dòng)及車(chē)內(nèi)噪聲測(cè)試，測(cè)試結(jié)果如圖7及圖8所示。從圖中可以看出，安裝扭轉(zhuǎn)減振器后，當(dāng)發(fā)動(dòng)機(jī)轉(zhuǎn)速位于1 500 r/min附近時(shí)，傳動(dòng)系扭轉(zhuǎn)振動(dòng)得到了有效抑制，車(chē)內(nèi)噪聲聲壓級(jí)降低，同時(shí)主觀感受也無(wú)明顯轟鳴聲出現(xiàn)。

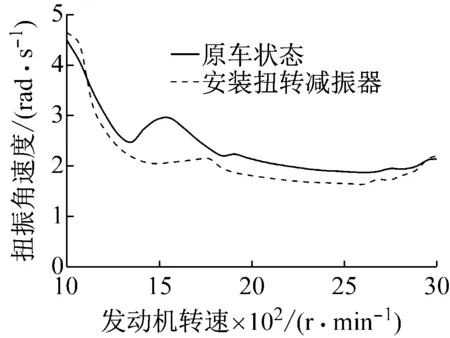
圖7 動(dòng)力傳動(dòng)系扭振測(cè)試

圖8 車(chē)內(nèi)噪聲測(cè)試

圖9 傳動(dòng)系安裝扭轉(zhuǎn)減振器

4 結(jié) 論

(1) 通過(guò)對(duì)扭轉(zhuǎn)減振器動(dòng)態(tài)等效轉(zhuǎn)動(dòng)慣量分析發(fā)現(xiàn)，扭轉(zhuǎn)減振器減振頻帶特性與局域共振聲子晶體帶隙特性是一致的。

(2) 基于局域共振聲子晶體帶隙理論，提出了扭轉(zhuǎn)減振器減振帶隙的計(jì)算方法，并研究了幾何設(shè)計(jì)參數(shù)與材料設(shè)計(jì)參數(shù)對(duì)扭轉(zhuǎn)減振器帶隙的影響規(guī)律。

(3) 運(yùn)用基于局域共振聲子帶隙的計(jì)算方法設(shè)計(jì)扭轉(zhuǎn)減振器，有效解決了某國(guó)產(chǎn)MPV傳動(dòng)系扭轉(zhuǎn)振動(dòng)引致的車(chē)內(nèi)轟鳴聲問(wèn)題，該方法可用于工程實(shí)際中扭轉(zhuǎn)減振器的研發(fā)與設(shè)計(jì)。

參 考 文 獻(xiàn)

[1] BOZCA M. Torsional vibration model based optimization of gearbox geometric design parameters to reduce rattle noise in an automotive transmission[J]. Mechanism and Machine T`heory, 2010, 45(11): 1583-1598.

[2] 吳昱東，李人憲，丁渭平，等. 基于半軸扭轉(zhuǎn)剛度調(diào)校的新型微客轟鳴聲治理[J]. 噪聲與振動(dòng)控制, 2016,36(1): 70-74.

WU Yudong, LI Renxian, DING Weiping, et al. Interior booming noise reduction in new minivans based on axle-shaft torsional stiffness modification[J]. Noise and Vibration Control, 2016,36(1): 70-74.

[3] FOULARD S, RINDERKNECHT S, ICHCHOU M, et al. Automotive drivetrain model for transmission damage prediction[J]. Mechatronics, 2015, 30: 27-54.

[4] DEUSZKIEWICZ P, PANKIEWICZ J, DZIURD J, et al. Modeling of powertrain system dynamic behavior with torsional vibration damper[J]. Advanced Materials Research, 2014, 1036:586-591.

[5] 上官文斌，魏玉明，趙旭，等. 橡膠阻尼式扭轉(zhuǎn)減振器固有頻率計(jì)算與測(cè)試方法的研究[J]. 振動(dòng)工程學(xué)報(bào), 2015,28(4): 550-559.

SHANGGUAN Wenbin, WEI Yuming, ZHAO Xu, et al. A study on method of calculation and measurement for natural frequency of torsional vibration rubber dampers[J]. Journal of Vibration Engineering, 2015,28(4): 550-559.

[6] MENDES A S, MEIRELLES P S, ZAMPIERI D E. Analysis of torsional vibration in internal combustion engines: modelling and experimental validation[J]. Proceedings of the Institution of Mechanical Engineers Part K Journal of Multi-body Dynamics, 2008, 222(2): 155-178.

[7] LIU Z, ZHANG X, MAO Y, et al. Locally resonant sonic materials[J]. Science, 2000, 289: 1734.

[8] ZHANG S, WU J, HU Z. Low-frequency locally resonant band-gaps in phononic crystal plates with periodic spiral resonators[J]. Journal of Applied Physics, 2013, 113(16): 163511-163518.

[9] MEI J, MA G, YANG M, et al. Dark acoustic metamaterials as super absorbers for low-frequency sound[J]. Nature Communications, 2012, 3(2): 132-136.

[10] LU M, FENG L, CHEN Y. Phononic crystals and acoustic metamaterials[J]. Materials Today, 2009, 12(12): 34-42.

[11] ROMERO-GARCA V, KRYNKIN A, GARCIA-RAFFI L M, et al. Multi-resonant scatterers in sonic crystals: locally multi-resonant acoustic metamaterial[J]. Journal of Sound and Vibration, 2013, 332(1): 184-198.

[12] LUCKLUM R. Phononic crystals and metamaterials-promising new sensor platforms[J]. Procedia Engineering, 2014, 87: 40-45.

[13] LI E, HE Z C, WANG G. An exact solution to compute the band gap in phononic crystals[J]. Computational Materials Science, 2016, 122: 72-85.

[14] LI S, CHEN T, WANG X, et al. Expansion of lower-frequency locally resonant band gaps using a double-sided stubbed composite phononic crystals plate with composite stubs[J]. Physics Letters A, 2016, 380(25/26): 2167-2172.

[15] QIAN D, SHI Z. Bandgap properties in locally resonant phononic crystal double panel structures with periodically attached spring-mass resonators[J]. Physics Letters A, 2016, 380(41): 3319-3325.

[16] 溫熙森. 聲子晶體[M]. 北京：國(guó)防工業(yè)出版社, 2009.

[17] SHEN L, WU J, ZHANG S, et al. Low-frequency vibration energy harvesting using a locally resonant phononic crystal plate with spiral beams[J]. Modern Physics Letters B， 2015, 29(1): 1450511-1450529.