考慮旋轉自由度的渦激振動數值模擬研究

康 莊， 倪問池

(哈爾濱工程大學 船舶工程學院， 哈爾濱 150001)

渦激振動現象在海洋工程中廣泛存在，對渦激振動研究已成為研究的熱點之一。在海洋工程中，柱形結構被廣泛采用，且質量比都較低[1]。因此，對渦激振動的研究大多集中在低質量比圓柱結構上。

Khalak等[2]對彈性固定的圓柱結構進行了模型實驗研究，發現當圓柱質量阻尼比較高時，渦激振動響應存在兩個分支，分別對應于初始分支與下端分支，而當質量阻尼比較低時，渦激振動響應存在三個分支，分別對應于初始分支、上端分支和下端分支。Jauvtis等[3]還對m*=2.6的低質量阻尼比圓柱進行了雙自由度渦激振動實驗研究，發現在加速工況中，圓柱橫向最大振幅可達1.5D左右，并且存在回滯現象。此外，還將圓柱渦激振動的尾渦形式總結為2S、2P、2T和2C模式。Khalak等[4]通過對雙自由度圓柱的實驗研究指出，當質量比較大時，圓柱共振頻率將約等于固有頻率。而當質量比較小時，圓柱共振頻率將會略大于固有頻率。進一步，Govardhan等[5]發現，當質量比小于0.54時，圓柱渦激振動響應的下端分支將會缺失。

根據現有的研究成果，當前渦激振動的研究對象主要為單自由度或雙自由度彈性固定的圓柱，對于增加了旋轉自由度的渦激振動，主要的研究形式為人為對結構物施加固定的旋轉角速度，分析流場的特性。

Naik等[6]對雷諾數等于100，不同旋轉角速度下的橢圓結構的流場特性進行了數值模擬研究，發現了旋轉運動對流場特征產生了顯著影響。在旋轉效應下，尾渦模式發現了變化，觀察到了“盤漩渦”以及多頻現象。Lam[7]對旋轉圓柱尾流場進行了實驗研究，并發現當圓柱無量綱旋轉角速度小于1.9時，圓柱的渦泄模式與固定圓柱類似，但隨著旋轉速度的增加，圓柱的渦泄模式會發生顯著變化，并且偏向一邊。

已有文獻表明，當前，在對旋轉結構尾流場的研究中，已經發現了一些新穎的現象。然而這些研究中，結構都是在人為作用下發生旋轉，對于結構在渦致力作用下發生的旋轉，已有的研究并不多。

Wilde[8]對自由站立式立管進行了渦激運動模型試驗，發現在一定的來流速度下，浮筒會產生艏搖運動。李鵬[9]在對浮力筒的六自由度渦激運動實驗中也發現了艏搖現象。

渦激振動的艏搖現象已經在浮力筒的實驗與工程實際中被發現。這表明尾渦的周期性脫落，還會產生周期性的力矩，對于浮力筒這類系泊結構，將會造成艏搖現象，對于彈性或剛性固定的立管，則會造成周期性的扭矩，這將大大降低結構的疲勞壽命，甚至有可能使結構發生扭轉變形。然而，當前對于該現象缺乏詳細的分析。本文基于本文基于OpenFoam軟件，對考慮旋轉自由度下的低質量比圓柱渦激振動響應特性進行數值模擬研究。首先，參照Jauvtis等的實驗，對雙自由度低質量比圓柱進行數值模擬，然后在相同的邊界條件下，對圓柱增加旋轉自由度，進行數值模擬，并對兩種自由度下渦激振動響應進行對比分析。

1 數值方法

1.1 湍流模型

本文數值模擬中，流體采用的是雷諾平均控制方程，其表達式為

(1)

(2)

式中：u,p為時均速度與壓力；μ為動力黏度；ρ為流體密度。

為了對上述控制方程進行封閉，結合了k-ω與k-ε湍流模型優勢的SST模型[10]被應用于本次數值模擬中。SST模型具有較高計算精度以及穩定性，在工程中被廣泛應用。其無量綱的形式如下

渦黏性

(3)

湍動能

(4)

比耗散率

(5)

第二混合函數

(6)

湍動能k的生成項

(7)

第一混合函數

(8)

其中，

(9)

F1在近壁面處取1，在遠壁面處取值為0，實現了在近壁面處采用k-ω模型，在遠壁面處使用k-ε模型。相應地，輸運方程中的系數可表示為

φ=φ1F1+φ2(1-F1)

(10)

SST模型中，各系數的取值如表1所示。

表1 SST湍流模型系數

固體可簡化為質量-彈簧-阻尼系統，其運動的控制方程可表示為

Mx″(t)+Kxx(t)+Cxx′(t)=Fx(t)

My″(t)+Kyy(t)+Cyy′(t)=Fy(t)

式中：M為圓柱質量；K和C分別為彈簧剛度和阻尼系數；x(t)、y(t)與θ(t)分別為順流向位移、橫流向位移以及轉角位移；F為流體力；Iθ為圓柱對瞬心的轉動慣量；r為位置矢量。

1.2 計算域及網格

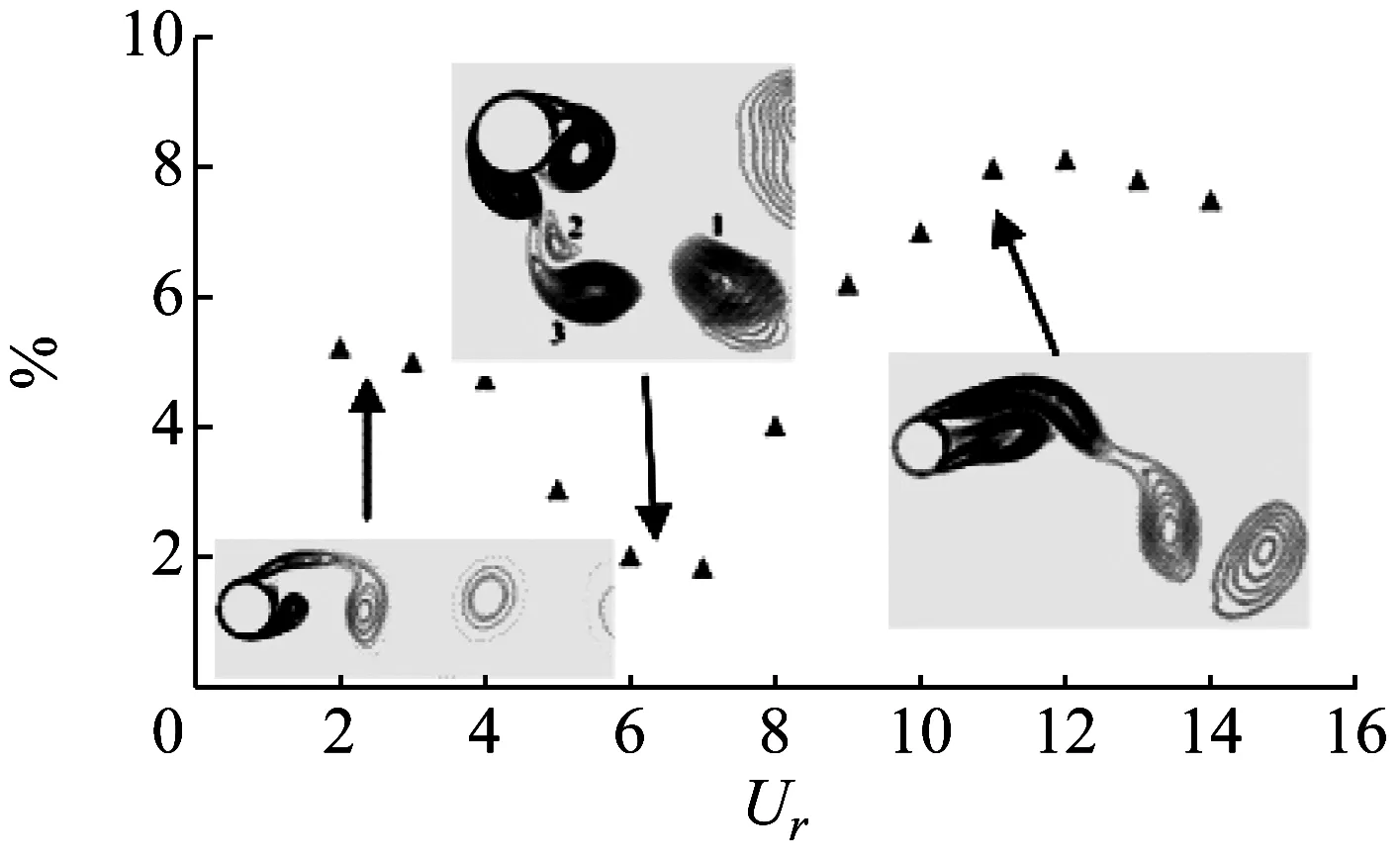
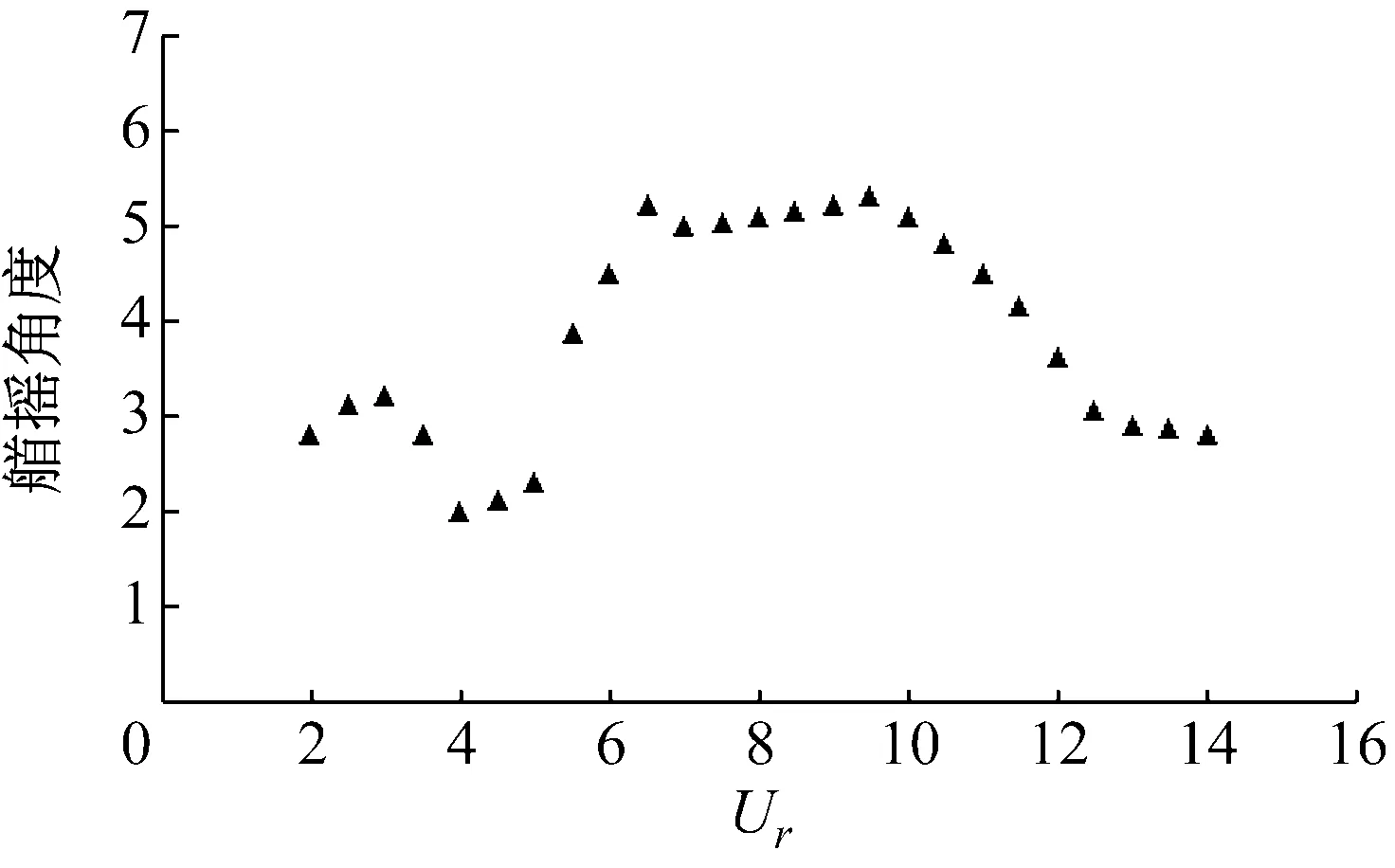
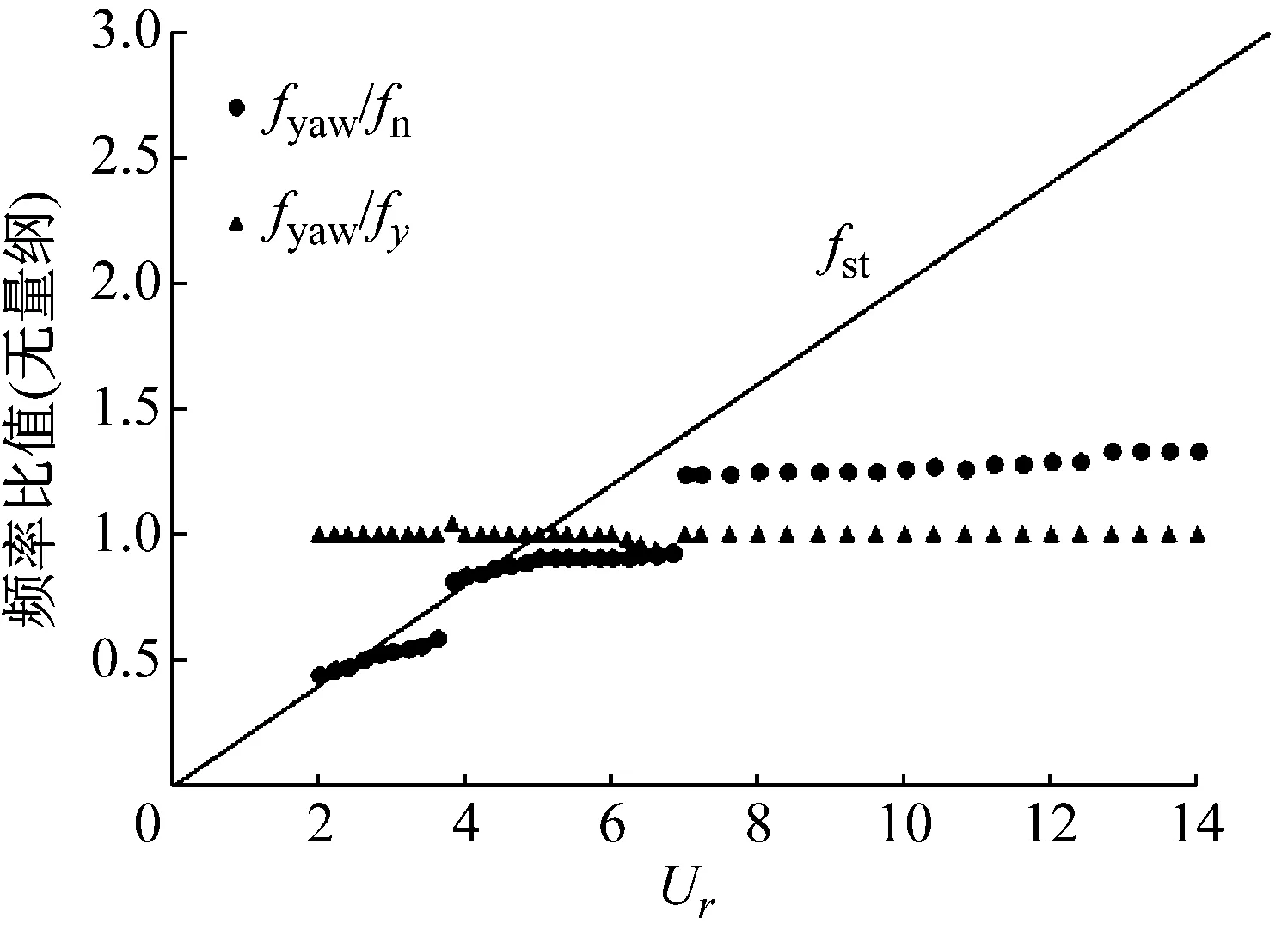
本次數值模中，圓柱參數參照Jauvtis等的實驗設定參數，具體參數為：直徑D=0.038 1 m，質量比m*=2.6,質量阻尼比m*ξ=0.013，靜水中振動固有頻率fn=0.4。流場的網格劃分如圖1所示。考慮到圓柱振動區域以及尾渦的影響范圍，總體計算域范圍取為：-12D

時間步長根據庫朗數(Cn)確定[12]。庫朗數的表達形式為

(11)

式中：u為流速；Δt為時間步長；Δx為網格尺寸。在不同工況中，時間步長根據流速作相應調整，使得計算過程中庫朗數最大值為0.2左右。

圖1 計算域整體網格

本文采用的網格以及數值模擬方法與文獻[13]一致。文獻[13]的計算結果表明，該網格及數值模擬方法對該工況下雙自由度渦激振動的計算具有較高的精度。考慮到增加旋轉自由度后，流場特征并未發生顯著變化，因此，該網格對于增加旋轉自由度后的渦激振動數值模擬仍然具有較高的正確性。

1.3 旋轉自由度的設定

本文數值模擬中，對渦激振動艏搖現象的考察，通過對相應的OpenFoam限制文件中，增加圓柱的旋轉自由度實現。運用后處理軟件，對圓柱渦激振動穩定階段數值模擬結果進行分析，可提取旋轉角速度時歷數據，圓柱的艏搖角度可通過對角速度進行積分求得。此外，圓柱的旋轉阻尼設為0。

2 計算結果及分析

2.1 計算工況

根據Khalak等的實驗結果，渦激振動響應在流場加速、勻速以及減速工況下會呈現出不同的響應。本文僅分析流場加速的工況，即流速從0勻速增加到目標值，然后保持勻速。

運用上述網格，分別計算穩定階段流場約化速度范圍從0～14，雙自由度，以及增加旋轉自由度的渦激振動響應，并進行對比。

2.2 振幅響應對比

兩種自由度下，渦激振動隨約化速度的橫向及順流向最大振幅響應如圖2和圖3所示。此外，Jauvtis等的實驗結果也繪于圖中作為參照。

圖2 不同約化速度下橫向最大振幅響應

圖3 不同約化速度下順流向最大振幅響應

如圖所示，橫流向以及順流向的數值模擬的結果均成功捕捉到三個響應分支，分別為初始分支，上端分支與下端分支。上端分支與下端分支的跳躍點在約化速度Ur=7附近。數值模擬的結果與實驗結果基本吻合，除了數值模擬響應的上端分支與下端分支的跳躍點略微向左偏移。在林琳等[14-16]的文章中也出現了類似的現象，這也許是實際實驗過程中三維效應或者其他干擾因素造成的。

此外，還可以發現，無論是橫流向還是順流向，增加了旋轉自由度的渦激振動振幅響應與雙自由度渦激振動振幅響應具有相同的趨勢，且振動幅值較為接近，但還是可以觀察到，增加了旋轉自由度后，渦激振動最大橫向振幅響應幅值小于雙自由度渦激振動幅值。根據機械能守恒原理，增加了旋轉自由度后，有一部分振動的機械能轉換為旋轉機械能，使得最大振幅有所減小。

為了更直觀地體現兩種自由度下，渦激振動振幅響應差異，將兩種自由度工況的振幅差異繪于圖4中。其中，橫坐標代表穩定階段的約化速度，縱坐標代表最大振幅差異，用百分比表示(增加旋轉自由度后最大振幅減小的百分比)。考慮到順流向的振幅較小，工程中主要關心的是橫流向的振動，并且橫流向與縱流向的振幅響應變化趨勢基本一致，因此本文僅對橫向振動進行分析。

圖4 增加旋轉自由度后振幅減小比例

從圖4中可以看出，兩種自由度工況的振幅差異隨著流速的變化，也呈現出三段分支，且三段分支對應的流速區間與振幅響應的分支區間基本一致。在此，為了便于對照，將振幅差異圖中的分支也稱為“初始分支”、“上端分支”與“下端分支”。在上端分支中，振幅的減小比例約為5%，在上端分支中，振幅的減小比例約為2%，而在下端分支中，減小比例達到了8%左右。

根據機械能守恒原理，在下端分支中，轉換為旋轉機械能所占的比例最大，而在上端分支中，比例最小。這顯然與各分支中的流場特性密切相關。為了分析其機理，將各分支中的尾渦模式也繪于圖4中。

在初始分支中，尾渦的模式為“2S模式”，即在每個周期內，兩個獨立的，旋轉方向相反的尾渦均勻形成并從物體后方交替脫落。此時，圓柱上下側交替產生均勻的壓力差，在壓力差的作用下，圓柱產生位移，并出現艏搖現象。在上端分支中，尾渦模式為“2T模式[17]”，此時，物體后方每個周期發放出兩個渦對，每個渦對包含三個渦，并且三個渦的旋轉方向不完全相同。在“2T模式”中，上下側存在渦同時脫落的情況，此時上下側壓力差存在部分抵消的情況，轉化為旋轉機械能的比例也有所降低。在下端分支中，尾渦模式為“2P模式”，在每個周期內，物體后方發放出兩個渦對，并且渦對中的兩個漩渦旋轉方向相反。該尾渦模式的上下側壓力變化情況與“2S模式”類似，交替產生均勻的壓力差，但由于每次發放出兩個渦對，相對壓力差較大。此時，轉化為旋轉機械能的比例也有所增加。由此可以斷定，艏搖運動是上下側壓力差造成的。

2.3 頻率響應對比

兩種自由度下，渦激振動頻率響應隨約化速度的變化趨勢如圖5所示。

圖5 不同約化速度下橫向振動頻率響應

在圓柱渦激振動頻率響應中，也可以觀察到明顯的三段分支，分別對應于初始分支、上端分支以及下端分支。在初始分支中，振動頻率隨著速度的增大而增大，并且接近fst，但比fst略小。在上端分支中，fy/fn約為0.9，即橫向振動頻率鎖定于系統固有頻率。而在下端分支中，仍然可以觀察到鎖定現象，但此時fy的頻率不再等于固有頻率，fy/fn的值穩定在1.25左右。數值模擬結果與實驗結果基本吻合。

此外，還可以發現，兩種自由度工況下，圓柱渦激振動頻率響應結果完全重合。因此可以得出，增加旋轉自由度不會改變圓柱振動頻率。

2.4 艏搖響應分析

下面單獨考察增加了旋轉自由度的圓柱渦激振動數值模擬結果，提取圓柱的最大旋轉角度，分析其艏搖響應特性。各約化速度下，圓柱艏搖幅度如圖6所示。其中，橫坐標表示流場約化速度，縱坐標表示艏搖幅值，在圖中用角度表示。

從圖6中可以看出，隨著流場速度的增加，艏搖幅值經歷了“增加→減小→增加→穩定→減小”的過程。當Ur=2～3時，艏搖幅值隨速度增加而增大，最大可達3.2度左右。當Ur=3～4時，艏搖幅值迅速減小，并達到最小值2度左右。隨后，艏搖幅度隨約化速度增大而增大，當Ur=6時，艏搖幅值達到最大值，5.2度左右，隨后在Ur=6～10內，艏搖幅值基本保持恒定。當約化速度大于10后，艏搖幅值開始減小。

此外，如圖4所示，當約化速度等于10左右時，振幅衰減量遠大于約化速度為6時的值，即總機械能中，轉化為旋轉機械能的比例遠比約化速度為6時大。但Ur=10時的艏搖幅值仍然小于Ur=6時的幅值。總體上看，艏搖幅值的變化趨勢與圖2所示的振幅隨約化速度的變化趨勢基本一致，仍然呈現出三個分支，但上端分支與下端分支之間的跳躍沒有振幅響應這么明顯。由此可以得出，渦激振動艏搖運動幅值大小主要取決于振動的劇烈程度，即系統總機械能的大小，但也會受到尾渦形態等流場特性的影響。

圖6 不同約化速度下艏搖幅值響應

艏搖運動的頻率響應如圖7所示。其中，fyaw/fn表示艏搖頻率與固有頻率的比值，fyaw/fy表示艏搖頻率與橫向振動頻率的比值。特別需要說明的是，當艏搖運動出現多個主頻率時，取最大的頻率分量。

圖7 不同約化速度下艏搖頻率響應

從圖7中可以看出，艏搖運動的頻率響應也存在明顯的三個分支。從fyaw/fy的響應曲線可以看出，艏搖頻率與圓柱渦激振動橫向振動頻率基本相等，除了在每段分支之間的過渡階段存在略微偏差。這也許是由于在過渡階段中，頻率較為雜亂，頻率分析較為困難，存在一定的誤差。因此，從頻率分析中可以得出，圓柱渦激振動引起的艏搖頻率與橫向振動頻率一致，可以推斷出，兩者具有相同的激勵源，即艏搖運動也是由于漩渦交替脫落引起的壓力差造成的。

3 結 論

本文基于OpenFoam軟件，采用數值模擬方法對對考慮旋轉自由度的低質量比圓柱渦激振動響應特性進行了數值模擬研究，可以得出以下結論：

(1) 當具有旋轉自由度時，圓柱在渦激振動過程中，會出現艏搖現象。

(2) 圓柱產生艏搖運動的原因是部分振動機械能轉化為旋轉機械能，因此，艏搖運動的產生會使圓柱渦激振動的幅值略微降低，且能量的轉化比例與尾渦特征密切相關。

(3) 艏搖運動的出現，不會改變圓柱渦激振動的振動頻率。

(4) 艏搖運動幅值的變化趨勢與橫向振幅的變化趨勢類似，且大小主要取決于振動的劇烈程度，即系統總機械能的大小，但也會受到尾渦形態等流場特性的影響。

(5) 圓柱艏搖頻率與橫向振動頻率一致，可以推斷出，兩者具有相同的激勵源，即艏搖運動也是由于漩渦交替脫落引起的壓力差造成的。

參 考 文 獻

[1] KANG Zhuang, NI Wenchi, SUN Liping. An experimental investigation of two-degrees-of-freedom VIV trajectories of a cylinder at different scales and natural frequency ratios[J]. Ocean Engineering,2016,126:187-202.

[2] KHALAK A, WILLIAMSON C H K. Dynamics of a hydro elastic cylinder with very low mass and damping[J]. Journal of Fluids and Structures, 1996, 10(5): 455-472.

[3] JAUVTIS N, WILLIAMSON C H K. The effect of two degrees of freedom on vortex-induced vibration at low mass and damping[J]. Journal of Fluid Mechanics, 2004, 509(509):23-62.

[4] KHALAK A, WILLIAMSON C H K. Motions, forces and mode transitions in vortex-vibrations at lowmass-damping[J]. Journal of Fluids and Structures, 1999, 13: 813-851.

[5] GOVARDHAN R N, WILLIAMSON C H K. Vortex-induced vibrations of a sphere[J]. Journal of Fluid Mechanics, 2005, 531(531):11-47.

[6] NAIK S N, VENGADESAN S, PRAKASH K A. Numerical study of fluid flow past a rotating elliptic cylinder[J]. Journal of Fluids & Structures, 2017, 68:15-31.

[7] LAM K M. Vortex shedding flow behind a slowly rotating circular cylinder[J]. Journal of Fluids & Structures, 2009, 25(2):245-262.

[8] WILDE J D. Model tests on the vortex induced motions of the air can of a free standing riser system in current[C]∥ Proceedings of the Deep Offshore Technology Conference. Stavanger：DOTC， 2007.

[9] 李鵬. 浮力筒自由渦激運動試驗研究[D]. 哈爾濱:哈爾濱工程大學, 2015.

[10] MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. Aiaa Journal, 2012, 32(8):1598-1605.

[11] CLOETE S, JOHANSEN S T, AMINI S. Grid independence behaviour of fluidized bed reactor simulations using the two fluid model: detailed parametric study[J]. Powder Technology, 2015, 289:65-70.

[12] MORAGUES GINARD M, BERNARDINO G, VZQUEZ M, et al. Fourier stability analysis and local courant number of the preconditioned variational multiscale stabilization (P-VMS) for euler compressible flow[J]. Computer Methods in Applied Mechanics & Engineering, 2015, 301:28-51.

[13] KANG Z, NI W, SUN L. A numerical investigation on capturing the maximum transverse amplitude in vortex induced vibration for low mass ratio[J]. Marine Structures, 2017, 52:94-107.

[14] 林琳, 王言英. 不同湍流模型下圓柱渦激振動的計算比較[J]. 船舶力學, 2013,17(10):1115-1125.

LIN Lin, WANG Yanying. Comparison between different turbulence models on vortex induced vibration of circular cylinder[J]. Journal of Ship Mechanics, 2013, 17(10):1115-1125.

[15] 谷家揚, 楊建民, 肖龍飛. 兩種典型立柱截面渦激運動的分析研究[J]. 船舶力學, 2014，18(10):1184-1194.

GU Jiayang, YANG Jianmin, XIAO Longfei. Study on vortex induced motion of two typical different cross-section columns[J]. Journal of Ship Mechanics, 2014,18(10):1184-1194.

[16] PAN Z Y, CUI W C, MIAO Q M. Numerical simulation of vortex-induced vibration of a circular cylinder at low mass-damping using RANS code[J]. Journal of Fluids & Structures, 2007, 23(1):23-37.

[17] WILLIAMSON C. A high-amplitude 2T mode of vortex-induced vibration for a light body in XY motion[J]. European Journal of Mechanics-B/Fluids, 2004, 23(1):107-114.