基于迭代濾波和快速峭度圖的滾動軸承微弱故障特征提取

鐘先友， 田紅亮， 趙春華， 陳保家， 陳法法

(三峽大學 水電機械設備設計與維護湖北省重點實驗室， 湖北 宜昌 443002)

滾動軸承的故障診斷對于減少經濟損失和避免人員傷亡具有十分重要的意義。Huang等[1]提出了一種自適應的時頻分析方法—經驗模式分解(Empirical Mode Decomposition，EMD)。EMD方法能將一個非穩非線性信號分解為一系列本征模態函數，在滾動軸承故障中已經取得了一定的應用[2-3]。唐海英等[4]將階次跟蹤和經驗模態分解相結合對滾動軸承信號進行包絡解調分析。Cheng等[5-6]將經驗模態分解分別與能量算子解調和邊際譜相結合對滾動軸承進行診斷，唐先廣等[7]將基于獨立分量分析與希爾伯特-黃變換用于軸承故障特征提取，蘇文勝等[8]對滾動軸承信號進行經驗模態分解，選取前兩個分量重構，再利用譜峭度法選取最佳帶通濾波器參數進行帶通濾波，最后進行包絡解調來提取故障特征，論文中確定重構的模式分量是依靠經驗來確定，且論文研究表明，譜峭度對信號中的噪聲敏感，噪聲影響譜峭度法選取最佳帶通濾波器參數，進而影響包絡解調的效果。應用包絡譜分析，帶通濾波參數的選擇仍然是一個難點，濾波參數的選擇對信號分析結果影響很大[9]。陳略等[10-11]將總體平均經驗模態分解用于對滾動軸承進行診斷，取得了較好的效果。

EMD存在過包絡、欠包絡、模態混淆、端點效應等問題[12-13]。Lin等介紹了一種自適應信號分析方法—迭代濾波，迭代濾波方法能自適應地將一個復雜的多分量信號分解為若干個瞬時頻率具有物理意義的內稟模態分量之和。

滾動軸承發生故障時產生的周期性沖擊引起軸承系統的高頻固有振動，故障特征被調制到高頻段，故障信息主要集中在高頻段，采用迭代濾波方法將軸承振動信號分解為若干個內稟模態分量，最先分解得到的內稟模態分量包含了最重要的高頻成分，對其采用快速峭度圖[14]構造最優帶通濾波器，最后將濾波后信號的包絡譜與軸承故障特征頻率進行比較，可以診斷出軸承的具體故障。

1 迭代濾波基本原理

迭代濾波方法能夠自適應地將一個復雜信號分解為若干個相互獨立的內稟模態分量和一個趨勢項之和。對于X(t)，t∈R，定義L為信號X(t)的基線提取算子，用來獲得信號的移動均值，代表信號中的局部相對低頻成分，定義τ獲得信號X(t)的波動值，代表信號中的局部相對低頻成分。

τ(X)=X-L(X)

(1)

分解過程中，迭代濾波分解類似經驗模態分解中的篩分分解過程，在迭代濾波分解的篩分分解過程中，用移動均值代替經驗模態分解過程中的上下包絡線均值，通過下式求得第一個內稟模態分量

(2)

式中:τn為運用算子τ對信號X進行n次篩分變換，直到信號中的極值點和過零點數目必須相等或至多相差一個，從而得到第一個內稟模態分量I1，將I1從原信號中提取出來，得到一個新的剩余信號，將剩余信號視為原始數據，重復上述步驟。直到剩余信號為一個單調或常函數。信號迭代濾波分解結束后，把原始信號X分解成若干個從高到低不同頻率段的內稟模態分量Ik和一個單調趨勢分量r(t)之和。信號迭代濾波分解的整個過程可以表示為

(3)

(4)

式中:m為內稟模態分量個數，為了保證被分離出來的內稟模態函數有意義，定義篩分的停止準則，采用標準差法，設

(5)

(6)

式中：SD為篩分門限值，在計算過程中一般取0.001～0.2，如果SD小于這個門限值，篩分過程就停止。

對于迭代濾波分解，文獻[15]中采用的是雙平均低通濾波器，窗長為N的雙平均濾波器L通過卷積生成信號X的移動均值

(7)

2 仿真信號分析

考察式(8)所示仿真信號

x(t)=x1(t)+x2(t) =

[1+0.5sin(5πt)]·cos(250πt+20cos πt2)+

5sin(40πt)t∈[0,1]

(8)

式中：x1(t)為調頻-調幅信號；x2(t)為正弦信號。信號x(t)的時域波形如圖1所示。在不處理端點的情況下，對x(t)進行經驗模態分解，經過8次迭代后得到第一個分量C1，它對應信號x(t)中的載頻為125 Hz的調幅-調頻分量，將C1從x(t)中分離出來，對剩余信號再作4次迭代后得到第二個分量C2，它對應信號x(t)中的頻率為20 Hz的正弦分量，分別如圖2所示。

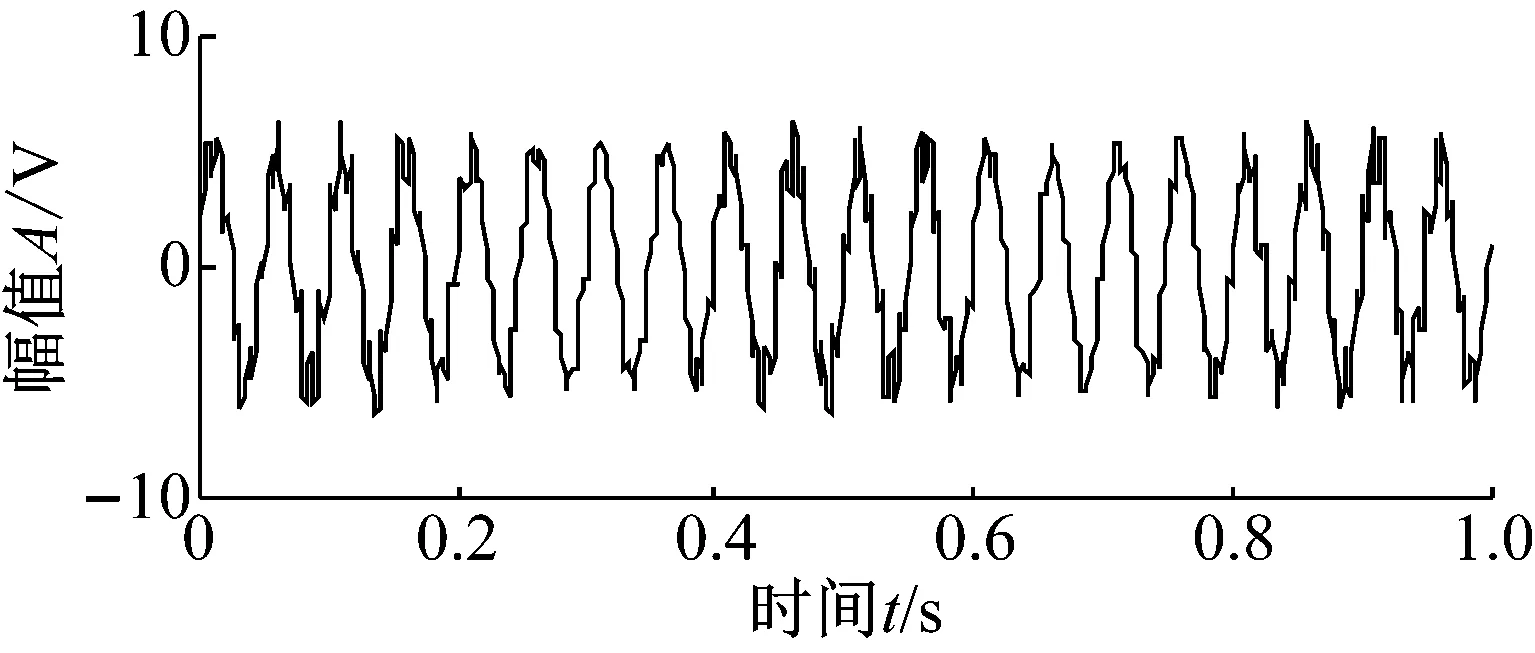
圖1 仿真信號的時域波形

在不處理端點的情況下，對x(t)進行迭代濾波分解，經過4次迭代后得到第一個分量I1，它對應信號x(t)中的載頻為125 Hz的調幅-調頻分量，將I1從x(t)中分離出來，對剩余信號再作2次迭代后得到第二個分量I2，它對應信號x(t)中的頻率為20 Hz的正弦分量，它們的幅值與信號中相應成分也有嚴格的對應關系，分別如圖3所示，從圖中可以看出，各分量幾乎沒有產生端點效應現象。從以上分析可知，迭代濾波分解方法對兩個分量的分解取得了較好的效果。經驗模態分解得到一個分量要的迭代次數明顯要比迭代濾波分解多。

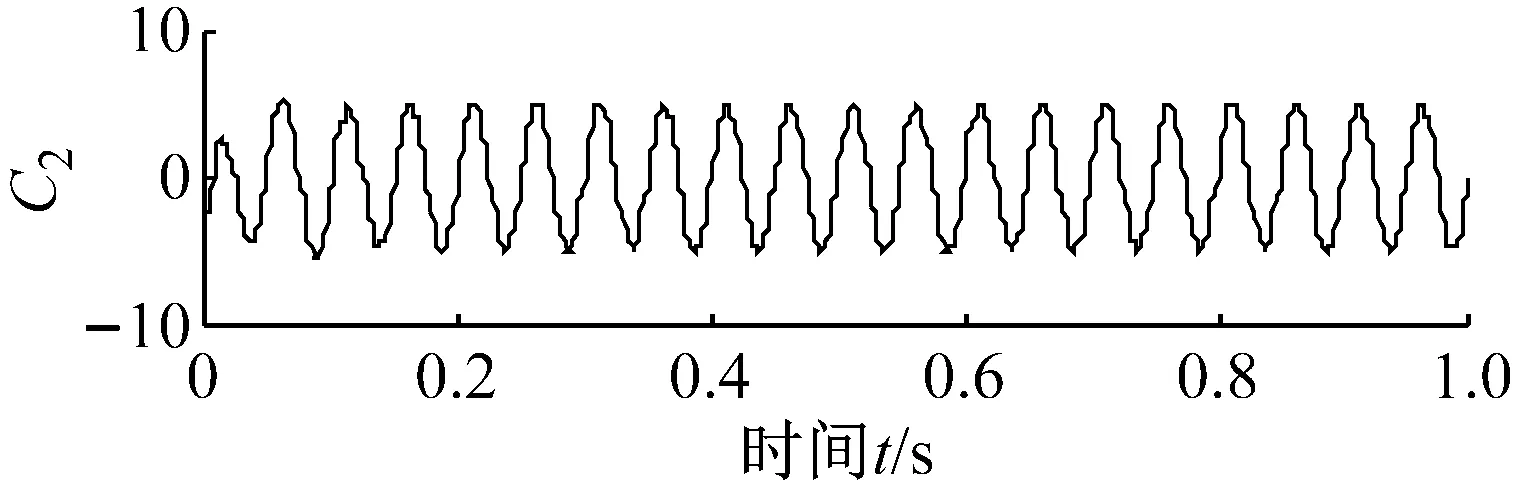
圖2 EMD方法分解結果

對比圖2和圖3可以看出，迭代濾波和經驗模態分解方法都存在著端點效應，經驗模態分解產生的端點效應要比迭代濾波分解明顯。

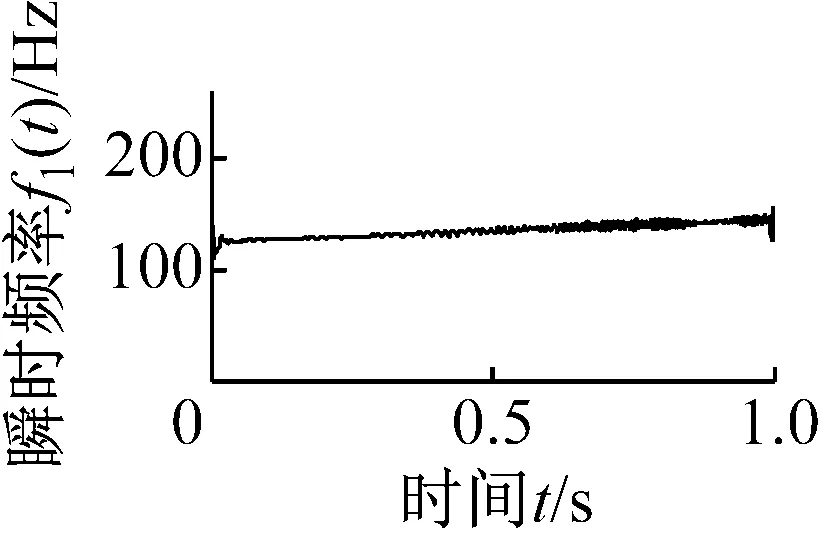
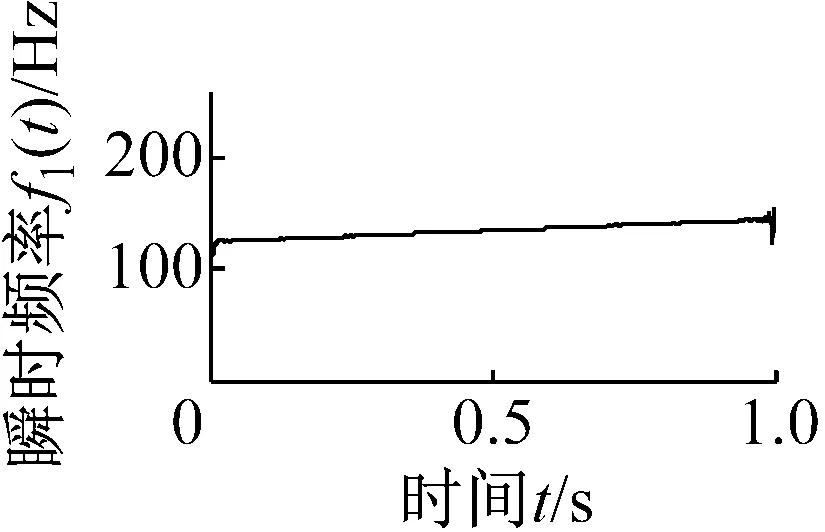
分別對圖2和圖3所示的兩個分量進行Hilbert變換求它們的瞬時幅值與瞬時頻率，分別如圖4和圖5所示，從圖4中可以看出，由于Hilbert變換的邊緣效應，分量C1和C2的瞬時幅值與瞬時頻率部分失真，而分量I1和I2的瞬時幅值與瞬時頻率較好地提取出原信號的真實信息。因此在未處理端點情況下，迭代濾波方法優于經驗模態分解方法。

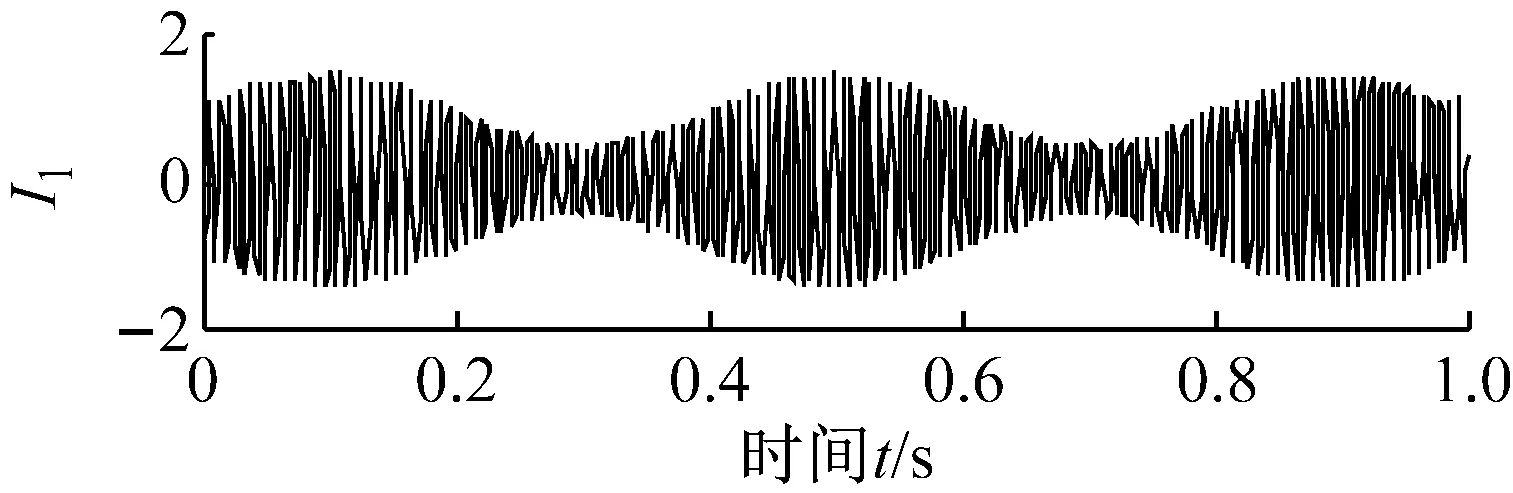
圖3 迭代濾波方法分解結果

3 基于IF和快速峭度圖的軸承診斷方法流程

將迭代濾波分解和快速峭度圖相結合應用于滾動軸承故障診斷中，主要包括以下步驟：

步驟1用迭代濾波分解對信號x(t)進行分解，得到若干個I1,I2，…，In分量；

步驟2對第一個高頻分量求快速峭度圖，確定濾波的中心頻率和帶寬并對信號進行帶通濾波求平方包絡譜；

步驟3進行平方包絡譜分析并與故障特征頻率進行比較，從而確定軸承故障狀態。

4 軸承故障仿真信號分析

為了驗證本文所提出的方法在軸承故障特征提取中的有效性，對軸承故障的仿真信號進行分析。根據文獻[16]建立滾動軸承元件發生單點局部損傷時傳感器所采集到的信號模型為

sin[2πf2(t-kT)]U(t-kT)+n(t)

k=1,2,3,…

(9)

m(t)=A[1+B·cos(2πf1t)]

(10)

式中：m(t)為沖擊幅值，是幅值調制函數；f1為第一調制頻率，等于軸的轉頻或滾動體的公轉頻率；T為故障特征周期；f2為軸承座-傳感器系統的某一固有頻率，即載波頻率；c為沖擊信號衰減指數；U(t)為單位階躍函數；n(t)為噪聲。其中取固有頻率f2為4 kHz，阻尼系數為c=0.1，n(t)=0，T=1/150，m(t)=1。根據式(9)和式(10)得到外圈故障的時域波形如圖6所示。向信號中添加Gauss白噪噪聲，信噪比為-11.3 dB，加噪信號的時域波形如圖7所示。

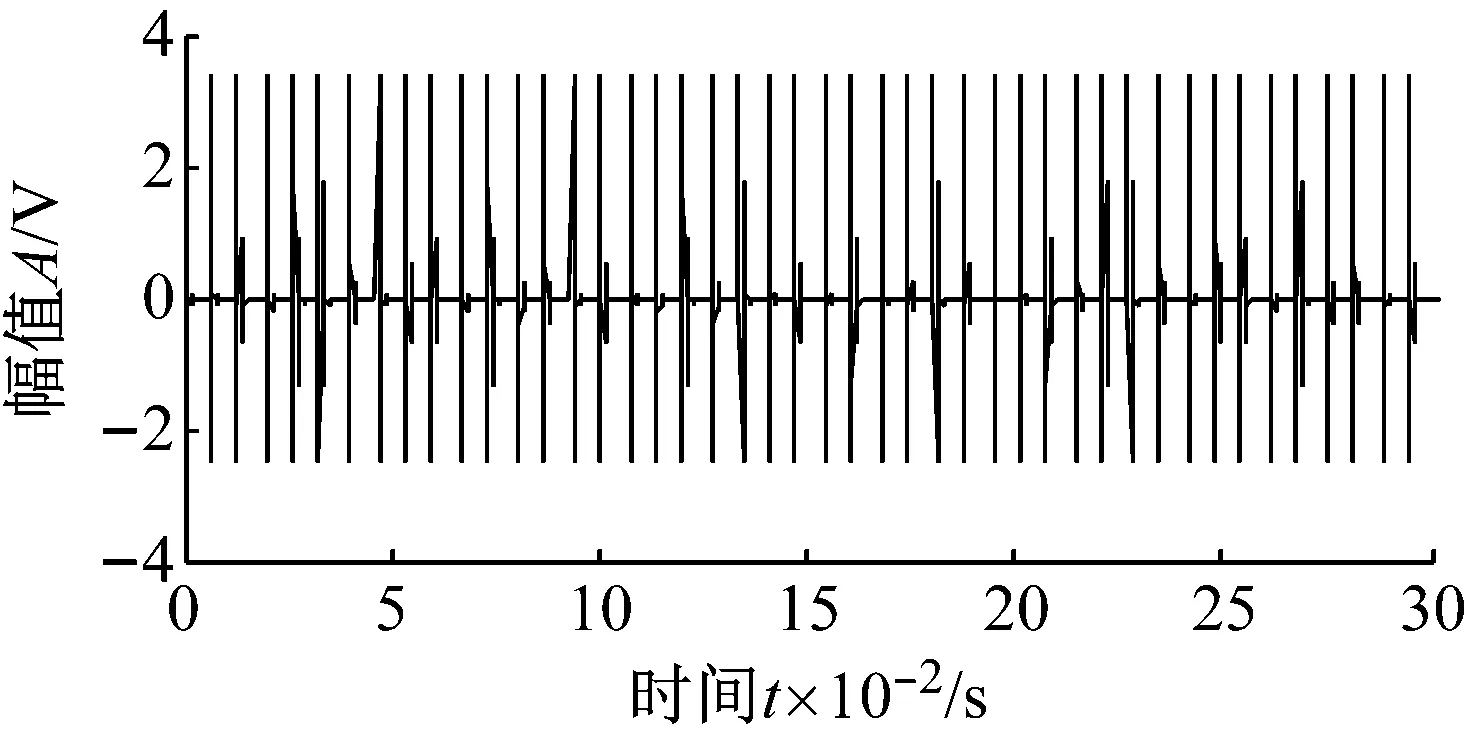
圖6 軸承故障模擬信號的時域波形

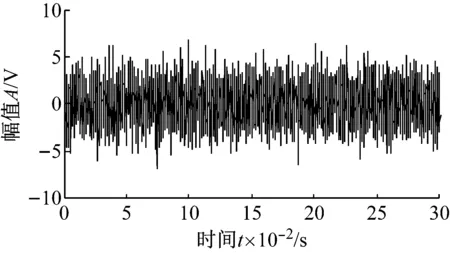
圖7 加噪后軸承故障模擬信號的時域波形

采用迭代濾波方法對該故障仿真信號進行分解，得到8個內稟模態分量和一個殘余分量，前三個分量和原信號的峭度值見表1。

表1 信號與分量的峭度

從表1可見，高頻分量I1的峭度值較原信號增大，說明迭代濾波具有一定的降噪作用。第一個分量I1的快速峭度圖如圖8所示，帶通濾波器的中心頻率為1 250 Hz，帶寬為833.33 Hz，以此參數進行帶通濾波后求分量I1的平方包絡譜如圖9。從圖9中可以清楚地看出，在故障特征的一倍頻(150 Hz)及其倍頻處有明顯的譜線，驗證了基于迭代濾波和快速峭度圖的方法的有效性。

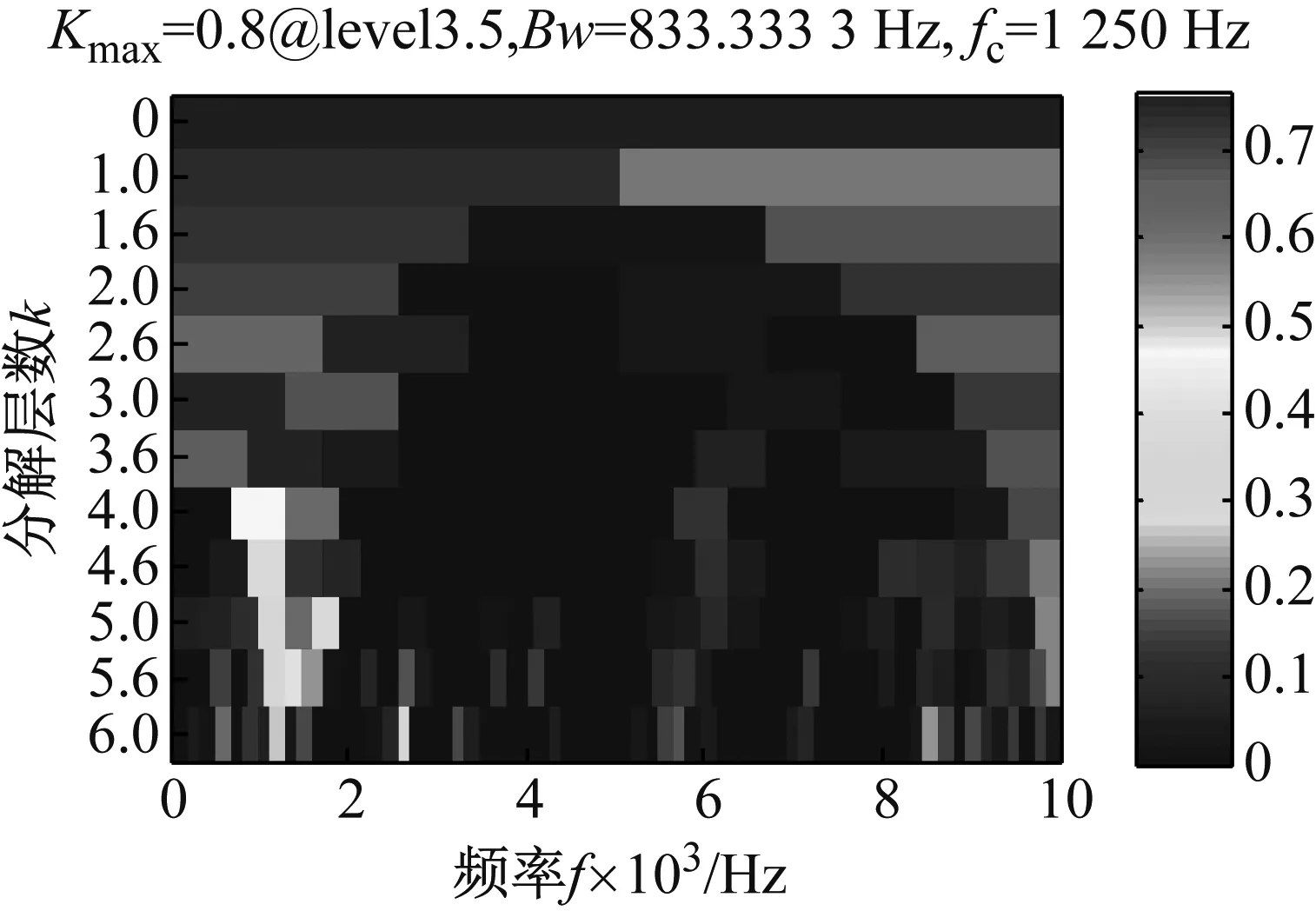
圖8 加噪后軸承故障模擬信號的峭度圖

圖9 濾波后I1分量的平方包絡譜

為了說明迭代濾波的優勢，采用EMD對該故障仿真信號進行分解，前三個分量和原信號的峭度值見表2。對第一個分量進行快速峭度圖分析并進行帶通濾波后求信號的平方包絡譜如圖10。從圖10中可以看出，在故障特征的一倍頻和二倍頻可以識別，但是信噪比低。對比表1和表2以及圖9和圖10，可知迭代濾波比EMD的頻率族分離和降噪能力強，也說明了本文方法的優勢。

5 軸承外圈故障診斷實例

為了真實的模擬早期軸承故障，進行了軸承全生命周期的實驗，即軸承從完好狀態運轉到發生故障，實驗裝置示意圖如圖11所示，試驗臺包括安裝在同一個軸上的4個軸承，軸是由交流電機帶動，轉速控制在2 000 r/min，軸承型號為ZA-2115，雙列滾子軸承，每列滾子數量為16，滾子組節圓直徑為75.5 mm，滾子直徑為8.4 mm，接觸角為15.17°，經計算知軸承外圈故障特征頻率為236.4 Hz。軸承振動數據通過DAQ-6062E數據采集卡每隔10 min采集一次，采樣頻率20 480 Hz。實驗運行6天后停機，發現軸承1出現外圈磨損故障。

表2 信號與分量的峭度

圖10 濾波后軸承信號的平方包絡譜

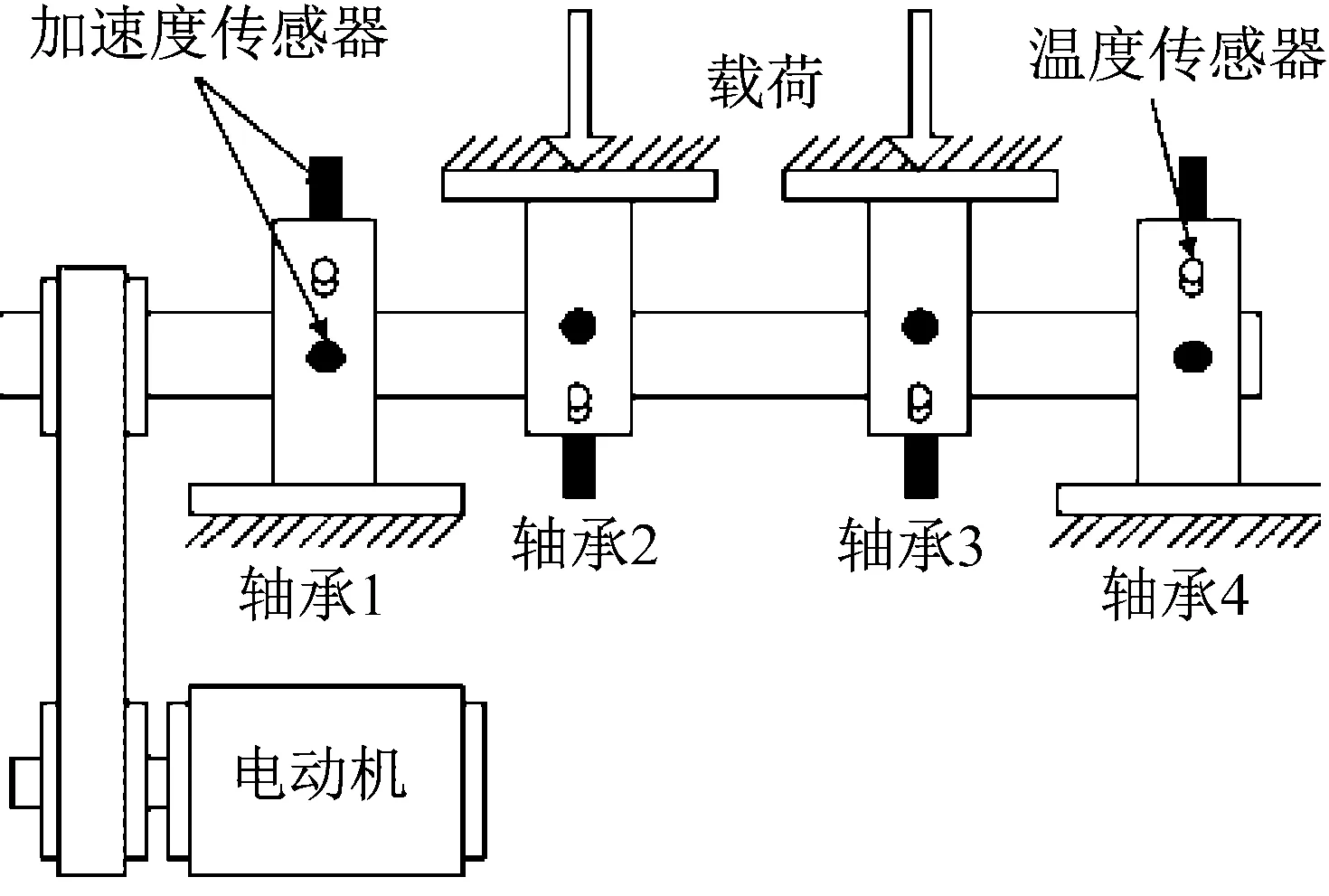
圖11 軸承實驗臺

為了檢驗本文方法提取軸承早期故障的能力，對軸承早期振動信號進行分析。圖12是試驗第二天測得的軸承振動信號的時域波形。對軸承振動信號進行Hilbert變換計算包絡譜，如圖13所示，在外圈故障特征頻率236.4 Hz及其二倍頻附近無突出的譜線，故無法提取出軸承故障的有用信息。

圖12 軸承信號的時域波形

采用EMD對該軸承信號進行分解，對第一個分量進行快速峭度圖分析并進行帶通濾波后求信號的平方包絡譜，如圖14所示。從圖14中可以看出，在故障特征的倍頻處無明顯的譜線，與實際不符。

圖13 軸承信號的包絡譜

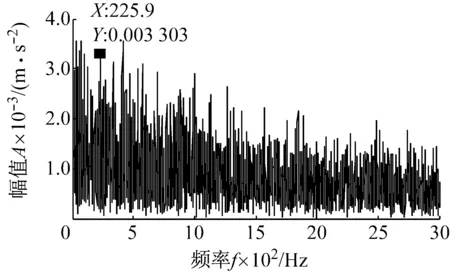
圖14 濾波后軸承信號的平方包絡譜

采用迭代濾波方法對該軸承信號進行分解，得到10個內稟模態分量和一個殘余分量，第一個分量如圖15所示，前三個分量和原信號的峭度值見表3。

表3 信號與分量的峭度

從表3可見，高頻分量I1的峭度值較原信號增大，表明迭代濾波具有一定的降噪作用。第一個分量I1的快速峭度圖如圖16所示，帶通濾波器的中心頻率為5 120 Hz，帶寬為10 240 Hz，以此參數進行帶通濾波后求分量I1的平方包絡譜如圖17。從圖17中可以清楚地看出，在故障特征頻率處有明顯的譜線，可推斷出軸承存在局部故障，與實際相符，從而驗證本文方法的有效性。

圖15 I1分量的時域波形

圖17 濾波后I1分量的平方包絡譜

6 結 論

本文研究了一種新的信號分析方法-迭代濾波方法，并把它引入到軸承故障診斷中，通過仿真信號與軸承故障診斷工程實例的分析驗證了迭代濾波分解和快速峭度圖的診斷方法在軸承故障診斷中的有效性。針對本文所述方法的特點分析如下:

(1) 迭代濾波分解方法是一種新的非平穩信號處理方法，它能將一個多分量信號自適應地分解成若干個分量，迭代濾波分解方法在減少迭代次數和抑制端點效應等方面優于EMD方法。

(2) 采用迭代濾波分解方法對軸承故障信號進行自適應分解濾波，分離出高頻調制信號，可以突出故障信號特征。

(3) 先對信號分解，再對高頻分量進一步進行快速峭度圖分析，能更準確地匹配故障特征，增強滾動軸承故障特征提取的效果。

參 考 文 獻

[1] HUANG N E，SHEN Z，LONG S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London Series，1998，454(1971):903-995.

[2] CHENG Junsheng，YU Dejie，YANG Yu. Application of SVM and SVD technique based on EMD to the fault diagnosis of the rotating machinery[J]. Shock and Vibration，2009，16(1): 89-98.

[3] 湯寶平，蔣永華，張詳春. 基于形態奇異值分解和經驗模態分解的滾動軸承故障特征提取方法[J]. 機械工程學報，2010，46(5)：37-42.

TANG Baoping，JIANG Yonghua，ZHANG Xiangchun. Feature extraction method of rolling bearing fault based on singular value decomposition-morphology filter and empirical mode decomposition transform[J]. Journal of Mechanical Engineering，2010，46(5)：37-42.

[4] 唐海英，欒軍英，鄭海起，等. 基于階次跟蹤和經驗模態分解的滾動軸承包絡解調分析[J]. 機械工程學報，2007，43(8):119-122.

TANG Haiying， LUAN Junying， ZHENG Haiqi， et al. Envelope demodulation analysis of bearing based on order tracking and empirical mode decomposition[J]. Journal of Mechanical Engineering，2007，43(8):119-122.

[5] CHENG Junsheng，YU Dejie，YANG Yu. Energy operator demodulating approach based on EMD and its application in mechanical fault diagnosis[J]. Chinese Journal of Mechanical Engineering，2004，40(8)：115-118.

[6] LI Hui，ZHANG Yuping，ZHENG Haiqi. Hilbert-Huang transform and marginal spectrum for detection and diagnosis of localized defects in roller bearings[J]. Journal of Mechanical Science and Technology，2009，23(2):291-30.

[7] 唐先廣，郭瑜，丁彥春. 基于獨立分量分析與希爾伯特-黃變換的軸承故障特征提取[J]. 振動與沖擊，2011，30(10): 45-49.

TANG Xianguang，GUO Yu，DING Yanchun. Application of hilbert huang transition and independent components analysis on rolling element bearing faults features extraction[J]. Journal of Vibration and Shock，2011，30(10): 45-49.

[8] 蘇文勝，王奉濤，張志新. EMD降噪和譜峭度方法在滾動軸承早期故障診斷中的應用[J]. 振動與沖擊，2010，29(3): 18-21.

SU Wensheng，WANG Fengtao，ZHANG Zhixin，et al. Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearings[J]. Journal of Vibration and Shock，2010，29(3): 18-21.

[9] 高強，杜小山，范虹，等. 滾動軸承故障的EMD診斷方法研究[J]. 振動工程學報，2007，20(1): 15-18.

GAO Qiang，DU Xiaoshan，FAN Hong，et al. An empirical mode decomposition based method for rolling bearing fault

diagnosis[J].Journal of Vibration Engineering，2007，20(1): 15-18.

[10] 陳略，訾艷陽，何正嘉,等.總體平均經驗模式分解與1.5維譜方法的研究[J].西安交通大學學報，2009，43(5):94-98.

CHEN Lue，ZI Yanyang，HE Zhengjia，et al. Research and application of ensemble empirical mode decomposition principle and 1.5 dimension spectrum method[J]. Journal of Xi’an Jiaotong University，2009，43(5):94-98.

[11] 胡愛軍，馬萬里，唐貴基. 基于集成經驗模態分解和峭度準則的滾動軸承故障特征提取方法[J]. 中國電機工程學報， 2012，32(11):106-111.

HU Aijun，MA Wanli，TANG Guiji. Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion[J]. Proceedings of the CSEE，2012，32(11):106-111.

[12] 蔡艷平，李艾華，石林鎖，等. EMD 端點效應的改進型混沌延拓方法及其在機械故障診斷中的應用[J]. 振動與沖擊，2011，30(11)：46-52.

CAI Yanping，LI Aihua，SHI Linsuo，et al. Processing method for end effects of EMD based on improved chaos forecasting model and its application in machinery fault diagnosis[J]. Journal of Vibration and Shock，2011，30(11)：46-52.

[13] 曹沖鋒，楊世錫，楊將新. 一種抑制EMD 端點效應新方法及其在信號特征提取中的應用[J]. 振動工程學報，2008，21(6)：589-593.

CAO Chongfeng，YANG Shixi，YANG Jiangxin. A new method for restraining the end effect of empirical mode decomposition and its applications to signal feature extraction[J]. Journal of Vibration Engineering，2008，21(6)：589-593.

[14] ANTONI J，RANDALL R B. The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines[J]. Mechanical Systems and Signal Processing，2006，20(2): 308-331.

[15] LIN L， WANG Y， ZHOU H. Iterative filtering as an alternative algorithm for empirical mode decomposition[J]. Advances in Adaptive Data Analysis，2011，1(4):543-560.

[16] MC FADDEN P D，SMITH J D. Model for the vibration produced by a single point defect in a rolling element bearing[J]. Journal of Sound and Vibration，1984，96(1): 69-82.