雙臂工業機器人設計與協調運動研究

王勇， 黃俊杰， 鄭彬峰， 周際

（合肥工業大學 機械工程學院，合肥 230009）

0 引言

隨著智能裝備自動化技術、多傳感系統信息融合技術等科學技術不斷發展，機器人技術的應用領域越來越廣泛[1]，使用工況越來越復雜，經常需要通過兩個或多個操作臂協調操作來實現單臂機器人無法完成的作業任務[2]。

雙臂機器人需要兩個操作臂之間的雙臂協調控制[3-4]，GUO Yi-shen等[5]提出了通過自適應神經網絡控制雙臂空間機器人系統協調運動過程中的不確定參數，Rodrigo S.Jamisola Jr.等[6]提出了針對雙臂機器人的模塊化、組合化設計方法。關于雙臂機器人在裝配過程中的應用研究方面，彭鍵清[7]對雙臂空間機器人執行在軌裝配任務中需要雙臂協調操作的問題進行了研究，提出了目標捕獲前及捕獲后的雙臂協調軌跡規劃算法；魏明明等[8]將移動機器人行為動力學理論擴展到操作機器人三維空間，應用到機器人軸孔裝配中，并證明了其可行性。上述方法的計算和運用過程都相對復雜，本文擬設計可分別應用于圓柱體零件的軸向約束裝配和徑向約束裝配這兩種工況下的雙臂工業機器人，通過運動學、動力學仿真驗證模型可行性，并分析雙臂協調規劃方法。

1 用于典型工況的雙臂工業機器人結構設計

1.1 兩種典型工況特點分析

軸向約束裝配和徑向約束裝配是圓柱體零件典型裝配，其中具有代表性的是軸孔裝配和對稱圓盤類裝配，如圖1所示。現針對這兩類裝配的特點進行分析，并以此來設計合適的本體機構。

軸孔裝配和對稱圓盤類的裝配過程自動化，可通過雙臂工業機器人的協調控制來實現。其中軸孔裝配過程需要使兩軸線在裝配過程中時刻保持重合，并對兩零件沿中軸線的相對運動進行控制；對稱圓盤類零件的裝配過程中，要保證在裝配工作完成時兩零件的裝配部分能夠完全重合。

圖1 軸孔裝配和對稱圓盤類裝配示意圖

1.2 兩種典型工況雙臂工業機器人結構設計

這兩類裝配實際上都可以抽象為一維的直線運動，但考慮到實際工作中的上下料等問題，同時增加機器人的通用性，需要對其工作空間進行拓展。SCARA機器人具有結構輕便、響應快，適用于平面定位，垂直方向升降作業等特點，現基于SCARA機器人對雙臂工業機器人進行本體結構設計。

圖2 兩種典型工況雙臂工業機器人結構示意圖

雙臂工業機器人如圖2所示，其中用于軸孔裝配的工業機器人采用上下對稱布置，末端分別裝有吸附軸套零件的裝置；用于對稱圓盤類零件裝配工作的雙臂工業機器人左右對稱布置，末端裝有圓盤類零件的夾持裝置。根據實際工況，將雙臂工業機器人各單臂本體主要技術參數確定如表1所示。

大小臂關節處均采用了伺服電動機與減速器和推力圓柱滾子軸承相聯合的驅動方式，腕部驅動方式選用電動機與同步帶和滾珠絲杠配合使用來實現轉動和直線升降運動。根據計算，各個關節的電動機選型如表2所示。

表1 雙臂工業機器人的基本技術參數表

2 雙臂工業機器人運動學與動力學分析

由于兩類雙臂工業機器人具有相同的單臂結構，這里以用于對稱圓盤類零件裝配工作的雙臂工業機器人為例，對雙臂工業機器人進行運動學和動力學分析，對上述的設計選型進行驗證。

2.1 雙臂工業機器人運動學分析

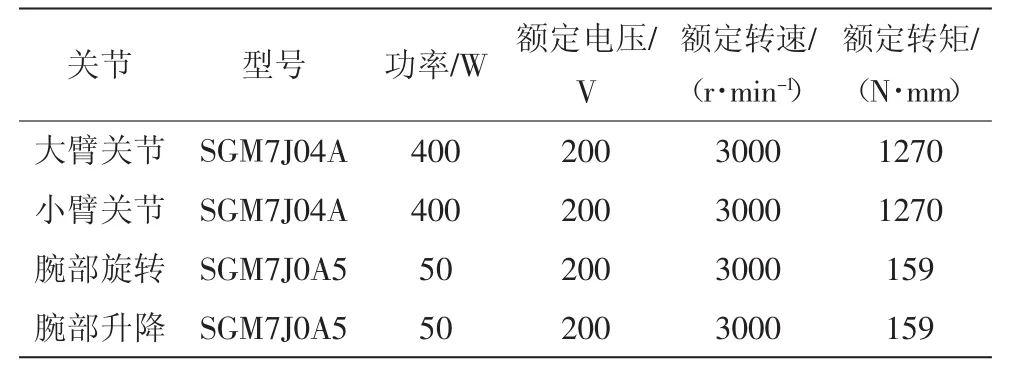
表2 關節電動機選型及其基本參數表

可建立雙臂工業機器人單臂的D-H模型，各參數如表3所示。

可建立機器人基座與手爪之間的正運動變換矩陣如式（1）：

表3 雙臂機器人的D-H參數表

借助Matlab Robotics Toolbox工具箱建立雙臂工業機器人參數模型，如圖3所示，顯示的是關節變量p1=［0,-pi/3,-5pi/8,-200,0］，p2=［pi,pi/3,5pi/8,-100,0］時機器人的形態，其中第一個關節變量表示基座。如圖3所示，得到的模型與通過正運動學公式計算得到的結果一致。

設置關節在初始和最終位置的關節變量分別為qz=［0,-pi/2,0,0,0］，qr=［0,-pi/3,-5*pi/8,-100,0］，其中第一個關節變量為0是為了方便建模而將雙臂機器人的肩部固定，第四個關節變量表示末端執行器的豎直方向移動。采用5次多項式擬合法，仿真時間為3 s，采樣間隔為0.1 s，起始點和終止點之間采樣30個點，可以得到各關節角的變化情況，其中大臂關節和小臂關節角的位移、速度、加速度的變化情況如圖4所示。

圖3 p1=［0,-pi/3,-5pi/8,-200,0］,p2=［pi,pi/3,5pi/8,-100,0］時機器人形態圖

圖4 大、小臂關節角位移、角速度、角加速度變化

得到的機器人大小臂關節角的變化曲線都是連續、平穩、光滑的，沒有出現突變情況，無明顯的沖擊和振動，保證雙臂機器人運動的平穩性。

2.2 雙臂工業機器人動力學仿真

將得出的大臂和小臂關節位移變化的數據離散點導入到ADAMS中，作為大臂和小臂關節的驅動，用于對雙臂機器人進行動力學仿真分析。將載荷和驅動定義好之后，將仿真時間設置為3 s，仿真步數設置為5000。得到大臂關節和小臂關節的驅動力矩變化如圖5所示。

圖5 大、小臂鉸接點處力矩大小變化

可以看出曲線平滑，沒有出現較大波動，滿足穩定性要求；大、小臂關節處所受最大力矩分別為為361.26 N·mm和613 N·mm，均小于電動機額定轉矩1270 N·mm，滿足使用要求。

由運動學和動力學分析結果，可知本文設計的雙臂工業機器人本體結構設計合理可行。

3 兩種典型工況下雙臂工業機器人運動規劃方法

根據運動特點，雙臂工業機器人本體結構只有豎直方向上的平移運動和旋轉運動，運用投影法將機器人轉換成二維數學模型，以下分別對雙臂工業機器人的協調運動規劃方法進行說明。

3.1 軸孔裝配雙臂工業機器人運動規劃方法

如圖6所示，裝配過程中的軸、孔零部件軸線始終平行，不需要對機器人末端位姿的協調計算工作。ABC與A′B′C′分別是左臂與右臂的初始位置，o為AA′中點。α、α′分別AB、A′B′與x軸的夾角，β、β′分別AB與BC，A′B′與B′C′的夾角。設OA=OA′=a，AB=A′B′=b，BC=B′C′=c，則有：A點坐標（xA,yA），B點坐標（xB,yB），C點坐標（xC,yC），有：

圖6 用于軸孔裝配的雙臂工業機器人運動規劃示意圖

這里若通過C點坐標直接求解α、β，會出現2個解，因此可先通過B點坐標確定α的值，再根據C點坐標求β的值。當左臂末端執行器移動至設定的D（xD,yD）處時，左臂處于AB1C1位置。根據式（2），同理對D點的坐標有：

式（3）中，α1、β1為未知量，求解過程中會有2組解，這里可通過比較的值，選取較小的那組作為需要的解。左臂運動過程即大臂轉角α→α1，小臂轉角β→β1。當兩臂末端投影移動到同一位置時，軸、套零件中軸線重合，通過腕部升降、旋轉兩關節配合運動，可完成裝配任務。右臂同理。

3.2 對稱圓盤類裝配雙臂工業機器人運動規劃方法

如圖7所示，ABC與A′B′C′分別是左臂與右臂初始位置，左臂與右臂沿中軸線對稱，因此有α=α′=β=β′，且BC和B′C′沿中軸線對稱；CD和C′D′分別表示夾持裝置，保持夾持裝置方向與小臂平行并固定。根據零件尺寸，可計算得到各關節所需轉動的θ角。若左右大臂、小臂運動規律相同，設為θ（t），則有：α+θ（t）= β+θ（t）=α′+θ（t）=β′+θ（t），即BC與B′C′時刻都保持平行且沿中軸線對稱，同時末端執行器也能保證對齊，保證了待裝配兩零件也能夠對齊。由于對稱圓盤這種特殊形狀，裝配過程中兩零件不會發生碰撞。

圖7 用于對稱圓盤類裝配的雙臂工業機器人運動規劃示意圖

4 結論

本文針對圓柱體零件的軸向約束和徑向約束這2種典型裝配工況下的雙臂機器人分別提出了可行方案，基于SCARA機器人設計出簡單可行的本體結構，避免了對雙臂協調、避障等方面所要做的大量計算工作，提高了雙臂機器人的實用性和可操作性，也為雙臂工業機器人應用于徑向與軸向約束裝配時的協調運動控制方法研究提供了新的思路。

[參 考 文 獻]

[1] 王東署,朱訓林.工業機器人技術與應用[M].北京：中國電力出版社,2016.

[2] 趙京.冗余度機器人、彈性關節冗余度機器人及其協調操作的運動學和動力學研究[D].北京：北京工業大學,1997.

[3] ZHENG Y F,LUH J Y S.Optimal load distribution for two industrial robots handling a single object[C]//IEEE International Conference on Robotics and Automation.1988：344-349.

[4] LEE S.Dual redundant arm configuration optimization with task-oriented dual arm manipulability[J].IEEE Transactions on Robotics&Automation,1989,5(1)：78-97.

[5] GUO Yishen,CHEN Li.Adaptive neural network control for coordinated motion of a dual-arm space robot system with uncertain parameters[J].Applied Mathematics and Mechanics,2008,29(9)：1131-1140.

[6] JAMISOLA R S JR,KORMUSHEV P S,ROBERTS R G,et al.Task-Space Modular Dynamics for Dual-Arms Expressed through a Relative Jacobian[J].Journal of Intelligent&Robotic Systems,2016,83(2)：205-218.

[7] 彭鍵清.雙臂空間機器人捕獲與操作目標的協調控制研究[D].哈爾濱：哈爾濱工業大學,2014.

[8] 魏明明,傅衛平,蔣家婷,等.操作機器人軸孔裝配的行為動力學控制策略[J].機械工程學報,2015,51(5)：14-21.