耦合勢有限體積法模擬海洋移動導線源三維頻率域電磁響應

周建美 李 貅 戚志鵬(長安大學地質工程與測繪學院,陜西西安 710054)

1 引言

海洋可控源電磁法(MCSEM)是一種重要的海上油氣勘探方法[1,2]。典型的MCSEM勘探采用水平導線源(長度一般為幾百米)隨船拖拽移動發射低頻信號，在海底布設接收機陣列測量水平電場和三分量磁場響應[3]。在海洋電磁勘探設計及資料處理和解釋過程中,均需要進行大量的數值模擬。三維正演算法研究一直都是電磁法的研究熱點。MCSEM的三維正演相比其他電磁方法，有其特殊性：由于海水的濾波作用，MCSEM的工作頻率非常低(0.1～10Hz)，導致控制方程呈病態，出現所謂的低感應數問題[4]； MCSEM的數值模擬需要同時計算近區和遠區的電磁場響應(如發射源頻率為0.25Hz時一般需要求解發射源附近±15km范圍內的電磁場分布)，由于在大區域范圍內電磁場的近場和遠場的振幅相差很大(10個數量級以上),同時由于空氣層的存在使得模型電導率差很大,導致離散化方程的條件數非常大[5]； MCSEM是一種典型的移動源電磁方法，需要對多次移動源進行三維模擬[6]。

目前主要采用有限差分法(FDM)[7-10]、有限體積法(FVM)[11]和有限元法(FEM)[12]模擬復雜三維地形的MCSEM響應。這三種方法的共同點是直接對Maxwell方程進行離散處理，得到一個大型的稀疏代數方程，借助于迭代法[13]或直接法[14]得到方程的數值解。直接法由于其對于矩陣的條件數不敏感,矩陣求解穩定,能有效處理移動源的三維正演問題[15]，廣泛應用于MCSEM電磁響應的數值模擬[12,14]，但直接法的內存需求和計算時間隨著未知數個數呈指數增長[16]，極大地制約了直接法用于復雜模型三維正演計算的效率。低感應數問題和大條件數的系數矩陣使常規的迭代算法很難有效求解MCSEM的離散線性方程[5]。利用電場的矢勢和標勢分解可有效克服低感應數問題[17]，結合有效的預處理能夠實現MCSEM離散的大條件數線性方程的求解[5,13,18]。

在MCSEM三維正演計算中，一般將導線源近似為電偶極源。對于電偶極源采用直接離散源項的方法，但電偶極源的奇異性將導致源附近區域存在較大的離散誤差。目前主要采用一次場/二次場方法利用等效源[13,14]或者差異場技術[15]克服源的奇異性問題。一次場/二次場方法能夠有效模擬復雜場源形態的MCSEM三維響應[14]，但需要額外計算所有網格節點上的一次場分布；差異場技術雖然能夠消除源附近的離散誤差，但需要兩次三維正演計算。對于實際MCSEM勘探中采用導線源的源項直接離散技術，這不同于電偶極源，在保證離散網格較導線源長度足夠小時可得到源附近較為精確的電磁場分布。

MCSEM是一種典型的移動源電磁方法。對于移動源三維正演計算，常規迭代算法設置迭代初始解為零，總的計算時間隨著移動源個數呈線性增長。設定移動發射源位置為網格中心位置，發射源移動，離散網格大小不變，但整體隨著發射源移動。由于發射源移動前后地下電性分布變化不大，因此發射源移動前后的電磁場分布也非常接近。選擇發射源移動前的電磁場分布作為發射源移動后電磁場的初始解，將有效減少迭代次數從而減少總的計算時間。

本文從Maxwell方程出發，首先通過引入電場的矢勢標勢分解，將Maxwell方程轉化為一個關于矢勢和標勢的混合亥姆霍茲方程定解問題[17]；采用洛倫茲規范[16]，借助Yee氏交錯網格和FVM對旋度和散度算子進行離散，得到稀疏對稱系數矩陣的離散方程；采用直接加源技術實現導線源的離散；采用基于ILUT預處理的BICGSTAB迭代算法[17]實現離散方程的迭代求解。采用改進的迭代算法實現移動源的快速正演，即采用發射源移動前的電磁場響應作為發射源移動后的電磁場分布的初始解，從而提高迭代收斂速度，減少計算時間。

2 耦合勢有限體積算法

2.1 控制方程

設電磁場隨時間變化關系為eiω t，MCSEM三維正演對應的控制方程為

(1)

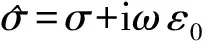
(2)

(3)

(4)

為了保證控制方程的完整性，對式(1)兩邊求散度，得到

(5)

將式(5)展開并利用洛倫茲規范進行簡單的整理，得到

(6)

將式(4)與式(6)聯立，表示為矩陣形式

(7)

(8)

由式(8)可知，該控制方程的系數矩陣是稀疏對稱陣。采用x方向的線電流源，式(8)進一步簡化為

D1Ax+Cxφ=-iωμ0Jx

(9a)

D1Ay+Cyφ=0

(9b)

D1Az+Czφ=0

(9c)

(9d)

邊界處采用簡單的截斷邊界條件[9]

(A,φ)|?Ω=0

(10)

式中Ω為求解區域。

2.2 有限體積離散

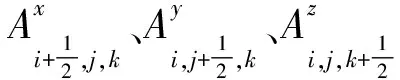
式(9a)對應于x方向的稀疏矩陣方程的有限體積離散，引入x方向對應的半整數控制體積單元

(11)

(12)

定義控制體積單元內的場值是均一的，則有

(13)

(14)

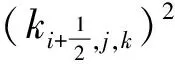
式(9b)～式(9d)左邊項的有限體積離散形式與式(9a)類似。

2.3 源項直接離散

源項離散包括式(9a)和式(9d)右邊項的有限體積離散。

對于式(12)右邊項的離散，本文采用直接加源方式。為了簡單起見，設定網格與發射源位置重合，發射源的兩個端點分別為(xa,yc,zd)和(xb,yc,zd)，其中xa和xb分別對應x方向相鄰的兩個網格節點坐標，yc和zd分別為y方向和z方向某一網格節點坐標，則沿x方向長度為xb-xa的線電流源可以定義為

Jx=Iδ(y-yc)δ(z-zd)×

[H(x-xb)-H(x-xa)]

(15)

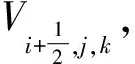
(16)

對于式(9d)右邊源項的有限體積離散，對應的控制體積單元為

(17)

對于x方向的發射源

[δ(x-xb)-δ(x-xa)]

(18)

則對應的有限體積離散為

(19)

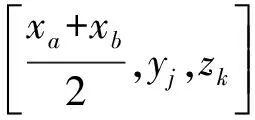
2.4 移動源控制方程的快速求解

對離散結果進行整理,得到關于矢勢A和標勢φ的方程組

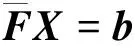
(20)

3 算法驗證

3.1 精度驗證

通過與一維模型的半解析計算結果進行對比，驗證FVM的計算精度； 通過對比偶極源與線源的計算精度，驗證源項直接離散方法的有效性。一維模型如圖1所示，空氣層電阻率設為1.0×106Ω·m，海水層電阻率為0.25Ω·m，海水層厚度為1000m，海底地層電阻率為1.0Ω·m。分別計算發射源為x方向的水平電偶極源(長度為1m)和線源(長度為400m)兩種情況，發射源極矩均為1A·m，發射源位于海底上方100m，發射頻率為0.25Hz。接收機位于海底，接收沿測線方向的電場Ex。剖分網格單元數為121×121×101，最小網格長度為100m，即線源為4個網格長度，偶極源為1個網格長度，總的網格剖分范圍如圖1所示。分別采用基于ILUT預處理的BICGSTAB算法和基于Jacobi預處理的QMR算法[14]求解該一維模型。圖2為采用電偶極源時兩種算法的收斂曲線對比，得到小于1.0×10-8的歸一化殘差，基于Jacobi預處理的QMR算法需要3316次迭代，計算時間為918s；而基于ILUT預處理的BICGSTAB算法只需要336次迭代，計算時間為416s， 可見后者計算速度更快，本文在后面的數值計算中都采用該算法。本文的FVM計算結果與開源軟件Dipole1D[19]的半解析計算結果對比如圖3所示,圖4為線源與偶極源響應結果對比。

圖1 海洋一維模型

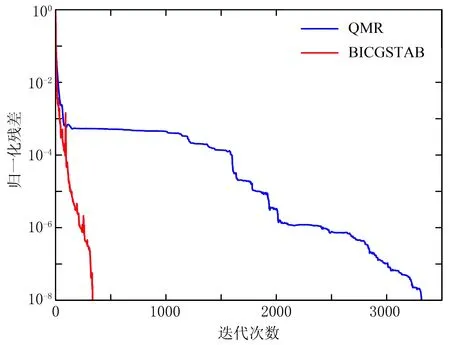
圖2 兩種迭代求解算法的收斂曲線對比

對比圖4a與圖4b可知，線源與偶極源的響應只是在發射源附近區域(偏移距小于2500m)存在差異(圖3中的紅色曲線清晰地顯示了在發射源附近區域兩種發射源響應的差別)，在偏移距大于2500m的區域，兩種場源的響應基本相同，與文獻[20]的結論一致。對于MCSEM，異常一般都出現在大偏移距區域，因此MCSEM采用偶極源近似線源是合理的。由圖4c可知，在偏移距大于2500m的區域， FVM計算的線源與電偶極源的振幅的相對誤差基本一致，均小于3%；在發射源附近，FVM計算的電偶極源振幅的相對誤差較大，達到了23%，線源振幅的最大相對誤差小于7%。由圖4d可知，不論是電偶極源還是線源，在整個求解區域(包括源所在位置)的相位差均小于2°； 線源發射的情況下，源區域的相位差更小。綜合圖4c和圖4d可知：①對電偶極源采用直接加源技術，會導致源附近區域的振幅存在較大誤差；②對線源采用直接加源技術，并保證源附近區域網格長度相比發射源長度足夠小(本文中發射源長度為400m，源附近網格長度為100m)，能夠得到發射源附近區域較為精確的響應。

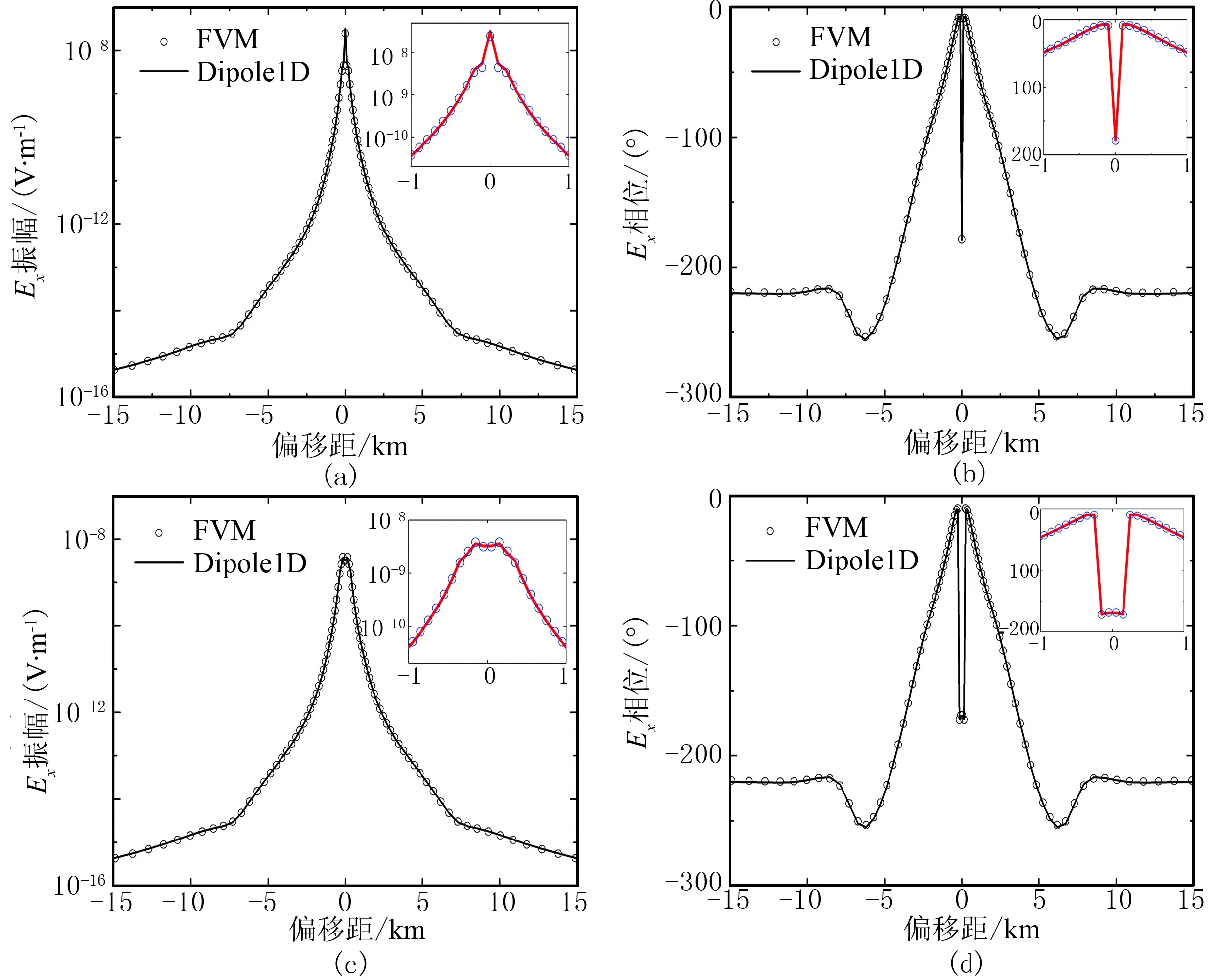
圖3 海洋一維模型正演響應(a)電偶極源的Ex振幅； (b)電偶極源的Ex相位； (c)線源的Ex振幅; (d)線源的Ex相位

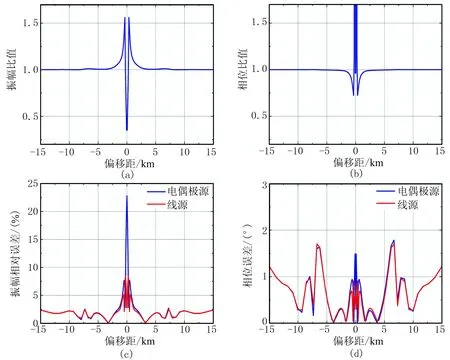
圖4 FVM計算的電偶極源與線源計算結果對比(a)線源與偶極源Ex振幅比值； (b)線源與偶極源Ex相位比值; (c)電偶極源和線源相

3.2 單異常體模型

本文采用迭代法計算移動源模型的三維正演，利用解的初值重置技術減少迭代次數從而減少計算時間。為了分析算法的有效性，設計如圖5所示的三維模型。在海底下方1000m處存在一個直徑4km、厚度100m、電阻率為100Ω·m的圓形高阻油氣藏。發射源為沿x方向、長度為400m的線電流源，置于海底上方100m，發射頻率為1.0Hz。發射源沿x方向移動，設定初始發射源與油氣藏中心在x方向的距離為2500m，每隔500m移動一次，共移動11次。接收機位于海底，接收沿測線方向的電場Ex。采用FVM算法計算該移動源模型，剖分網格單元數為141×121×112，最小網格長度為100m(圖6)。

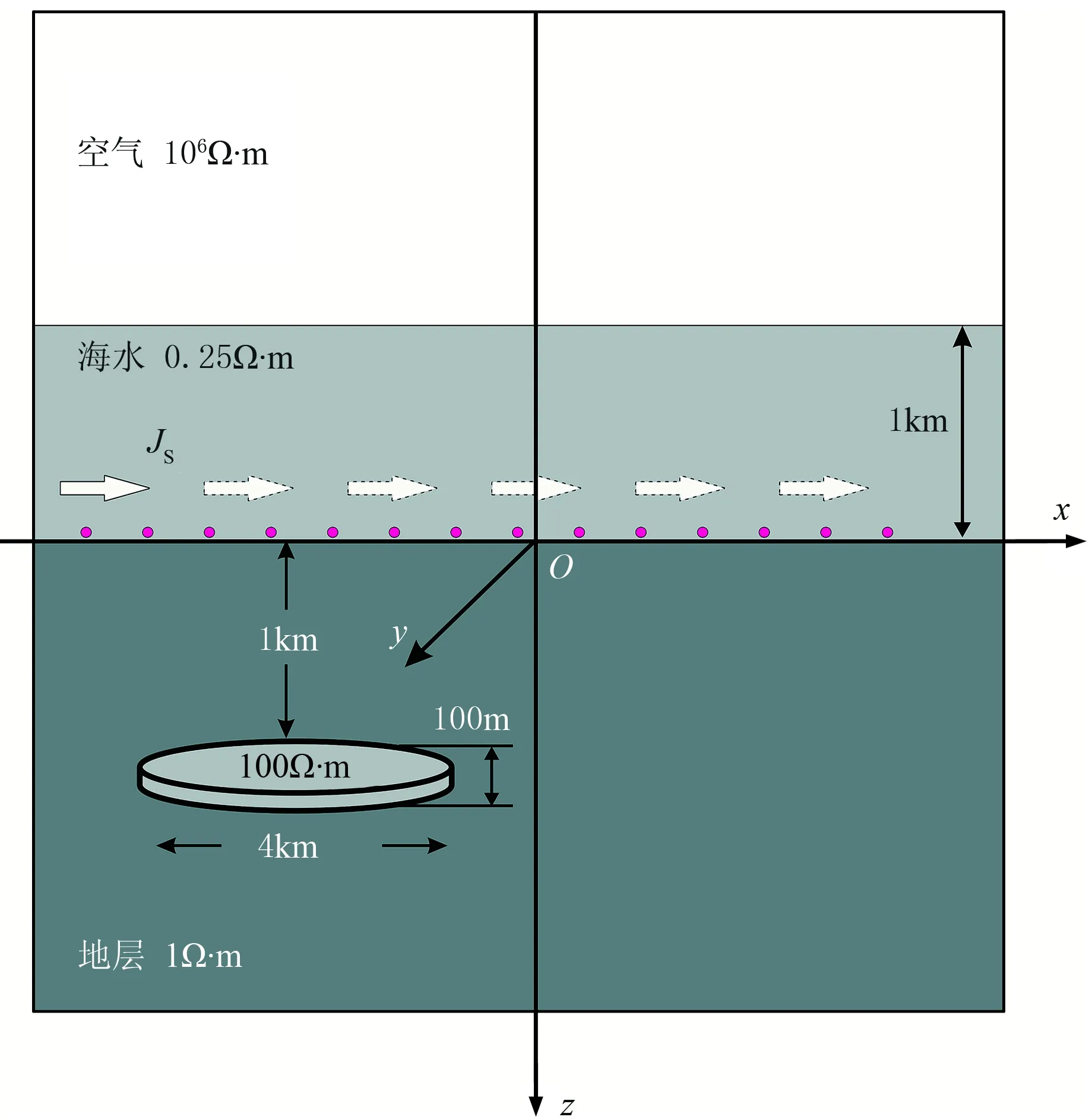
圖5 單異常體海洋三維模型

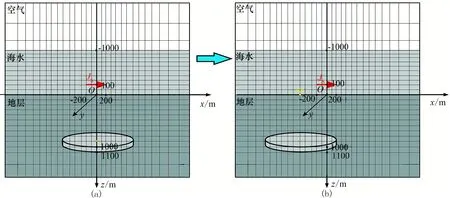
圖6 移動源海洋3D模擬網格剖分示意圖(a)發射源移動前； (b)發射源移動后

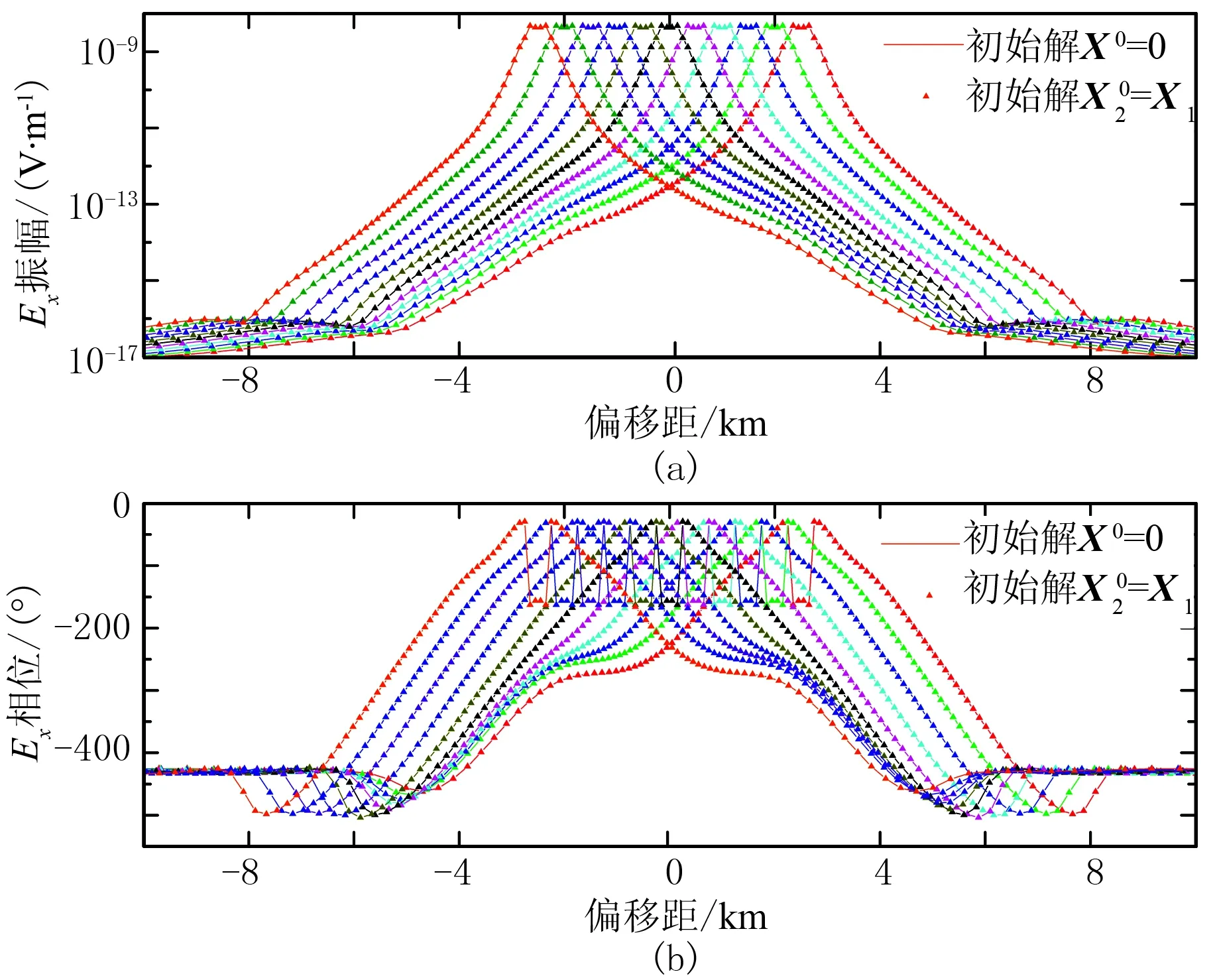
圖7 FVM計算的海洋移動源三維模型正演響應(a)Ex振幅； (b)Ex相位

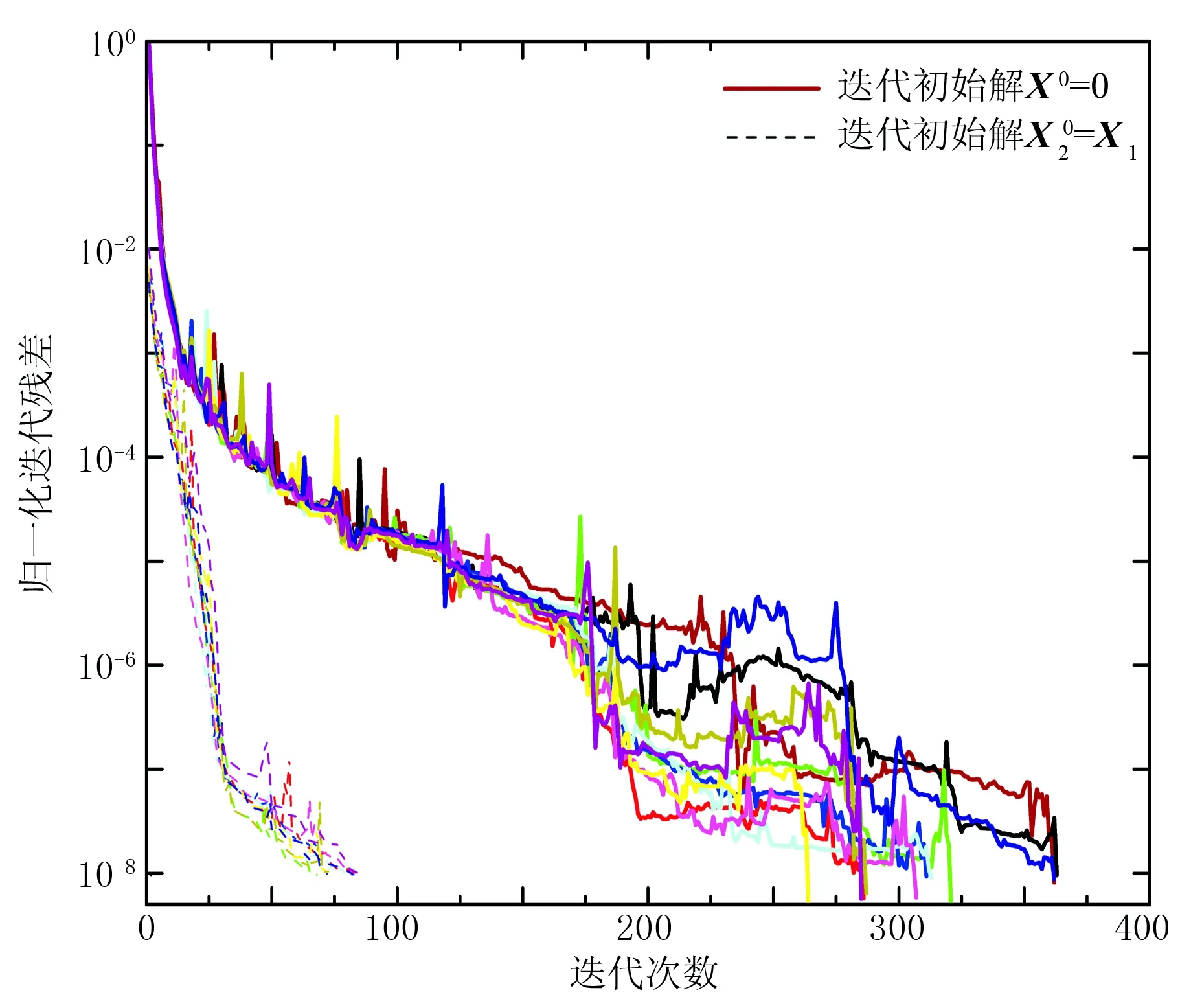
圖8 移動源正演計算迭代收斂曲線

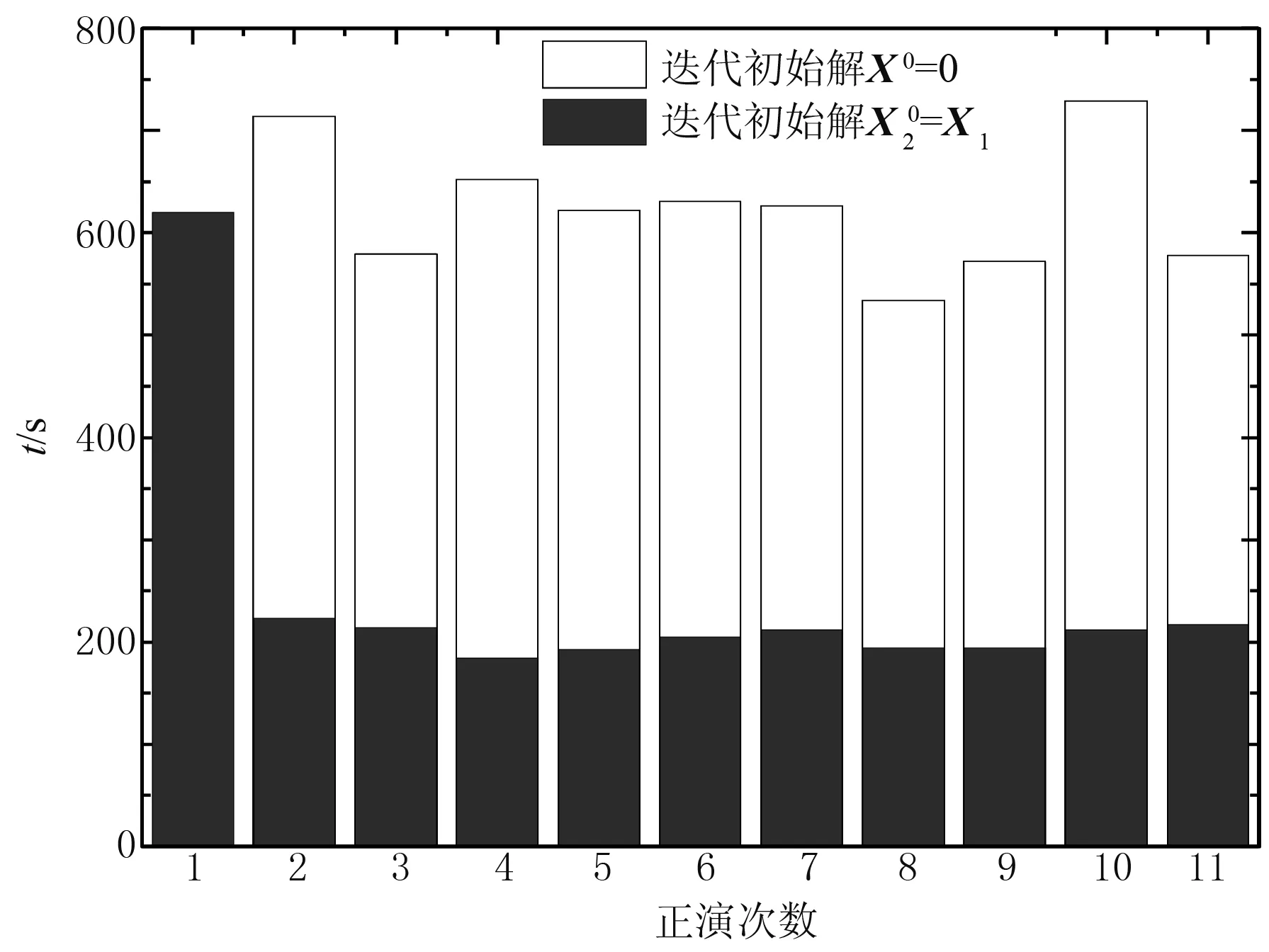
圖9 移動源正演響應計算時間對比

3.3 雙異常體模型

雙異常體三維模型如圖10所示。在海底下方1000m深度處存在兩個直徑為2km、厚度為100m、電阻率為100Ω·m的高阻油氣藏。發射源為沿x方向、長度為400m的線電流源，位于海底上方100m，發射頻率為1.0Hz, 發射源沿x方向移動。設初始發射源距離第一個目標體邊界在x方向上的距離為500m，每隔1000m移動一次，共移動7次。接收機位于海底，接收沿測線方向的電場Ex。剖分網格單元數為201×121×112，最小網格長度為100m，網格以發射源為中心。

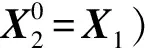
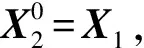
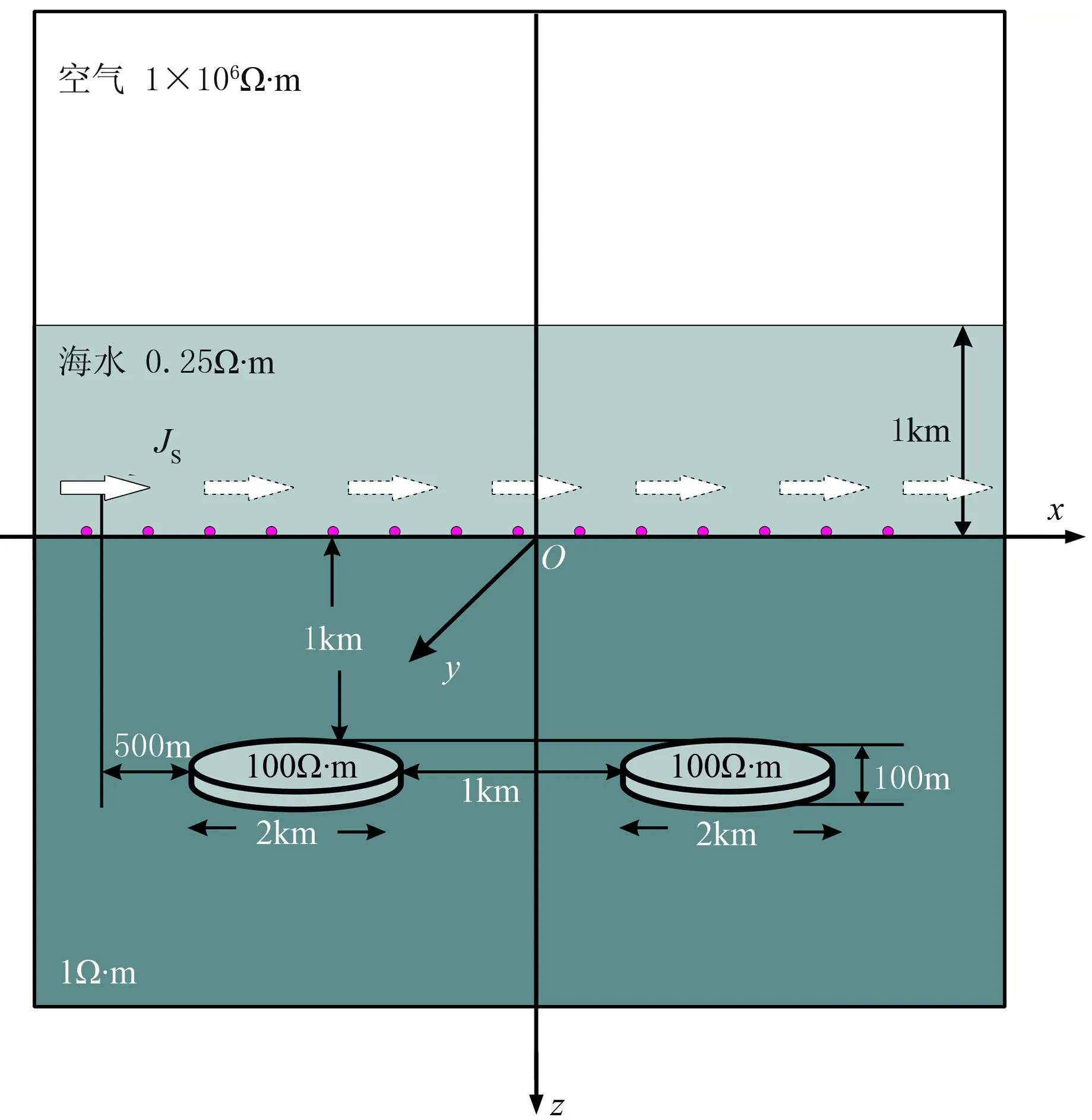
圖10 雙異常體模型

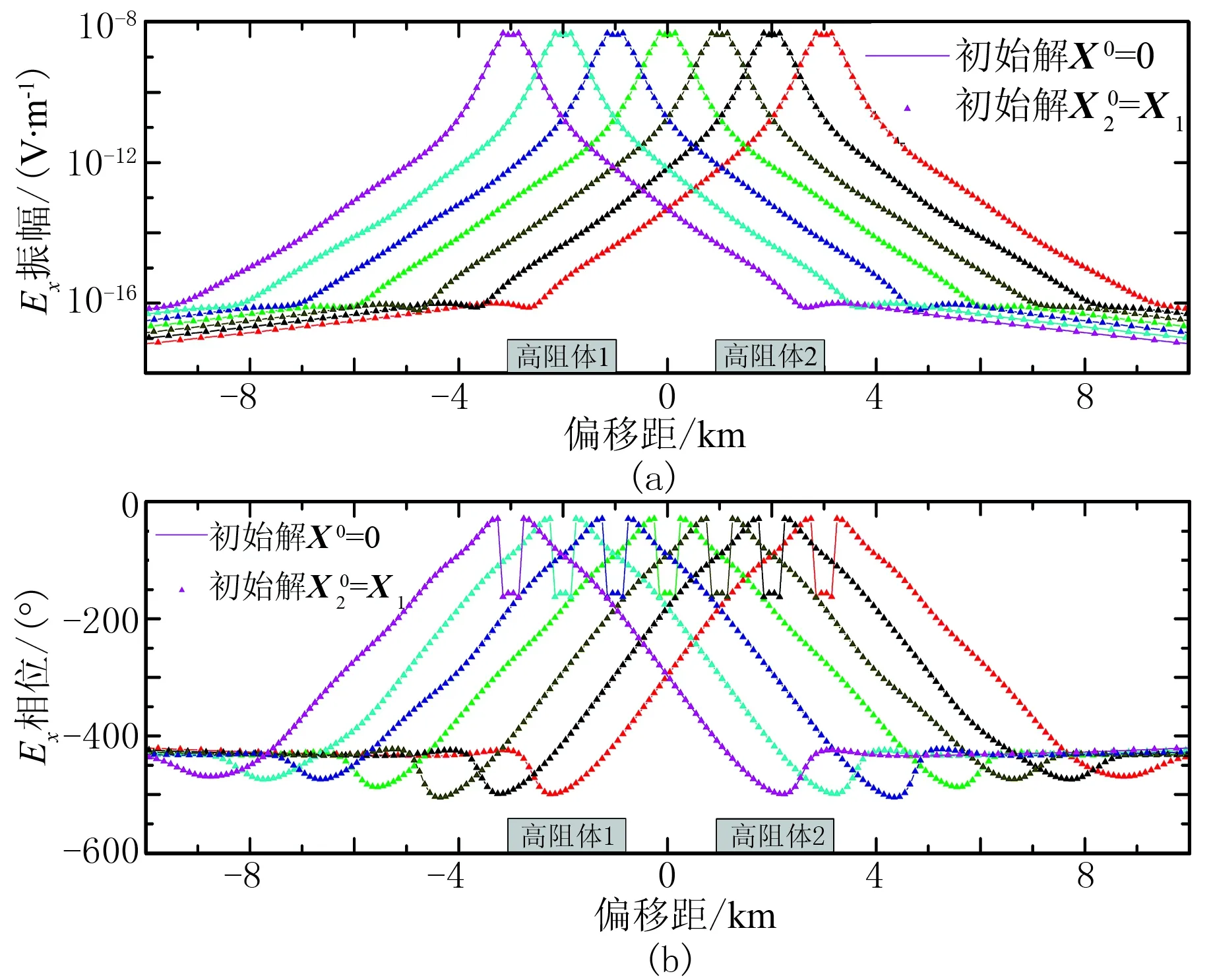
圖11 雙異常體模型正演響應(a)Ex振幅； (b)Ex相位

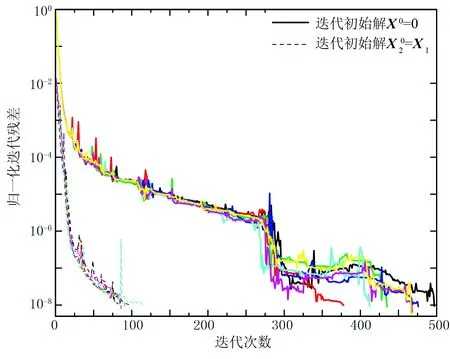
圖12 雙異常體模型移動源正演計算迭代收斂曲線

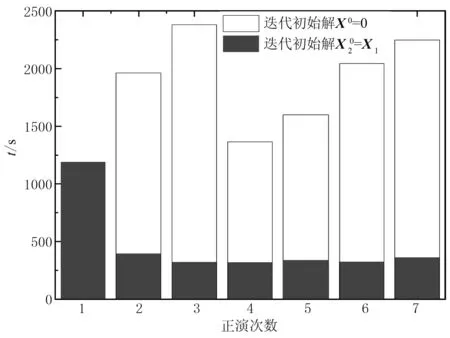
圖13 雙異常體模型移動源正演響應計算時間對比

3.4 非均勻覆蓋層模型

為了進一步研究本文算法的適用性，設計如圖14所示的非均勻覆蓋層的三維模型。 在海底下方1000m深度處存在一個直徑為4km、厚度為100m、電阻率為100Ω·m的圓形高阻油氣藏。海水下方覆蓋層中有兩個電阻率分別為10Ω·m和5Ω·m的三維異常體。發射源為沿x方向、長度為400m的線電流源，發射源始終保持在海底上方100m處，發射頻率為1.0Hz，發射源沿x方向移動。設定初始發射源距離高阻油氣藏異常體邊界在x方向上的距離為500m，每隔500m移動一次，共移動11次。接收機位于海底沿地形布設，接收沿測線方向的電場Ex。網格剖分單元為141×121×112，最小網格長度為100m，網格以發射源為中心。

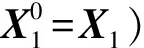
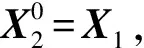
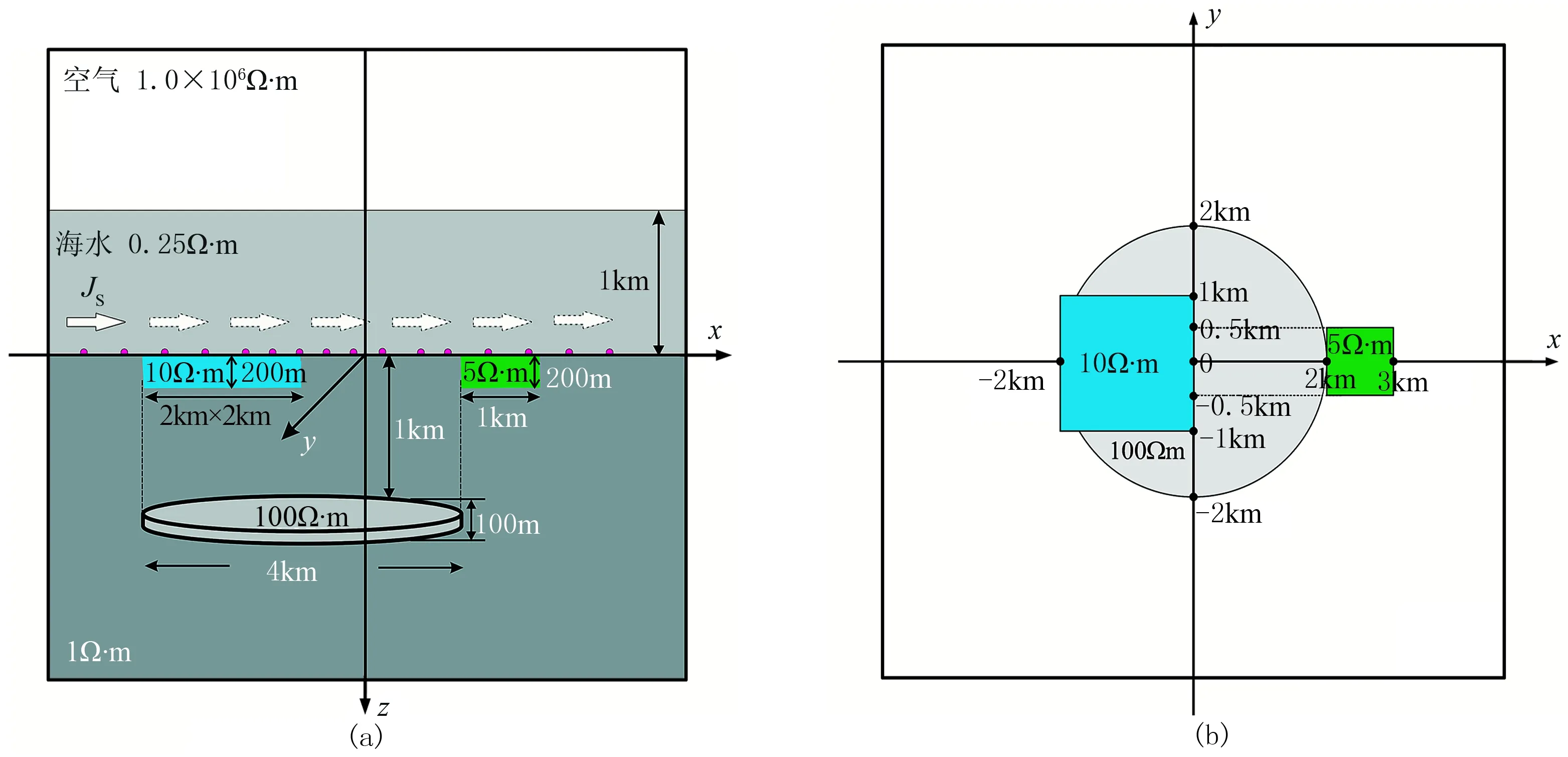
圖14 海洋非均勻覆蓋層三維模型(a)xoz平面圖； (b)xoy平面圖

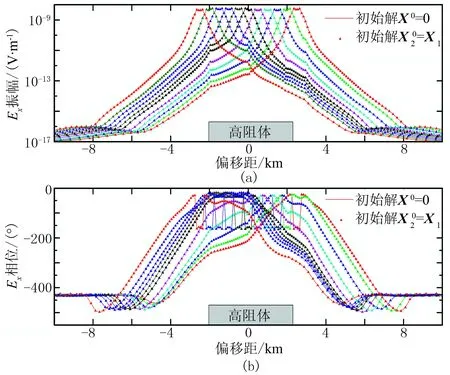
圖15 非均勻覆蓋層三維模型響應曲線(a)Ex振幅; (b)Ex相位

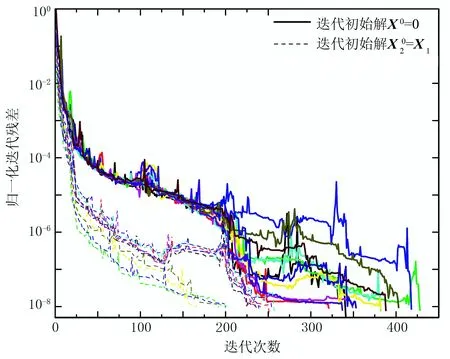
圖16 非均勻層覆蓋層模型的正演計算迭代收斂曲線對比

圖中實線為移動源11次正演常規算法(即迭代初始解X0=0)的迭代收斂曲線，虛線為本文改進算法(即迭代初始解X0=X1)計算的后10次正演(不包括第1次正演)的迭代收斂曲線

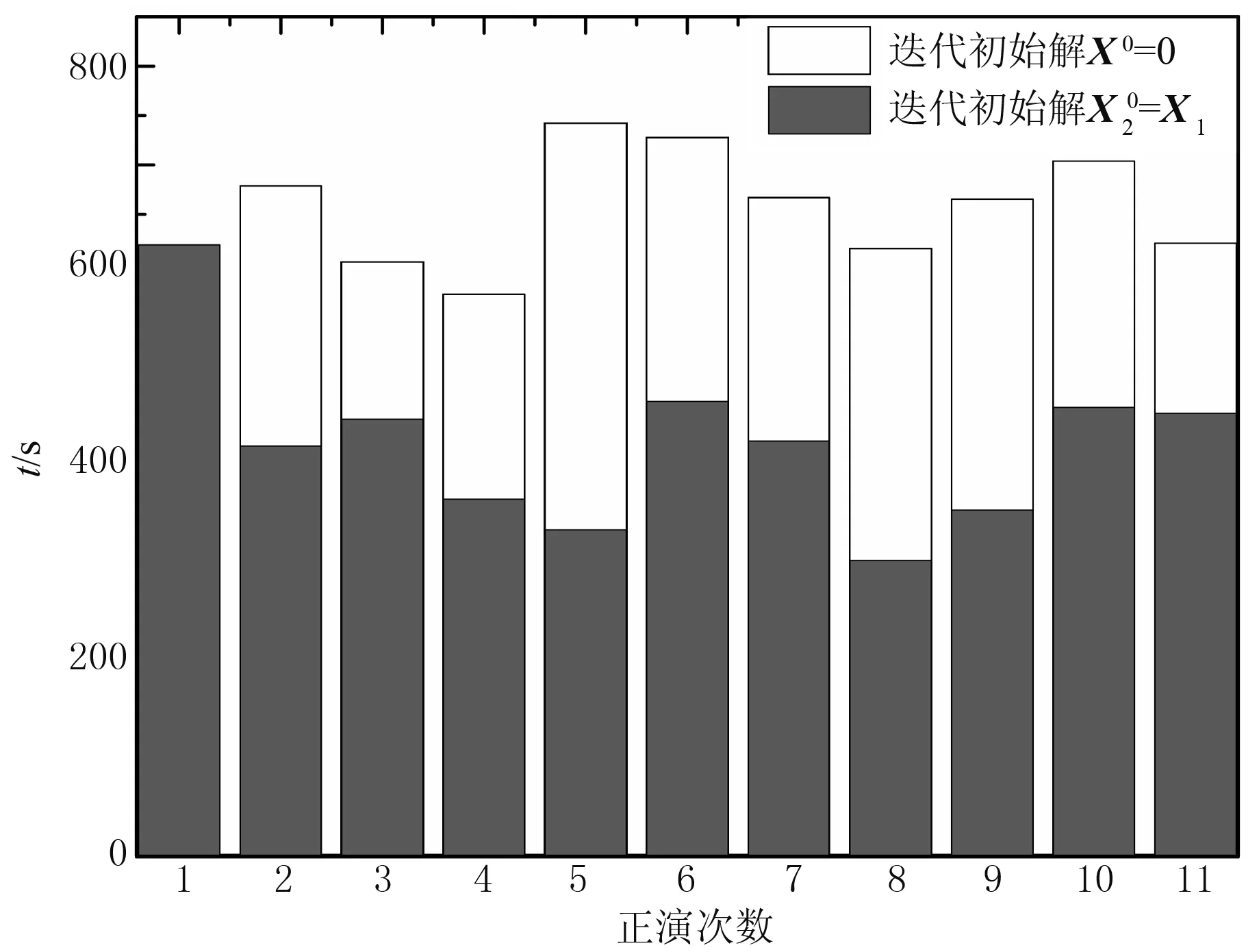
圖17 非均勻覆蓋層三維模型正演響應計算時間對比

4 結束語

本文采用耦合勢有限體積法建立了一套快速計算海洋移動導線源電磁響應的三維數值模擬技術：基于電場矢勢和標勢分解將Maxwell方程轉換為關于矢勢與標勢的亥姆霍茲方程；采用洛倫茲規范整理得到對稱形式的離散系數矩陣；通過基于ILUT預處理的BICGSTAB算法迭代求解離散線性方程；采用直接加源技術實現導線源的精確快速模擬；針對移動源正演響應計算，提出采用解的初值重置技術加快正演速度，即采用發射源移動前的電磁場響應作為發射源移動后電磁場分布的初始解，提高迭代收斂速度，減少迭代次數。

數值實例計算結果表明，采用直接加源技術，通過將導線源表示為多個電偶極源的疊加，能夠顯著減少源附近區域的計算誤差。對于移動源的正演計算，采用解的初值重置技術，選擇發射源移動前的電磁場分布作為移動后控制方程迭代計算的初始解，當發射源移動前后空間中電磁場分布變化較小時，能顯著地提高正演速度；當發射源移動前后空間中電磁場分布變化較大時，正演速度提高有限。

參考文獻

[1] Constable S.Ten years of marine CSEM for hydrocarbon exploration.Geophysics,2010，75(5):A67-A81.

[2] 何展翔,孫衛斌,孔繁恕等.海洋電磁法.石油地球物理勘探,2006,41(4):451-457.

He Zhanxiang,Sun Weibin,Kong Fanshu et al.Marine electromagnetic approach.OGP,2006,41(4):451-457.

[3] Constable S and Srnka L.An introduction to marine controlled-source electromagnetic methods for hydrocarbon exploration.Geophysics,2007,72(2):WA3-WA12.

[4] Newman G A and Alumbaugh D L.Three-dimensio-nal induction logging problems,Part 2:A finite-diffe-rence solution.Geophysics,2002,67(2):484-491.

[5] Puzyrev V.A parallel finite-element method for three-dimensional controlled-source electromagnetic forward modelling.Geophysical Journal International,2003,193(2):678-693.

[6] Plessix R E,Darnet M and Mulder W A.An approach for 3D multisource,multi frequency CSEM modeling.Geophysics,2007,72(5):SM177-SM184.

[7] 殷長春,賁放,劉云鶴等.三維任意各向異性介質中海洋可控源電磁法正演研究.地球物理學報,2014,57(12):4110-4122.

Yin Changchun,Ben Fang,Liu Yunhe et al.MCSEM 3D modeling for arbitrarily anisotropic media.Chinese Journal of Geophysics,2014,57(12):4110-4122.

[8] 付長民,底青云,王妙月.海洋可控源電磁法三維數值模擬.石油地球物理勘探,2009,44(3):358-363.

Fu Changmin,Di Qingyun,Wang Miaoyue.3D nume-ric simulation of marine controlled source electromagnetics (MCSEM).OGP,2009,44(3):358-363.

[9] 嚴波,李予國,韓波等.任意方位電偶源的MCSEM電磁場三維正演.石油地球物理勘探,2017,52(4):859-868.

Yan Bo,Li Yuguo,Han Bo et al.3D marine controlled-source electromagnetic forward modeling with arbitrarily orientated dipole source.OGP,2017,52(4):859-868.

[10] 朱成,李桐林,楊海斌等.帶地形頻率域可控源電磁法三維反演研究.石油地球物理勘探,2016,51(5):1031-1039.

Zhu Cheng,Li Tonglin,Yang Haibin et al.3D controlled source electromagnetic inversion with topography in the frequency domain.OGP,2016,51(5):1031-1039.

[11] 楊波,徐義賢,何展翔等.考慮海底地形的三維頻率域可控源電磁響應有限體積法模擬.地球物理學報,2012,55(4):1390-1399.

Yang Bo,Xu Yixian,He Zhanxiang et al.3D frequency-domain modeling of marine controlled source electromagnetic responses with topography using finite volume method.Chinese Journal of Geophysics,2012,55(4):1390-1399.

[12] 楊軍,劉穎,吳小平.海洋可控源電磁三維非結構矢量有限元數值模擬.地球物理學報,2015,58(8):2827-2838.

Yang Jun,Liu Ying,Wu Xiaoping.3D simulation of marine CSEM using vector finite element method on unstructured grids.Chinese Journal of Geophysics,2015,58(8):2827-2838.

[13] 蔡紅柱,熊彬,Michael Zhdanov.電導率各向異性的海洋電磁三維有限單元法正演.地球物理學報,2015,58(8):2839-2850.

Cai Hongzhu,Xiong Bin,Zhdanov M.Three-dimensional marine controlled-source electromagnetic mode-lling in anisotropic medium using finite element method.Chinese Journal of Geophysics,2015,58(8):2839-2850.

[14] 韓波,胡祥云,黃一凡等.基于并行化直接解法的頻率域可控源電磁三維正演.地球物理學報,2015,58(8):2812-2826.

Han Bo,Hu Xiangyun,Huang Yifan et al.3-D frequency-domain CSEM modeling using a parallel direct solver.Chinese Journal of Geophysics,2015,58(8):2812-2826.

[15] 周建美,張燁,汪宏年等.耦合勢有限體積法高效模擬各向異性地層中海洋可控源的三維電磁響應.物理學報,2014,63(15):159101-1.

Zhou Jianmei,Zhang Ye,Wang Hongnian et al.Efficient simulation of three-dimensional marine controlled-source electromagnetic response in anisotropic formation by means of coupled potential finite volume method.Acta Physica Sinica,2014,63(15):159101-1.

[16] Streich R.3D finite-difference frequency-domain mode-ling of controlled-source electromagnetic data:Direct solution and optimization for high accuracy.Geophy-sics,2009,74(5):F95.

[17] Haber E,Ascher U,Aruliah D et al.Fast simulation of 3D electromagnetic problems using potentials.Journal of Computational Physics,2000,163(1):150-171.

[18] Weiss C J. Project APhiD:a Lorenz-gauged A-decomposition for parallelized computation of ultra-broadband electromagnetic induction in a fully heterogeneous Earth.Computers & Geosciences,2013,58(1):40-52.

[19] Key K.1D inversion of multi component,multi frequency marine CSEM data:Methodology and synthetic studies for resolving thin resistive layers.Geophysics,2009，74(2):F9-F20.

[20] Streich R and Becken M.Electromagnetic fields ge-nerated by finite-length wire sources:comparison with point dipole solutions.Geophysical Prospecting,2011，59(2):361-374.