基于粒子群算法的樹狀灌溉管網系統優化設計

王文婷，郭乙霏

(1,焦作市抗旱防汛通訊站，河南 焦作 454150；2.東北農業大學水利與土木工程學院，哈爾濱 150003)

0 引 言

近年來，隨著我國經濟水平和人口數量的持續增長，我國的水資源供需不平衡、水資源不足等問題顯得日益突出，使我國農業現代化進程受到嚴重的制約。農業作為我國的用水大戶，具有巨大的節水潛力，因此節水農業的發展對緩解我國水資源供需不平衡，應對我國水資源不足等有著重要的意義。

在進行農田灌溉時，需要事先從水源地將灌溉水合理、有序、及時的運送到田間。灌溉水的運輸作為農業灌溉中不可或缺的環節，對我國節水農業的發展有著重要的意義。自20世紀七八十年代以來，灌溉管網在我國農田灌溉中的應用越來越廣泛。利用灌溉管網實現灌溉水的輸配在減少蒸發損失和輸水損失、提高灌溉水利用效率的同時，也在增大有效灌溉面積、提高土地利用率方面有著明顯的成效[1]。此外，灌溉管網系統移動靈活方便，灌溉效率高，容易實現自動化和方便田間管理[2, 3]。因此，在21世紀節水農業發展過程中，管道化灌溉起著舉足輕重的作用。

灌溉管網系統的優化設計主要是通過優化數學模型，借助數學方法和計算機技術，尋求模型的最優解，實現對管網系統的優化布置以及管網直徑的優化選擇，篩選出能使投資達到最小的優化方法[4-6]。近年來，國內外不少學者采用不同的計算方法(如遺傳算法、最小生成樹算法等)建立起了不同的灌溉管網優化模型，并實現了灌溉管網系統的優化布置。付玉娟[7]、馬雪琴[8]、Glodberg[9]等利用基于整數編碼遺傳算法對灌區樹狀管網進行優化布置，并通過實例驗證，均得到了較優的管網系統布置方案。而后，付亞娟又利用GIS技術對灌溉管網進行優化布置。胡杰華[10]、李密青[11]等則利用最小生成樹模型，也實現了灌溉管網系統的多目標優化布置。

粒子群算法(Particle Swarm Optimization，PSO)作為進化算法的一種，從隨機解出發，通過適應度來評估所得解的品質，依據追隨當前搜索到的最優解來找到全局的最優解，具有收斂快、精度高、易實現等特點[12]。目前，粒子群算法在石油運輸管網優化[13-15]和污水管網優化[16]中應用廣泛，甚至在配電系統中也有所應用[17-19]。在農田灌溉中，灌溉管網具有與石油、污水等運輸管網相似的特點，而PSO算法在農田灌溉管網系統優化布置方面的應用則鮮有報道。

本文在綜合分析粒子群算法原理和過程的基礎上，將其與樹狀灌溉管網模型相結合，實現了對灌區灌溉管網系統的優化，最后結合具體實例對我國某灌區灌溉管網系統進行優化并與2級遺傳優化模型進行對比，說明了粒子群算法的可行性和優越性。

1 樹狀灌溉管網數學模型的構建

為了達到灌溉管網造價最低的目標，在進行管網優化時，所使用的數學模型如下：

(1)

灌溉管網優化模型的約束條件如下。

(1)為了保證管網中各節點壓力滿足最小壓力，需滿足以下約束條件：

(2)

(2)流速約束條件：

Vmin≤Vi≤Vmaxi=1,2,…,n

(3)

式中：Vmin和Vmax分別表示管道允許的最小和最大流速，m/s。

(3)管徑約束條件。管道直徑需選擇標準的可用管徑，即：

Di∈[d1,d2,…,dM]

(4)

式中：Di表示管道直徑，mm；M表示可供選擇的管道直徑的個數；d1,d2,…,dM表示可供選擇的管道直徑，mm。

2 粒子群算法的實現

粒子群算法是基于鳥群捕食行為研究而建立的一種智能簡化算法，它最初由kennedy博士和Eberhart博士在1995年聯合提出的一種較新的算法[12]。與遺傳算法相類似，它也是進化算法的一種[14]。它首先初始化一組隨機解，然后借助隨機搜索的方法依據適應值來找尋最優值，在離散變量和連續變量的優化中應用較為廣泛。

整個PSO算法中，所有粒子都有一個適應度函數(用fit表示，其中fit=1/Z，即為管網總造價的倒數)。在整個研究空間中，所有粒子都有自己的飛行速度和方向，優化過程就是通過個體自身體驗(進行局部優化過程)和群體間的信息共享(進行全局優化過程)對粒子的飛行速度和方向進行不斷的調整和優化，從而使所有的粒子(整體)都“飛行”到最理想的區域中，因此，基于PSO優化算法的過程即為尋找研究空間中粒子的過程。PSO算法具體流程見圖1。

圖1 PSO算法基本實現過程

在PSO算法中，假定粒子群落大小為N(即由N個粒子構成)，在m維空間中對目標進行搜索。在優化過程中粒子位置和運動狀態信息主要是由Xi=(Xi1,Xi2,…,Xim)、Pibest、Vi(Vi1,Vi2,…,Vim)和gbest決定，它們分別表示粒子當前位置坐標、優化過程中的最優位置坐標(也即個體最優值)、粒子在該時刻的運動速度以及整個粒子群體在優化過程中的最優位置坐標(也即全局最優值)。各個粒子都是通過以下2個方程來調整其速度和方向的。

(5)

(6)

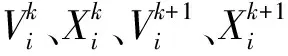
3 工程實例應用

3.1 已知條件

以我國某灌區為例，對該灌區的管網布置系統進行優化處理。考慮實際情況，在使用灌區樹狀灌溉管網進行供水時，各個結點必須滿足有且只有一個供水管道為其供水，這就需要從多個可能供水管道進行優化選擇，從而確定出所有結點的供水管道，組成最終的優化供水管網。該灌區中所有可能的灌溉管網布置見圖2，共10個供水節點(其中0點為水源點)，26種可能的供水連接方案。每個節點的進水管道按照逆時針方向用整數代碼進行命名，如圖2中的節點2，按照逆時針方向將3個供水管道依次編碼為0，1，2。該灌溉管網中可用的管道直徑和管道價格見表1，并按照管徑從小到大的順序依次編碼。在該管網系統中，允許最大和最小流速分別為3.0和0.5 m/s，壓力水頭為10 m。表2給出了各個管段編號及管段長度等。

圖2 某灌區灌溉管網初步布置

表1 可選用的管道規格

各個管段編號按照“流出結點-供水管道編碼-流入結點”的方式進行命名，例如：a-0-b。表3給出了0～9各供水結點高程和需水量等數據。

表2 灌溉管網中各管段長度 m

表3 灌溉管網中各個供水結點數據

3.2 模型計算結果

利用matlab 14a軟件進行對粒子群算法進行編程計算，本文中各系數取值如下：c1=0.5，c2=2.0，w=0.95，N=200，最大迭代次數為100，通過計算可得到造價最低且符合實際的最優方案。 PSO優化過程中適應度值變化情況見圖3。文中通過PSO優化得到的管網總長度為2 620 m，總投資金額為1.193 萬元。文獻[4]中通過2級優化遺傳模型優化得到的投資總金額和管網總長度見表4。通過比較可知PSO優化算法可減少3.7%的管網用量，減少27.8%的投資金額，同時在PSO算法中還給出了最優的管道組合，管道流速等信息，見表4。

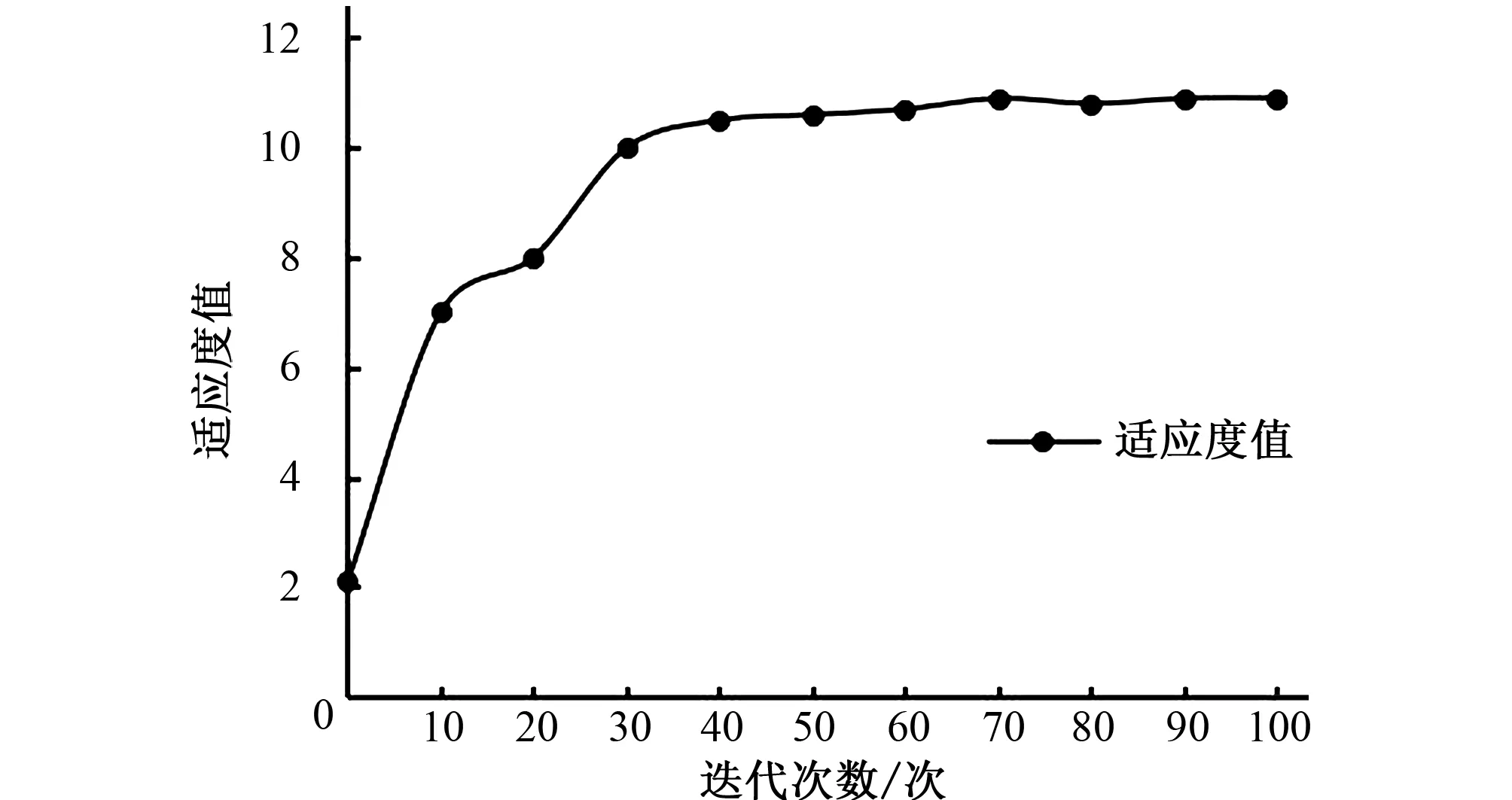
圖3 PSO算法優化過程適應度值變化情況

圖4和圖5分別給出了基于2級遺傳優化模型和基于PSO算法得到的灌區優化管網布置形式。在2級遺傳優化模型得到的管網優化布置形式中只有一個總投資額和總管長的優化值，并沒有說明管道流速和管道長度。所以在文獻[4]中的總投資額應是一個估計值，而實際值應較估計值略低。通過與原設計方案比較可知，使用PSO算法得到的灌溉管網優化結果中總投資額度更少，灌溉管網總長度也更短，有利于節約投資成本，且符合實際情況。

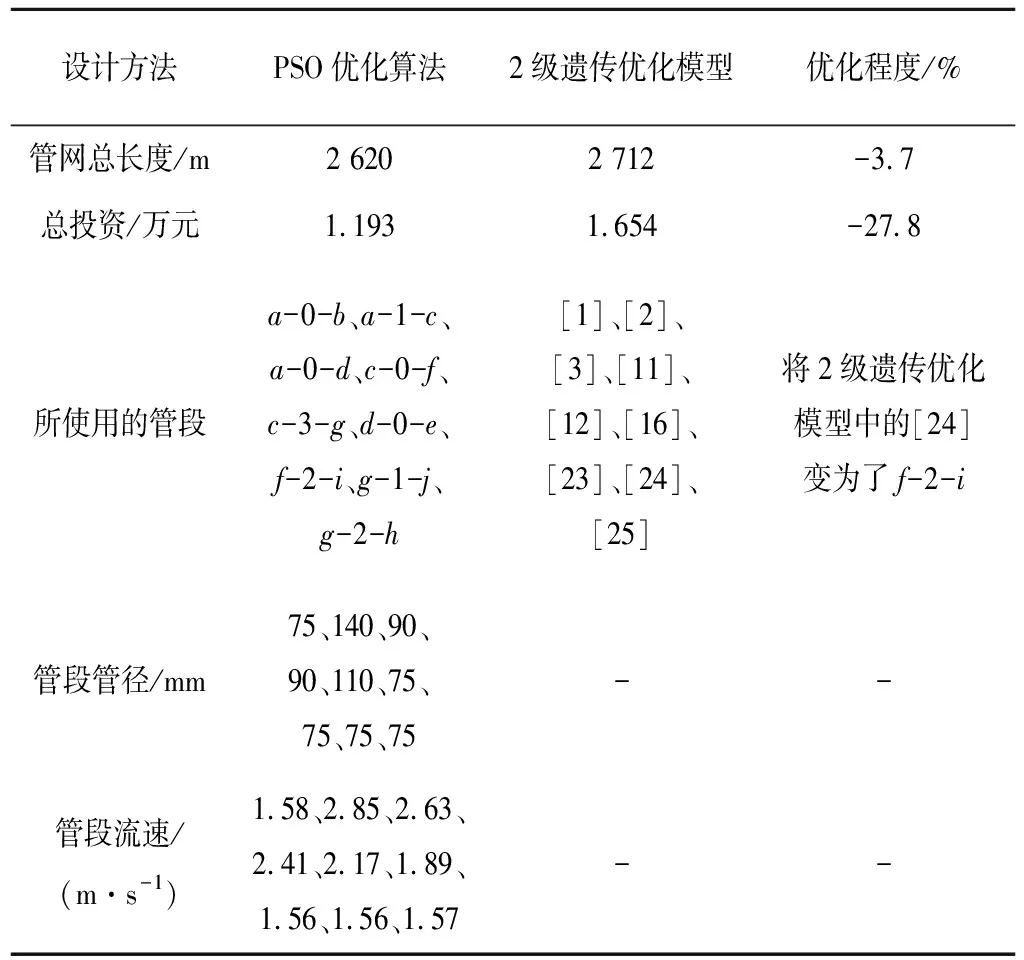
表4 灌溉管網優化布置對比

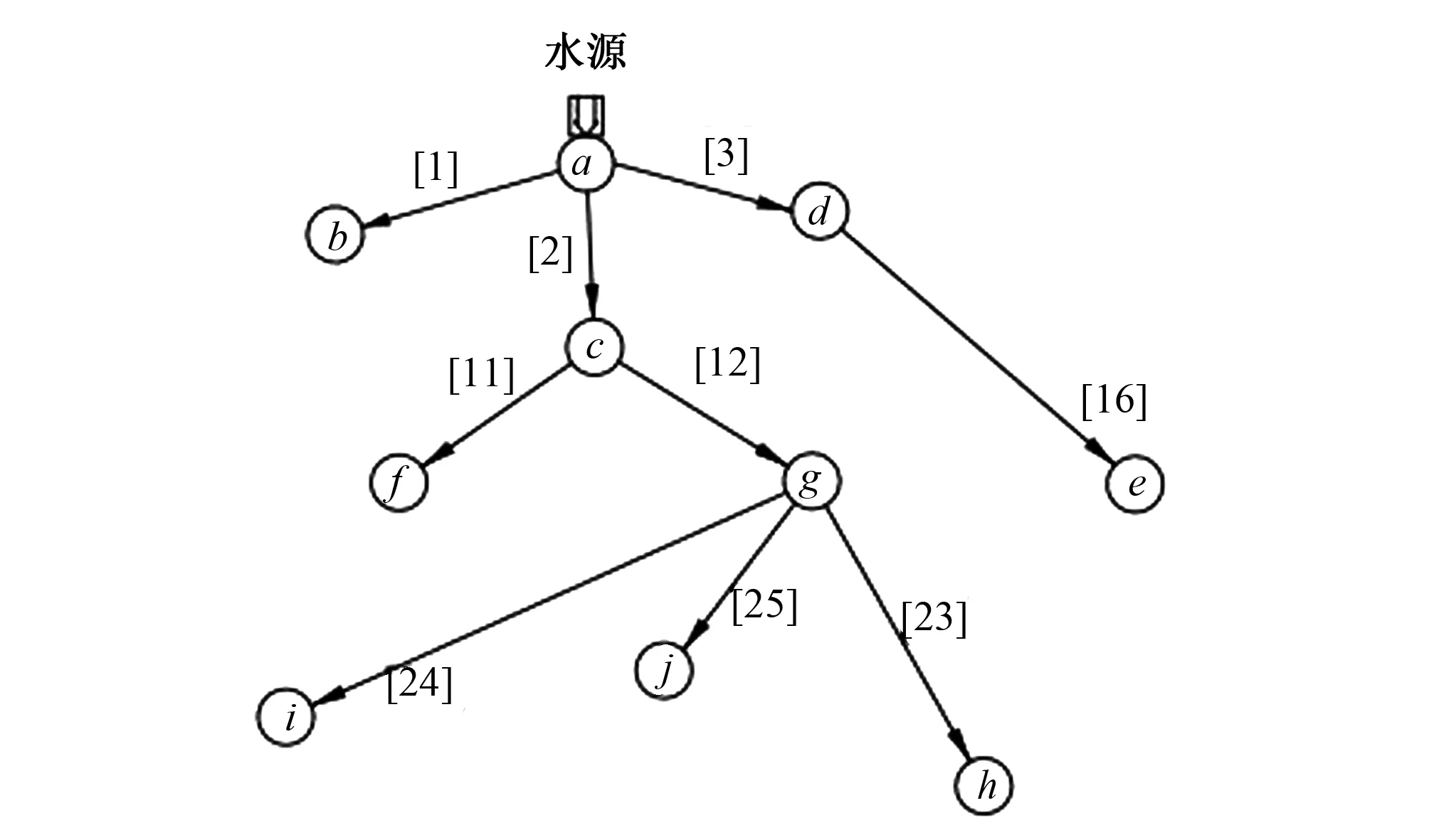
圖4 基于2級遺傳優化模型優化的灌區最優管網布置

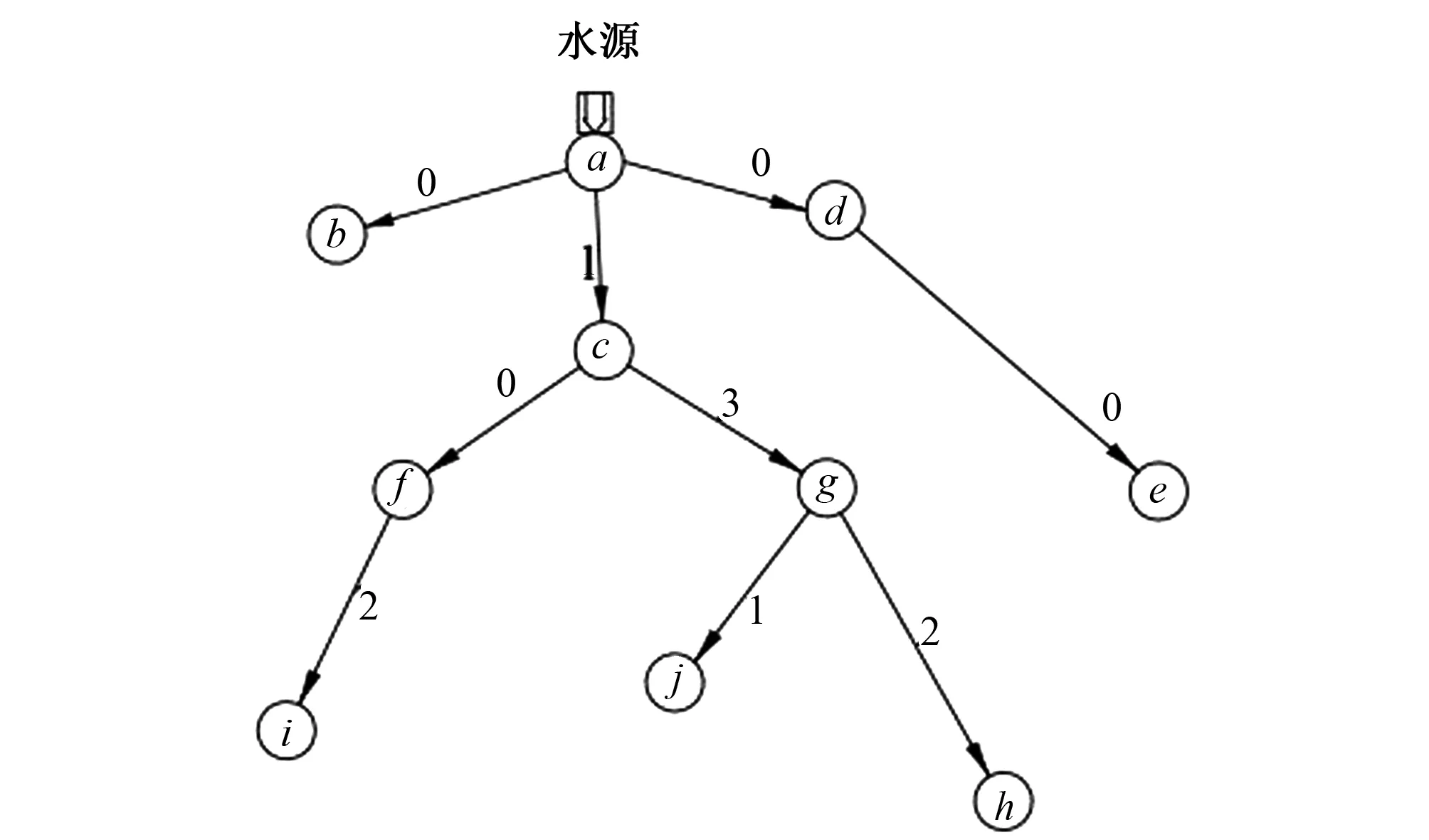
圖5 PSO算法優化的灌區最優管網布置

4 結 語

本文基于樹狀灌溉管網中單點供水的原則，將PSO優化算法與農田水利工程中的灌溉管網優化模型相結合，提出了基于PSO優化算法的樹狀灌溉管網優化模型。而后針對具體的實例對我國某灌區樹狀灌溉管網系統進行優化，得到了最終的優化方案。與2級遺傳優化模型得到的方案相比，使用該優化算法得到的最優管網布置的復雜度最小，需要的管網長度最小，投資成本最低，同時也能夠滿足灌區實際灌溉需求。本研究為PSO算法在灌溉管網優化布置中的應用提供了參考依據。

：

[1] 付玉娟,蔡煥杰. 灌溉管網優化研究現狀與展望[J].西北農林科技大學學報(自然科學版),2005,33(11):137-140.

[2] 付玉娟. 基于GIS的灌溉輸配水管網優化研究[D]. 陜西楊凌:西北農林科技大學,2008.

[3] 馬朋輝. 灌區微灌獨立管網系統優化設計研究[D]. 陜西楊凌：西北農林科技大學,2016.

[4] 王 昕,馬海燕,張 禾.等 規模化管道輸水灌溉管網優化模型研究與應用[J].節水灌溉,2015,(10):87-89.

[5] 胡良明,李 仟,鄭佩佩. 基于遺傳算法的農村供水管網優化設計[J].人民黃河,2017,39(1):102-105.

[6] 周榮敏,雷延峰. 管網最優化理論與技術[M].鄭州:黃河水利出版社,2002.

[7] 付玉娟,蔡煥杰,張旭東. 基于遺傳算法的樹狀灌溉管網優化設計[J].人民黃河,2006,28(7):42-44.

[8] 馬雪琴,呂宏興,朱德蘭. 基于遺傳算法的樹狀灌溉管網優化設計[J].中國農村水利水電,2013,(4):50-52.

[9] Goldberg D E,Kuo C H. Genetic algorithms in pipeline optimization[J].Journal of Computing in Civil Engineering,1985,1(2):128-141.

[10] 胡杰華,馬孝義,姚慰煒. 基于最小生成樹模型的樹狀灌溉管網的優化設計[J].中國農村水利水電,2012,(2):1-3.

[11] 李密青,鄭金華,羅 彪. 一種基于最小生成樹的多目標進化算法[J].計算機研究與發展,2009,46(5):803-813.

[12] 劉建華. 粒子群算法的基本理論及其改進研究[D].長沙：中南大學,2009.

[13] 蔡昌新. 粒子群算法在油田管網優化中的應用[J].長江大學學報(自然科學版：理工卷),2010,7(3):80-82,737.

[14] 柯文奇. 基于粒子群算法原油集輸管網優化[J].石油規劃設計,2010,21(1):15-17,50.

[15] 黃 晶. 基于粒子群算法的油田注水管網優化研究[D]. 黑龍江大慶市：大慶石油學院,2009.

[16] 薛英文,文倩倩. 基于粒子群算法的污水管網優化設計[J].中國農村水利水電,2010,(8):40-42.

[17] 俞雋亞,王增平,孫 潔. 基于支路交換----粒子群算法的配電網故障恢復[J].電力系統保護與控制,2014,42(13): 95-99.

[18] 張君則,艾 欣. 基于粒子群算法的多類型分布式電源并網位置與運行出力綜合優化算法[J].電網技術,2014,38(12):3 372-3 377.

[19] Mehdinejad M,Mohammadi-Ivatloo B,Dadashzadeh-Bonab R. Solution of optimal reactive power dispatch of power systems using hybrid particle swarm optimization and imperialist competitive algorithms[J].International Journal of Electrical Power & Energy Systems,2016,83:104-116.