半橢圓斷面渠道的水躍方程及其解法

馬子普，李書霞，郭曉明，趙蘇磊

(1.黃河水利委員會黃河水利科學研究院，鄭州 450003；2. 水利部堤防安全與病害防治工程技術研究中心，鄭州 450003;3.中國水利水電科學研究院，北京 100038)

迄今為止，除矩形外，不同專家學者已經得到了諸如梯形[1-4]、圓形[3-5,12]、三角形[6-9]、拋物線類[10,11]、馬蹄形[12,13]、蛋形[14]、U形[12,15]等多種不同的常見斷面形式的水躍方程，其相應的求解方法也多種多樣，常見的有公式擬合法、試算法、迭代法、圖解法等。與U形斷面渠道在國內干旱半干旱區的大規模推廣不同，預制混凝土半橢圓形渠道由于造價低、土地利用率低、便于運行維護，在國外大型農田灌溉網絡中得到了推廣應用[16]。水躍共軛水深作為為渠道水力設計的重要參數，目前并未有關于半橢圓斷面水躍方程及其解法的文獻，亟需推求其水躍方程并找到快速有效的解法。

半橢圓斷面水躍方程的共軛水深，不僅對躍前水深范圍有要求，躍前水深須大于臨界水深，同時躍后水深范圍也有要求，其躍后水深須不大于橢圓的垂向半徑，這意味著其躍前水深的范圍上下兩端均受到了限制，這是其不同于其他常見幾何形式的明渠水躍方程共軛水深的特點。為找到半橢圓斷面共軛水深的解法，首先推導出半橢圓斷面的水躍方程，接著重點確定了躍前水深的取值范圍，這是進行躍前水深與躍后水深二者關系分析的前提。最后通過大量計算繪制了無量綱躍前水深與無量綱躍后水深的關系圖，應用該關系圖可快速得到半橢圓斷面的共軛水深。

1 斷面水力要素與水躍方程推求

半橢圓斷面(見圖1)的幾何方程可表示為：

(1)

(2)

過水斷面面積為：

(3)

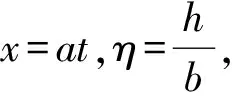
(4)

對于過水斷面形心到水面的距離hc，采用如下步驟計算：

(5)

(6)

(7)

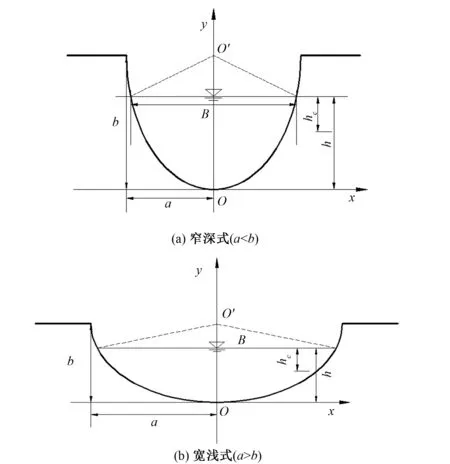
圖1 半橢圓斷面示意圖Fig.1 Sketch maps of semielliptical channel cross-sections

棱柱體水平明渠的水躍方程為:

(8)

式中：α為動量修正系數；Q為流量；g為重力加速度，通常取9.81 m/s2；A1、A2分別為水躍前、后過水斷面面積；hc1、hc2分別為水躍前、后過水斷面形心距水面的距離。

以窄深式半橢圓渠道中的水躍(見圖2)為例來推求水躍方程。

(9)

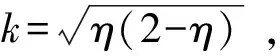
(10)

則無量綱水躍函數J′為：

(11)

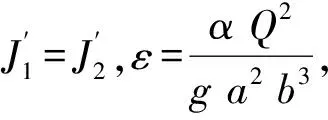
(12)

2 無量綱參數分析

欲分析η1與η2(即k1與k2)的關系，需首先分析ε及η1的取值范圍。

分析無量綱流量ε的取值范圍。

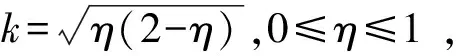
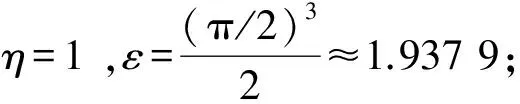
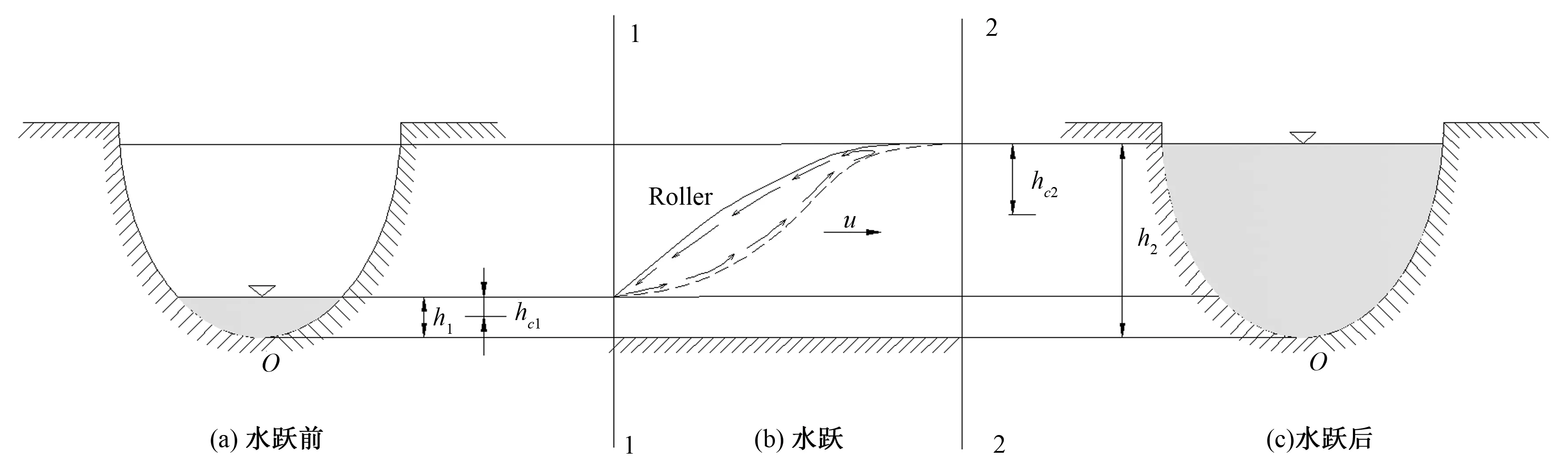
圖2 半橢圓斷面中的水躍示意圖(窄深式)Fig.2. Definition sketch map of hydraulic jump in a semielliptical channel(Narrow type)

(13)

(14)

(15)

(16)

再分析無量綱躍前水深η1的取值范圍。

對于躍前水深h1應滿足h1min≤h1≤hk，其中h1min為h2=b時所對應的躍前水深，hk為同流量下所對應的臨界水深。換成無量綱形式，即η1min≤η1≤ηk。

半橢圓形斷面的無量綱臨界水深方程為：

(17)

文獻[16]通過對該方程的擬合得到無量綱臨界水深 的近似計算式為：

(18)

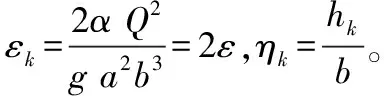
根據文獻[16]中的半橢圓斷面臨界水深計算公式計算臨界水深，并計算η2=1時所對應的η1min，可得到不同ε時所對應的η1的取值范圍(見圖3)。

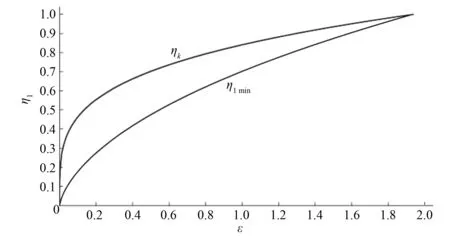
圖3 不同ε時η1的取值范圍 Fig.3 The depth range of η1 for different values of ε

在曲線ηmin與ηk之間的部分即為η1的合理取值范圍。

3 共軛水深的計算

共軛水深需根據式(12)計算。為清晰展示η2～η1的關系，針對不同的ε計算了大量不同η1(η1min≤η1≤ηk)所對應的η2，而后繪制了可描述半橢圓斷面的無量綱共軛水深關系圖(見圖4)：

圖4 無量綱共軛水深η2～η1關系圖Fig.4 The relationship map of dimensionless conjugate depth η2～η1

根據圖4 ，不同ε值時半橢圓斷面的η1所對應的η2，以及η2所對應的η1均可查到或通過插值快速得到。

4 應用實例

一半橢圓形斷面的形狀參數a=0.52 m，b=0.64m。若h1=0.2 m，試分別判定Q=0.25，0.5， 1 m3/s時，是否可能發生水躍，若可能發生則計算h2。

解法:(1)Q=0.25， 0.5， 1 m3/s，分別計算對應的無量綱流量ε，得ε=0.180、0.719、2.876，因2.876>1.937 9， 故Q=1 m3/s時水躍不會發生在半橢圓斷面渠道中。

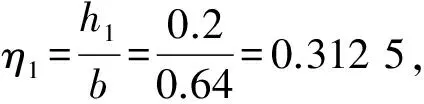
(3)ε=0.180，η1=0.312 5，可從圖4獲得無量綱躍后水深η2=0.87，則h2≈0.557。

5 結 語

基于半橢圓斷面的幾何特點推導了其無量綱水躍方程，接著深入分析了水躍方程中無量綱流量及躍前水深的取值范圍，并在此基礎上通過大量的計算繪制出了無量綱躍前水深與無量綱躍后水深的關系圖。依據共軛水深關系圖可快速得到針對半橢圓斷面的共軛水深值，并通過實例展示了該方法的應用過程。該方法簡便直觀，足以滿足水利工程設計的精度需要。

□

參考文獻：

[1] Asuquo E Eyo. Model for dredging a horizontal trapezoidal open channel with hydraulic jump [J].Journal of Mathematics Research,2012,4(3):132-141.

[2] JL Liu, ZZ Wang, X Fang. Computing conjugate depths in trapezoidal channels[J]. Proceeding of the Institution of Civil Engineers-Water Management,2012,165(9):507-512.

[3] Mitchell SB. Positive surge in trapezoidal and circular channels[J]. Proceeding of the Institution of Civil Engineers-Water Management,2010,163(4):199-205.

[4] Mitchell SB. Hydraulic jumps in trapezoidal and circular channels[J].Proceeding of the Institution of Civil Engineers-Water Management,2008,161(3):161-167.

[5] Mohd Jamil, Suhail A Khan. Theoretical study of hydraulic jump in circular channel section[J]. ISH Journal of Hydraulic Engineering,2010,16(1):1-10.

[6] I M H Rashwan. Analytical solution to problems of hydraulic jump in horizontal triangular channels[J].Ain Shams Engineering Journal,2013,(4)3:365-368.

[7] Vatankhah, Ali R, Omid, M H. Direct solution to problems of hydraulic jump in horizontal triangular channels[J].Applied Mathematics Letters,2010,23(9):1 104-1 108.

[8] Mahmoud Debabeche, Sonia Cherhabil, Amin Hafnaoui, et al. Hydraulic jump in a sloped triangular channel[J].Canadian Journal of Civil Engineering,2009,36(4):655-658.

[9] AE Eyo.Flow in a triangular open channel with hydraulic jump[J].Journal of the Nigerian Association of Mathematical Physics,2009,15(1):123-132.

[10] 代述兵，劉韓生，楊吉健. 三種拋物線形渠道共軛水深的顯式計算公式 [J].長江科學院院報,2015,32(8):51-56.

[11] Ma ZP, Zhang GG, Zhao CL, et al. Iterative algorithm of conjugate depth for parabolic channels[J]. Flow Measurement and Instrumentation, 2013,32(1):1-4.

[12] 馬吉明,謝省宗,梁元博. 城門洞形及馬蹄形輸入隧洞內的水躍[J].水利學報,2000,(7):20-24.

[13] 李若冰，張志昌. 標準Ⅰ型馬蹄形斷面水躍共軛水深的計算[J].西北農林科技大學學報(自然科學版), 2012,40(8):230-234.

[14] 張志昌，賈 斌，李若冰. 六圓弧蛋形斷面共軛水深計算方法的研究[J].西北農林科技大學學報(自然科學版), 2015,43(1):220-228.

[15] 張志昌，李若冰. U形渠道臨界水深、弗勞德數和水躍的研究[J].西安理工大學學報,2012,28(2):198-203.

[16] Vatankhah, Ali R. Critical and normal depths in semielliptical channels[J].ASCE Journal of Irrigation and Drainage Engineering, 2015,141(10):06015002.