具有有限X-余分解維數(shù)的模的上同調(diào)性質(zhì)
張翠萍,王鵬飛
(西北師范大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,甘肅 蘭州 730070)
0 引言
1969年,Auslander等[1]在雙邊Noether環(huán)R上引入了有限生成模M的Gorenstein 維數(shù)G-dimRM,并證明了G-dimRM≤pdRM(當(dāng)pdRM<∞時(shí),等號(hào)成立).他們還證明了廣義Auslander-Buchshaum公式.1995年,Enochs等[2]在任意環(huán)R上引入了Gorenstein投射模和Gorenstein投射維數(shù)GpdRM的概念,并研究了這類模的相關(guān)同調(diào)性質(zhì).稱左R模M是Gorenstein投射的,如果存在一個(gè)HomR(-,Q)正合的正合列…→P1→P0→P0→P1→…,使得M?Ker(P0→P0),其中Q,Pi(i=0,1…)是投射左R-模.記GpdRM=inf{n∈Z|存在正合列0→Gn→Gn-1→…→G1→G0→M→0,Gi是Gorenstein投射模,i=0,1,2,…,n}.如果這種正合列不存在,則規(guī)定GpdRM=∞.2010年,Bennis等[3]引入了X-Gorenstein投射模的概念;2014年,Zhu[4]引入了Abel范疇的擬可解子范疇X的概念,并給出了X-投射維數(shù)有限的模的幾種等價(jià)條件.隨著X的不同選取,X-Gorenstein投射模涵蓋了Gorenstein投射模[2]、Ding 投射模[5]和Gorenstein-AC投射模.2014年,Emmanouit等[6]給出了Gorenstein投射維數(shù)有限的模的幾種等價(jià)條件,利用這些條件研究了有有限Gorenstein投射維數(shù)的模相對(duì)于有有限投射維數(shù)的模的穩(wěn)定性以及相對(duì)于Gorenstein投射模的穩(wěn)定性.受此啟發(fā),對(duì)于模類X和W,文引入X-余分解維數(shù)和W-余分解維數(shù)的概念,給出了左R-模M的X-余分解維數(shù)有限的幾種等價(jià)刻畫,并研究了這類模相對(duì)于有有限W-余分解維數(shù)的模的穩(wěn)定性以及相對(duì)于模類X的穩(wěn)定性.
以下R指有單位元的結(jié)合環(huán),模指左R-模.
1 模的X-余分解維數(shù)
本節(jié)主要介紹與本文相關(guān)的一些定義和結(jié)論.
定義1設(shè)X是R-模類,稱X是余可解模類,如果滿足下列條件:
(1)X關(guān)于擴(kuò)張封閉,即對(duì)任意R-模的短正合列0→A→B→C→0,若A,C∈X,則B∈X.
(2)X關(guān)于單同態(tài)余核封閉,即對(duì)任意R-模的短正合列0→A→B→C→0,若A,B∈X,則C∈X.
(3)X關(guān)于有限直和與直和項(xiàng)封閉.
定義2設(shè)W是X的一個(gè)子類.稱W是X的投射生成子,如果下列條件滿足:
(1)對(duì)于任意X∈X,存在R-模短正合列0→X′ →W→X→0,其中W∈W,X′∈X.

(3)W關(guān)于有限直和封閉.
定義3設(shè)X是余可解模類,M是R-模.稱正合列
0→M→X0→X1→…→Xn-1→Xn→…
為M的X-余分解,其中Xi∈X(i=0,1,2,…).M的X-余分解維數(shù)(記為X-coresdimRM)定義為:X-coresdimRM=inf{n∈Z|存在正合列0→M→X0→X1→…→Xn-1→Xn→0,Xi∈X,i=0,1,2,…,n}.如果這種余分解不存在,則規(guī)定X-coresdimRM=∞.
類似地,可以定義M的W-余分解及其維數(shù).
以下X指余可解R-模類,W指X的投射生成子類.
命題1設(shè)n是非負(fù)整數(shù),則對(duì)任意的R-模M,以下結(jié)論等價(jià):
(1)X-coresdimRM≤n.
(2)存在R-模短正合列0→M→X→W→0,其中W-coresdimRW≤n-1,X∈X.
(3)存在R-模短正合列0→X→W′→M→0,其中W-coresdimRW′≤n,X∈X.

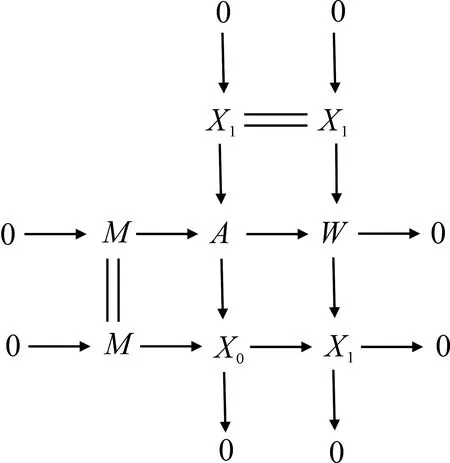
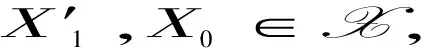

由上圖第二行短正合列知W-coresdimRM′≤n-1.最后考慮以下拉回圖:
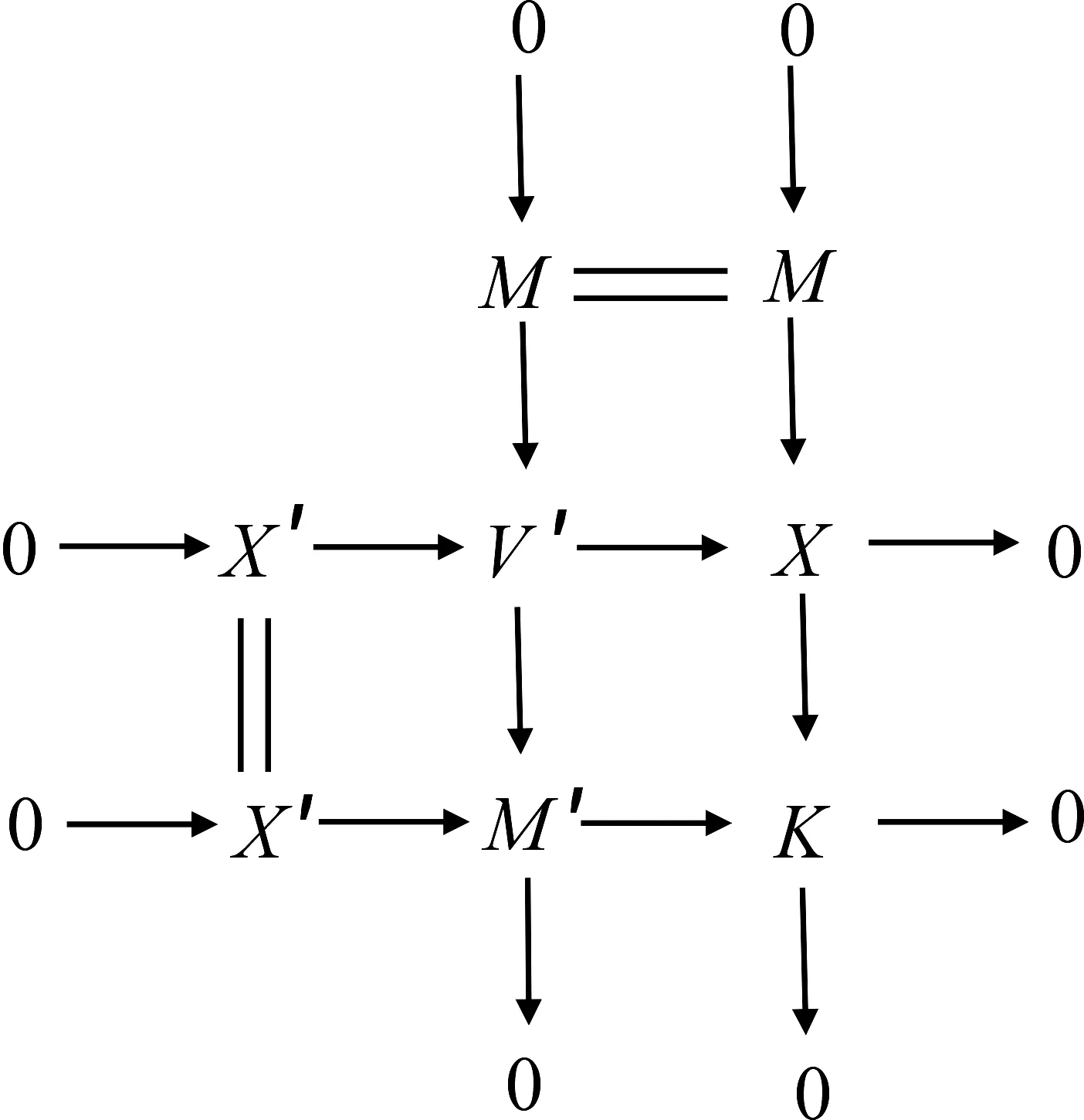
因?yàn)閄′,X∈X,從而V′∈X,故第二列即為所需短正合列.
(2)?(1).顯然.
(2)?(3).假設(shè)存在短正合列0→M→X→W→0,其中X∈X,W-coresdimRW≤n-1.因?yàn)閃是X的投射生成子類,故存在短正合列0→X′→W′→X→0,其中X′∈X,W′∈W.考慮以下拉回圖:

因?yàn)閃-coresdimRW≤n-1,因此W-coresdimRM′≤n,第一列即為所需短正合列.
(3)?(2).假設(shè)存在短正合列0→X″→W′→M→0,其中W-coresdimRW′≤n,X″∈X.由W-coresdimRW′≤n可知,存在短正合列0→W′→X→W″→0,其中W-coresdimRW″≤n-1,X∈W.考慮以下推出圖:

因?yàn)閄″,X∈X,從而M′∈X,故第三列即為所需短正合列. 】
命題2設(shè)R-模M的X-余分解維數(shù)有限.
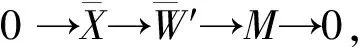

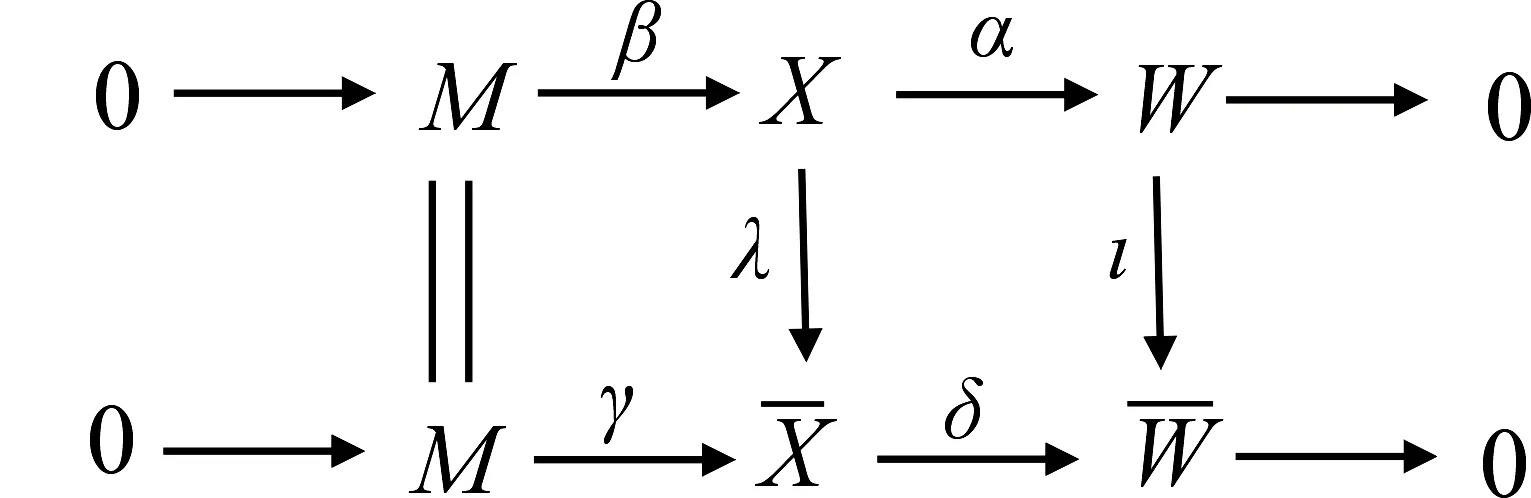
同理,存在λ′,ι′使下圖交換:

考慮以下交換圖:
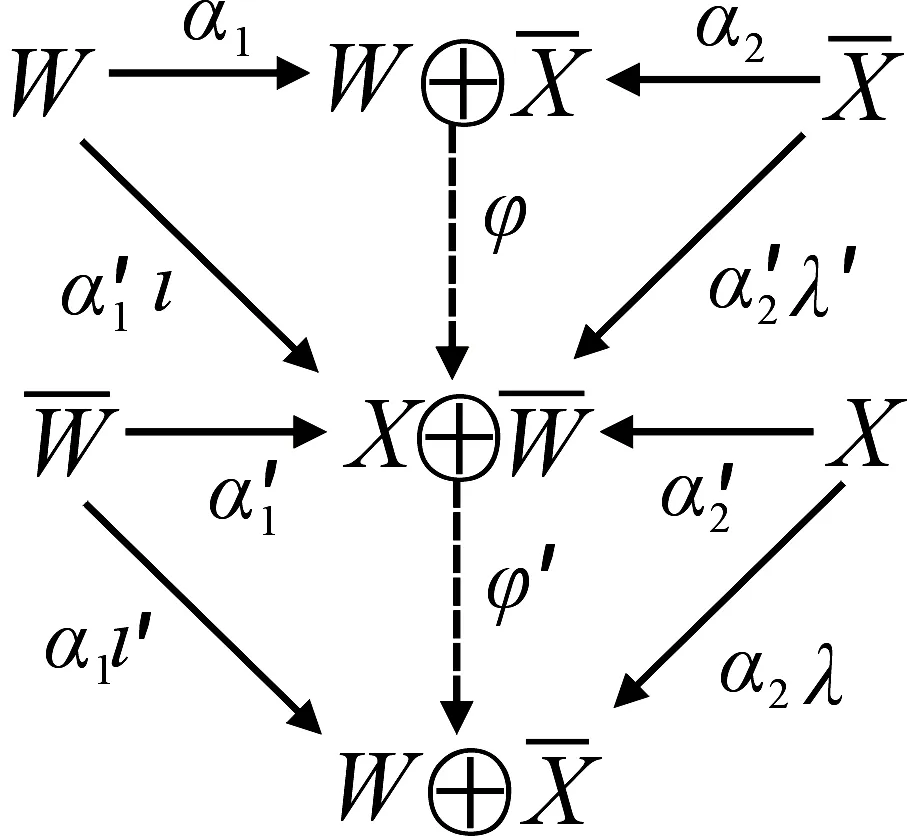

(2)證明與(1)類似. 】
