汽車自動變速器行星輪系公式原理推導
李曉宇 關崴 周章遐 趙彥輝 張海俠
哈爾濱東安汽車發動機制造有限公司技術中心 黑龍江省哈爾濱市 150060
1 引言
目前汽車自動變速器所采用的行星齒輪機構的類型主要有兩類:單行星輪系結構和雙行星輪系結構;其中比較有代表性的結構組合形式有:辛普森式和拉維納式行星齒輪機構,見圖1和圖2。
辛普森式行星齒輪機構是由兩個簡單的單行星輪的齒輪機構組合,而拉維納式行星齒輪機構是由一個單行星輪系和一個雙行星輪系組合而成,其中雙行星輪系中行星輪又分為長、短行星輪。

圖1 辛普森式行星輪系結構簡圖

圖2 辛普森式行星輪系結構簡圖
2 應用原理
2.1 單級行星輪系
對于行星輪系,由于行星架上的行星齒輪存在圍繞自身軸線的自轉和圍繞太陽輪軸線的公轉,所以機構的速比,不能直接引用定軸輪系齒輪速比的方式來計算。以下將介紹兩種方法,對行星輪速速比計算進行分析和總結。
2.1.1 轉化機構法—應用運動關系進行分析:
為計算速比,我們可以將模型進行簡化。即假設給整個輪系加上一個與行星架的轉速大小相等,轉向相反的附加轉速“ ”。根據相對運動關系,此時整個輪系中各原件間的相對運動關系并不發生變化。但此時行星輪架轉速為零。即原來運動的行星輪架轉化為靜止。這樣原來的行星輪系就轉化為一個假象的定軸輪系。對于此轉化機構的速比,則可以按定軸輪系的速比計算方式進行計算。也可以間接求出行星輪系的速比。
轉化方式:給整個機構設定一個轉速 使行星架相對靜止狀態 ,此時各構件之間的相對運動關系不變,此轉換輪系是個假想的定軸輪系。(見表1)
則轉化定軸輪系為:

圖3 單級行星輪系機構示意圖

表1 轉化前、后行星輪系中各構件的轉速
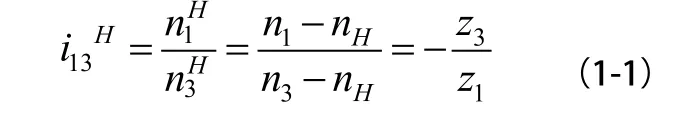
“-”負號代表在轉化輪系齒輪1、3轉向方向相反。
通用公式為:

式中:k為齒輪m至n轉之間外嚙合的次數。
輪系存在三個自由度即nm、nn、nh三個量,已知任意兩個量,即可知第三量數值;其中需假定某一轉向為正,相反方向則用負值計算。
將公式(1-1)進行轉化:

n1為太陽輪轉速;n3為齒圈轉速;nH為行星架轉速;Z1太陽輪齒數;Z2外齒圈齒數;
2.2.2 受力與能量分析法:
根據能量守恒定律,輸入和輸出功率相等代數和恒等于零:

式中:n1、n2、n3,M1、M2、M3分別是太陽輪、行星架、齒圈的轉速和力矩;
則作用在太陽輪、行星架、齒圈的力矩分別為:

又知行星齒輪機構參數λ為齒圈齒數Z2與太陽輪齒數Z1之比,


單級行星輪系運動特性方程為:

2.2 辛普森式行星輪系
通過圖1.1對零件進行拆分,可以得到兩個單級行星輪系;其中前行星架和后齒圈為組件,所以轉速相同,在計算過程中可以得到簡化。為更好理解,以下進行舉例說明。
根據單級行星輪系公式可知:

2.3 單排雙行星輪系結構
單排雙行星輪系因其結構復雜,運動關系相對較難理解,對于運動規律和各檔位的速比計算成為了一個難點,較難熟練計算。已下將推導出采用拉維納式行星輪系變速箱中的單排雙行星齒輪機構的運動特性方程。

圖4 單排雙行星齒輪輪系示意圖
與之前推導單排行星輪系方式相同,首先采用機構轉化法進行分析:
2.3.1 應用轉化機構法的公式,通用公式:

單排雙行星齒輪輪系運動特性公式:


式中: 、 、 分別是太陽輪、外齒圈、行星架的轉速, 、 分別是太陽輪、齒圈的齒數;
2.3.2 受力與能量分析法推導:

圖5 單排雙行星齒輪輪系受力示意圖
根據能量守恒定律,輸入和輸出功率相等代數和恒等于零:

式中: 、 、 分別是太陽輪、齒圈、行星架的轉速。
行星輪4和行星輪5分別與太陽輪1和齒圈2相嚙合,在它們中間起著中間輪的作用。設作用于太陽輪、齒圈、行星架的力矩分別為、、;

式中: 、 、、分別是太陽輪1、齒圈2、行星輪4、行星輪5的齒輪的節圓半徑。

又知行星齒輪機構參數 為齒圈齒數 與太陽輪齒數 之比,

將公式(3-6)、(3-7)、(3-8)代入(3-3)中可得太陽輪、齒圈和行星架的力矩:

3、綜上所述,由方法1和方法2得出結果相同;所以拉維納式行星齒輪機構是由1個單級行星齒輪式行星排和1個單排雙行星齒輪式行星排組合而成。將運動特性方程(1-3)和(3-1)組合即是拉維納式自動變速器行星齒輪輪系的運動特性公式:
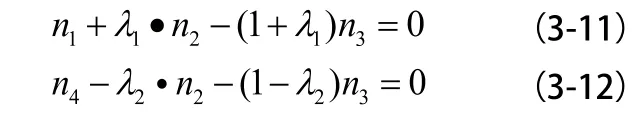
式中: 、 、 分別是前排(大)太陽輪、齒圈、行星架、后排(小)太陽輪的轉速。
公式(3-11)適用單級行星輪系,公式(3-12)適用單排雙行星齒輪輪系。
3 結語
目前汽車行業普遍裝用自動變速器,而汽車自動變速器中以行星輪系為多,一般行星輪系都屬于單排行星輪系、單排雙行星輪系這兩種行星輪系的變化相互部件連接得來,以上的運動特性方程的推導涉及行星傳動的運動學、動力學、物理學相關知識,通過結構示意圖淺顯易懂的對行星輪系運動特性進行分析,得出的運動特性方程能夠方便并且高效的為初學者,提供一種快速分析和計算行星輪系的公式及方法。

