含風(fēng)電的電力系統(tǒng)動(dòng)態(tài)經(jīng)濟(jì)調(diào)度研究＊

翟帥華，李 萍，顏 杰，王海峰，蔡 楠

（寧夏大學(xué)物理與電子電氣工程學(xué)院，寧夏銀川750021）

1 引言

隨著環(huán)境污染問題的日趨嚴(yán)重，能源問題受到了人們廣泛的關(guān)注，人們開始把目光投向了新能源領(lǐng)域。新能源通常包括太陽能、風(fēng)能、地?zé)崮堋淠艿取ｏL(fēng)力發(fā)電是開發(fā)利用程度很高的可再生能源，它在減輕環(huán)境污染、調(diào)整能源結(jié)構(gòu)等方面起著重要作用［1－2］。但隨著近年來風(fēng)力發(fā)電機(jī)裝機(jī)容量的迅速增加，越來越多的風(fēng)電需要并入大電網(wǎng)，這樣就面臨一個(gè)重要的問題，即大規(guī)模風(fēng)電并網(wǎng)情況下的電力系統(tǒng)安全、經(jīng)濟(jì)運(yùn)行問題。由于風(fēng)力具有很強(qiáng)的波動(dòng)性和隨機(jī)性，風(fēng)電是很不穩(wěn)定的，大量的風(fēng)電并入大電網(wǎng)之后，會(huì)對(duì)電力系統(tǒng)的安全穩(wěn)定造成巨大威脅，所以研究含風(fēng)電的電力系統(tǒng)動(dòng)態(tài)經(jīng)濟(jì)調(diào)度具有重要的意義。

目前，針對(duì)風(fēng)電的不確定性，含風(fēng)電場的電力系統(tǒng)動(dòng)態(tài)經(jīng)濟(jì)調(diào)度研究已經(jīng)有了大量研究。文獻(xiàn)［3］利用通用分布模型擬合不同風(fēng)電功率預(yù)測水平下的實(shí)際風(fēng)電功率分布，建立了考慮風(fēng)電低估、高估成本的日前動(dòng)態(tài)經(jīng)濟(jì)調(diào)度的隨機(jī)優(yōu)化模型，并用二次規(guī)劃算法與內(nèi)點(diǎn)法相結(jié)合的方式對(duì)模型求解。文獻(xiàn)［4］針對(duì)風(fēng)力的不確定性，基于可信性理論，用模糊參數(shù)的方式表示風(fēng)電和負(fù)荷預(yù)測值，最后將傳統(tǒng)確定性系統(tǒng)約束轉(zhuǎn)化成模糊機(jī)會(huì)約束，建立多時(shí)間尺度下含多模糊參數(shù)的模糊機(jī)會(huì)約束動(dòng)態(tài)經(jīng)濟(jì)調(diào)度模型。文獻(xiàn)［5］針對(duì)風(fēng)力的隨機(jī)性，設(shè)置了發(fā)電機(jī)的禁運(yùn)域，建立了含風(fēng)電場帶禁運(yùn)域的實(shí)時(shí)動(dòng)態(tài)經(jīng)濟(jì)調(diào)度模型。文獻(xiàn)［6］考慮火電機(jī)組的閥點(diǎn)效應(yīng)，并針對(duì)風(fēng)電的不確定性，采用魯棒性方法處理，最后提出了一種改進(jìn)教學(xué)算法與線性規(guī)劃相嵌套的求解方法。

本文建立了一種含風(fēng)電的電力系統(tǒng)動(dòng)態(tài)經(jīng)濟(jì)調(diào)度模型，在常規(guī)火電機(jī)組約束條件的基礎(chǔ)上，加入了系統(tǒng)正負(fù)旋轉(zhuǎn)備用容量，去平衡風(fēng)力發(fā)電不確定對(duì)電力系統(tǒng)的影響，并且利用改進(jìn)的算法對(duì)模型進(jìn)行優(yōu)化，最后通過算例仿真，驗(yàn)證模型的可行性及算法的有效性。

2 電力系統(tǒng)經(jīng)濟(jì)優(yōu)化調(diào)度模型

2.1 目標(biāo)函數(shù)

隨著國家對(duì)新能源發(fā)電并網(wǎng)的政策扶持，全額消納新能源發(fā)電就顯得越來越重要［7］。在研究含風(fēng)電的電力系統(tǒng)動(dòng)態(tài)經(jīng)濟(jì)調(diào)度時(shí)，忽略風(fēng)力發(fā)電的成本，在滿足系統(tǒng)安全約束條件的情況下，對(duì)常規(guī)火電機(jī)組進(jìn)行組合優(yōu)化，實(shí)現(xiàn)對(duì)風(fēng)電的全額消納，使系統(tǒng)的發(fā)電成本最優(yōu)［8-9］，具體目標(biāo)函數(shù)如下：

式中，ai、bi、ci為火電機(jī)組發(fā)電成本的參數(shù)。

2.2 約束條件

（1）忽略網(wǎng)損時(shí)的有功平衡約束

（2）機(jī)組出力約束

（3）機(jī)組最小啟動(dòng)/停止時(shí)間約束

（4）正負(fù)旋轉(zhuǎn)備用容量約束

對(duì)于含風(fēng)電并網(wǎng)的電力系統(tǒng)，為避免系統(tǒng)在運(yùn)行過程中負(fù)荷突然增加或發(fā)電機(jī)停電檢修等情況的出現(xiàn)，應(yīng)該為電力系統(tǒng)添加正、負(fù)旋轉(zhuǎn)備用，其正、負(fù)旋轉(zhuǎn)備用約束為：

3 優(yōu)化算法

3.1 粒子群優(yōu)化算法

粒子群優(yōu)化（PSO）算法是 Kennedy和Eberha等人在1995年提出的，算法起源于鳥群飛行覓食行為研究［10］。PSO優(yōu)化算法是隨機(jī)并行搜索的，具有設(shè)置參數(shù)少、結(jié)構(gòu)簡單、搜索速度快、魯棒性好等特點(diǎn)，對(duì)于解決非線性、多維變量、多峰值的復(fù)雜優(yōu)化問題非常有效。粒子群優(yōu)化算法首先在可行解區(qū)域生成一群粒子，每個(gè)粒子相當(dāng)于鳥群中的一個(gè)個(gè)體，該粒子所處的位置就是問題初始解，每個(gè)粒子的位置都是隨機(jī)產(chǎn)生的，并且粒子在飛行的過程中通過目標(biāo)函數(shù)確定一個(gè)適應(yīng)值，粒子根據(jù)個(gè)體極值和群體極值，不斷更新自身位置，最終達(dá)到最優(yōu)位置。其通過式（8）、式（9）更新自身的速度和位置。

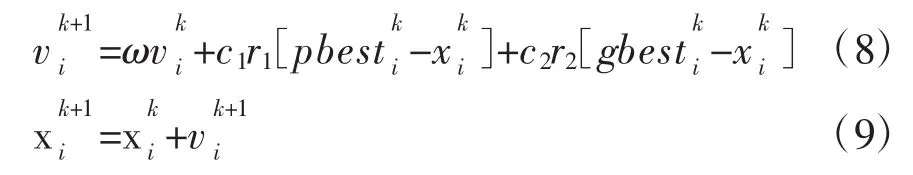
3.2 改進(jìn)的粒子群優(yōu)化算法

在優(yōu)化調(diào)度過程中，發(fā)現(xiàn)慣性權(quán)重對(duì)粒子算法有很大的影響。在迭代初期取較大的慣性權(quán)重，對(duì)于粒子的全局搜索較為有利，但不容易得到精確解；在迭代后期取較小的慣性權(quán)重，對(duì)于粒子的局部搜索較為有利，這樣可以避免粒子陷入局部極小值的情況，提高算法的搜索性能。本文引入線性慣性權(quán)重因子w改進(jìn)粒子群算法（Improved particle swarm optimization，簡稱IPSO算法），如式（10）所示。

式中，ωstart是初始慣性權(quán)重；ωend是迭代至最大次數(shù)時(shí)的慣性權(quán)重；k是當(dāng)前迭代次數(shù)；Kmax是最大迭代次數(shù)。

3.3 二次規(guī)劃算法

二次規(guī)劃（Quadratic programming-QP）是最優(yōu)化問題的一種特殊形式，其目標(biāo)函數(shù)是二次函數(shù)，約束條件是線性等式或不等式［11］。因?yàn)槎我?guī)劃算法相對(duì)比較簡單，容易求解，所以在許多領(lǐng)域有很多應(yīng)用，例如，在金融投資、建筑工程、航空航天、運(yùn)籌學(xué)、經(jīng)濟(jì)數(shù)學(xué)、管理科學(xué)、系統(tǒng)分析、組合優(yōu)化等方面都有廣泛應(yīng)用。二次規(guī)劃的一般形式如式（11）所示。

式中，x為n維向量；C和D分別是n維系數(shù)向量和正定矩陣；A和B分別是m×n維系數(shù)矩陣和m維常數(shù)向量；xmin、xmax分別是 x的上、下限值。

4 基于IPSO-QP算法的調(diào)度模型

4.1 IPSO-QP 算法

為了降低火電機(jī)組的運(yùn)行成本，在建立含風(fēng)電的電力系統(tǒng)動(dòng)態(tài)調(diào)度模型后，使用粒子算法與二次規(guī)劃算法相結(jié)合方式對(duì)模型進(jìn)行優(yōu)化。利用粒子群算法求出機(jī)組的初始開停狀態(tài)，用二次規(guī)劃算法求出機(jī)組安全約束條件下的各機(jī)組出力值，根據(jù)所有機(jī)組各時(shí)段的出力值求出粒子的適應(yīng)度值，然后判斷是否達(dá)到最大迭代次數(shù)，經(jīng)過不斷更新粒子的速度和位置，最終得到滿足約束條件的最小機(jī)組出力表。

4.2 優(yōu)化的步驟

（1）輸入機(jī)組、負(fù)荷和粒子群算法初始參數(shù)；

（2）利用粒子群算法求出初步的機(jī)組啟停計(jì)劃；

（3）開始迭代；

（4）利用粒子更新公式，更新粒子自身的速度和位置；

（5）求粒子的適應(yīng)度值，并記錄每個(gè)粒子的個(gè)體極值pbest及群體極值gbest。

（6）判斷是否達(dá)到迭代次數(shù)，如“否”，返回（4），如“是”，繼續(xù)下一步；

（7）輸出滿足約束條件的最優(yōu)的機(jī)組啟停計(jì)劃；

（8）用二次規(guī)劃算法求出最優(yōu)的機(jī)組出力分配。

5 算例仿真

為驗(yàn)證算法的有效性，以10臺(tái)常規(guī)火電機(jī)組和一個(gè)風(fēng)電場組成的系統(tǒng)為例，對(duì)算法的有效性進(jìn)行檢驗(yàn)。系統(tǒng)旋轉(zhuǎn)備用取系統(tǒng)負(fù)荷的5%，測試系統(tǒng)中的10機(jī)組，測試中假設(shè)風(fēng)電場的出力全部消納。IPSO參數(shù)的設(shè)置如下：慣性權(quán)重系數(shù)為ω，ωstart=0.9，ωend=0.4；加速常數(shù) c1=2，c2=2；種群規(guī)模N=40，迭代次數(shù)設(shè)為100次。各調(diào)度時(shí)段的負(fù)荷及各時(shí)段的風(fēng)電預(yù)測情況如圖1所示。

圖1 各時(shí)段的負(fù)荷與風(fēng)電的值

從圖1可以看出，一天中的風(fēng)電出力波動(dòng)是很大的，最大出力出現(xiàn)在夜里凌晨四點(diǎn)左右及晚上的6點(diǎn)到8點(diǎn)鐘。但負(fù)荷的最大值出現(xiàn)在中午12點(diǎn)和晚上的8點(diǎn)鐘。風(fēng)力的不確定性，使系統(tǒng)出現(xiàn)反調(diào)峰現(xiàn)象，如果應(yīng)對(duì)風(fēng)電不確定的旋轉(zhuǎn)備用選取不當(dāng)，會(huì)對(duì)系統(tǒng)的安全運(yùn)行造成影響。

表1 各時(shí)段10機(jī)組的出力表

在Matlab環(huán)境下，用改進(jìn)后的算法優(yōu)化經(jīng)濟(jì)調(diào)度模型，得到風(fēng)電并網(wǎng)之后最優(yōu)機(jī)組的出力分布情況如表1所示。改進(jìn)前的PSO-QP算法與改進(jìn)后的IPSO-QP算法對(duì)比情況見表2。

表2 算法改進(jìn)前后運(yùn)行成本對(duì)比

從表2中可以看出，對(duì)比PSO-QP算法，改進(jìn)后的優(yōu)化算法得到的機(jī)組的運(yùn)行成本減少了1240美元。

6 結(jié)束語

本文以火電機(jī)組的發(fā)電成本最小為目標(biāo)函數(shù)，建立了含風(fēng)電的電力系統(tǒng)動(dòng)態(tài)調(diào)度模型，并提出了改進(jìn)粒子群算法與二次規(guī)劃算法相結(jié)合的方式，對(duì)調(diào)度模型進(jìn)行調(diào)度優(yōu)化。優(yōu)化分為兩個(gè)過程，首先通過改進(jìn)的粒子群算法確定負(fù)荷變化時(shí)的機(jī)組啟停順序，然后利用二次規(guī)劃算法對(duì)負(fù)荷優(yōu)化分配，實(shí)現(xiàn)了發(fā)電計(jì)劃和備用容量優(yōu)化的協(xié)調(diào)，在保障系統(tǒng)安全的前提下，合理地安排火電機(jī)組的計(jì)劃出力，并在預(yù)留合適的備用容量的情況下，得到最小化的火電機(jī)組發(fā)電成本。最后，通過Matlab仿真驗(yàn)證了所建立的調(diào)度模型的合理性和改進(jìn)算法的有效性。