隨機變分不等式的隨機投影梯度算法

楊 燦, 夏福全

(四川師范大學 數學與軟件科學學院, 四川 成都 610066)

1 引言及預備知識

本文主要研究如下的隨機變分不等式問題:求x∈C使得

〈E[f(x,ξ(θ))],y-x〉≥0, ?y∈C,

(1)

其中,C是Rn中的非空閉凸子集,f(x,ξ):Rn×Rk→Rn是一個連續映射,ξ:Ω→Rk是定義在某概率空間(Ω,Λ,P)上的隨機變量,E[f(x,ξ(θ))]表示f(x,ξ(θ))相對于分布ξ的期望值.

眾所周知,變分不等式問題在交通、經濟平衡、博弈論和網絡問題等方面都有著重要應用[1-5].在實際生活中,雖然許多問題只涉及到確定的數據,但也有很多問題的數據包含隨機變量,比如幾個公司提供可替代商品的庫存和服務的價格競爭[6-7]、一些隨機動態博弈[8-9].很多包含隨機變量的問題都可以歸結為帶有隨機變量的變分不等式模型,即隨機變分不等式問題.隨機變分不等式問題是一般變分不等式問題的一個推廣[10-12],但關于隨機變分不等式的理論與算法都非常有限.由于隨機變分不等式有著廣泛的應用,因而,隨機變分不等式問題引起了越來越多的專家學者的關注和研究.

令F(x)=E[f(x,ξ(θ))],則(1)式變為下列的一般變分不等式問題:求x∈C滿足

〈F(x),y-x〉≥0, ?y∈C.

(2)

對于經典的變分不等式問題(2),已經有非常多的有效的方法可以求解.因此,當E[f(x,ξ(θ))]容易計算時,隨機變分不等式問題容易求解.但在實際應用中,E[f(x,ξ(θ))]的計算一般比較困難,比如雖然函數f(x,ξ(θ))已知,但是ξ的分布未知并且ξ的信息只能從過去樣本的數據中獲得;或者E[f(x,ξ(θ))]必須通過模擬近似估算而不能直接獲得.在這些情況下,已有求解一般變分不等式的數值方法等都不能直接用于求解隨機變分不等式問題.

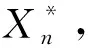
最近,Malitsky[26]提出了求解變分不等式問題(2)的一種新的數值方法——投影反射梯度算法,具體迭代過程是:

xn+1=PC(xn-λ(F(yn)),
yn=2xn-xn-1,

其中,PC表示在集合C上的投影,λ>0是常數.為了證明該算法所產生的迭代序列的收斂性,假設F是偽單調以及Lipschitz連續的.該算法的優點在于:在迭代的每一步,只需要向可行集進行一次投影,迭代中也只需對函數F賦值一次.數值結果表明該算法快速且有效.

本文主要的工作是結合Malitsky[26]的投影反射梯度算法和隨機逼近方法,給出了隨機變分不等式(1)的隨機投影梯度方法.該方法結合了Malitsky[26]算法和隨機逼近方法的優點,因而算法簡單快速.在一定條件下,證明了該算法所產生的迭代序列的全局收斂性.

定義1.1設C?Rn為非空閉凸集,對任意x∈Rn,定義

PC(x):=argmin{‖x-y‖:y∈C},

稱PC(x)是x在C上的投影.

定義1.2稱映射F:Rn→Rn是：

1) 單調的,若對于任意的x,y∈Rn,有

〈F(x)-F(y),x-y〉≥0;

2) 是偽單調的,若對于任意的x,y∈Rn,有

〈F(y),x-y〉≥0?〈F(x),x-y〉≥0;

3) 是偽單調-加的,若F是偽單調的,且對于任意的x,y∈Rn,有

〈F(x),x-y〉=0,〈F(y),x-y〉≥

0?F(x)=F(y);

4)Lipschitz連續的,若存在常數L>0,對于任意的x,y∈Rn,有

‖F(x)-F(y)‖≤L‖x-y‖.

引理1.1[27]設C是Rn中的非空閉凸集,對任意x∈Rn,則:

1) 〈PC(x)-x,y-PC(x)〉≥0,?y∈C;

2) ‖PC(x)-y‖2≤‖x-y‖2-‖x-PC(x)‖2,?y∈C.

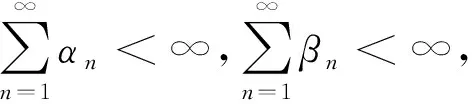
E[Vn+1|Fn]≤(1+αn)Vn-γn+βn,

(3)

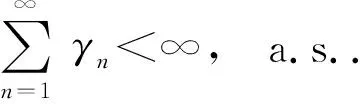
2 算法及其收斂性

總假設F(x)=E[f(x,ξ(θ))]且F是Lipschitz連續映射,其Lipschitz連續系數為L>0.對每個n≥0,令ωn=f(xn,ξn)-F(xn).對給定的常數λ>0,設

r(x,y):=‖y-PC(x-λF(y))‖+‖x-y‖.

首先介紹隨機變分不等式問題(2)解的迭代算法.

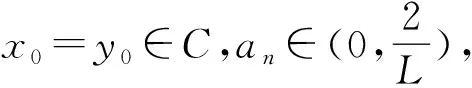
2) 對當前的迭代點xn和yn,令

xn+1=PC(xn-an(F(yn)+ωn)).

(4)

若r(xn,yn)=0,則算法停止.否則,計算

yn+1=2xn+1-xn；

(5)

3) 令n=n+1,回到2).

顯然,ωn=f(xn,ξn)-F(xn)是隨機誤差.易知,在迭代的第n步,用ξ的一個樣本ξn計算f(xn,ξn),并把它當作F(xn)的一個近似.因此,當近似F(xn)時,不需要知道變量ξ的概率分布.這非常有利于算法的實現.

對任意n≥1,首先定義與算法2.1相關的σ-域為

Fn=(w0,w1,…,wn-1,y0,y1,…yn-1,x0,x1,…xn}.

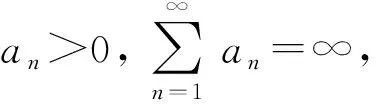
(b)E[ωn|Fn]=0;

易知,假設2.1中條件(a)是隨機逼近中選擇步長的一個準則,參見文獻[29].假設條件(b)和(c)表示隨機誤差ωn是無偏的且是受控的方差標度.這些假設是隨機逼近方法相關文獻中的常用準則.

引理2.1若變分不等式問題(1)的解集S非空,z∈S且F:Rn→Rn為Lipschitz連續映射,則由算法2.1所生成的序列{xn}和{yn}滿足

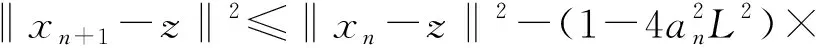
(6)

證明根據xn+1=PC(xn-an(F(yn)+wn))以及引理2.1的2)有

‖xn+1-z‖2≤‖xn-an(F(yn)+wn)-z‖2-
‖xn-an(F(yn)+wn)-xn+1‖2=
‖xn-z‖2-‖xn-xn+1‖2-
2an〈F(yn)+wn,xn-z〉+
2an〈F(yn)+wn,xn-xn+1〉=
‖xn-z‖2-‖xn-xn+1‖2-
2an〈F(yn)+wn,xn+1-z〉=
‖xn-z‖2-‖xn-xn+1‖2-
2an〈F(yn),xn+1-z〉-2an〈wn,xn+1-z〉.

(7)

易知

-2an〈F(yn),xn+1-z〉=

-2an〈F(yn)-F(yn-1),xn+1-yn〉-
2an〈F(yn-1),xn+1-yn〉-
2an〈F(yn),yn-z〉.

(8)

由于{xn}?C,根據

xn=PC(xn-1-an(F(yn-1)+wn-1))

以及引理1.1的1)有

〈xn-xn-1+an(F(yn-1)+wn-1,xn-xn+1〉≤0,
〈xn-xn-1+an(F(yn-1)+wn-1,xn-xn-1〉≤0.

上述兩式相加,注意到yn=2xn-xn-1,有

〈xn-xn-1+an(F(yn-1)+wn-1),yn-xn+1〉≤0.

從而,根據xn-xn-1=yn-xn及上式可推知

2an〈F(yn-1),yn-xn+1〉≤
2〈xn-xn-1,xn+1-yn〉+2an〈wn-1,xn+1-yn〉=
2〈yn-xn,xn+1-yn〉+2an〈wn-1,xn+1-yn〉=
‖xn+1-xn‖2-‖xn-yn‖2-
‖xn+1-yn‖2+2an〈wn-1,xn+1-yn〉.

(9)

另一方面,由于F是Lipschitz連續映射,則

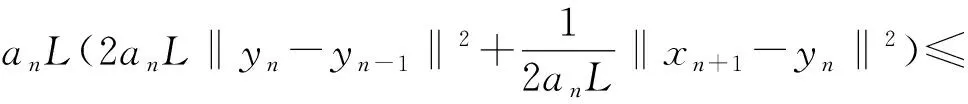
(10)

此外,根據Cauchy-Schwarz不等式及均值不等式,易知

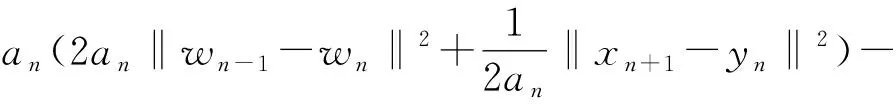
(11)

將(8)～(10)式代入(7)式得到

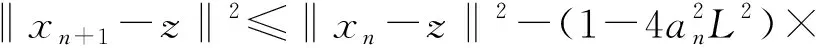
(12)

引理得證.

選取常數λ>0滿足下列不等式

事實上,由于an→0(n→∞),當n充分大時,可以選取充分大λ>0滿足(13)式.

引理2.2若變分不等式問題(1)的解集S非空,z∈S且F：Rn→Rn為Lipschitz連續映射,則由算法2.1所生成的序列{xn}和{yn}滿足

(14)

其中λ>0滿足(13)式.

證明設z∈S,選取λ>0滿足(13)式,根據F的Lipschitz連續性以及Cauchy-Schwarz不等式有

2an〈F(yn),yn-z〉=

〈F(yn)-F(xn),yn-z〉+2an〈F(xn),yn-z〉≥

-2anL‖yn-xn‖‖yn-z‖+2an〈F(xn),yn-z〉≥

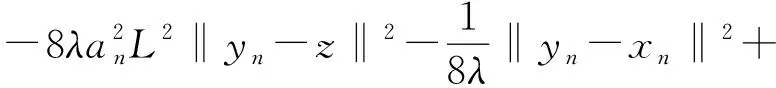
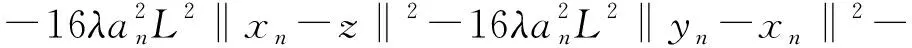
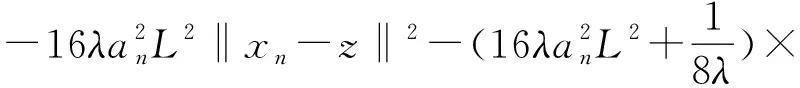
(15)

另一方面,根據F的Lipschitz連續性以及Cauchy-Schwarz不等式有

2an〈F(xn),yn-z〉=

2an〈F(xn),yn-xn〉+2an〈F(xn),xn-z〉=

2an〈F(xn)-F(yn),yn-xn〉+
2an〈F(yn),yn-xn〉+2an〈F(xn),xn-z〉≥
-2anL‖yn-xn‖-2an‖F(yn)‖×
‖yn-xn‖+2an〈F(xn),xn-z〉≥

-2anL‖yn-xn‖-2an‖F(yn)-F(z)‖×
‖yn-xn‖-2an‖F(z)‖‖yn-xn‖+
2an〈F(xn),xn-z〉≥-2anL‖yn-xn‖-
2anL‖yn-z‖‖yn-xn‖-
2an‖F(z)‖‖yn-xn‖+2an〈F(xn),xn-z〉≥

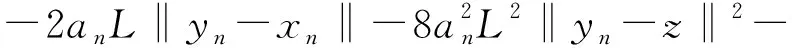
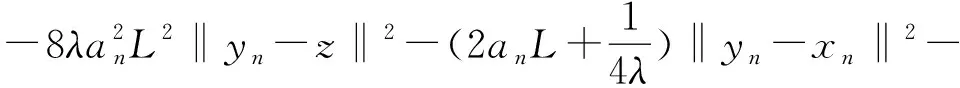
將(16)式代入(15)式可得(14)式,結論成立.

定理2.1假設變分不等式問題(1)的解集S非空,F：Rn→Rn為偽單調-加Lipschitz連續映射,則由算法2.1所生成的序列{xn}幾乎處處收斂于問題(1)的解.

證明對任意z∈S,λ>0滿足(13)式,根據引理2.1和引理2.2有

‖xn+1-z‖2≤

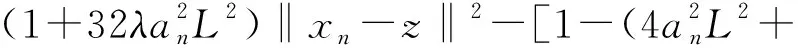
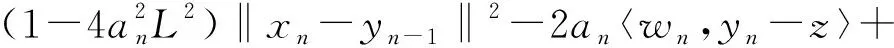
根據(17)式及假設條件2.1可得

E[‖xn+1-z‖2|Fn]≤

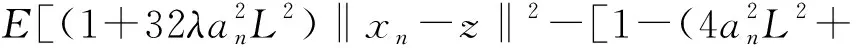
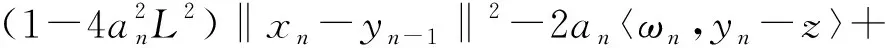
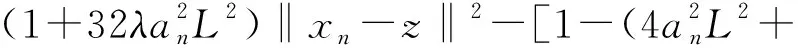
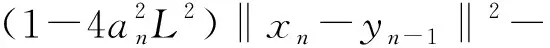
(18)

令

由假設條件2.1及(13)式可知,對充分大的n有,ξn>0,ηn>0,從而(18)式變為

E[‖xn+1-z‖2|Fn]≤

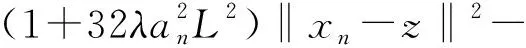
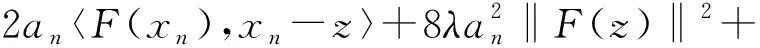
(19)

再設

γn=ξn‖xn-yn‖2+ηn‖xn-yn-1‖2+
2an〈F(xn),xn-z〉,

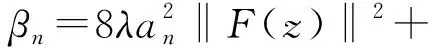
(20)

注意到z∈S是變分不等式(1)的解,xn∈C,故

〈F(xn),xn-z〉≥0.

(21)

另外,根據假設條件2.1及(13)式可知

(22)

從而根據(20)～(22)式可知

(23)

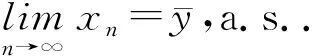
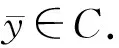
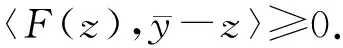
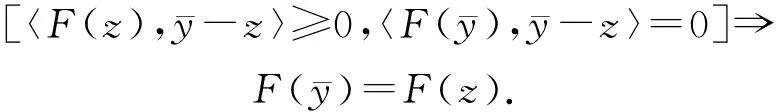
此外,對任意的y∈C,由于z∈S,有〈F(z),y-z〉≥0.因此,對任意的y∈C有

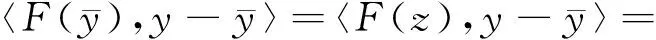
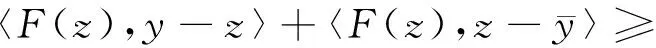
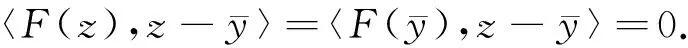
由于對任意x∈C,F(x)=E[f(x,ξ(θ))],故

〈E[f(x,ξ(θ))],y-x〉≥0, ?y∈C,

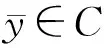
[1]BREZISH.Opérateursmaximauxmonotones:etsemi-groupesdecontractionsdanslesespacesdeHilbert[J].JAcousticalSocietyAmerica,1989,125(4):2680.

[2]GIANNESSIF,MaugeriA.VariationalInequalityandNetworkEquilibriumProblems[M].NewYork:PlenumPress,1995:315-320.

[3]VERMARU.Generalconvergenceanalysisfortwo-stepprojectionmethodsandapplicationtovariationalproblems[J].ApplMathLett,2005,18(11):1286-1292.

[4]FACCHINEIF,PANGJS.Finite-dimensionalVariationalInequalitiesandComplementaryProblemsVolumeI/II[M].NewYork:Springer-Verlag,2003.

[5]LUOZQ,PANGJS,RALPHD.MathematicalProgramswithEquilibriumConstraints[M].Cambridge:CambridgeUniversityPress,1996.

[6]CHENFY,YANH,YAOL.Anewsvendorpricinggame[J].IEEETransactionsonSystemsManandCyberneticsPartASystemsandHumans,2004,34(4):450-456.

[7]CMAHAIANS,VANRYZING.Inventorycompetitionunderdynamicconsumerchoice[J].OperationsResearch,2001,49(5):464-657.

[8]BASART,OLSDERG.DynamicNoncooperativeGameTheory[M].Philadeiphia:SIAM,1999.

[9]FILARJ,VRIEZEK.CompetitiveMarkovDecisionProcesses[M].Berlin：Springer-Verlag,1996.

[10]GURKANG, ?ZGEAY,ROBINSONSM,etal.Samplepathsolutionofstochasticvariationalinequalities,withapplicationstooptionpricing[C].Proceedingsofthe28thconferenceonWintersimulation-WSC96,1996.DOI:10.1145/256562.256646.

[11]GURKANG,OZGEAY,ROBINSONSM.Sample-pathsolutionofstochasticvariationalinequalities[J].MathematicalProgramming,1999,84(2):313-333.

[12]ROBINSONSM.Analysisofsample-pathoptimization[J].MathematicsofOperationsResearch,1996,21(3):513-528.

[13]SHAPIROA,DENTCHEVAD,RUSZCZYNSKIA.LecturesonStochasticProgramming:ModelingandTheory[M].Philadeiphia:SIAM,2009.

[14]XUH.Sampleaverageapproximationmethodsforaclassofstochasticvariationalinequalityproblems[J].AsiaPacificOperationalResearch,2011,27(1):103-119.

[15]ROBBINSH,MONROS.Astochasticapproximationmethod[J].AnnMathematicalStatistics,1951,22(3):400-407.

[16]ROBINSONSM,MONROS.Onastochasticapproximationmethod[J].AnnMathematicalStatistics,1954,25(3):463-483.

[17]JIANGHY,XUHF.Stochasticapproximationapproachestothestochasticvariationalinequalityproblem[J].IEEETransactionsonAutomaticControl,2008,53(6):1462-1475.

[18]KOSHALJ,NEDICA,SHANBHAGUV.Regularizediterativestochasticapproximationmethodsforstochasticvariationalinequalityproblems[J].IEEETransactionsonAutomaticControl,2013,58(3):594-609.

[19]NEMIROVSKIA,JUDITSKYA,LANG,etal.Robuststochasticapproximationapproachtostochasticprogramming[J].SIAMJOptim,2009,19(4):1574-1609.

[20]JUDITSKYA,NEMIROVSKIA,TAUVELC.Solvingvariationalinequalitieswithstochasticmirror-proxalgorithm[J].StochasticSystems,2011,1(1):17-58.

[21]BERTSEKASDP,TSITSIKLISJM.Neuro-dynamicprogramming[J].AthenaScientific,1996,27:1687-1692.

[22]ERMOLIEVY.StochasticQuasigradientMethods,NumericalTechniquesforStochasticOptimization[M].NewYork:Springer-Verlag,1988.

[23]KUSHNERHJ,YING.StochasticApproximationandRecursiveAlgorithmsandApplications[M].NewYork:Springer-Verlag,2003.

[24]ORMANA.Optimizationofstochasticmodels,theinterfacebetweensimulationandoptimization[J].OperationalResearchSociety,1998,49(6):675-675.

[25]FREYJ.Introductiontostochasticsearchandoptimization:estimation,simulation,andcontrol[J].Wiley-Interscience,2004,46(3):368-369.

[26]MALITSKYY.Projectedreflectedgradientmethodsformonotonevariationalinequalities[J].SIAMJOptim,2015,25(1):502-520.

[27]BAIOCCHIC,CAPELOA.VariationalandQuasivariationalInequalities[M].NewYork:JohnWiley,1984.

[28]ROBBINSH,SIEGMUNDD.Aconvergencetheoremfornonnegativealmostsupermartingalesandsomeapplications[C]//OptimizingMethodsinStatistics.RustagiJS,ed.NewYork:Academic,1971:233-257.

[29]PFLUGGC.Optimizationofstochasticmodels[C]//TheInterfaceBetweenSimulationandOptimization.NewYork:KluwerAcademic,1996.