SPH求解器的開發及其在液艙晃蕩數值模擬中的應用

尹梓煒 陳曉明 趙成璧

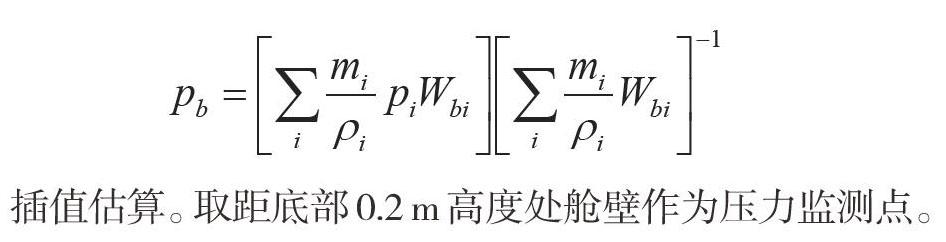
摘 要：本文提出一種改良的SPH固壁邊界條件處理方法，并基于此開發適用于模擬液艙晃蕩的數值求解器。采取該求解器對液艙晃蕩現象進行數值模擬，結果與相關文獻結果相當吻合，驗證了其可靠性和準確性。在此基礎上，通過計算分析橫蕩狀態下不同隔板高度液艙晃蕩時所產生的壁面壓力和液體重心高度變化趨勢，探討了隔板高度對液艙晃蕩的影響規律和物理機制，并為防蕩隔板的設計提出合理建議。

關鍵詞：SPH；固壁邊界條件；液艙晃蕩；數值模擬

中圖分類號：U661.74 文獻標識碼：A

Abstract： A modified treatment for rigid boundary condition of SPH method is proposed in this paper， and a numerical solver that suitable for sloshing simulation is developed based on this SPH method. The phenomenon of liquid sloshing in a tank is simulated by using this solver， and the numerical simulation results are in good agreement with the results from the related literature， which verifies the reliability and accuracy of the model. On the basis of that， through the calculation and analysis of the wall pressure and the trend of liquid gravity center height， which generated by sloshing with different baffle lengths under the sway condition， this paper preliminarily discusses the effect and physical mechanism of baffle length on sloshing and proposes reasonable suggestions about the design of anti-sloshing baffle.

Key words： SPH； Rigid boundary condition； Sloshing； Numerical simulation

1 引言

液艙晃蕩是指在部分充液的容器中，其內部液體在外部激勵下產生運動的現象。液艙晃蕩是船舶航行中遇到的常見現象，具有較強的隨機性和非線性。液體晃蕩產生的瞬時壓力可對艙壁結構造成損傷，同時晃蕩產生的附加力矩會影響船舶穩性，危害船舶安全，因此液艙防晃是船舶工程領域的基礎性課題，具有重要的工程應用價值。

液艙晃蕩問題的研究方法主要分為實驗、理論分析和數值仿真。隨著計算機科學的發展，數值分析已經成為研究液艙晃蕩問題的重要手段。傳統的數值方法如MAC、VOF等是基于網格對流場進行求解，在處理液艙晃蕩這類帶自由液面的強非線性運動問題時存在困難。光滑粒子流體動力學方法（SPH），最早由Lucy[1]和Monaghan[2]等分別獨立提出用于解決天體物理學問題，后經過改進引入到水動力學中。SPH作為一種無網格的拉格朗日方法，它克服了無網格方法在處理流體自由面大變形問題上的弱點，近年來逐漸被應用于液艙晃蕩問題的研究。

較早期的有Iglesias[3][4]等利用SPH方法先后研究了減搖水艙晃蕩特性和不同頻率下液艙晃蕩力矩幅值等問題，后來崔巖[5]等運用SPH方法模擬分析了二維矩形水槽在激勵頻率接近一階固有頻率的縱蕩過程中的晃蕩現象。在基于SPH方法的液艙晃蕩數值模擬中，邊界條件的處理十分關鍵，而上述文獻均采用Lennard-Jones斥力模型實施固壁邊界條件。該模型對靠近邊界的粒子施加強斥力，這容易導致粒子的初始分布被破壞，且時間步長受到嚴格的限制。同時為了防止粒子穿透邊界，特別是在邊界形狀突變處，往往使用多層邊界粒子，降低了計算效率，且會導致邊界附近產生明顯的壓力振蕩。為改善該問題，Shao[6]等提出耦合動力學邊界的SPH方法并研究了二維液艙晃蕩問題，得到較為精確的流場壓力。Chen[7]等在此基礎上修正其人工斥力的表達式，模擬了二維矩形容器在液艙晃蕩下的艙壁砰擊壓力并進行了實驗對比，獲得了讓人滿意的結果。

基于上述研究成果，為了獲得更為精確的液艙晃蕩模擬結果，本文在提出一種改良的固壁邊界條件處理方法基礎上，自主開發了適用于液艙晃蕩的SPH數值求解器，并進一步研究了隔板高度對晃蕩行為的影響，從而擴展了SPH方法在液艙晃蕩中的應用。

2 SPH求解器的開發

2.1 SPH基本方法和理論

SPH方法中[8]，計算域被離散為一系列具有相互作用的粒子，某時刻粒子的物理量可由一定光滑半徑內的周圍粒子通過核函數（如三次樣條函數等）估計得到。基于SPH的核近似和粒子近似思想，考慮重力下控制流體運動的Navier-Stokes方程可離散為如下形式：

壓力通過下列狀態方程求得：

2.2 自適應邊界粒子法向斥力模型

Akinic[10]提出了一種流固耦合邊界方法，該方法引入邊界粒子質量函數，考慮邊界粒子的影響對流體粒子的密度和受力進行修正。本文基于該方法的思想并對其進行改進，只考慮法向斥力，提出一種改良的自適應邊界粒子法向斥力模型，得到考慮邊界粒子b的貢獻的SPH控制方程如下：

由上式可知，由于核函數隨距離增加而單調遞減的性質，邊界粒子分布密集的地方不會產生過大斥力，分布稀疏的地方也不會產生過小的斥力，因此相對于傳統SPH邊界處理方法具有自適應性。且該方法斥力大小又與流體粒子自身壓力大小有關，只在法向施加排斥力，減少邊界粒子對流場的擾動，可以使粒子在邊界處受力更均勻。

以簡單的潰壩模型為算例。從圖1的速度矢量對比可以看出：傳統的Lennard-Jones斥力模型中潰壩水頭前沿的粒子運動十分不均勻，明顯是由于產生的瞬時斥力過大導致；而本文方法中的底部邊界粒子產生足夠而均勻的斥力，有效避免粒子在固壁邊界發生非物理穿透的現象，同時使粒子運動平滑有序，證明本文方法的效果明顯優于傳統的斥力模型。

2.3 算法流程

SPH求解器的算法流程如圖2。

其中：鄰域粒子搜索方法有全配對搜索法、鏈表搜索法和樹形搜索法等方法；時間積分的方法可采用蛙跳法、預測校正法和龍格庫塔法等方法。本文采用鏈表搜索法進行鄰域搜索，采用蛙跳法進行時間積分，時間步長滿足CFL條件，具體見參考文獻[8]。

3 基于SPH求解器的液艙晃蕩數值模擬

3.1 典型液艙晃蕩實驗

Chen[7]的實驗是研究液艙晃蕩的典型實驗，并給出了較準確的SPH模擬結果。為了驗證本文液艙晃蕩SPH方法數值求解器的可靠性和精確性，本文模擬了Chen液艙晃蕩算例，并與其實驗結果和模擬結果進行比較。

計算模型中矩形液艙長和高為L=H=1 m、充液深度D=0.3 m、橫搖頻率3.81rad/s、振幅5°，容器底部中心處為軸心。計算采用流體粒子數12 870、時間步長1×10-4 s進行模擬，流體壓縮率控制在0.1%附近。

圖3和圖4分別為矩形液艙在激勵頻率3.81 rad/s的橫搖下晃蕩的四個典型時刻的chen實驗結果和本文模擬結果。從圖中可以看出，本文的SPH模型有效地模擬了自由液面形態，同時獲得了較精確的均勻壓力分布。

在本文中，基于SPH的核近似和粒子近似的思想，邊界粒子b的壓強通過周圍流體粒子根據

插值估算。取距底部0.2 m高度處艙壁作為壓力監測點。

圖5所示為壓力監測點在計算時段2～10 s的壓力時間歷程。由圖5可知，本文SPH方法的壓力計算結果與Chen的數值模擬結果的變化趨勢基本一致，同時壓力的峰值則與Chen的實驗結果更為接近，證明本文SPH方法在液艙晃蕩的數值模擬應用具有更高的可靠性和精確性。

3.2 防蕩隔板高度對液艙晃蕩影響

為進一步研究不同液艙結構對晃蕩行為的影響，本文在與3.1算例尺寸相同的矩形液艙中添加防蕩隔板，模擬了不同高度的I型單隔板在橫蕩頻率接近液艙一階模態的橫蕩工況下的防蕩效果對比。

根據線性理論，由 可得矩形液艙晃蕩的一階固有頻率為ω1=4.76 rad/s，對液艙施加簡諧激勵x=Asin（ωt），取ω=1.166ω1、振幅A=0.05 m。在橫蕩工況下，為達到防蕩效果最大化，在液艙中央豎向布置I型隔板，隔板高度l分別取0.25 D、0.5 D和0.75 D。同時為了分析方便，取距離艙壁底部0.3 m處側壁作為壓力監測點。

圖6（1）描述了不同單隔板尺寸工況下艙壁壓力計算監測點在計算時段2～10 s的壓力時間歷程。圖6（2）描述了不同單隔板尺寸工況下在計算時段0～10 s液體重心高度的時間歷程。由圖6（1）可知，隨著隔板高度的增加，整體上壓力峰值呈減少趨勢且雙峰特性減弱，當隔板高度為0.75 D時最大壓力峰值能降至無隔板狀態下的24.5%。同時，當隔板增加到一定高度后，壓力峰值對隔板高度變化的敏感度降低。由圖6（2）可知，隔板高度和液體重心高度呈明顯的正相關，其中當隔板高度為0.75D時，重心高度波動最大幅值可降至無隔板狀態時的19.2%。

為了進一步研究液艙晃蕩時隔板高度對壓力峰值影響的物理機理，我們對不同隔板高度下的液艙流場速度進行對比分析。

圖7反映了t=2.26 s時刻不同隔板高度的流場速度矢量和艙壁壓力。可以看出：隨著隔板高度的增加，隔板附近流場受到干擾，出現了紊亂并逐漸產生了渦。此時，渦街阻尼效應對較大波高的形成產生了削弱作用，有效抑制了液艙晃蕩時的液面劇烈波動，從而有效地降低艙壁晃蕩時的艙壁壓力。

不過，結合圖6（1）可知，當隔板到達一定高度后，其對艙壁壓力峰值的影響效果將減弱；同時圖7表明，隨著隔板高度的增加，隔板的渦街振動響應不斷增強，隔板的液體沖擊荷載作用不斷增大，這會導致隔板端部應力集中，因此從安全性和經濟型考慮，隔板高度應適中，建議隔板在具體設計時可采用本文數值模擬方法確定隔板高度尺寸。

4 結論

本文利用自主開發改進的SPH求解器研究了二維矩形液艙晃蕩問題，取得較好的應用效果。由數值模擬結果可以看出：

（1）本文改良的固壁邊界條件處理方法，能有效阻止粒子穿透邊界并使粒子在邊界處的運動均勻有序。以此為基礎自主開發的SPH求解器具有較高的可靠性和精確性，能很好地捕捉液艙晃蕩時的自由液面狀態，獲得較為準確的流場壓力值，是對液艙晃蕩現象有效的數值模擬手段，具有較好的應用前景；

（2）本文進一步的研究結果表明，防蕩隔板能明顯降低液艙晃蕩的幅度和艙壁壓力峰值，但從安全性和經濟性的角度出發，隔板高度應適中，不宜過高。

此外，SPH方法中在增加算法穩定性、提高計算精度和效率等方面尚有許多需要完善之處，本文的研究為進一步開發高效通用的SPH求解器以及拓展其應用領域打下了基礎。

參考文獻

[1]Lucy L B. A numerical approach to the testing of the fission hypothesis[J]. Astronomical Journal， 1977， （82）.

[2]Gingold R A， Monaghan J J. Smoothed particle hydrodynamics： theory and application to non-spherical stars[J]. Monthly Notices of the Royal Astronomical Society， 1977， 181（3）.

[3]Souto Iglesias A， Pérez Rojas L， Zamora Rodríguez R. Simulation of anti-roll tanks and sloshing type problems with smoothed particle hydrodynamics[J]. Ocean Engineering， 2004， 31（8）.

[4]Souto-Iglesias A， Delorme L， Pérez-Rojas L， et al. Liquid moment amplitude assessment in sloshing type problems with smooth particle hydrodynamics[J]. Ocean Engineering， 2006， 33（11）.

[5]崔巖， 吳衛， 劉樺. SPH方法模擬二維矩形水槽晃蕩過程[C]// 全國水動力學研討會. 2006.

[6]Shao J R， Li H Q， Liu G R， et al. An improved SPH method for modeling liquid sloshing dynamics[J]. Computers & Structures， 2012， s 100–101（6）.

[7]Chen Z， Zong Z， Li H T， et al. An investigation into the pressure on solid walls in 2D sloshing using SPH method[J]. Ocean Engineering， 2013， 59（2）.

[8]G.R.Liu， M.B.Liu， Liu，等. 光滑粒子流體動力學：一種無網格粒子法[M]. 湖南大學出版社， 2005.

[9]Monaghan J J， Gingold R A. Shock simulation by the particle method SPH[J]. Journal of Computational Physics， 1983， 52（2）.

[10]Akinci N， Ihmsen M， Akinci G， et al. Versatile rigid-fluid coupling for incompressible SPH[J]. Acm Transactions on Graphics， 2012， 31（4）.