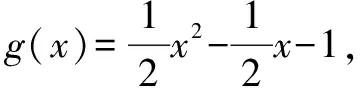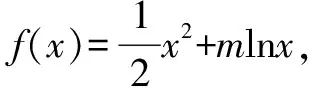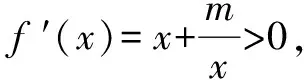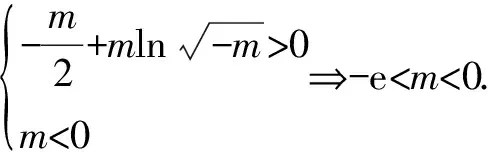二元函數不等式的證明方法
朱東海
(云南省蒙自市蒙自一中 661199)
在本刊2016年第34期中,我們談了一元函數不等式的證明方法,本文中我們來看如何證明二元函數不等式.
對于二元函數不等式的證明,首先考慮能不能轉化為一元不等式來證明.
一、變型后轉化為一元不等式的證明問題
1.利用函數的單調性變成同一函數的兩個函數(值)間的大小比較
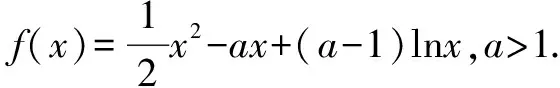
(1)討論函數f(x)的單調性;
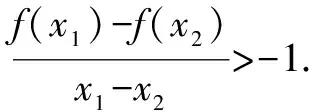
解(1)依題意f(x)的定義域為(0,+∞),
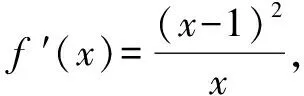
②若a-1<1,而a>1,故1 則當x∈(a-1,1)時,f′(x)<0; 當x∈(0,a-1)或x∈(1,+∞)時,f′(x)>0. 故f(x)在(a-1,1)單調減少,在(0,a-1),(1,+∞)單調增加. ③若a-1>1,即a>2,同理可得f(x)在(1,a-1)單調減少,在(0,1),(a-1,+∞)單調增加. (2)由于當x1>x2>0時, 只需證明f(x)+x在(0,+∞)上是增函數.令函數 對于冪、指數形式的不等式,可以先取對數,再化為對數不等式來證明 例2 (山東省桓臺第二中學2015屆高三數學理21)設函數f(x)=x-a(x+1)ln(x+1) (a≥0). (1)如果a=1,求函數f(x)的單調遞減區間; (2)若函數f(x)在區間(-1,e-1)上單調遞增,求實數a的取值范圍; (3)證明:當m>n>0時,(1+m)n<(1+n)m. 解(1)依題意f(x)的定義域為(-1,+∞),f′(x)=1-aln(x+1)-a. 當a=1時,f′(x)=-ln(x+1),令f′(x)<0得x>0,所以函數f(x)的單調遞減區間是(0,+∞). 由(1)知,當a=1時,函數f(x)=x-(1+x)ln(1+x)在區間(0,+∞)單調遞減,所以當x>0時,f(x) 例1 (廣州市2015屆高三)已知函數f(x)=ax2-blnx在點(1,f(1))處的切線為y=1. (1)求實數a,b的值; (2)是否存在實數m,當x∈(0,1]時,函數g(x)=f(x)-x2+m(x-1)的最小值為0,若存在,求出m的取值范圍;若不存在,說明理由; 解(1)f(x)=ax2-blnx,其定義域為(0,+∞), 解得a=1,b=2. (2)g(x)=f(x)-x2+m(x-1)=m(x-1)-2lnx,x∈(0,1], ①當m≤0時,g′(x)<0,則g(x)在(0,1]上單調遞減, ∴g(x)min=g(1)=0. ∴g(x)min≠0. 綜上所述,存在m滿足題意,其取值范圍為(-∞,2]. (3)證明: 令g(x)=x-1-2lnx,由(2)知,當m=1時,g(x)=x-1-2lnx在(0,1)上單調遞減, ∴x∈(0,1)時,g(x)>g(1)=0, 即x-1>2lnx. 例1 (太原五中2014—2015學年度第二學期階段檢測高三數學(理))已知函數f(x)=lnx. (2)若直線y=ax+b是曲線y=f(x)的切線,求ab的最大值; (3)設A(x1,y1),B(x2,y2),C(x3,y3)是曲線y=f(x)上相異三點,其中0 在某一個區間上證明不等式,若不等式涉及的兩變量就是區間的兩個端點,則把其中的一個端點視為自變量來構造函數. 例1 (2009年重慶沙坪壩區校級模擬)已知f(x)=ex-ln(x+1)-1(x≥0), (1)求函數f(x)的最小值; (2)如果求0≤y≤x,求證: ex-y-1>ln(x+1)-ln(y+1). 若不等式涉及的兩個變量不是區間的兩個端點,同樣可以把其中一個視為自變量來構造函數. (1)求實數a,b的值; (2)若φ(x)=f(x)-g(x),求證:當x∈(-1,+∞)時,φ(x)≤0恒成立; (2)當a=0,b=1時,φ(x)=f(x)-g(x)=ln(x+1)-x, φ(x)max=φ(0)=0,從而φ(x)≤0成立,故當x∈(-1,+∞)時,φ(x)≤0恒成立. 例1 (貴州省八校聯盟2015屆高三第二次聯考數學理21)已知函數f(x)=lnx. (1)求函數g(x)=f(x+1)-x的最大值; 1.|f(x1)-f(x2)|≤M?[f(x)]max-[f(x)]min≤M (1)若存在x>0,使f(x)≤0成立,求實數m的取值范圍; (2)設1 x(0,-m)-m(-m,+∞)f ′(x)-0+f(x)↘極小值↗ 所以對?x>0,f(x)>0恒成立,則實數m的取值范圍是(-e,0]. 故?x>0,使f(x)≤0成立,實數m的取值范圍是(-∞,-e]∪(0,+∞). 參考文獻: [1]朱東海. f(x)≥ag(x)恒成立的一個充要條件[J].語數外學習,2012(06). [2]朱東海.利用導數證明不等式時怎樣構造函數[J].語數外學習,2013(11).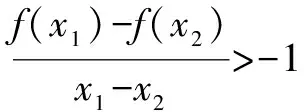

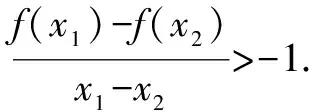





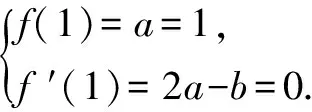
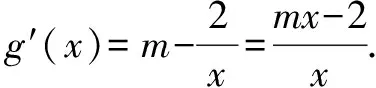

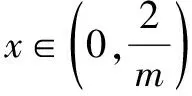
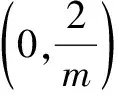


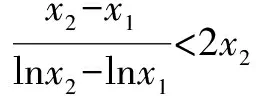
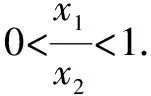

二、借助第三量
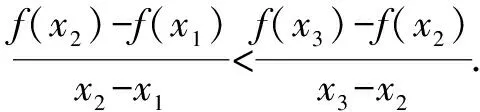
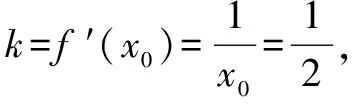
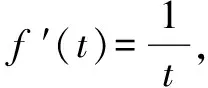





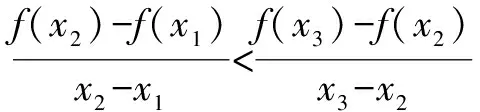
三、用端點變量法構造函數



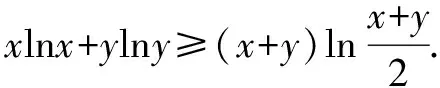
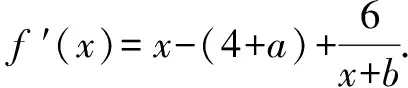

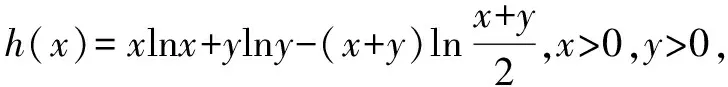
四、轉化為代數不等式來證明
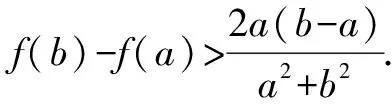
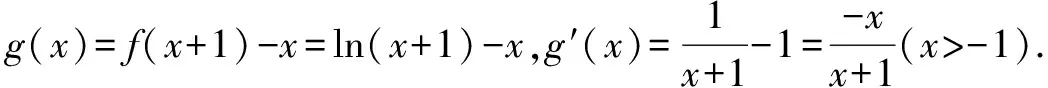


五、轉化為最值之間的關系