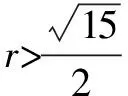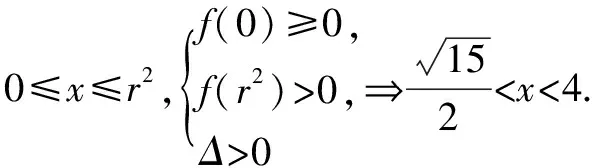關于圓錐曲線中的聯列問題
周瀟滔
(浙江省嵊州中學高二(16)班 312400)
一、問題引入
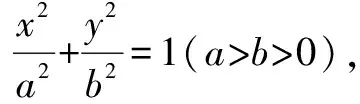
這看似是一道基礎題,由于圓和橢圓關于x軸對稱,并且總有橢圓的頂點這一個交點,所以圓方程和橢圓方程聯列一下根據判別式,就可以出結果了,但事實正是如此嗎?我們來實踐一下.
解b2x2+a2y2=a2b2①,
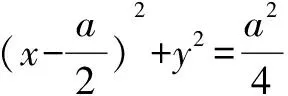
將③代入①整理得:
(b2-a2)x2+a3x-a2b2=0.
Δ=a6+4a2b2(b2-a2)>0?(a2-2b2)2>0
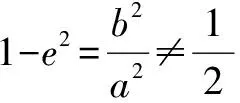
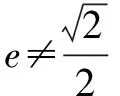
3x2+4y2=12①,
(x-1)2+y2=1②.
將②代入①得:
8x-x2=12?x1=2,x2=6.
那么問題出在了哪里?
首先我們無法保證該圓與橢圓的值域相同,換句話說,當該圓與橢圓值域相同是顯然必有三個交點,故我們只需討論值域不同時的情況.
既然值域不同,這必定不是等價代換.
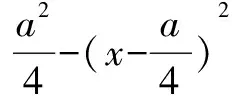
先前我們已證明方程(b2-a2)x2+a3x-a2b2=0必有根,且一根為x2=a,
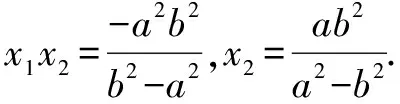

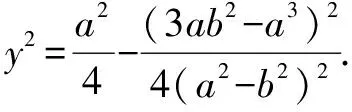
若y2<0即a2(a2-b2)2<(3ab2-a3)2
小結:所以聯列方程,用方程判別式來解答并不能保證排除原方程增根的出現.也就不能用判別式來判斷實根的情況了.但是若對聯列后的方程進行定義域的約束,即在0 在進行二次曲線聯列時我們要牢記約束條件,那么,當我們將直線與二次曲線聯列時,為什么可以“忽略”約束,直接用判別式呢? 整理得(a2k2+b2)x2+2mka2x+m2a2-a2b2=0. Δ=4m2k2a4-4(a2k2+b2)(m2a2-a2b2)>0?b2+a2k2>m2. 那么滿足這個條件的兩根就一定落在定義域內嗎? 我們不妨算出這兩根. 如果要證明其符合定義域,只要證明-a≤x1 假設x2≤a成立, a2k2+b2>0,a2k2+2akm+m2=(ak+m)2≥0, 故假設成立,同理x1≥-a也成立 的確我們證實了x1,x2都會落在橢圓內部,也就是說只要滿足判別式大于等于0,就會有實數根. 那么我們再從等價代換角度來看這個問題. ①中的y2必須滿足0≤y2≤b2,而y2=(kx+m)2②中的y2卻只滿足了y2≥0, 所以這并非等價代換,即必須對x進行約束0≤(kx+m)2≤b2. 總結:直線與二次曲線聯列并非不需要約束條件,只是在運算過程中約束會自動成立. 所以無論二次曲線和二次曲線還是直線和二次曲線聯列都需要進行有效的等價代換只是一個有必要寫出約束條件,另一個約束已成立了. 1.探索二次曲線聯列“無需”約束情況 我們來簡單地看一道題 例1 求t的取值范圍使得拋物線y2=2px與拋物線x2=2p(y+t)有交點(p>0). 把③代入②得 用判別式顯然不行,倒不如用導數來做方便. 記f(y)=y4-8p3y-8p3t, f(y)′=4y3-8p3. ∴24/3p4-8p421/3-8p3t≤0, 顯然兩條曲線相切時,y2=2px在x軸上方的曲線表示為 因為兩條曲線在(x0,y0)處的切線為同一條,故其斜率相同, 可以發現相切時的t與之前算出來的最小值正好相等而且不難看出當t越來越大時曲線x2=2p(y+t)不斷下移,那么必與曲線y2=2px有交點,故答案正確. 我們再回到最初代換. y2=2px中的x∈[0,+∞),x2=2p(y+t)中的x∈R. 雖然兩個x值域并不相同,但y2=2px中x的取值范圍是x2=2p(y+t)中x的子集. 這樣的代換使被代者和代者之間為子集關系,縮小范圍的代換依然成立. 2.探究直線與二次曲線聯列“需要”約束的情況 直線與二次曲線聯列一般無需考慮約束,但也有例外. 我們來看一下 按照常規思維,我們聯列利用判別式可得出結果. 但這真的是最終答案嗎? 有時簡單的題目不能想當然去做,理所當然的聯列使用判別式,有時也有陷阱,或許畫個圖進行觀察可以發現一些問題. 故無論二次曲線與二次曲線,還是直線與二次曲線都需要謹慎下筆,沒有什么絕對的成立與不成立,多想一下,繞過題設的陷阱,用實踐去檢驗. 高考中兩個二次曲線聯列的問題也屢見不鮮,單近年來似乎為了回避這個暗區,這樣的題目漸漸少了,下面我們來看一道2009年的全國卷高考題 如圖,已知拋物線E:y2=x與圓M:(x-4)2+y2=r2(r>0)相交于A,B,C,D四個點. (1)求r的取值范圍; (2)當四邊形ABCD的面積最大時,求對角線AC,BD的交點p的坐標. 當年許多考生一拿到這道題便將y2=x直接與圓(x-4)2+y2=r2,聯列運用判別式來求解: y2=x①, (x-4)2+y2=r2②. 將①代入②得 看似正確的解法卻又不幸掉入了出題者的陷進之中很明顯考生沒有抓住“等價”二字,盲目地替代導致擴大了范圍.現在對原方法改進一下: 代換得:x2-7x+16-r2=0(4-r≤x≤4+r). 也就是說在x∈[4-r,4+r]范圍內,必須保證x2-7x+16-r2=0有兩個正解. 設f(x)=x2-7x+16-r2,則 盲目代換只會增加出現增根的可能性,遇見二次曲線的聯列切忌直接使用判別式. 評析仔細觀察本題在對x約束時我們還可以做文章. 上文中的4-r≤x≤r+4是對(x-4)2+y2=r2中的x進行約束,約束使得解出來的x滿足在圓內,那么我們難道不能對(x-4)2+y2=r2中的y2進行約束嗎? 第一種方法固然成立,而第二種方法本質是約束y2.因為y2=x, 那么方程如果有解,且這個解是符合y2∈[0,r2],那么對于(x-4)2+y2=r2來說這個解就不會是增根,因此這個約束是成立的. 參考文獻: [1]徐燕.高中生對圓錐曲線的理解[D].上海:華東師范大學,2009.二、溫故知新
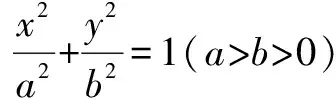
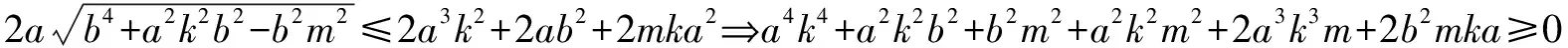
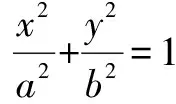
三、深入研究
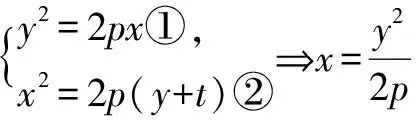
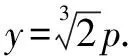
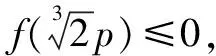
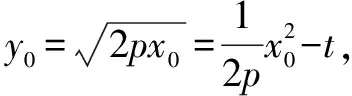
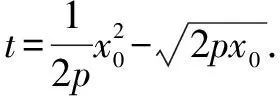
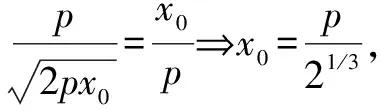
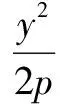
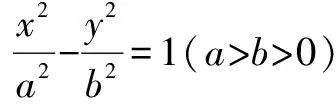
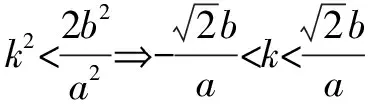
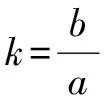
四、走進高考