基于概率假設密度濾波的多目標跟蹤算法*

王春平，劉江義，楊文兵

（1.陸軍工程大學石家莊校區，石家莊 050003；2.陸軍重慶軍代局駐9804廠軍代室，云南 曲靖 655000）

0 引言

多目標跟蹤在軍事領域和民用領域有著廣泛的應用，傳統的多目標跟蹤是采用“量測-航跡”這種基于航跡關聯的方法，這類跟蹤方法的關鍵問題是如何進行有效的數據關聯，典型的數據關聯方法包括最近鄰法、聯合概率數據關聯算法（JPDA）和多假設方法（MHT）等［1-2］。這些數據關聯方法在目標個數增加的情況下，計算復雜性呈指數增加，在目標機動性強或者目標密集的情況下可能出現關聯錯誤導致跟蹤失敗的問題［3］。

為了解決數據關聯計算量大和避免航跡關聯錯誤，最近幾年提出了利用隨機有限集（RFS）理論來進行多目標跟蹤的方法。Mahler于2003年進一步提出了使用多目標后驗概率分布的一階統計量來近似代替多目標的后驗概率分布，以此遞推近似計算目標數和目標狀態，并提出了概率假設密度濾波（Probability Hypothesis Density Filter）［4］。

PHD以最小損失將多目標狀態集合的后驗PDF投影在單目標狀態空間上，則PHD濾波器只需在單目標狀態空間進行遞推，避免了多目標貝葉斯濾波器在隨機有限集（RFS）空間上進行遞推，其計算復雜度大大降低。PHD的物理意義是狀態空間中目標個數的后驗強度，而對應PHD峰值為目標狀態［5］。

1 PHD濾波算法及研究進展

1.1 PHD濾波原理

假設存在任一RFSΞ，它可以通過一個隨機計數測度來定義［6］：

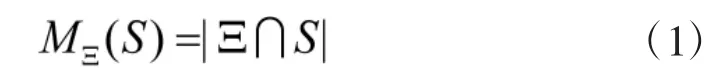
其中，表示中元素的個數，假定在多目標跟蹤系統中有n個目標，假設k時刻目標為狀態xk，隨機集Ξ可以用的廣義密度來表示：

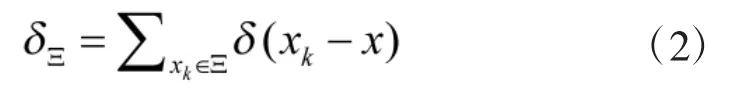
式中，代表中心位于x的Dirac delta函數。

假設存在RFSΞ，其在物理上可等價地表示為廣義密度函數。因而隨機集可以表示為隨機密度密度定義隨機集Ξ的概率假設密度（PHD）函數為：。令表示RFS的Ξ的概率分布，利用隨機

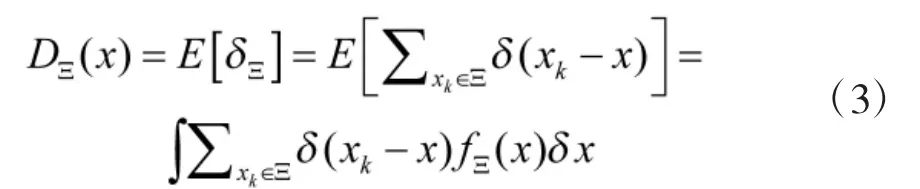
多目標跟蹤過程中，會出現目標的新生、衍生以及消失的現象，目標的狀態和個數是變化的，另外，由于傳感器檢測性能和背景干擾的影響，會存在干擾和虛警信息。根據多目標的貝葉斯理論以及有限集統計學理論（FISST），得到PHD濾波的預測和更新公式：

預測：

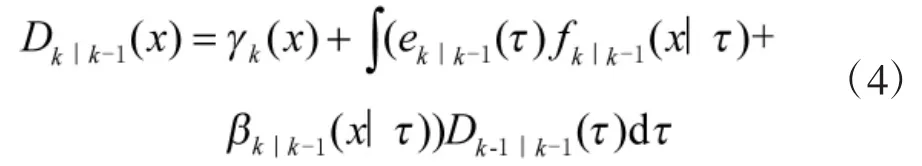
更新：

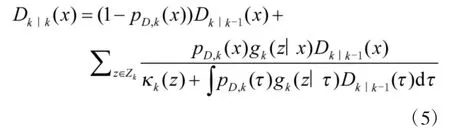
其中，表示k時刻新生目標的強度，表示k-1時刻狀態為的目標在k時刻的存活概率，表示目標的狀態轉移概率密度函數，表示為單傳感器單目標似然函數，時刻的目標在k時刻的衍生出的目標強度，表示k-1表示目標的檢測概率，Zk為k時刻目標的觀測集，為雜波PHD函數。

1.2 PHD濾波算法研究進展

PHD濾波算法避免了多目標跟蹤過程中的數據關聯，尤其適用于目標個數未知，信噪比較低的多目標跟蹤。針對PHD濾波對目標個數估計存在偏差的問題，PHD濾波的提出者Mahler對PHD進行改進，放松了對目標數目的泊松假設，將目標狀態的二階信息加入PHD濾波中［7-8］，對目標的PHD和目標個數同時進行更新，提出了勢概率假設密度（CPHD）濾波；為了提高跟蹤性能，學者提出了很多擴展的CPHD濾波算法，文獻［9］提出了改進CPHD濾波器，利用更新過程中的量測似然比來提高目標數目的估計，通過把模糊目標當作待檢測目標來修正勢分布；文獻［10］提出的改機CPHD濾波算法將上一時刻在當前時刻的存活目標和當前時刻的新生目標區分開，利用每幀的觀測來調節目標新生強度。另外，學者針對目標運動模型、多檢測情況、雜波分布規律假定等內容進行研究和改進。

1）目標運動模型。隱馬爾科夫鏈（HMC）模型是單目標和多目標跟蹤的理論基礎，但由于該模型強烈的獨立性，它在實際應用中經常是無效的。2000年，Pieczynski［11-12］提出了成對馬爾科夫鏈（PMC）模型作為放松這種假設的一種方法；Petetin和Desbouvries［13］于2013年提出了基于PMC運動模型的PHD（PMC-PHD）濾波器，他們證明，在放松的假設條件下，PMC-PHD濾波器比經典PHD濾波器有更好的跟蹤性能；文獻［14］給出了Petetin-Desbouvries濾波器的可靠的理論基礎，然而，理論分析表明：Petetin-Desbouvries濾波器是隱含的基于多目標HMC（M-HMC）模型，并不是真正的多目標PMC（M-PMC）模型，因此，該濾波器僅針對單獨的目標放松了HMC獨立假設，而不是針對整體的多目標系統；Mahler等［15］于2015年進行了多目標成對馬爾科夫鏈（M-PMCs）的第一次系統研究，并介紹了其在多目標檢測和跟蹤中的應用，介紹了兩種推導M-PMC轉移密度具體公式的方法。

2）多檢測情況。標準PHD濾波器假設一個目標在一個場景中最多有一個檢測量，但是，在很多實際場景中，一個目標可能通過多種傳輸路徑（也就是不同的觀測模型）產生多個檢測量。在文獻［16］中，目標產生的量測被建模為一個二值RFS和一個泊松RFS的混合模型，兩個RFS分別代表一個直接路徑的檢測量和其他多個路徑檢測量，但該方法不能處理常見的沒有首選（直接的）路徑的情況；文獻［17］利用隨機集統計（FISST）理論推導出了一個新的適合多檢測的PHD觀測更新公式，在這個多檢測PHD（MD-PHD）濾波器的推導過程中沒有在標準PHD公式所作近似的基礎上進行更多的近似。

3）雜波分布規律假定。大部分多目標檢測和跟蹤算法都是假定背景雜波過程的統計規律已知，PHD濾波器允許目標個數是隨機的，CPHD濾波器允許目標個數和雜波觀測的個數分布是隨機的。然而，在實際應用中，當實際的雜波統計規律相對于前一時刻統計規律差別較大時，跟蹤器的性能會劇烈降低，跟蹤器需要擺脫雜波過程的先驗模型來進行檢測和跟蹤多個目標。Mahler［18］于2009年提出了一種滿足上述要求的CPHD濾波器，該濾波器通過泊松雜波產生器產生雜波觀測集合，所有的雜波過程是未知個數的雜波產生器的組合，因此，提出的CPHD濾波器有組合的計算復雜度；Chen等［19-20］提出了基于伯努利雜波產生器的PHD濾波器，伯努利雜波產生器就像一個具有檢測概率和帶參似然函數的“雜波目標”，Mahler［21］隨后將這種方法擴展到 CPHD 濾波器；Mahler［21-22］于 2010 年提出了基于伯努利雜波產生器的κ-CPHD濾波器，隨后Mahler［23］利用 beta-Gaussian mixtures（BGMs）技術在精確的閉環形式下實現了κ-CPHD濾波器的簡單版本并證明其具有良好的性能；Mahler和Vo等［24］于2014年對κ-CPHD濾波器進行改進，推導出雜波觀測個數分布和目標勢分布的公式，他們實現并證明了濾波器的有效性；Mahler［25］于2014年對κ-CPHD濾波器進行擴展，使其也能夠估計目標新生過程；Vo，Hoseinnezhad，和 Mahler［26］在2011年將伯努利產生器方法擴展為多伯努利濾波器；Mahler等［27］利用二階二次雜波產生器代替伯努利雜波產生器推導出了CPHD濾波器,該濾波器可以利用 BGMs和 Dirichlet-Gaussian mixture（DGM）技術在精確的閉環形式下實現。

2 PHD濾波實現方法及進展

2.1 PHD濾波實現方法

由PHD在貝葉斯理論下的遞推公式可以看出，求解PHD濾波的更新過程中存在積分運算，一般沒有解析解，目前PHD濾波的實現方法主要有兩種，一種是基于序貫蒙特卡羅（SMC，也就是粒子濾波）實現［28］，一種是基于高斯混合（GM） 實現［29］。SMC-PHD濾波和GM-PHD濾波提出以后，針對這兩種實現方法存在的問題，國內外學者進行了很多研究和改進。

2.2 PHD濾波實現方法進展

1）SMC-PHD濾波器進展。概率假設密度（PHD）的SMC實現方法由于需要大量粒子來近似導致計算效率較低，特別是在目標數目較大和雜波密集的情況下，為提高運算速度，文獻［30］提出了基于多處理器的并行SMC-PHD濾波算法框架，處理相同的算法時，并行實現方法相比于順序實現方法有相當大的增速；Ju Hong Yoon［31］針對粒子退化問題提出了一種利用無跡信息濾波和門限技術的新的IS函數；為了提高雜波環境下輔助SMC-PHD濾波的精度性能，Ju Hong Yoon［32］提出了無跡序貫蒙特卡羅概率假設密度（USMC-PHD）濾波；文獻［33］提出了一種PHD濾波器改進的SMC實現方法—Sigma門限SMC-PHD濾波器，提高總體的處理速度，更重要的是，避免門限外雜波的干擾，獲得更好的魯棒性和更準確的估計。

2）GM-PHD濾波器進展。當目標相互靠近時，GM-PHD濾波器經常不能正確地估計目標的數目和狀態，為解決上述問題，文獻［34］提出了一種目標權重重分布方案，可以適當地改進距離緊密的目標的權重；理論上，GM-PHD濾波器在濾波迭代過程中影響漏檢的因素不能適當地合并時，連續漏檢情況下的濾波器性能會降低，文獻［35］提出了一種精制GM-PHD（RGM-PHD）跟蹤器，提出了一個狀態精制步驟和一個狀態提取步驟以提高濾波器的跟蹤性能。對于機動目標跟蹤，已有的基于聯合分布的多模型高斯混和概率假設密度（MM-GM-PHD）濾波器相對比較復雜，文獻［36］利用了模型條件分布和模型概率兩個概念，描述每個高斯分量都利用多模型方法來進行估計，最終結果是多模型估計的融合。

3）Clark D等［37］權衡SMC-PHD 以及 GM-PHD的優劣，提出了PHD濾波器的高斯粒子執行方法（Gaussian particle implementations of PHD，GMP-PHD），GMP-PHD濾波在預測和更新過程中需要進行粒子的近似和重新采樣，這在一定程度上影響了跟蹤的精度和實時性，文獻［38］針對這個問題，通過粒子的方式表示并傳遞目標PHD的預測值，直接利用這些表征PHD預測值的粒子進行更新，最后利用具有最大似然性的粒子將更新后的PHD表示為混合高斯形式，改進算法的跟蹤精度和實時性得到很大提高。

3 PHD應用領域及進展

PHD濾波因為特有的優勢成為了這幾年的研究熱點，越來越多的學者將PHD應用于弱小多目標TBD跟蹤、多擴展目標跟蹤和多傳感器多目標跟蹤等領域。

3.1 基于PHD的弱小多目標TBD跟蹤

在傳統目標跟蹤中，利用檢測門限獲得目標觀測，這種處理方法一般被稱為跟蹤前檢測（DBT）。DBT方法的潛在缺陷在于，表示目標的有用信息由于門限處理過程有可能被丟棄，這樣會導致不完全觀測或者目標丟失，特別是在SNR較小的情況下，跟蹤性能更差［39］。

利用無門限的數據同時檢測和跟蹤一般稱為檢測前跟蹤（TBD），在PHD濾波框架下，文獻［40］提出了一種多目標TBD方法；文獻［41］將PHD濾波器擴展到多輸入多輸出雷達的多目標TBD應用；文獻［42］提出了一種基于SMC-PHD的多目標TBD方法，以適應更普遍的點擴散目標的觀測模型；文獻［43］通過改進文獻［42］提出的原有算法，提出了適用于非標準點觀測模型的基于SMC-PHD的多目標TBD算法。

3.2 基于PHD的多擴展目標跟蹤

經典的目標跟蹤假定每個目標一個時刻最多產生一個觀測，這個假設在目標與傳感器的距離相對于目標大小大很多時是正確的。然而，在實際的目標跟蹤中，當目標在一個高精度雷達附近區域時，雷達在一個時刻可以從一個目標的不同邊緣反射點獲得不止一個觀測，這類目標被稱為擴展目標［44-45］。

已存在的擴展目標濾波器包括ET概率假設密度 （ET-PHD） 濾波器、ET高斯混合PHD（ET-GM-PHD）濾波器、ET-GM-CPHD濾波器、ET高斯逆 Wishart PHD（ET-GIW-PHD）濾波器、ET 伽馬 GIW-PHD（ET-GGIW-PHD） 濾波器和ET-GGIW-CPHD濾波器［46-47］。理論上，以上濾波器需要當前觀測集所有可能的分區用于濾波更新。

ET-GM-PHD濾波器和ET-GM-CPHD濾波器采用了距離分區和帶子分區的距離分區［44,48］，然而，以上分區算法需要更高的計算復雜度來獲得準確的分區，為了在不損失跟蹤性能的條件下減小計算壓力，文獻［49］提出了一種基于模糊自適應諧振理論（ART）［50］的快速分區算法；在 ET-GIW-PHD濾波器和ET-GGIW-PHD濾波器中，為了處理一些尺寸不同并且空間相鄰的多擴展目標的情況，Granstr?m［51］等提出了兩個額外的分區方法：基于預測GIW-PHD成分的預測分區和基于期望最大化（EM）的期望最大化分區。

3.3 基于PHD的多傳感器多目標跟蹤

前面提到的多目標跟蹤算法大都應用于單傳感器的情況，為處理多傳感器多目標跟蹤，文獻［4］提出了迭代PHD濾波器，該濾波器性能受傳感器更新的順序和低檢測概率的影響。相比于迭代PHD濾波器，Mahler在文獻［52］中提出的乘積多傳感器PHD（PM-PHD）濾波器在勢估計和穩定性方面都有更好的性能。文獻［53］提出了真正雙傳感器PHD濾波器，該算法將從每個傳感器采集到的觀測集看作一個單元，并且把聯合觀測集分割為不同區域。文獻［54］研究了多傳感器標記誤差問題，文獻［55-56］給出了算法的高斯混合（GM）實現和序貫蒙特卡羅（SMC）實現。文獻［57］介紹了一種基于傳感器視場配置的聯合分割方法，這種方法可以大幅度降低更新步驟的計算壓力。

為減小傳感器更新的順序和低檢測概率的影響，文獻［58］提出了一種啟發式方法——改進的基于高斯混合實現的迭代矯正PHD；標記誤差補償已經成為多傳感器數據融合系統中的重要課題，文獻［59］提出了一種面向帶有標記誤差的多傳感器多目標跟蹤的高斯混合PHD濾波，通過將平移測量偏差的動力學引入到關聯密度函數來實現PHD遞推；文獻［60］提出了一種面向多普勒雷達多目標跟蹤的帶標記誤差增廣狀態的GM-PHD濾波，建立了增廣狀態的線性高斯運動模型和觀測模型。

4 結論

縱觀上述研究進展，著眼提高目標跟蹤精度和實時性的發展要求，基于PHD濾波的多目標跟蹤技術未來值得關注的方向可概括為以下4點。

4.1 PHD濾波實現方法研究

盡管廣大科研工作者對PHD濾波的兩種執行方法——SMC實現和GM實現進行了大量的研究，跟蹤性能也得到很大提升，但兩種方法都依然存在各自的問題。SMC實現方法對重要性函數的選取要求較高，并且粒子數過大導致計算復雜度增加，影響系統的實時性；GM實現方法要求線性高斯假設，目前的改進方法主要是通過近似處理非線性非高斯問題，但是以犧牲跟蹤精度為代價。有必要深入研究PHD遞推中的積分特性，探索新的處理解析運算和積分運算的方法，以達到運算復雜度和跟蹤精度的最優。

4.2 弱小多目標跟蹤

隨著軍事技術的發展，空中目標的運動速度、機動性和隱身性有了大幅度的提升，雷達等傳感器的檢測率降低，目標在傳感器上的成像一般都比較小，因此，研究弱小多目標跟蹤問題是一個研究重點和難點，雖然可以通過降低傳感器的檢測門限以提高目標的檢測概率，但隨之而來的是大量的虛警信息，基于PHD框架的PHD-TBD算法是一種有效的處理弱小多目標的方法，但該算法目前存在計算復雜度高，實時性較差的問題，需要對其進行深入的研究改進。

4.3 多傳感器多目標跟蹤

基于PHD濾波的多傳感器多目標跟蹤目前主要采用兩種方式，一種是多傳感器序貫處理方式，一種是多傳感器乘積PHD濾波方式。多傳感器序貫處理方式的優點在于執行簡單，計算復雜度小，但因傳感器順序的不同，跟蹤精度不同，這種方式對所有傳感器的數據融合層次較低，不能有效利用傳感器信息，跟蹤精度和穩定性差；多傳感器乘積PHD濾波對傳感器數據利用率高，跟蹤精度和穩定性較好，但計算復雜度較高，難以實現。因此，需要從原理及可行性上綜合考慮，構建多傳感器PHD多目標濾波器。

4.4 理論向實際應用轉化

目前，基于PHD的多目標跟蹤算法在理論上的研究已經取得了豐碩的成果，但廣大科研工作者大多利用模擬仿真環境進行研究，處理實際場景的研究較少，需要進行更多的研究來處理實際場景，同時在處理實際場景中發現問題，進而對算法進行深入研究。

［1］楊威，付耀文，龍建乾，等.基于有限集統計學理論的目標跟蹤技術研究綜述 ［J］. 電子學報 ，2012，7（40）：1440-1448.

［2］呂學斌，周群彪，陳正茂，等.高斯混合概率假設密度濾波器在多目標跟蹤中的應用［J］.計算機學報，2012，35（2）：397-404.

［3］徐洋.基于隨機有限集理論的多目標跟蹤技術研究［D］.長沙：國防科技大學，2012.

［4］MAHLER R P S.Multitarget bayes filtering via first-order multitarget moments［J］.IEEE Transactions on Aerospace and Electronic Systems，2003，39（4）：1152-1178.

［5］孟凡彬.基于隨機集理論的多目標跟蹤技術研究［D］.哈爾濱：哈爾濱工程大學，2010.

［6］楊峰，王永齊，梁彥，等.基于概率假設密度濾波方法的多目標跟蹤技術綜述［J］. 自動化學報，2013，39（11）：1944-1956.

［7］MAHLER R.PHD filters of higher order in target number［J］.IEEE Transactions on Aerospace and Electronic Systems，2007，43（4）：1523-1543.

［8］B N，MA W K.The gaussian mixture probability hypothesis density filter［J］.IEEE Transactions on Signal Processing，2006，54（11）：4091-4104.

［9］ZHENG X T，SONG L P.Improved CPHD filtering with unknown clutter rate ［C］// In：10th World Congress Conference on Intelligent Control and Automation，Beijing，2012：4326–4331.

［10］RISTIC B，CLARK D，VO B N，et al.Adaptive target birth intensity for PHD and CPHD filters ［J］.IEEE Trans.Aerosp.Electron.Syst.，2012，48（2）：1656-1668.

［11］PIECZYNSKI W.Pairwise Markov chains ［J］.IEEE Trans.Pattern Anal.Mach.Intell.，2003，25（5）：634-639.

［12］PIECZYNSKI W.Pairwise Markov chains and Bayesian unsupervised fusion［C］//Proc.3rd Int’l Conf.on Information Fusion，Paris，France，2000：10-13.

［13］PETETIN Y，DESBOUVRIES F.Bayesian multi-object filtering for pairwise Markov chains ［J］.IEEE Trans.Sign.Proc.，2013，61（18）：4481-4490.

［14］MAHLER R.Tracking targets with pairwise-markov dynamics ［C］//Proc.18th Int’l Conf.on Information Fusion，Washington，D.C.，2015：6-9.

［15］RONALD M，CONSULTANT E MN.On multitarget pairwise-Markov models［J］.SPIE，2015：9474.

［16］VO B T，VO B N，CANTONI A.Bayesian ltering with random nite set observations［J］.IEEE Trans.Signal Process.，2008，56（4）：1313-1326.

［17］TANG X，CHEN X，MICHAEL M，et al.A multiple-detection probability hypothesis density filter ［J］.IEEE Trans Signal Process，2015，63（8）：2007-2019.

［18］MAHLER R.CPHD and PHD filters for unknown backgrounds，II：Multitarget filtering in dynamic clutter［C］//Proc.SPIE 7330，2009.

［19］CHEN X，KIRUBARAJAN T，THARMARASA R，et al.Integrated clutter estimation and targettracking using spatial，amplitude，and Doppler information ［C］//Proc.SPIE 7697，2010.

［20］CHEN X，THARMARASA R，PELLETIER M，et al.Integrated clutter estimation and target tracking using Poisson point processes ［J］.IEEE Trans.AES，2012，48（2）：1210-1234.

［21］MAHLER R.Advances in statistical multisource-multitarget information fusion ［M］.Norwood，MA：Artech House，2014.

［22］MAHLER R，El-Fallah，A.ìCPHD and PHD filters for unknown backgrounds，III：Tractable multitarget filtering in dynamic clutter［C］//Proc.SPIE 7698，2010.

［23］MAHLER R，VO B T，VO B N，CPHD filtering with unknown clutter rate and detection profile ［J］.IEEE Trans.Sign.Proc.，2011，59（6）：3497-3513.

［24］MAHLER R，VO B T.An improved CPHD filter for unknown clutter backgrounds［C］//Proc.SPIE 9091，2014.

［25］MAHLER R.CPHD filters for unknown clutter and target-birth processes［C］//Proc.SPIE 9091，2014.

［26］VO B T，VO B N，HOSEINNEZHAD R，et al.Multi-bernoulli filtering with unknown clutter intensity and sensor field-of-view，Proc［C］//45th Conf.on Information Sciences and Systems（CISS2011），Baltimore，MD，2011：23-25.

［27］RONALD M，CONSULTANT，EAGAN，et al.Multi-bernoulli filtering with unknown clutter intensity and sensor field-of-view［C］//Proc.of SPIE，2011.

［28］VO B N，SINGH S，BOUCET A.Sequential monte carlo methods for multi-target filtering with random finite sets［J］.IEEE Transactions on Aerospace and Electronic Systems.2005，41（4）：1224-1245.

［29］VO M R.A theory of PHD filters of higher order in target number［C］//Proceedings of the 2006 Signal and Data Processing of Small Targets.Orlando，FL：SPIE，2006：62350K-62350K-12.

［30］LI T C，SUN S D，BOLI M，et al.Algorithm design for parallel implementation of the SMC-PHD filter［J］.Signal Processing，2016，119：115-127.

［31］YOON J H，DU Y K，YOON K J.Efficient importance sampling function design for sequential Monte Carlo PHD filter［J］.Signal Processing，2012，92：2315-2321.

［32］YOON K J，KIM D Y，YOON K J.Gaussian mixture importance sampling function for unscented SMC-PHD filter，Signal Processing，2013，93：2664-2670.

［33］ LI T C，SUN S D，Tariq Pervez Sattar.High-speed sigma-gating SMC-PHD filter ［J］.Signal Processing，2013，93：2586-2593.

［34］ZHANG H Q，GE H W，YANG J L，et al.A GM-PHD algorithm for multiple target tracking based on false alarm detection with irregular window ［J］.Signal Processing，2016，120：537-552.

［35］MAHDI Y D，ZOHREH A.Refined GM-PHD tracker for tracking targets in possible subsequent missed detections［J］.Signal Processing，2015，116：112-126.

［36］ WANG X，HAN C Z.An improved multiple model GM-PHD filter for maneuvering target tracking［J］.Chinese Journal of Aeronautics，2013，26（1）：179-185.

［37］ CLARK D， VO BT，VO BN.Gaussianparticle implementations of probability hypothesis density filters［C］//Proceedings of the 2007 IEEE Aerospace Conference，2007:1-11.

［38］周承興，劉貴喜，侯連勇，等.改進的高斯粒子概率假設密度濾波算法 ［J］. 控制理論與應用，2011，28（7）：1005-1008.

［39］LEHMANN F.Recursive bayesian filtering for multitarget track-before-detect in passive radars ［J］. IEEE Transactions on Aerospace and Electronic Systems，2012，48（3）：2458-2480.

［40］TONG H S，ZHANG H，MENG H D，et al.A shrinkage probability hypothesis density filter for multitarget tracking［J］.EURASIP Journal on Advances in Signal Processing 2011，116：1-13.

［41］HABTEMARIAM B K，THARMARASA R，KIRUBARAJAN T.PHD filter based track-before-detect for MIMO radars［J］.Signal Processing，2012，92：667-678.

［42］PUNITHAKUMAR K，KIRUBARAJAN T，SINHA A.A sequentialmonte carlo probability hypothesisdensity algorithm for multitarget track-before-detect ［C］//Proceedings of SPIE.San Diego，2005：1-8.

［43］ZHAN R H，GAO Y Z，HU J M，et al.SMC-PHD based multi-target track-before-detect with nonstandard point observations model［J］.J.Cent.South Univ，2015（22）：232-240.

［44］GRANSTRM K，LUNDQUIST C，ORGUNER U.Extended target tracking using a gaussian-mixture PHD filter［J］.IEEE Trans.Aerosp.Electron.Syst.，2012，48 （4）：3268-3286.

［45］MAHLER R.PHD filters for nonstandard targets，I：extended targets［C］//Proceedings of the 12th International Conference on Inf.Fusion，Seattle，WA，USA，2009：915-921.

［46］GRANSTRM K，ORGUNER U.On spawning and combination of extended/group targets modeled with random matrices［J］.IEEE Trans.Signal Process，2013，61（3）：678-692.

［47］LUNDQUIST C，GRANSTRM K，ORGUNER U.An extended target CPHD filter and a gamma Gaussian inverse Wishart implementation ［J］.IEEE J.Select.Topics Signal Process，2013，7（3）：472-483.

［48］ORGUNER U，LUNDQUIST C，GRANSTRM K.Extended target tracking with a cardinalized probability hypothesis density filter［C］//Proceedings of the 14th International Conference on Information Fusion，Chicago，Illinois，USA，2011：1-8.

［49］ZHANG Y Q，JI H B.A robust and fast partitioning algorithm for extended target tracking using a Gaussian inverse Wishart PHD filter［J］.Knowledge-Based Systems，2016（118）：1-17.

［50］CARPENTER G A，GROSSBERG S，ROSEN D B.Fuzzy ART：fast stable learning and categorization of analog patterns by an adaptive resonance system［J］.Neural Netw，1991，4（1）：759-771.

［51］GRANSTRM K，ORGUNER U.A PHD filter for tracking multiple extended targets using random matrices［J］.IEEE Trans.Signal Process，2012，60（11）：5657-5671.

［52］MAHLER R.Approximate multisensor CPHD and PHD filters［C］//Proceedings of the 13th International Conference on Information Fusion，Edinburgh，Scotland，2010：1-8.

［53］ MAHLER R.The multisensor PHD filter，I：general solution via multitarget calculus［C］//Proceedings of the SPIE Conference on Signal Processing，Sensor Fusion and Target Recognition，2009：1-12.

［54］MAHLER R，EL-FALLAH A.Bayesian unified registration and tracking［C］//Proceedings of the SPIE Conference on Signal Processing，Sensor Fusion and Target Recognition，2011：1-11.

［55］LI W，JIA Y，DU J，et al.Gaussian mixture PHD filter for multi-sensor multi-target tracking with registration errors［J］.Signal Process，2013，93（1）：86-99.

［56］LIAN F，HAN C，LIU W，et al.Joint spatial registration an multitarget tracking using an extended probability hypothesis density filter ［J］.IET Radar Sonar Navig，2011，5（4）：441-448.

［57］DELANDE E，DUFLOS E，VANHEEGHE P，et al.Mul-ti-sensor PHD by space partitioning：computation of a true reference density within the PHD framework［C］//Proceedings of the IEEE International Conference on Statistical Signal Processing Workshop，Nice，2011：333-336.

［58］LIU L，JI H B，FAN Z H.Improved Iterated-corrector PHD with Gaussian mixture implementation［J］.Signal Processing，2015，114：89-99.

［59］LI W L，JIA Y M，DU J P，et al.Gaussian mixture PHD filter for multi-sensor multi-target tracking with registration errors［J］.Signal Processing，2013，93：86-99.

［60］ WU W H，JIANG J，LIU W J，et al.Augmented state GM-PHD filter with registration errors for multi-target tracking by Doppler radars ［J］.Signal Processing，2016，120：117-128.