基于多步新息的機(jī)動檢測方法

王 勇

（江蘇自動化研究所，江蘇 連云港 222061）

0 引言

機(jī)動目標(biāo)跟蹤主要包括觀測數(shù)據(jù)預(yù)處理、機(jī)動目標(biāo)模型、機(jī)動檢測與機(jī)動辨識、濾波與預(yù)測以及跟蹤坐標(biāo)系和濾波狀態(tài)變量（即目標(biāo)空間位置定位與描述）的選取等。其困難主要來源于兩個方面：一是目標(biāo)運動的不確定，二是觀測數(shù)據(jù)的噪聲。要解決此困難，一個重要的環(huán)節(jié)就是機(jī)動檢測［1-3］。

機(jī)動檢測的主要思想是根據(jù)觀測量Y（k）與狀態(tài)預(yù)測量（）構(gòu)成的新息向量 d（k）=Y（k）－的變化情況，按照某一準(zhǔn)則或者邏輯進(jìn)行機(jī)動檢驗。基于機(jī)動檢測結(jié)果，自適應(yīng)調(diào)整系統(tǒng)狀態(tài)噪聲陣或濾波增益，對機(jī)動目標(biāo)的運動狀態(tài)進(jìn)行濾波估計和預(yù)測，從而實現(xiàn)對機(jī)動目標(biāo)的跟蹤功能。因此，可靠及時地檢測出目標(biāo)機(jī)動模式直接影響機(jī)動目標(biāo)跟蹤的性能。

進(jìn)入21世紀(jì)后，由于電子技術(shù)的快速發(fā)展，反艦導(dǎo)彈性能有了大幅度提高。末端防御系統(tǒng)為了提高對反艦導(dǎo)彈的處理能力，一種方法是提高火控系統(tǒng)數(shù)據(jù)率，以充分使用跟蹤器的目標(biāo)量測數(shù)據(jù)，提高對超音速反艦導(dǎo)彈的解算處理能力。針對系統(tǒng)數(shù)據(jù)率提高，傳統(tǒng)的基于新息的機(jī)動檢測方法［4-7］不再適用。為此，本文提出了一種基于多步新息的機(jī)動檢測方法，可較好地提取出目標(biāo)機(jī)動信息，便于機(jī)動檢測，并通過仿真計算，對于給定虛警率，針對基于衰減記憶的機(jī)動檢測方法，給出最小機(jī)動檢測延遲與衰減系數(shù)的關(guān)系。

1 多步新息計算方法

目標(biāo)動態(tài)模型用來描述目標(biāo)狀態(tài)X關(guān)于時間的變化情況。常用的是狀態(tài)空間線性模型（連續(xù)時間模型）為：

或離散時間模型為：

以離散狀態(tài)方程為例，X（k）、Y（k）和 U（k）分別是目標(biāo)狀態(tài)、觀測和控制輸入在k時刻的向量；Φ（k+1，k）和H（k）分別是適當(dāng)維的系統(tǒng)狀態(tài)轉(zhuǎn)移矩陣和觀測矩陣；W（k）和V（k）分別是系統(tǒng)模型噪聲和觀測噪聲，且噪聲W（k）和V（k）為互不相關(guān)的高斯白噪聲序列，其統(tǒng)計特性為：

其中，Q、R分別為系統(tǒng)噪聲和觀測噪聲協(xié)方差矩陣［8-9］。

新息為觀測量與預(yù)測之間的差值，其公式表示為：

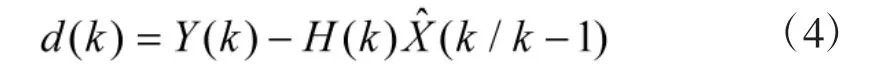
文獻(xiàn)［4］證明了以卡爾曼濾波與預(yù)測為載體的線性最優(yōu)濾波新息序列具有零均值高斯白噪聲特性。

多步新息是指利用觀測量Y（k）與狀態(tài)變量的T步預(yù)測量計算的差值{dT（k）}：

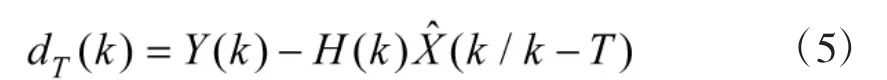
這里，T為系統(tǒng)運行周期的整數(shù)倍。如果目標(biāo)沒有作機(jī)動，對非機(jī)動目標(biāo)模型來說，dT（k）同樣具有零均值高斯白噪聲特性，本文所描述的機(jī)動檢測方法也是基于該特性。

2 機(jī)動檢測方法

檢測目標(biāo)是否機(jī)動是一個決策問題，可以公式化為假設(shè)檢驗問題：

H0：目標(biāo)非機(jī)動；H1：目標(biāo)機(jī)動

根據(jù)觀測殘差和控制輸入的特性，在機(jī)動目標(biāo)跟蹤中，很多機(jī)動檢測使用χ2檢驗或準(zhǔn)χ2檢驗，即在H0（檢測機(jī)動開始）條件下，檢測估計的統(tǒng)計量是否服從χ2分布。假設(shè)在H0條件下ε服從自由度為n 的 χ2分布（ε～χn2），且下式成立，則表明目標(biāo)開始機(jī)動。

這里1－α是置信度。

歸一化殘差平方為。

為減少虛警和漏警的概率發(fā)生，這里采用衰減記憶統(tǒng)計量方法進(jìn)行假設(shè)檢驗，記衰減記憶和為εkρ。

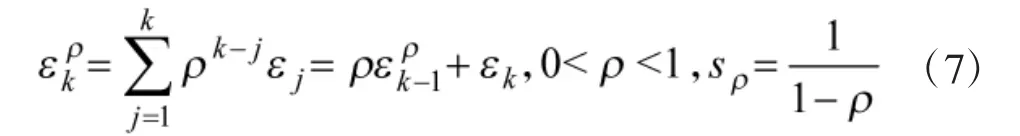
其中，ρ為衰減系數(shù)，sρ為衰減記憶和的等效窗口長度。因為 εk服從自由度為 n 的 χ2分布（即（εk～χn2，n=dim（d））。作為高斯變量的加權(quán)和 εkρ并不服從 χ2分布，但通過權(quán)匹配可將它近似看作χ2變量，即近似認(rèn)為［10］

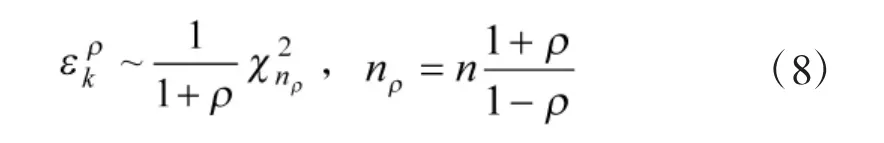
實際應(yīng)用中，在球坐標(biāo)系下跟蹤時n=3。至此，可根據(jù)式（7）來檢測機(jī)動起始，其中 ε=εkρ。

3 機(jī)動檢測延遲時間

通常對假設(shè)檢驗問題希望獲取盡可能多的測量值來提高檢測概率。但對機(jī)動檢測問題來說，希望盡可能快地獲得判定，即獲得判定的延遲最小。這樣就面對兩種互為矛盾的目標(biāo)，即為增加檢測概率而試圖延遲判定，與此同時試圖減小延遲來避免跟蹤滯后。所以，在固定虛警率下能夠準(zhǔn)確地獲取機(jī)動檢測延遲時間是至關(guān)重要的。

根據(jù)式（7），可以看出εkρ的計算值與機(jī)動幅度（新息值）和窗口長度（sρ）有關(guān)，即基于 χ2檢驗的機(jī)動檢測延遲時間是系統(tǒng)機(jī)動模型、機(jī)動幅度、門限值（α）和窗口長度（等價于衰減系數(shù)ρ的大小）的函數(shù)。基于多步新息的機(jī)動檢測延遲時間則是系統(tǒng)機(jī)動模型、機(jī)動幅度（與步長也有關(guān)系）、置信度和窗口長度的函數(shù)。

置信度是根據(jù)系統(tǒng)要求給定的，如果選取α值較小，即置信度較高，即判定目標(biāo)機(jī)動的門限值較高，因此，檢測機(jī)動的延遲就大。所以，α值與機(jī)動檢測延遲成反比關(guān)系。機(jī)動幅度也影響檢測延遲，大機(jī)動使得新息序列的值較大，于是統(tǒng)計值εkρ有較大的數(shù)值。對于固定的檢測門限，能更早地檢測到機(jī)動。實際應(yīng)用中，由于目標(biāo)是未知的，從而機(jī)動幅度也是事先未知的，不能用于系統(tǒng)優(yōu)化。當(dāng)窗口長度 sρ較大時，εkρ/sρ的隨機(jī)性很弱，檢測滯后較大；同時若多步新息的步長較大，同樣會帶來檢測滯后，所以多步新息的步長選擇，以及窗口長度（衰減系數(shù)）的選擇能優(yōu)化系統(tǒng)。

4 仿真分析

考慮到最優(yōu)問題的復(fù)雜性，這里采用仿真計算的方法，以指導(dǎo)步長和衰減系數(shù)的選擇。

目標(biāo)仿真航路是從勻速直線過渡到以某個固定過載做勻加速運動，共仿真5條目標(biāo)航路，目標(biāo)過載能力從1.0 g到5.0 g。對每條航路選擇衰減系數(shù)從0.1到0.8不等。不同過載條件下，最小檢測延遲時間與衰減系數(shù)的關(guān)系如圖1所示。可以看出衰減系數(shù)越小，最小檢測延遲時間越長，這也與理論分析是一致的。

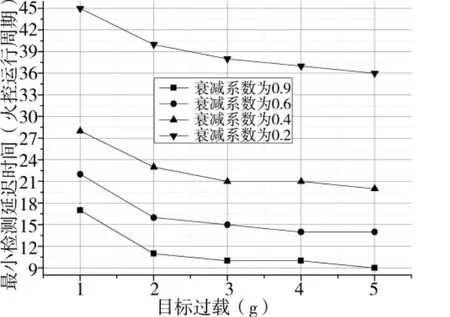
圖1 最小檢測延遲時間與衰減系數(shù)的關(guān)系

對以上每個航路在固定衰減系數(shù)時，將多步新息的步長從10設(shè)置到60（火控運行周期的倍數(shù)）不等，并進(jìn)行仿真計算。仿真結(jié)果表明：對于有顯著機(jī)動的目標(biāo)航路（如本文設(shè)計的那樣），不同步長下的機(jī)動檢測延遲時間沒有變化，如表1所示；但可以顯著降低目標(biāo)機(jī)動檢測的虛警率，如圖2所示。

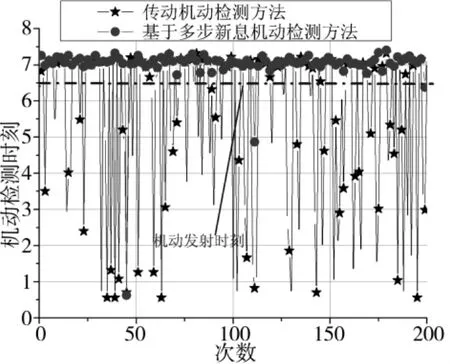
圖2 基于多步新息檢測方法與傳統(tǒng)機(jī)動檢測方法對比

在衰減系數(shù)為0.2時，不同航路、不同步長下的最小機(jī)動檢測延遲時間如表1所示。

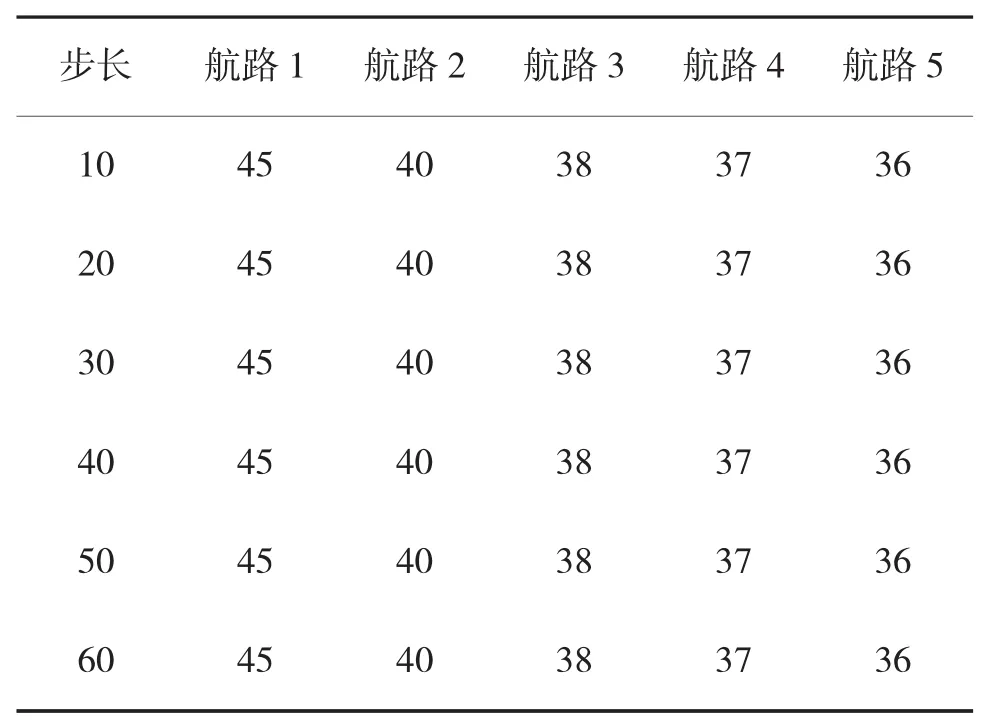
表1 固定衰減系數(shù)下，不同航路、不同步長下的最小機(jī)動檢測延遲時間（火控運行時間）

針對弱機(jī)動航路，同樣是從勻速直線過渡到以某個固定過載做勻加速運動，但目標(biāo)過載只有0.2 g。在固定衰減系數(shù)條件下，最小檢測延遲時間與步長的關(guān)系如圖3所示。可以看出對于固定衰減系數(shù)，存在最優(yōu)的預(yù)測步長。

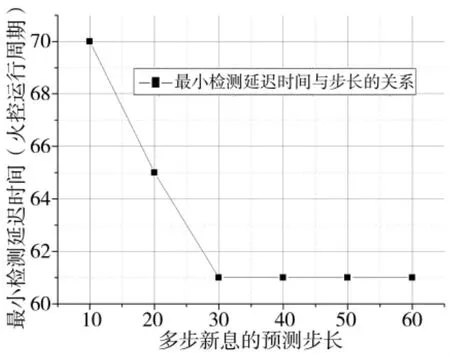
圖3 最小檢測延遲時間與多步新息預(yù)測步長的關(guān)系

5 結(jié)論

反艦導(dǎo)彈一個重要的發(fā)展方向是速度越來越快，留給末端防御系統(tǒng)的反應(yīng)時間越來越短。為提高對反艦導(dǎo)彈的處理能力，一個有效的方法是提高防御系統(tǒng)對跟蹤數(shù)據(jù)的使用率，即提高末端防御系統(tǒng)的數(shù)據(jù)率。但數(shù)據(jù)率的提高會降低傳統(tǒng)基于單步新息機(jī)動檢測窗口的信噪比。基于此，本文提出了基于多步新息的機(jī)動檢測方法，并采用基于衰減記憶的機(jī)動檢測方法。針對給定的機(jī)動檢測門限，通過分析和仿真表明：基于多步新息機(jī)動檢測方法可以顯著降低虛警率。針對仿真航路，同時給出了最小檢測延遲時間與衰減系數(shù)，以及與預(yù)測步長的關(guān)系。

［1］徐國亮.機(jī)動目標(biāo)跟蹤算法［J］.情報指揮控制系統(tǒng)與仿真技術(shù)，2002，30（8）：42-56.

［2］石章松，謝君.機(jī)動檢測算法特性分析仿真研究［J］.計算機(jī)仿真，2007，24（9）：90-94.

［3］高超，鄧曉波.高速機(jī)動目標(biāo)檢測算法研究［J］.計算機(jī)仿真，2014，31（12）：1-5.

［4］姚洪利，高效，田科鈺.基于衰減記憶n次新息的目標(biāo)機(jī)動檢測和排飛點［J］.情報指揮控制系統(tǒng)與仿真技術(shù)，2004，26（5）：25-29.

［5］宋驪平，姬紅兵，高新波.基于高階累積量的目標(biāo)機(jī)動檢測新方法［J］.電子學(xué)報，2004，32（1）：154-156.

［6］李海，吳仁彪，王小寒.基于非線性最小二乘的空中機(jī)動目標(biāo)檢測方法 ［J］.電子與信息學(xué)報，2012，34（9）：2143-2147.

［7］尚海燕，張雅斌，蘇洪濤，等.長觀測時間內(nèi)機(jī)動目標(biāo)檢測方法 ［J］.系統(tǒng)工程與電子技術(shù) ，2006，28（12）：1779-1782.

［8］張蕊，史麗楠.基于擴(kuò)展卡爾曼濾波的機(jī)動目標(biāo)跟蹤研究［J］.航天控制，2012，30（3）：12-17.

［9］岳帥，孔令講，楊建宇，等.卡爾曼動態(tài)規(guī)劃機(jī)動目標(biāo)檢測前跟蹤方法［J］.現(xiàn)代雷達(dá)，2011，33（6）：58-63.

［10］徐國亮，鄧雅娟.機(jī)動目標(biāo)建模及機(jī)動檢測算法［J］.情報指揮控制系統(tǒng)與仿真技術(shù)，2005，27（4）：81-83.