基于高斯函數加權的自適應KNN算法
李昂
(上海海事大學,上海 201306)
0 引言
K近鄰(K-Nearest Neighbor,KNN)算法由 Cover和Hart在1967年首次提出[1]。作為最古老的、最簡單的模式識別算法之一,KNN算法在信息檢索、機器學習和自然語言處理領域都有廣泛的應用[2]。傳統KNN算法的主要思想是:在對一個樣本點進行分類處理時,首先找到與給樣本點最相似的k個鄰居樣本點,統計分析這k個樣本點的類別標簽,將出現次數最多的類別標簽作為待分類樣本點的類別。同時,考慮到不同的鄰居樣本點距離待分類樣本點的相似程度,為每一個鄰居樣本點分配各自的權重,以調節其對分類結果的影響程度。一般地,采用歐氏距離來量化兩個樣本點之間的相似程度。距離越遠表示相似度越小,所占權重越小,反之,距離越小表明相似度越大,所占權重越大。
傳統KNN算法的思路簡單直觀、易于快速實現。但是其通常為每一個待分類的樣本點分配一個相同的k值,這種做法只在樣本點在各個類別間均勻分布時才有較顯著的分類效果。在實際應用環境中經常出現分布不均勻的數據集,樣本點往往集中于某一個或者某幾個類別中,傳統的KNN算法在這種情況下往往會失去優勢[3]-[5]。由此可見,k值的選取是KNN算法能否正確分類的一個關鍵。對于不同的樣本點,根據其自身數據特點自適應地選取k值是本文的研究重點。
為了提升傳統KNN算法在不平衡數據集分類中的準確度,最優k值的選取一直以來被廣泛關注,大部分的理論工作集中于為每一個待分類的數據集找到最優的k值,但是忽略了數據集的具體結構和需要分類的樣本點的基本屬性[6]。例如,Samworth針對KNN算法提出了最優權重向量的最優表達式,同時可以求出數據集的最優鄰居數[7]。但是這個結果只在數據集中化的樣本點趨于無窮大是才能夠成立;對于基于內核的方法,也存在幾種適應性地選擇內核帶寬(等價于k值)方案[8-11]。但是在實際應用中,對內核函數的選擇沒有原則性的方法。此外,上述對于權重以及k值的選取在給定數據集下,對于所有的待分類樣本點都是相同的,并沒有針對具體數據集內樣本點的具體分布情況,為每一個樣本點分配最優的k值[12-14]。2010年Sun等人針對該問題提出了一種自適應的k值選取方法,選用距離最近鄰居樣本點的k值作為自己的最優鄰居數[3]。這種方案思路簡單易于實現,并且可以做到自適應的為每個樣本點選取k值,但是由于方案沒有充分考慮到樣本點分布不平衡的問題,導致分類結果會出現一定的誤差。2017年,Anava等人提出了一種自適應的KNN算法,可以為每個樣本點自適應的計算權重向量和k值,但是該算法在同時計算出權重向量和k值的同時需要消耗大量的計算資源[6]。
本文在Sun等人的基礎上,對自適應的KNN算法進行了改進,充分考慮到數據集內樣本點的具體分布和計算資源的消耗,提出了一種輕量級的自適應k值計算方案。并且通過實驗驗證了該算法的分類準確率和計算效率。實驗表明輕量級的自適應KNN算法在準確率和計算效率方面較以往算法有一定的提高。
1 預備知識
1.1 系統建模
將一個分類算法抽象為系統參數(k,w,ω)、類別標簽集Y、樣本分類函數Y、距離函數d、樣本判別函數c、訓練樣本集 Xtrain、待分類樣本集 Xclassify。其定義如下:
●系統參數(k,w,ω)中k表示某一個樣本點X的最近鄰個數;分量權重向量w=(w1,w2,…,wn)分別表示在計算距離時,樣本點向量X每一個維度的權重值;距離權重向量 ω=(ω1,ω2,…,ωn)表示某一樣本點 X 的最近鄰集合中每個樣本點的權重。
●用一個n維向量X=(x1,x2,…,xn)表示一個樣本點,它是KNN分類算法的基本單位。對于某一個樣本點Xi來說,kNNXi={X1,X2,…,Xk}表示的是與Xi最近的k個鄰居樣本點的集合。
●類別標簽集Y={y1,y2,…,ym}是系統中的所有類別標簽的集合,yi是其中第i個標簽的標號。
●樣本分類函數Y:Rn→R用來給出某一樣本點的類別標簽。對于一個待分類的樣本點Xi,其分類結果可以表示為:
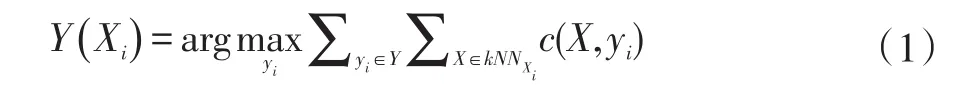
若Y(X)=yi表示樣本點X對應的類別標簽為yi;特別地,若某樣本X的類別標簽未被確定,則Y(X)=⊥。
●距離函數d:Rn×Rn→R用于計算兩個樣本點之間的距離,一般地,取歐氏距離d(Xi,Xj)=作為兩個樣本點之間的距離測度。其中Xi,Xj是兩個不同的樣本點,wr是樣本點向量第r維的權重。
●樣本判別函數c:Rn×N→{0,1}用于判斷樣本點是否屬于某一類別,若c(X ,yi)=1表示樣本點X屬于類別 yi,若 c(X ,yi)=0則表示樣本點X不屬于類別yi,其中i=1,2,…,m。
●訓練樣本集Xtrain={X|Y(X )≠⊥}是一個類別標簽已知的樣本點集合。
●待測樣本集Xclassify={X|Y()X=⊥}是一個類別標簽未知的樣本點集合。
1.2 傳統的KNN算法
由于具有簡單直觀的特點,因此傳統KNN算法是目前應用最廣泛的模式識別算法之一。對于一個特定的數據集,通過交叉驗證的方法為整個系統中的每一樣本點設置統一的k值。一個標準的KNN分類算法的步驟如下:
(1)輸入包含M個樣本點的訓練樣本集Xtrain,通過交叉驗證法確定系統參數k;
(2)輸入包含N個樣本點待測樣本集Xclassify,對于Xclassify每一個樣本點X,運用距離函數d計算其與訓練樣本集Xtrain每一個樣本點的距離矩陣其中,dij表示第i個待測樣本與第 j個訓練樣本的歐氏距離。
(3)依 次 遍 歷 距 離 矩 陣DN×M的 行 向 量(di1,di2,…,diM)并根據大小進行排序,選擇距離最小的k個距離記錄其下標。
(4)對于一個每待測樣本點Xi,根據(3)中記錄的最近鄰下標,取其最近的k個訓練樣本點,構成Xi的最近鄰集合kNNXi?Xtrain。
(5)根據式(1)對樣本點Xi的分類進行預測,記錄分類結果Y(Xi);重復(4)和(5)直至所有樣本分類完畢。
(6)統計分類結果并分析正確率。
這種為所有的樣本點設置固定的k值的做法的前提是所有的待測樣本點均勻分布在各個類別的數據集中。在樣本點分布不平衡的數據集中,不同類別之間樣本點的個數差別較大。這在種情況下,如果為每一個待測樣本點都分配相同的k值,很可能要大于該類別內的樣本點總數,分類結果會受到嚴重的偏差。因此,根據每個待測樣本點的分布特點為其分布合適的k值可以大大提高KNN算法的準確度。
2 基于高斯函數加權的自適應KNN算法
為了適應不平衡的數據集,需要根據樣本點在樣本空間中的分布情況為每一個樣本點自適應的設置k值。基于高斯函數加權的自適應KNN算法利用高斯函數計算距離權值向量ω,并根據ω計算樣本點的自適應最近鄰個數k。自適應的k值計算分為兩個部分,一是為訓練樣本集Xtrain中的每一個訓練樣本點計算合適的最近鄰個數kj;二是根據Xtrain中各個樣本點的最近鄰個數ki,計算待測樣本集Xclassify中樣本點的最鄰個數k。i
2.1 訓練樣本點 k值計算
在一個容量為M的訓練樣本集Xtrain中,為了確定某樣本點的最優近鄰個數kj,需要計算與其他M-1個樣本點的歐氏距離為了降低計算復雜度,算法規定最近鄰個數k∈[1,9]。因此只取與樣本點最近的9個鄰居樣本點,構成最近鄰集合隨后根據式(2)計算鄰居樣本點的距離權值,得出的權值向量距離權值計算方式如下:
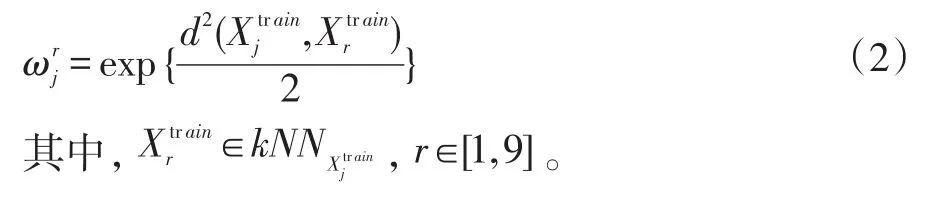
對于 kj,r∈[1,9],根據式(3)計算最近鄰個數 k的概率分布:
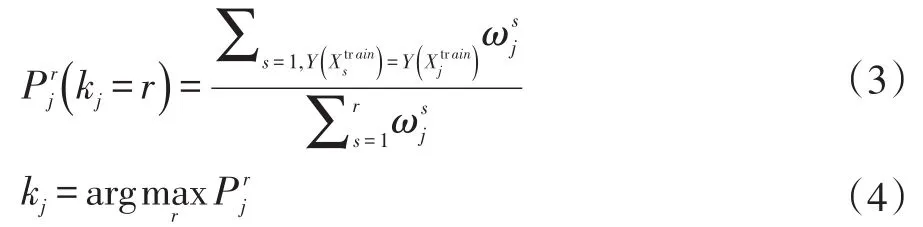
訓練樣本的最優鄰居數kj由式(4)確定,即選擇概率最大的最近鄰個數。算法1給出了計算訓練樣本點最近鄰個數的具體步驟。
2.2 待測樣本點k值計算
在一個容量為N的訓練樣本集Xclassify中,為了確定某樣本點的最優近鄰個數ki,首先計算與M個訓練樣本點的歐氏距離同樣取與樣本點最近的9個鄰居樣本點,構成最近鄰集合向量的分量表示最近鄰集合對應樣本點的最優近鄰個數,k可由式(4)計算得出。根據式(5)計算的權值向量其中則待測樣本點的最優近鄰個數可以根據式(6)確定。
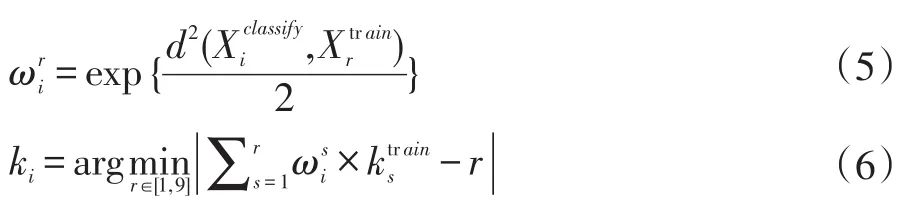
算法1計算訓練樣本k值

最后,根據式(1)對樣本點Xi的分類進行預測,記錄分類結果Y(Xi)。算法2給出了計算待分樣本點最近鄰個數的具體步驟。
算法2計算待測樣本k值
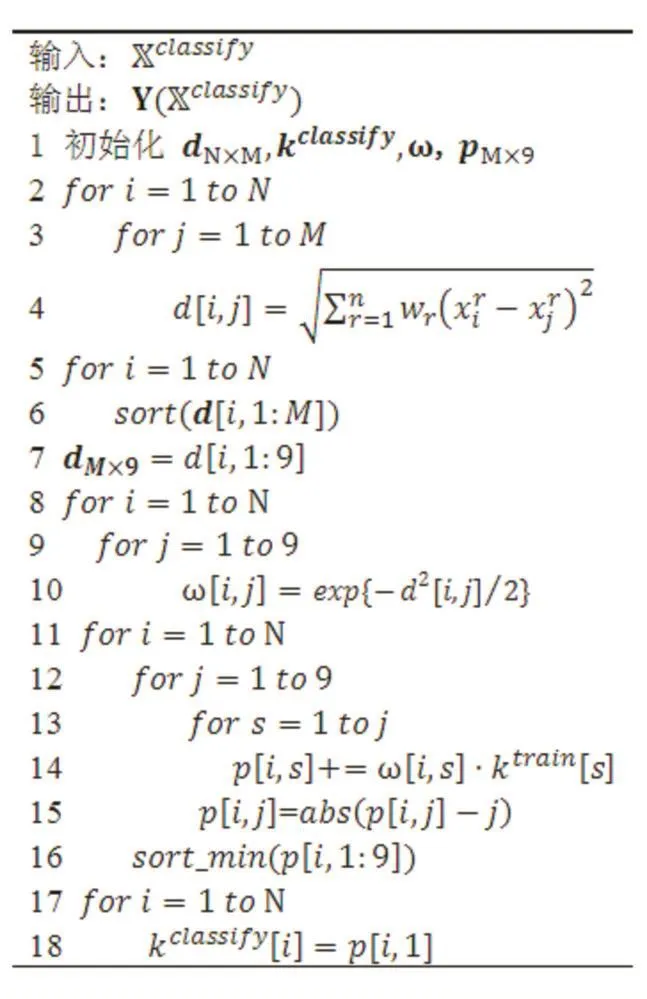
3 實驗結果
為了驗證本文算法的有效性,我們設計實驗,將本文算法的分類準確率與傳統KNN算法[1]、典型的Nada?rays-Watson算法[11]比較。
3.1 實驗平臺與實驗數據
算法的測試平臺為Windows 10,測試環境為測試環境為CPU Intel Core i5-7200U 2.50GHz,內存8GB的PC,用JupyterNotebook實現。
本文選取了10組UCI數據集(https://archive.ics.uci.edu/ml/machine-learning-databases)作為驗證集。對于每個數據集,隨機取90%的樣本作為訓練集,另外10%的樣本作為待測樣本集。在每個數據集中,樣本數據都是由數值組成。表1中前5個數據集(Iono?sphere,Parkinsons,Pima,Haber,Blood)為 二 元 分 類yi∈{0,1},后5個為多元分類。表1顯示了實驗數據分布情況。
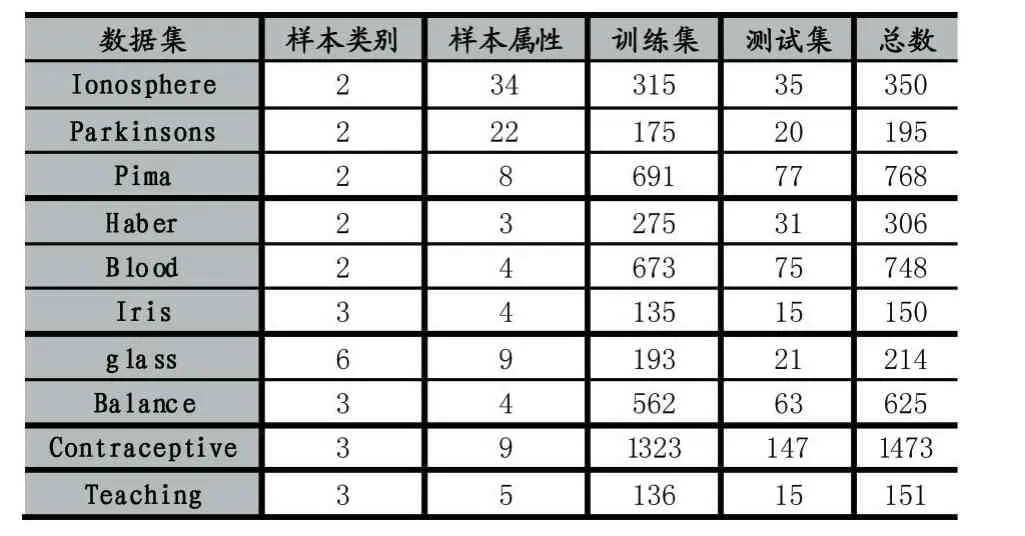
表1 實驗數據分布
3.2 實驗步驟
(1)選擇樣本:輸入樣本數為N的數據集,隨機選擇其中90%為訓練集,剩下的10%為測試集。對于每個樣本集,得到10個訓練集與10個測試集。
(2)標準kNN算法和Nadarays-Watson算法:在(1)中得到的10個測試集上進行標準的kNN算法以及Nadarays-Watson算法。
(3)得到每個樣本的最優k值:對于每個訓練集運用算法1,計算得出訓練集中每個樣本的最優k。
(4)自適應的KNN算法:由(3)中得出的最優k,在(1)中得出的測試集中進行算法2。
(5)計算上述3種算法中10個測試集的平均準確率。
(6)比較(5)中得到的不同的結果。
3.3 實驗結果
按照3.2中的步驟進行實驗,所得的三類算法的準確度在表2和表3中顯示。
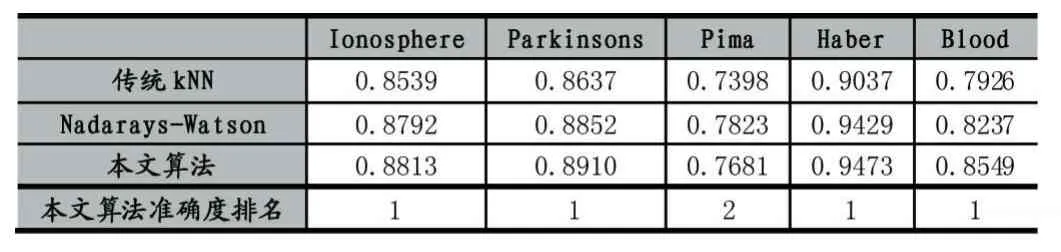
表2 算法的準確度比較(前5個數據集)
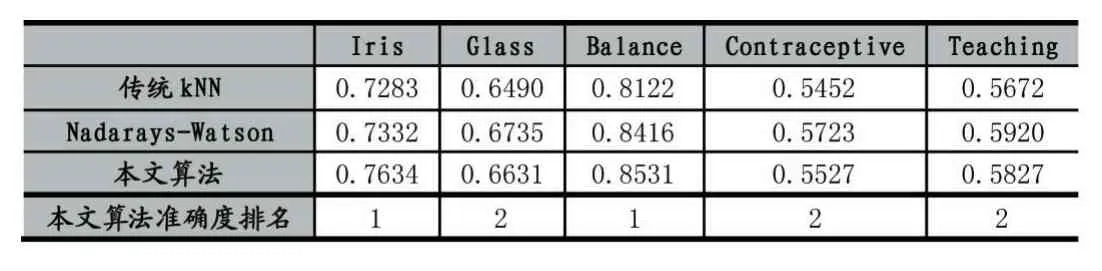
表3 算法的準確度比較(后5個數據集)
從實驗結果可以看出1)本文相較于傳統的KNN算法有更高的準確度,并且在其中6個數據集中準確度高于Nadarays-Watson算法。其中在數據集Haber中準確度最高,在數據集Contraceptive中準確度最低;2)對比表2和表3可以得出,與多元分類相比,KNN算法在二元分類中的準確度較高。
4 結語
本文在Sun等人的基礎上,針對待分類數據分布不均的情況,提出了一種基于高斯函數加權的自適應KNN算法。該算法能過根據樣本點的分布情況自適應的為每個樣本點分配最近鄰個數(k值)。實驗結果表明,該算法相較傳統的KNN算法與基于核函數的Nadarays-Watson算法在分類精度上具有明顯的優勢。
[1]COVER M,HART P.E.Nearest Neighbor Pattern Classification.IEEE Transactions on Information Theory,13(1):21-27,1967.
[2]毋雪雁,王水花,張煜東.K最近鄰算法理論與應用綜述[J].計算機工程與應用,2017,53(21):1-7.
[3]SUN S,HUANG R.An Adaptive K-Nearest Neighbor Algorithm[C].Seventh International Conference on Fuzzy Systems and Knowledge Discovery.IEEE,2010:91-94.
[4]王超學,潘正茂,馬春森等.改進型加權KNN算法的不平衡數據集分類[J].計算機工程,2012,38(20):160-163.
[5]GHOSH A K.On Optimum Choice of k in Nearest Neighbor Classification[J].Computational Statistics&Data Analysis,2006,50(11):3113-3123.
[6]ANAVA O,KFIR Y.L.k*-Nearest Neighbors:From Global to Local[C].Advances in Neural Information Processing Systems.2016:1-16.
[7]SAMWORTH R.J.Optimal Weighted Nearest Neighbour Classifiers.The Annals of Statistics,2011,40(5):2733-2763.
[8]ABRAMSON I S.On Bandwidth Variation in Kernel Estimates-A Square Root Law[J].Annals of Statistics,1982,10(4):1217-1223.
[9]SLIVERMAN B.W.Density Estimation for Statistics and Data Analysis,Volume 26.CRC press,1986.
[10]DEMIR S,TOKTAMIS ?.On the Adaptive Nadaraya-Watson Kernel Regression Estimators[J].Hacettepe University Bulletin of Natural Sciences&Engineering,2010,39(3):429-437.
[11]KHULOOD H A,LUTFIAH I A T.Modification of the Adaptive Nadaraya-Watson Kernel Regression Estimator[J].Scientific Research&Essays,2014,9(22):966-971.
[12]KULIS B.Metric Learning:A Survey[J].Foundations&Trends? in Machine Learning,2013,5(4).
[13]BIAU G,DEVROYE L.Lectures on the Nearest Neighbor Method[M].Springer International Publishing,2015.
[14]HASTIE T,TIBSHIRANI R.Discriminant Adaptive Nearest Neighbor Classification[J].IEEE Transactions on Pattern Analysis&Machine Intelligence,1996,18(6):607-616.

