例談物理驗證中舍解的依據與意義
李桂旺
(江蘇省前黃高級中學,江蘇 常州 213161)
隨著科學技術的發展,要求培養出善于創新的復合型人才,這就要求教師對學生進行物理科學素質及學科滲透能力的培養.應用數學處理物理問題的能力是物理學科的關鍵能力要求,也是分析與解決問題的重要手段之一.
數學是解決物理問題的重要工具,在利用數學工具解決問題中我們常常要求對分析的結論進行驗證,以確定結論的科學性與合理性.數學的多解也是物理問題中比較常見的情形,但數學的多解不一定有物理意義或都合理,如何排除不合理的數學解是平時教學過程中需要關注.也就是對最后形成的結論進行論證,沒有物理意義的“解”需要舍去,從而排除這種“物理不可能”,使結論更具科學性.
1 規律的持續性
物理情景中,事件的發展的過程所遵循的規律有時并不單一.由于物理過程所遵循規律的變化從而致使部分“結論”無“意義”,此解應當舍去.同時也需要研究變化后的新規律對應的結論.
例1.一輛汽車沿水平路面以速度108km/h正常行駛.司機由于特殊原因進行急剎車(不考慮反應時間),則剎車后汽車前進72m需要多長時間?(已知汽車與與水平路面的摩擦因數為μ=0.6,g=10m/s2)
解析:對勻變速運動規律應用比較熟悉的同學,遇到這種類型的問題應對相對輕松.但對剛學習這部分內容的學生,通常是按部就班利用勻變速直線運動規律來分析解決問題.
其中v0=108km/h=30m/s,a=μg=-6m/s2,即
得t1=4s或t2=6s(舍去).
舍解的依據:此情涉及到交通工具剎車類問題,應用規律時是簡單套用勻變速直線運動規律.實際模型是,汽車剎車后僅需要t0=v0/a=5s時間停止,故t2=6s的解應該舍去.此類問題習慣稱為“交通工具剎車類”問題.
被舍解的意義:實際上直接運用勻變速運動規律是誤以為汽車剎車后一直勻變速直線運動,即全程加速度一直不變化的運動,此解為“返程”時到達72m處時的時間.通過判斷發現,汽車停止后就不會再回頭加速運動.
2 時間的方向性
在勻變速直線運動中物體(質點)的位移是時間的二次函數,當涉及到時間時,一般是兩解.此時就需要驗證兩解是否都有意義.
例2.已知某住宅樓三樓空調外機安裝平臺高6米.某工人在該平臺以初速度5.0m/s豎直向上拋出一個物體(拋出時手伸在平臺外側,下方是安全區域).則需要多長時間物體可到達拋出點下方3.75m處?(不考慮阻力且重力加速度g=10m/s2)
解析:本題是豎直上拋運動規律的應用.直接利用勻變速直線運動規律.取向上為正方向
得t1=1.5s和t2=-0.5s(舍去).
舍解的依據:因為時間的變化是有方向性的,物體是沿時間變化的方向發生位置變化的.而聯立方程時取拋出點為計時0時刻,即此后的時刻才符合要求.
被舍解的意義:從物理角度看時間“負”值,其物理意義應該表示“過去”,即t2表示拋出之前的0.5s時.之所以數學上有解,是因為方程只能呈現位移與時間的關系無法體現時間發展的方向性.即可將這個物體的運動曾經(-0.5s時)出現在該位置,中途(0時刻)經過了拋出點后再經過1.5s時通過該位置.
3 潛在條件約束
在事物發展變化過程中原本就會可能出現多解的情況,因特定條件下約束從而舍解.這類條件有可能是顯性的也可能是隱性的,解析過程中要將其轉化為數學條件而限制.
例3.已知某住宅樓三樓空調外機安裝平臺高6m.某工人在該平臺以初速度5.0m/s豎直向上拋出一個物體(拋出時手伸在平臺外側,下方是安全區域).則需要多長時間物體距離平臺3.75m?(不考慮阻力且重力加速度g=10m/s2)
解析:粗看上去這題與例2似乎相同,仔細審題發現區別在問題上.在例1中明確指出物體在拋出點下方的位置,而本題中沒有這個要求,自然需要考慮上方的情況.
與例2同理.取向上為正方向有方程
因為Δ<0,所以沒有數學解.
舍解的依據:通過條件約束判斷發現,物體上升的最高點H=1.25m,不可能出現在上方3.75m處.
被舍解的意義:此討論的“解”是一種分析過程,審題過程中是需要考慮到這種情型存在的可能性.只能通過定量分析通過數學解去否定了這種情型.如果試確定距離拋出點1m處需要的時間,上方的情型“解”就物理意義.

圖1
進階:如圖1所示,現有一單面長度為24m的水平傳送帶,以22m/s速度逆時針勻速運轉.在傳送帶左端一小物體(可以看著質點)以20m/s初速度向右滑行,物體與傳送帶間的摩擦因數為0.8.則物體發生位移20m需要多長時間?(
g
=10m/s
2
)
解析:若單純看這個問題其實就是勻變速直線運動規律的應用,若結合“例1”來看,似乎是“交通工具剎車類問題”.但由于傳送帶不是靜止而是速度反向且大于物體初速度,故物體先做勻減速直線運動,后返回做勻加速直線運動(若傳送帶足夠長),且加速度不變,即遵循勻變速直線運動.
取向右為正方
其中
v0=20m/s,a=μg=-8m/s2,
則
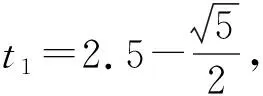
舍解的依據:表面看兩解都大于0,沒有出現“例2”中的“時間方向”性的問題,也沒有出現“例1”中“交通工具剎車”情況而停止.但沒有考慮“傳送帶長度”的“潛在約束”.通過判斷發現,物體向右前進25m時速度為0,已超出傳送帶長度而“離開”傳送帶.故t2不符合實際情況.
被舍解的意義:在分析中沒有注意到“傳送帶”實際長度的“約束性”,t2解實際是反應傳送帶足夠長的情況下,物體再此返回到20m位置時的情型.
4 能效的合理性
物理模型的建立首先符合數學規律,但符合數學規律的不一定有物理意義,或者即便有物理意義,但“性價比”(效率等)較低.理論上可以存在,但不利于采用,此時的“解”要舍去.
例4.如圖2所示,一電動機用電動勢為100V的電源供電,電源內阻為r=1Ω,電動機的線圈內阻為R=4Ω,正常工作時電機輸出機械功率為180W.試確定此時電路中電流是多少?
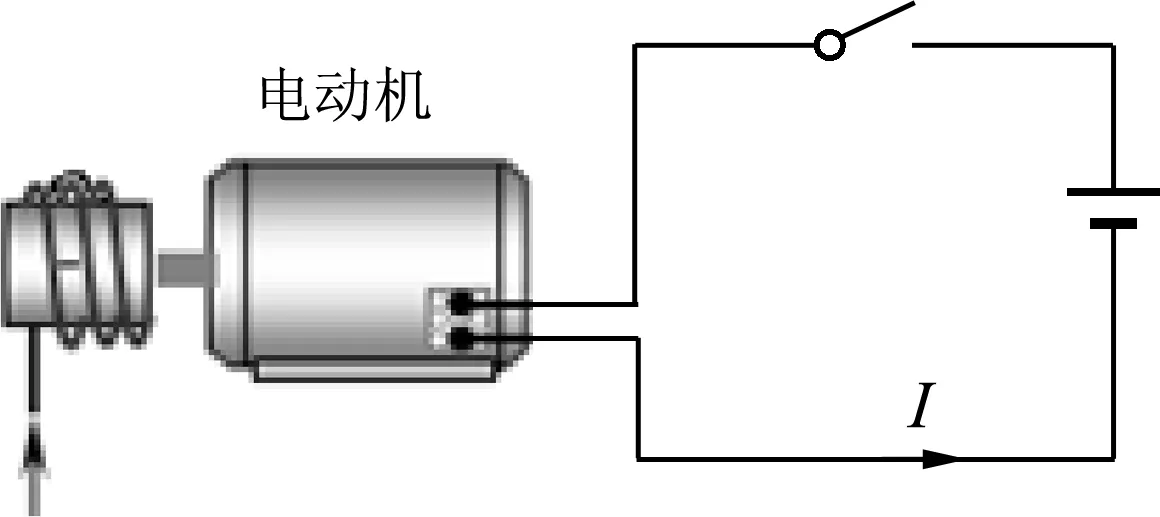
圖2
解析:本題只是閉合電路歐姆定律的應用問題,由題意不難得到如下關系.
P機=EI-I2(R+r),
即180=100I-I2(1+4),
有I1=2A或I2=18A(舍去).
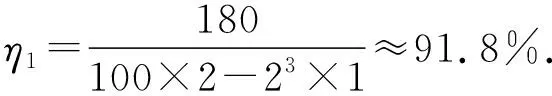
被舍解的意義:I2=18A時,在數學上是有意義的.理論上符合這種數學解的電機是都可以生產出來的,只是兩種(2A與18A)電機制造工藝有所區別.這與電機工作原理(線圈的電感等)有關,電機工作時內部線圈產生反電動勢直接影響電機的工作效率.因此實際生產的電機是要保證其工作效率的.
5 “淺顯”的不可能
有些物理過程的結論本身就具有不確定性,然而不確定中有隱性而“淺顯”(理所當然)的約束.比如:如果要求一個物體同要追上另一個物體,這就必然要求后面物體的速度大于前面物體的速度(這個約束關系是“淺顯”的).

圖3
例5.如圖3所示,在水平面上兩個小球A、B質量為m1=2kg,m2=1kg.B靜止,A以速度2m/s向右與B發生彈性碰撞.則碰撞后兩小球的速度分別是多少?
解析:“碰撞”是關于“動量守恒”應用的實際模型(內力遠大于外力).由于發生彈性碰撞,又滿足機械能守恒,故有
m1v1=m1v1′+m2v2′,
聯立方程代數求解得
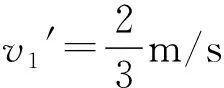
v1′=2m/s和v2′=0(舍去).
舍解的依據:由于碰撞過程中產生的相互作用力是排斥力,即碰撞后B物體一定向右運動且以后不會再發性相互作用了,故不可能出現v2′=0的情況.
被舍解的意義:從數學上看,只是滿足兩個方程即可,被舍的解實際上是初狀態速度情況.
延伸歸納:關于同向追及碰撞情形可能性系列問題中,存在以下“淺顯”的不可能情況: (1) 碰撞前后都速度大于前者速度; (2) 碰撞后前者速度小于等于后者速度; (3) 碰撞中機械能不可能增加,也不可能比“完全非彈性碰撞”情況下損失的機械能更多.
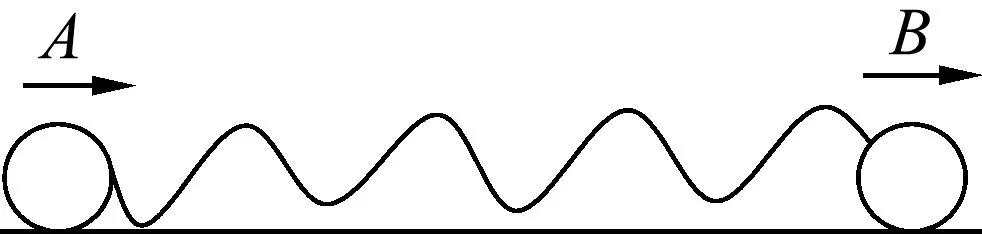
圖4
進階:如圖4所示,一根不可伸長的細繩連接A、B兩個小球,置于光滑水平面上,mA=2kg,mB=1kg,現給A和B小球提供瞬間初速度,速度分別為vA=2m/s向左,vB=3m/s向右,細繩繃斷過程中機械能損失50%.求:細繩繃斷后兩球的速度.
解析:本題依然是考查動量與機械能的綜合問題,建立動量關系與機械能關系即可.
mAvA+mBvB=mAvA′+mBvB′,
取向左為正方向,解得
vA′=1.5m/s,vB′=-2m/s;
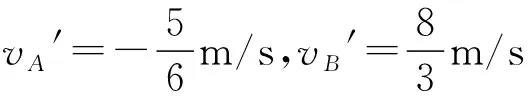

圖5
舍解的依據:兩小球在背向運動過程導致細繩繃斷,細繩繃斷一定發生在小球相對遠離過程中,因此細繩斷后兩小球的速度一定是相對遠離.而第二解A向右,B向左,即相互靠近,不具實際物理意義.
被舍解的意義:由題設模型可以聯立解析中的方程組,但是根據這個方程組無法判斷兩小球之間的作用方式,而正是由于“繃緊至斷”的這種方式使“第二解”舍去.如圖5所示,若A球在右,B球在左.其他條件相同而發生相互碰撞.求兩球碰后的速度.這個“碰撞”模型與“繃斷”模型的數學模型是一樣的,在“碰撞”模型中“第二解”就具體實際物理意義,但“第一解”又要“舍去”(碰撞之后相互遠離).
數學是表達物理的一種語言,很多物理理論都是用數學方法進行分析、推理與總結.然而利用數學手段的解決的問題需要結合實際情景,經得起實踐的檢驗,排除沒有實際物理意義的解,才能坐實“結論”的科學性,也確定了“論證”的重要性.
參考文獻:
1 張健敏.注重對物理題多值的討論[J].物理教師,2000(12):45-46.
2 周偉玲.例談對物理問題中數學解的理解與取舍[J].物理實驗(中學部分),2004(2):10-11.

