三相永磁同步電機的無差拍直接轉矩容錯控制
劉加妮,李益華,陳長凱,陳 龍,葉詩婷
(1.長沙理工大學電氣與信息工程學院,湖南長沙410114;2.湖南中新工程項目管理有限公司,長沙410000)
1 引言
電機的容錯性是在汽車和航空等領域中的一個關鍵性能指標,提高電機的容錯性可以提高系統的安全可靠性。目前電動機驅動系統的可靠性方案主要有兩種:余度方案以及容錯方案[1]。余度方案采用冗余思想,通過重復配置系統資源來滿足系統高可靠性的要求,但系統利用率不高;容錯方案主要從容錯式電機本體[2-7]、驅動拓撲[8]以及容錯控制算法[9-16]三個方面出發,切除故障相,保證系統在不對稱狀態下繼續正常工作,因此大大提高了系統的利用率,但是對控制水平也大幅度提高,要求控制技術有非對稱控制能力。
目前,國內外研究主要集中于大于三相的多相永磁容錯電機及其容錯控制算法,且對TP-PMSM的容錯控制僅局限于驅動拓撲,例如三相四橋臂[17]和三相四開關容錯控制[18]。多相容錯電機本身具有較強容錯能力再結合高性能的容錯控制算法,整個系統具有強容錯能力,提高了系統的可靠性和安全性。然而TP-PMSM本體不具備容錯能力,雖驅動拓撲容錯控制能保證電機故障后仍然運行,但不能獲得滿意的運行性能[17-18],因此,需進一步研究其容錯控制算法,提高系統的動靜態性能和容錯性。
本文旨在盡可能少地修改控制結構并減少由于容錯能力而增加的額外計算負擔,研究TP-PMSM的容錯控制算法。直接轉矩控制具有“天然的”容錯性,并且已經成功應用于多相永磁容錯電機[16]。傳統PMSM直接轉矩控制存在的磁鏈、轉矩脈動大、開關頻率不固定等問題,而結合無差拍控制形成的無差拍直接轉矩控制(DB-DTC),不僅動態響應快,而且定子磁鏈和轉矩的脈動小,具有良好的動靜態性能[19]。因此,為了提高TP-PMSM的容錯運行性能,本文結合其故障模型和DB-DTC,提出了無差拍直接轉矩容錯控制(DB-DTFTC),使電機在故障前后都能獲得滿意的動靜態運行性能。
2 TP-PMSM驅動電路的容錯拓撲結構
在TP-PMSM控制系統中,若其中某相發生故障,可以通過隔離故障元件,斷開該相,并將電機定子繞組中性點與逆變器母線的或附加的逆變器支路的中性點連接起來,通過調整剩余兩相電流大小與相位,從而保證電機故障前后旋轉磁動勢保持恒定,進而使得電機正常運行[20]。
如TP-PMSM繞組以星型連接無中線,若A相發生故障被斷開,則剩余兩相將形成串聯單相電機,此時電機的合成磁動勢為:


圖1 TP-PMSM驅動電路的容錯拓撲硬件配置

如圖1所示,在TP-PMSM的控制系統中,根據系統故障的情況,由軟件發出命令,進行系統的重構,隔開故障元件和斷開故障相A,并將電機定子繞組中性點與逆變器母線的或附加的逆變器支路的中性點連接起來,且對剩余兩相電流的相位和幅值做一些合理的調整,即可以使電機正常運行。




3 TP-PMSM的容錯數學模型
3.1 TP-PMSM在三相靜止坐標系的容錯數學模型
假設A相發生故障被斷開,那么定子側的電壓方程為:

或寫成矩陣形式:

磁鏈方程為:


其中,UB,UC,iB,iC,φB,φC分別為 B、C 相的相電壓、相電流和磁鏈;Rs是定子繞組電阻矩陣;Lss和Lms為定子繞組電感矩陣,而Mψr為折算到定子測的轉子磁鏈幅值;θre為轉子位置,P為極對數。
轉矩方程為:

由式(7)可知,電磁轉矩Te由電動機的基本電磁轉矩和電動機d、q磁路不對稱而產生的磁阻轉矩兩部分組成。
3.2 TP-PMSM在兩相旋轉坐標系的容錯數學模型
利用變換矩陣[12]

可將TP-PMSM在三相靜止坐標系的電壓、磁鏈和轉矩方程(4)-(7)轉換到與轉子磁通定向的兩 相旋轉坐標系dq。因此可得,TP-PMSM在A相故障情況下,以轉子磁鏈定向的兩相旋轉坐標系dq中的電壓、磁鏈和轉矩方程:電壓方程:

磁鏈方程:

轉矩方程:

式中ωrm是轉子角速度。由式(10)可知,TP-PMSM經變換矩陣得到兩項旋轉坐標系的電磁轉矩就與正常運行時的電磁轉矩方程相等。
由此可見,故障時TP-PMSM在兩相旋轉坐標系dq的電阻矩陣和電感矩陣比正常運行時的電阻矩陣和電感矩陣更加復雜。故障時的電阻矩陣和電感矩陣不僅包括常數項,而且還存在dq軸之間的正弦交叉耦合項。該正弦交叉耦合項與轉子位置 θre相關[21]。
4 無差拍直接轉矩容錯控制策略
在TP-PMSM正常運行時,無差拍直接轉矩控制利用TP-PMSM的離散狀態方程,以電磁轉矩和定子磁鏈幅值零誤差為控制目標,直接計算出應施加在定子端的電壓矢量,最后經空間矢量調制技術(Space Vector Module—SVM策略)得到開關信號,實現了電機的有效控制。其中,轉矩和磁鏈控制環無需PI調節器,結構簡單,開關頻率恒定。DB-DTC不僅繼承了傳統DTC動態響應快的優點,而且極大程度上削弱定子磁鏈和轉矩的脈動,具有良好的動靜態性能。同時采用定子電流觀測器預測下一周期的定子電流,消除控制系統時間周期上的誤差,實現系統實時、精確地控制[19]。因此,在TP-PMSM故障運行時,即使電機僅有兩相電流,無差拍直接轉矩容錯控制算法/能夠產生合適的定子端的電壓矢量。這個矢量是表示每一開關周期定子磁鏈的變化,應該能夠在TPPMSM產生旋轉磁場,以滿足期望的氣隙轉矩和定子磁鏈。
4.1 轉矩線性方程
如TP-PMSM故障運行時的兩相旋轉容錯模型式(8)-(10)所示,因為電機繞組電阻矩陣和電感矩陣存在RsE和LlsE,所以電機轉矩線性方程、定子磁鏈和電流觀測器也變得更復雜,且顯著增加控制單元計算負擔。

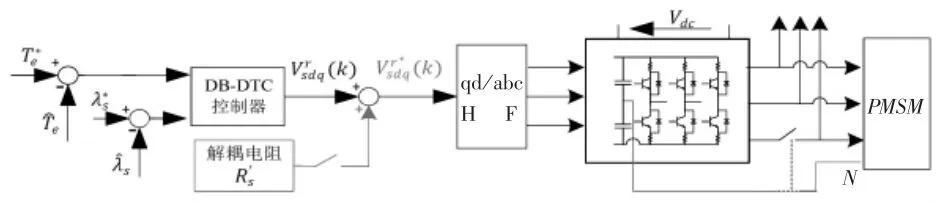
圖2 驅動電路容錯拓撲硬件配置和投入補償電阻示意圖

在無差拍直接轉矩容錯控制系統中,電機的期望電壓指令對應無差拍控制器的輸出加附加電壓降△V。無差拍控制器輸出是由TP-PMSM的容錯模型中轉矩方程(10)求導離散化確定的。先對式(10)求一次導:
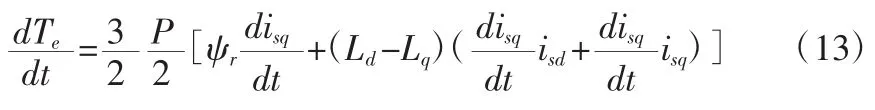
假設樣本時間為Ts,將式(13)離散化:

將TP-PMSM的容錯模型中電壓方程(8)和磁鏈方程(9)聯立,整理和離散化后,將式(14)代入便可以得出電機故障運行時的轉矩線性方程(15):
由式(15)可發現,該轉矩線性方程與TP-PMSM正常運行時的轉矩線性方程式是一樣的。

同時電機定子磁鏈幅值滿足:



然而,考慮功率轉換器的直流母線電壓給定的實際極限,只有一個Usd(k)值是可行的。將Usd(k)代入式(15)便可得到Usq(k)。
4.2 定子磁鏈觀測器和電流觀測器
與正常運行時一樣,TP-PMSM故障運行時的定子磁鏈和電流可以用離散觀測器估計,并且定子磁鏈和電流觀測器故障前后不需做任何改變。定子磁鏈觀測器采用加權系數的方式結合定子磁鏈觀測器采用加權系數的方式結合“電流模型”和“電壓模型”來估計定子磁鏈。因此,定子磁鏈觀測器在低轉速和高轉速下都可以獲得足夠精確的定子磁鏈估計值。假設Lls=0,RsE通過式(11)完全解耦,利用式(8)和式(9)可設計閉環觀測器。圖4給出了所使用的離散定子磁鏈觀測器。因為對R's產生的電壓降進行了補償,所以正常運行時的定子磁鏈觀測器數學模型也是適用的。
如圖(3)所示,采用帶有電壓補償的定子電流觀測器可以獲得零相位滯后磁鏈估計。它采用Luenberger觀測器,能夠根據采樣電壓和電流立刻估計在下一個采樣周期的電流[22]。

圖3 定子磁鏈觀測器和電流觀測器

圖4 無差拍直接轉矩容錯控制框圖
如圖(4)所示,是 TP-PMSM 的 DB-DTFTC 框圖。如圖可知,電機的控制結構故障前后大體一致,使用相同的控制律和觀測器。只是故障情況下,坐標轉換矩陣不同和為了解耦R's引起的電壓降進行了電壓補償。坐標變換矩陣集可以根據系統的狀態選擇:正常運行(H)和故障運行(F)。
5 無差拍直接轉矩容錯控制仿真
為了驗證TP-PMSMDB-DTFTC的控制性能,在MATLAB/Simulink分別進行了TP-PMSM正常運行的無差拍直接轉矩控制、A相斷開帶解耦的無差拍直接轉矩容錯控制和A相斷開不帶解耦的無差拍直接轉矩容錯控制,并對三種情形下的運行性能進行對比。試驗中TP-PMSM參數見表1。

表1 TP-PMSM參數
仿真實驗中,令負載轉矩恒等于4Nm,轉速為50rad/s(高速),在 0.5s轉速變為 10rad/s(低速),在 1s轉速又變回50rad/s。正常運行下的轉子角速度ωrm、氣隙轉矩Te和定子相電流如圖 5(a)。圖 5(b)和圖 5(c)分別給出了 A 相開路故障時帶解耦和不帶解耦的轉子角速度ωrm、氣隙轉矩Te和定子相電流Iabc。在這三種情況下,電機速度都是可控的,且運動控制器的帶寬為10Hz,定子電流觀測器帶寬為40Hz,磁鏈觀測器帶寬為10Hz。

圖5 電機轉子角速度ωrm、氣隙轉矩Te和定子相電流Iabc
從圖 5(a)與圖 5(b)可以看出,采用帶解耦 DB-DCFTT的TP-PMSM在A相斷開后,轉速和轉矩的運行性能與正常運行時相似,并且剩余兩相電流幅值增加。此外,從圖5(b)和圖5(c)可以看出,采用不帶解耦 DB-DTFTC 的 TPPMSM的轉速和轉矩在低速時有一定的紋波出現,電流不變,但電機仍然可以安全運行。
6 結論
本文在三相永磁同步電機(TP-PMSM)容錯拓撲和斷相故障模型基礎上,結合無差拍直接轉矩控制(DTC),提出了TP-PMSM無差拍直接轉矩容錯控制策略(DB-DTFTC)。該控制策略可使TP-PMSM發生故障后,在剩余兩相電流下運行,并保持與正常運行時相同的動靜態性能。
仿真結果表明,采用DB-DTFTC TP-PMSM即使在故障時,不僅動態響應快,而且極大程度地削弱了定子磁鏈和轉矩的脈動,電流觀測器能預測定子電流,大大提高了控制精度。因此,采用DB-DTFTC大大提高了TP-PMSM的運行可靠性和安全性。

