某型發動機亞熱帶島礁氣候下的可靠性分析與保障

李本威，楊欣毅，韋 祥

（海軍航空大學航空基礎學院，山東煙臺264001）

0 引言

某型發動機是海軍航空兵某戰斗機的重要裝備，長期在亞熱帶高溫、高濕、高鹽的惡劣使用環境下使用，發動機使用可靠性承受著較大的考驗[1-3]。為確保飛機具備完好的出勤能力，發動機備件的供應保障顯得十分緊迫和重要[4-7]。

本文結合多年的發動機故障統計情況，分析其亞熱帶氣候條件下的可靠性，提出保障率概念，運用粒子群優化[8-12]求解方法，研究發動機在不同的駐島礁期間的備件供應保障問題，給出基地級保障和不同駐島時間內發動機備件攜行保障策略。

1 發動機使用可靠性分析

發動機使用可用度（完好率）取決于發動機的固有可用度、維修能力和備件保障能力[13-14]。發動機固有可用度的計算式為

式中：TBF=K2·Ke·TFBF，為平均故障間隔時間，TFBF為平均故障間隔飛行小時；K2為運行比（總工作時間與飛行時間的比值），參考某型發動機近幾年的空地使用時間統計情況，發動機地面時間占比約為20%， 取1.2；Ke為環境因子，表明使用環境對發動機可靠性的影響程度；TCM為平均修復時間（不包括預防性維修、管理和保障延遲時間）。

環境因子Ke可利用某型飛機設計定型的溫和地域可靠性數據和亞熱帶地域使用的可靠性數據進行估計。某型飛機設計定型時平均故障間隔3.02 h，外場級平均修復時間為1.06 h，固有可用度評估為0.75（75%）。該型飛機裝備部隊多年，部隊機務維護人員對其維護的熟練程度已與設計定型時工業部門的維護人員相當。近幾年某型系列飛機的質量及維修情況統計見表1。

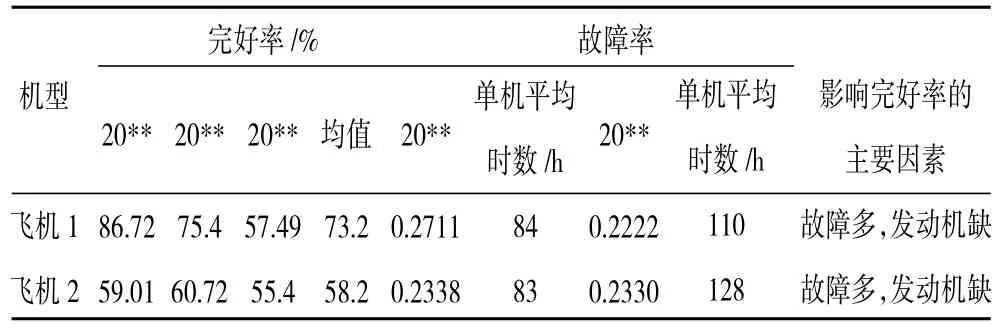
表1 某型系列飛機質量及維修情況統計

從表中可見，某型飛機的使用完好率（使用可用度）低于設計定型時的可用度，其主要原因是在亞熱帶潮濕、炎熱的氣候條件下長期使用的環境對其可靠性造成了影響。根據以上考慮，計算得到某型系列機在亞熱帶使用的平均故障間隔時間為2.9 h，平均故障間隔4.05 h。可以估算出，亞熱帶氣候相對內陸溫和地域氣候而言，對飛機產品應力壽命的環境影響因子Ke=0.8。

統計發動機近5年的使用數據，外場暴露各類有效技術質量問題140項、1350起。根據式（1）統計分析得到的發動機平均故障間隔時間（Mean Time Between Failure，MTBF，TMBF）和空中停車（in-flight shut down，IFSD）可靠性指標見表2。

表2 發動機MTBF和IFSD隨工作時間變化情況

從表中可見，某型發動機的MTBF指標呈不斷增長趨勢，但與設計成熟期可靠性指標（MTBF）不小于150 h、空中停車率不大于0.1次/1000飛行小時、發動機提前換發率不大于0.5次/1000飛行小時的要求還存在一定差距。

在統計的發動機各類技術質量問題當中，主機故障主要集中體現在振動超標、進氣機匣殼體裂紋、整流板裂紋和尾噴管作動筒漏油等方面；傳動潤滑系統故障集中體現在滑油金屬含量超標、磁力密封裝置和皮碗漏油、滑油泵組調壓活門卡滯等方面；控制系統故障集中體現在燃油增壓泵漏油和傳感器虛警等方面。為此，在短期內不能有效提高發動機或某些部附件固有設計可靠性的前提下，要確保飛機出勤率和發動機使用可用度（完好率），只能重點關注發動機主機和上述重點成品件的備件供應保障問題。

2 基于保障率的發動機供應保障模型建立與求解

某型發動機除主機外，還有47種成品件。為建立基于保障率的發動機供應保障模型，作如下假設：（1）最大程度確保飛機出勤率，不考慮飛機間的發動機串換件；（2）在島礁基層級所有故障件只更換備件，不實施修理；（3）發動機備件缺貨將使發動機不完好；（4）各發動機部件的故障與備件缺貨的過程相互獨立；（5）發動機的完好率與備件的儲備量及儲備策略相關；（6）故障的出現是隨機的，暫不考慮發動機備件供應等待時間。

基于保障率的發動機供應保障模型是以飛機機群的發動機完好率為目標函數，以備件購置費用限制為約束條件，即：在備件購置費用約束條件下，尋求基地級最優備件庫存或島礁基層級最優攜行保障策略，使得在此策略下機群保障的發動機完好率達到最大。供應保障模型的數學描述如下：

目標函數為

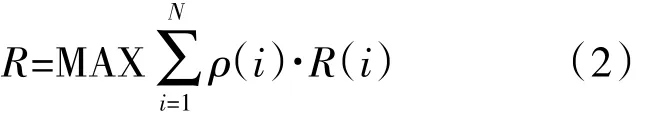
式中：R為機群的發動機完好保障率；ρ（i）為第i個器材備件的權重系數；R（i）為第i個器材備件的保障率。

約束函數為

式中：C（0）為發動機備件購置總經費；C（i）為第i個備件的單價；X（i）為第i個備件的數量。

保障率定義為

式中：N（i）為部件的裝機數；λ（i）為第i個備件的故障率；Tk（i）為部件的裝機工作時間；X（i）為器材備件需求量。

海軍發動機維修保障采用2級體制，即基層級保障和基地級保障。按照2級保障結構，模型中航空發動機備件保障配置表示為

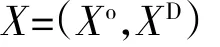
式中分別為基層級和基地級的島礁攜行和庫存配置；L為備件種類數；Xl為第l種備件的數量。假設C=（c1，c2，…，cl），cl為第l種備件的單價，2級供應保障模型為

備件權重ρ（i）是1種新的衡量部件在發動機中作用大小的概念，從備件配裝發動機的重要性、可維修能力、故障程度3個方面衡量。在備件配裝發動機的重要性方面，每個備件在發動機上的作用程度不同，有些是發動機的關鍵部件，屬于壽命件，影響飛行安全；有些是發動機的重要部件，屬于視情監控部件，影響飛行任務的執行；有些屬于一般部件，不影響安全飛行和任務的執行。從備件配裝發動機的重要性來看，在2級維修供應保障體制中，基地級庫存保障不僅要考慮此類備件的故障更換，而且應考慮到壽更換。從可維修能力角度來看，把發動機備件分為可修件與不可修件，由于可修件修復后可以重新裝機使用，相當于1個新的備件，在備件優化中起到重要作用。在2級維修供應保障體制中，根據前面的假設，基地級庫存保障可以認為可修復備件具有修復能力；駐島礁基層級備件發生故障主要以更換為主，認為不具有修復能力。故障程度是根據部件在使用過程中發生故障的統計情況確定的，同時依據統計情況對部件的故障程度進行等級劃分。故障程度高的部件，備件保障中關注權值系數會更大。故障程度的評估具有時間效應。

對機群進行完好發動機備件保障率優化，關鍵是在滿足約束條件（購置總經費不超過C（0）的前提下）確定各備件需求量的最優組合{X（1），X（2），…，X（N）}opt，從本質上看屬于離散優化問題，是1個典型的N-P問題。采用粒子群優化算法（QPSO）對機群的完好保障率進行優化求解[15]。

粒子位置更新方程為

粒子的狀態用位置向量來描述。控制參數為收擴系數α。

利用量子粒子群進行機群完好保障率優化的核心是，每個粒子即為各備件數量的組合{X（1），X（2），…，X（N）}opt，由于約束條件是不等式，并且是購置總經費不超限，因此在迭代求解過程中增加判斷條件，刪除種群中不滿足約束條件的粒子，并引入變異機制，對其他粒子進行變異處理，補充相同數量的粒子，以維持種群的規模不變，同時也有利于增加粒子的多樣性，提高算法的搜索效率。

（1）初始化。根據指定數目生成初始種群p={X（1），X（2），…，X（num）}opt，其中每個粒子X（i）表示 1種可能的備件數量組合。

（2）判斷所有粒子是否滿足約束條件，不滿足則刪除，并變異生成相同數目的替代粒子。

（3）按照機群的完好保障率計算粒子的適應度。

（4）計算種群中粒子的個體極值和全局極值。

（5）按照式（6）對粒子進行位置更新。

（6）判斷算法是否達到最大迭代次數，若是則程序運行結束，并輸出相應結果，否則轉至步驟（2）。

3 發動機備件供應保障優化策略

據前面分析，2級備件保障模式下的備件權重系數ρ（i）的取值不同。假定重要性、可維修能力、故障程度3個方面的權值分配見表3。發動機每個可更換部件的故障程度，按照統計周期內在用發動機的該成品件裝機數量與該故障件數量之比來估計，可分為高故障率、一般故障率、低故障率3個層次。故障率大于0.1為高故障率；故障率處于0.03~0.1之間為一般故障率；故障率小于0.03為低故障率。

每個部件的重要性、可維修能力、故障程度是不同的，按照3項的權值分配再求和，得出該部件的累計權重分數q（i）；然后對艦載機所有成品件的權重分數進行求和，得出1個總權重分數則該部件的權重系數為

【點評】小作者選取自己的兩件閱讀趣事加以敘述，讓我們看到一個戴眼鏡的小書迷的形象。習作敘事清楚、流暢自然。

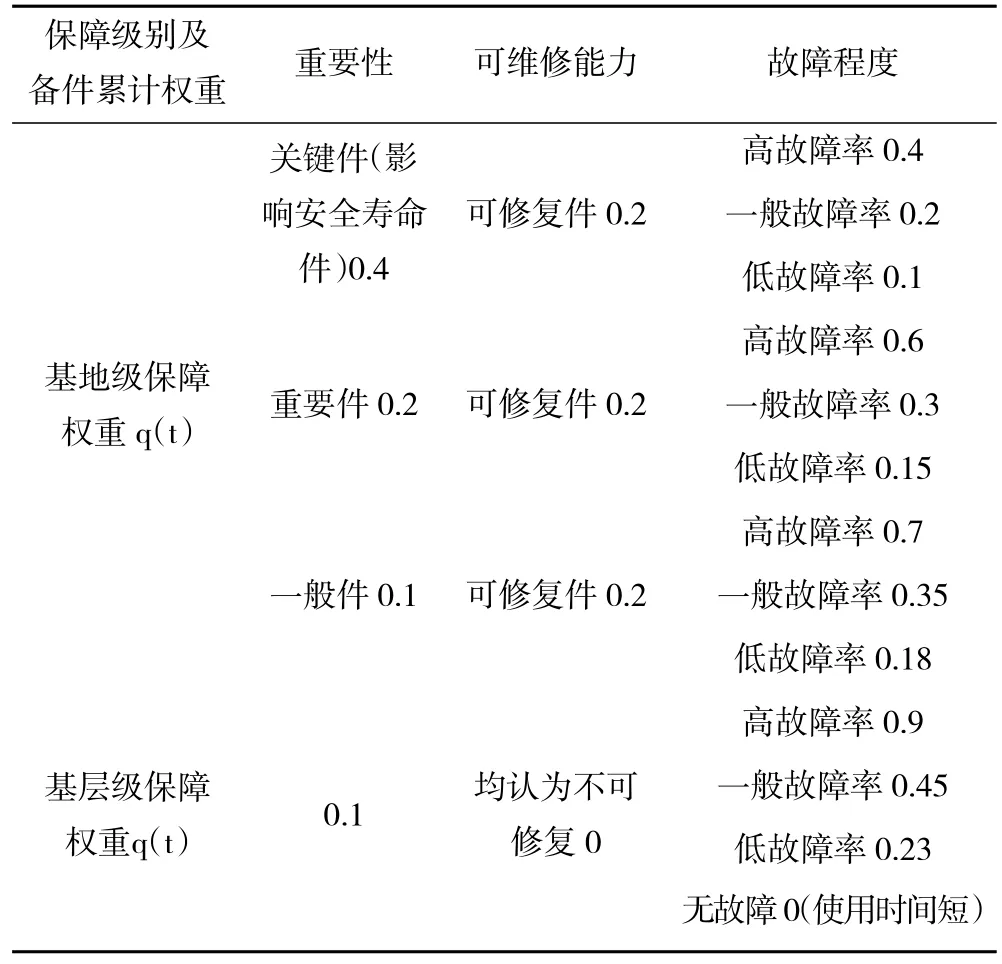
表3 航材備件重要性、可維修能力、故障程度的權值分配

根據第2章的航空器材優化保障模型建立方法，統計105臺發動機故障信息，給定某型發動機基本信息，見表4。

表4 某型發動機及成品件基本信息

依據某型發動機及成品件基本信息表，按照2級保障體制構建的發動機及成品件權值系數見表5、6。

某型發動機的可靠性分析按表5中的48個發動機主機及成品件組成串聯系統進行，發動機整機故障率和各成品件故障率的關系可表示為

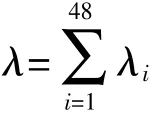
式中：λi為發動機主機及成品件的故障率。

利用量子粒子群優化算法對發動機及成品件基地級庫存保障數量或駐島礁攜行數量進行優化分析計算。迭代次數設為50，種群數量為100，其中每個粒子X={x1，x2，…，xm}的第i個維度xi表示第i個成品件的配置數量。粒子的每個維度下限設置為0（即成品件數量可以為0），而粒子的每個維度的上限依據每個成品件的平均無故障工作時間、成品件總工作時間設置，其關系式為

表5 基地級發動機及成品件庫存保障的各種權系數

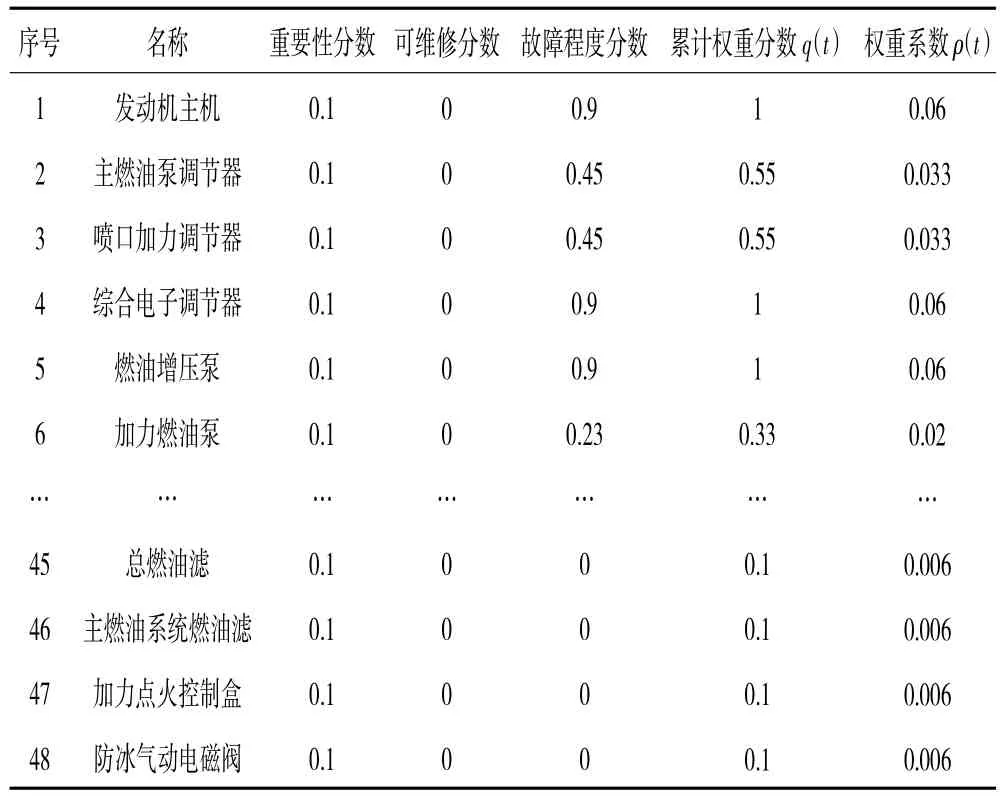
表6 基層級發動機及成品件庫存保障的各種權系數

式中：α為余度系數，取值為1~1.5。

在迭代過程設置判斷條件，當粒子對應的總價格超過允許范圍則進行調整，使其重新滿足限制條件。

最優粒子對應的目標函數隨迭代次數變化曲線如圖1所示。從圖中可見，隨著種群的進化，最優解對應的目標函數值被不斷提高，最終目標函數值達到47.9，而最優解的備件采購總價格是約束價格的93.5%，沒有超過約束條件，如圖2所示。

圖1 最優解的迭代進化過程

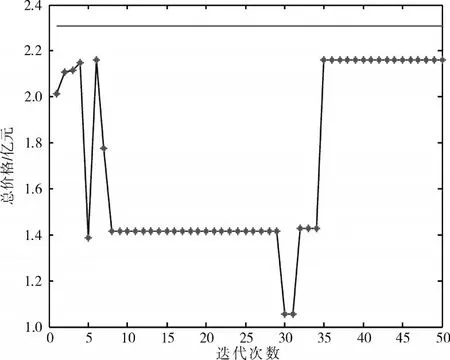
圖2 最優解的總價格變化過程

通過最優解的求解得到的發動機壽命期內基地級庫存保障策略見表7。

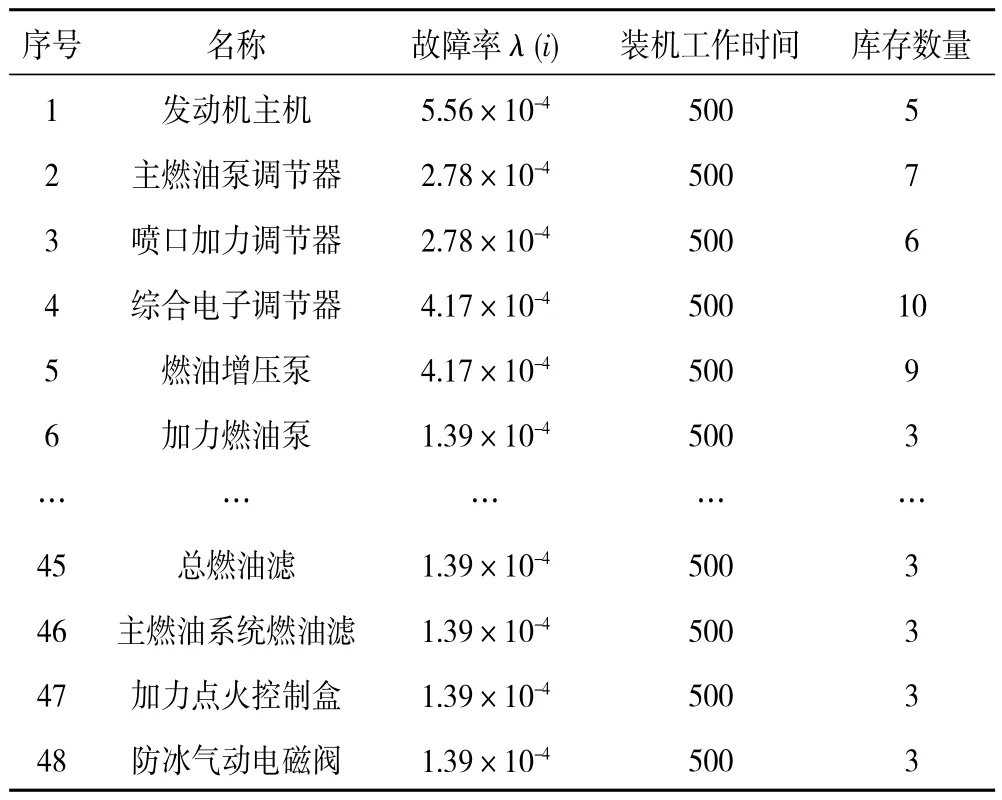
表7 基地級發動機及成品件庫存保障數量

按照同樣方法分別計算24架機駐島礁3、6個月期間發動機備件的攜行保障策略，見表8。求解過程對應的最優解的迭代過程曲線分別如圖3、4所示。圖3、4分別表示3、6個月駐島事件優化計算過程，種群最優解對應的目標函數（即保障率）隨迭代次數的增加均能有效地提高。

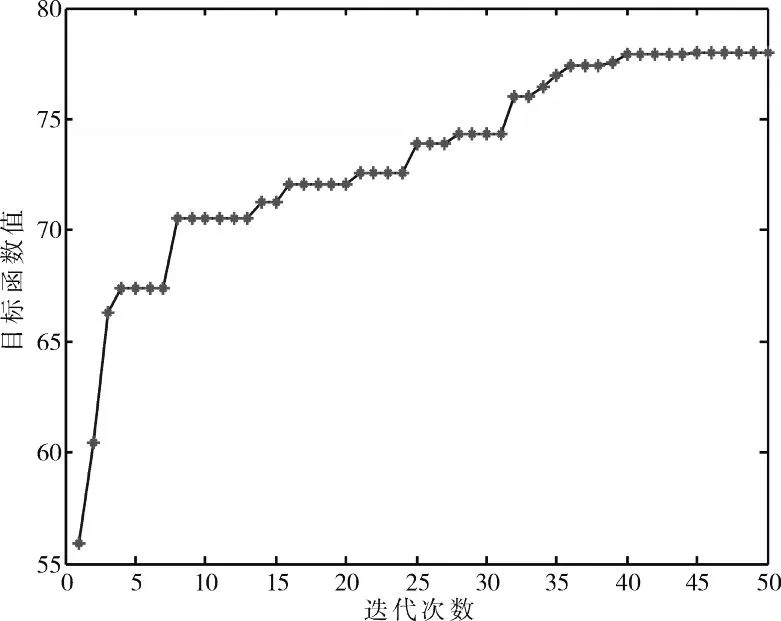
圖3 3個月駐島迭代進化過程

圖4 6個月駐島迭代進化過程

表8 駐島期間發動機及成品件攜行保障策略

4 結論

（1）引入環境因子，利用大量發動機使用數據，對亞熱帶氣候條件下某型發動機可靠性進行評估。隨著發動機及附件產品質量的不斷改進，發動機可靠性指標MTBF可達到104.4，但與成熟期的目標仍有較大差距。在近期駐島礁時間內，要確保發動機使用可用度（完好率），仍需重點關注發動機主機和成品件的供應保障問題。

（2）以飛機機群的發動機完好率為目標函數，以備件購置費用限制為約束條件，建立基于保障率的發動機供應保障模型。重點關注發動機備件重要性、可維修能力、故障程度等因素，基于先進的量子粒子群尋優求解方法，給出基地級庫存和駐島礁基層級的發動機備件供應策略。

[1]孔瑞蓮.航空發動機可靠性工程[M].北京：航空工業出版社,1996：4-5.KONG Ruilian.Aeroengine reliability engineering[M].Beijing:Aviation industry Press,1996.（in Chinese）

[2]王大偉,馬艷紅,洪杰.基于危害度航空發動機可靠性評估模型及應用[J].北京航空航天大學學報,2008,34（8）:883-886.WANG Dawei,MA Yanhong,HONG Jie.Reliability assessment model and application for aeroengine based on criticality method[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34（8）:883-886.（in Chinese）

[3]任淑紅.民航發動機性能可靠性評估與在翼壽命預測方法研究[D].南京：南京航空航天大學,2010.REN Shuhong.Research on methods of performance reliability assessments and life on wing prediction for civil aeroengine[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010.（in Chinese）

[4]孫闖,何正嘉,張周鎖,等.基于狀態信息的航空發動機運行可靠性評估[J].機械工程學報,2013,49（6）:30-37.SUN Chuang,HE Zhengjia,ZHANG Zhousuo,et al.Operating reliability assessment for aeroengine based on condition monitoring information[J].Journal of Mechanical Engineering,2013,49（6）:30-37.（in Chinese）

[5]郭波,陳童,黃卓,等.航空發動機組合維修策略的備件需求規律[J].系統工程理論與實踐,2010,30（5）:769-777.GUO Bo,CHEN Tong,HUNAG Zhuo,et al.Spare parts demand law of aviation engine with combination maintenance policy[J].System Engineering Theory and Practice,2010,30（5）:769-777.（in Chinese）

[6]白芳，左洪福，任淑紅，等.航空發動機拆換率平滑方法[J].航空動力學報,2008,23（10）:1821-1828.BAI Fang,ZUO Hongfu,REN Shuhong,et al.Research on smoothing method for engine removal rate[J].Journal of Aerospace Power,2008,23（10）:1821-1828.（in Chinese）

[7]白芳，左洪福.基于調度計劃的航空發動機備份數量決策方法研究[J].機械科學與技術,2009,28（1）:92-97.BAI Fang,ZUO Hongfu.A decision method for the quantity of spare aero-engines based on scheduling[J].Mechanical Scinece and Technology for Aerospace Engineering,2008,23（10）:1821-1828.（in Chinese）

[8]方偉,孫俊,謝振平,等.量子粒子群優化算法的收斂性分析及控制參數研究[J].物理學報,2010,59（6）:3686-3694.FANG Wei,SUN Jun,XIE Zhenping,et al.Convergence analysis of quantum-behaved particle swarm optimization algorithm and study on its control parameter[J].Acta Physica Sinica,2010,59（6）:3686-3694.（in Chinese）

[9]彭鵬菲,于錢,李啟元.基于優先排序與粒子群優化的裝備保障任務規劃方法[J].兵工學報,2016,37（6）:1082-1088.PENG Pengfei,YU Qian,LI Qiyuan.A planning method of equipment support task based on priority ordering and particle swarm optimization algorithm[J].Acta Armamentarii,2016,37（6）:1082-1088.（in Chinese）

[10]彭鵬菲,于錢,李啟元.基于改進粒子群優化的多目標裝備保障任務規劃方法[J].系統工程與電子技術,2017,39（3）:562-568.PENG Pengfei,YU Qian,LI Qiyuan.Method of multiobject equipment support task planning based on improved particle swarm optimization[J].System Engineering and Electronics,2017,39（3）:562-568.（in Chinese）

[11]張凱,趙國榮,姜靜.粒子群算法在武器裝備保障資源優化中的應用[J].兵工自動化,2010,29（1）:1720-1723.ZHANG Kai,ZHAO Guorong,JIANG Jing.Application of PSO in weapon equipment safeguard resource optimization[J].Ordnance Industry Automation,2010,29（1）:1720-1723.（in Chinese）

[12]倪現存,左洪福,劉明,等.基于免疫粒子群算法的民機備件庫存配置優化方法研究 [J].機械科學與技術,2008,27（12）:1660-1667.NI Xiancun,ZUO Hongfu,LIU Ming,et al.A method for civil aircraft spare parts inventory allocation based on particle swarm optimization with immunity algorithms[J].Mechanical scinece and technology for Aerospace Engineering,2008,27（12）:1660-1667.（in Chinese）

[13]宋兆泓.航空發動機可靠性與故障抑制工程 [M].北京:北京航空航天大學出版社,2002：2-5.SONG Zhaohong.Aeroengine reliability and fault suppression engineering[M].Beijing:Beijing University of Aeronautics and Astronautics Ppress,2002.（in Chinese）

[14]陳卓,薛慶增,李冬,等.航空發動機使用可靠性研究[J].航空發動機,2010,36（3）:10-15.CHEN Zhuo,XUE Qingzeng,LI Dong,et al.Service reliability study on Aeroengine[J].Aeroengine,2010,36（3）:10-15.（in Chinese）

[15]方偉,孫俊,須文波.基于微分進化算子的量子粒子群優化算法及應用[J].系統仿真學報,2008（24）:6740-6744.FANG Wei,SUN Jun,XU Wenbo.Improved quantum-behaved particle swarm optimization algorithm based on differential evolution operator and its application[J].Journal of System Simulation,2008（24）:6740-6744.（in Chinese）