尖頭彈侵徹金屬板花瓣型破口成形過程仿真分析

伍星星，劉建湖，張倫平，孟利平，汪俊

中國船舶科學研究中心，江蘇無錫214082

0 引 言

花瓣型破口是金屬板在強沖擊載荷作用下的典型破壞模式之一，迄今為止，國內外已對該破壞模式展開了較多研究。在實驗方面，Nurick和Radford［1］對不同藥量接觸爆炸下的薄板進行了一系列實驗，逐步從薄板的凹陷、沖塞毀傷模式觀察到了板的花瓣開裂和翻轉現象；趙延杰等［2］通過開展近場水下爆炸試驗，同樣發現了固支圓板花瓣開裂外翻的毀傷模式；中國工程物理研究院的陳剛等［3］通過開展尖頭彈體侵徹實驗，研究了不同速度下彈體正穿甲、斜穿甲金屬板花瓣開裂毀傷模式。在理論研究方面，Zaid和Paul［4］依據動量理論推導了花瓣撕裂過程中所產生的動力功和彎曲能；Wierzbicki［5］依據 Nurick 和 Radford［1］開展的接觸爆炸載荷作用下板的一系列實驗，發展了新的花瓣開裂計算模型，并借助CTOD準則，通過對花瓣開裂后的彎曲能和撕裂能進行Hamilton變分計算，求出了花瓣開裂過程中的彎曲能和撕裂能；張振華等［6］根據花瓣彎曲運動模式，計算出了花瓣動能功率，并依據廣義Hamilton變分原理（即結構動能減小功率與塑性耗散能增加功率相等），最終求出了花瓣開裂后的彎曲能和撕裂能，其計算結果與 Wierzbicki［5］的基本一致，目前，該計算模型已基本被眾多學者認可。在數值仿真方面，國內外眾多學者對強沖擊載荷下的靶板花瓣開裂模式進行了數值仿真，所得結果與實驗結果在現象上基本吻合，但對花瓣成形過程中的機理揭示得較少。李營等［7］借助有限元軟件ABAQUS對薄板花瓣型破口形成過程進行了分析，指出花瓣型破口形成過程中裂縫區域應力狀態變化復雜，遠非傳統的單向受拉、雙向受拉［8-9］所能描述，必須計及不同應力三軸度下的材料失效準則。但由于該文獻中薄板計算模型采用的是Shell單元，該單元的應力三軸度描述區間被限制在［-0.66，0.66］之間，故所揭示的花瓣型破口形成過程具有一定的局限性。

本文將以前期開展的尖頭彈侵徹金屬靶板實驗為依據，針對靶板材料——Q345B鋼開展壓縮、扭轉、拉伸等力學性能實驗，獲取不同應力三軸度下的材料失效判據。然后，采用Solid單元建立彈體靶板計算模型，從花瓣型破口形成過程、典型區域應力狀態、不同斷裂準則等方面揭示尖頭彈體穿甲金屬板花瓣型破口形成過程。

1 尖頭彈穿甲金屬板實驗

尖頭彈穿甲金屬板實驗在南京理工大學的打靶實驗場開展。實驗中，尖頭彈殼體材料為高強度、高硬度的30CrMnSi，炸藥與引信材料采用PPS塑料替代；尖頭彈彈徑92 mm，彈長276 mm，殼體質量3.21 kg，填充物質量1.45 kg，總質量4.66 kg，如圖1所示。靶板材料為Q345B鋼，厚度為8 mm，尺寸為1 000 mm×1 000 mm，四周邊界通過M24螺栓與工裝架連接，螺栓間距為150 mm，靶板實際有效面積為700 mm×700 mm。

采用測速靶網測量尖頭彈穿甲前后的速度，尖頭彈入射速度為208 m/s，穿出速度為185 m/s，彈體在穿甲前、后幾乎未產生明顯的塑性變形。尖頭彈體穿透靶板后，形成了典型的花瓣型開裂毀傷模式，圖2所示為Q345B鋼靶板模型毀傷模式示意圖。由圖可見，靶板變形毀傷區域基本集中在彈孔附近，從靶板背面來看，共形成了4塊基本對稱的花瓣，花瓣裂縫間呈明顯的45°傾角，同時由于與尖頭彈的相互耦合作用，每塊花瓣頂端區域還存在著十分明顯的減薄和灼燒現象，單塊花瓣基本呈內凹狀態，且并未形成明顯的外翻現象，這與近場水下爆炸下形成的花瓣開裂模式具有一定的區別。

2 Q345B鋼斷裂力學性能實驗

為了獲取Q345B鋼在不同應力三軸度范圍內失效的判據，孟利平［10］利用 WDW-100DIII微機控制電子萬能試驗機開展了標準光滑圓棒、缺口試件拉伸實驗及圓柱壓縮實驗，利用NDW-500III微機控制電子扭轉試驗機開展了扭轉實驗，試件模型如圖3所示（圖中R表示試件缺口半徑）。其中，拉伸實驗在試件標距段安裝引伸計，引伸計標距50 mm，量程25 mm，每組實驗均進行了5次重復實驗，以保證實驗數據的有效性。

考慮到現階段扭轉試件斷裂應變尚未建立相對可靠的計算公式，為統一，本文借助有限元手段確定光滑圓棒、缺口試件、扭轉試件、壓縮試件的失效應變。有限元模型利用ABAQUS軟件建立，試件均采用二維軸對稱模型，一端固定，另一端施加位移/轉角載荷，同時不設置失效判據，當達到試件的實驗最大位移或者轉角時，取此時試件的最大等效塑性應變為斷裂應變。各類試件斷裂時刻的等效應變分布如圖4所示，試件斷裂應變取值如表1所示（表中，扭轉試件斷裂時刻的角度為45 rad）。

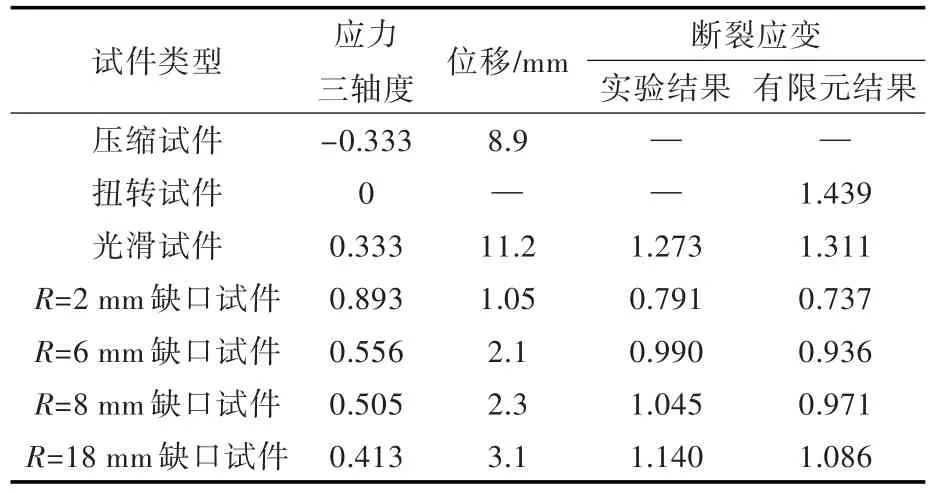
表1 不同試件斷裂時刻等效應變值Table 1 The equivalent strain of different experiment specimen when fractured

JC失效模型考慮了不同應力三軸度對失效應變的影響，是現階段穿甲數值仿真分析較理想的材料失效模型。僅考慮應力三軸度影響的JC的表達式如下：

式中：εf為材料等效塑性應變；為應力狀態參數，其中P為靜水壓力，σeff為等效應力，Rσ為應力三軸度。根據實驗結果，擬合得到D1=0.697 7，D2=2.781 1，D3=4.597 7。

3 花瓣型破口成形機理仿真分析

3.1 計算模型

根據尖頭彈穿甲8 mm金屬板實驗建立有限元模型（圖5），靶板采用Solid單元建立，彈靶碰撞區域網格尺寸為2 mm，其中尖頭彈網格數量為19.6萬，靶板模型網格數量為13.8萬。在計算過程中，彈體殼體和炸藥采用共節點方式連接并設置面面侵蝕接觸，尖頭彈和靶板也采用面面侵蝕接觸，接觸剛度系數為1.0。內部填充炸藥采用彈塑性模型，密度為1 400 kg/m3，彈性模量為60 GPa，屈服強度為30 MPa，失效應變為0.6。

殼體、Q345鋼采用JC強度模型和JC失效模型，其中JC強度模型的表達式為：

式中：為材料流動應力；A為靜態屈服應力，MPa；B為硬化參數，MPa；n為硬化指數；C為應變率參數；ε為塑性應變率；εx為參考應變率；T為溫度；Tr為室溫；Tm為熔化溫度；m為溫度軟化指數。

JC失效模型的表達式如下：

式中：

本文暫不考慮應變率、溫度對材料失效應變的影響，取D4=D5=0。Q345B鋼和戰斗部殼體材料的JC強度模型參數和JC失效模型參數如表2所示，參數是根據材料力學性能實驗進行擬合而得到，詳見文獻［11］。

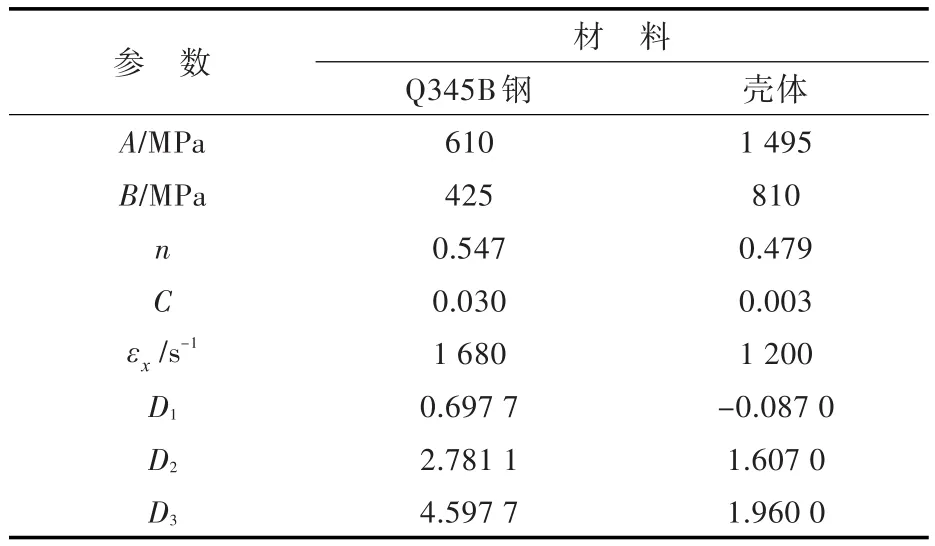
表2 戰斗部殼體和靶板材料JC強度模型和JC失效模型參數取值Table 2 Parameters of JC strength model and JC failure model for missile shell and target material

3.2 花瓣型破口形成過程分析

圖6所示為金屬板在尖頭彈侵徹過程中花瓣型破口形成過程示意圖。靶板最終形成了4塊基本對稱的花瓣模型，花瓣頂部存在明顯的減薄現象，花瓣的變形模型基本為內凹型，與實驗觀察到的現象基本一致。靶板花瓣型破口形成過程大體可分為以下4個階段：

1）碟形—隆起變形階段（0～0.18 ms）。靶板最先與尖頭彈接觸區域在撞擊力的作用下貼合于彈頭表面，與尖頭彈共同向前運動，接觸區域由于受力最大，變形十分明顯，非接觸區域在接觸區域速度的帶動下也開始發生隆起變形，因此產生了十分明顯的碟形—隆起變形模式，如圖6（a）所示。

2）尖頭彈體擴孔階段（0.18～0.27 ms）。尖頭彈頂端刺透靶板，形成初始破孔，同時由于尖頭彈體仍具有較大的速度，頭部將進一步向前運動，初始破孔不斷擴張，在塑性流動應力的作用下破孔周邊環向區域不斷減薄，靶板其他區域在與彈體的相互作用下繼續產生隆起變形，如圖6（b）所示。

3）花瓣型裂縫形成與擴張階段（0.27～0.90 ms）。當破孔周邊的環形應變達到失效應變時，裂縫開始從破口頂端形成，隨著尖頭彈的不斷侵入，裂縫逐步向外擴張形成花瓣，隨后，花瓣在彈體的繼續作用下開始向外翻轉，如圖6（c）和圖6（d）所示。若此時花瓣環向應變仍不斷增加且超過極限應變，單塊大花瓣將繼續撕裂形成子花瓣。

4）花瓣破口區域整體運動（0.9 ms至最后穩定）。當彈體施加在靶板上的沖擊不足以延續裂縫的擴張和花瓣的彎曲時，此時花瓣型破口區域在殘余動能的支撐下將產生整體的變形模式，來回震蕩直至動能消耗殆盡，如圖6（e）所示。

3.3 典型區域應力狀態分析

選取花瓣型破口裂紋擴展路徑典型位置單元的應力狀態進行分析，測點位置既包括裂縫形成區域失效單元，也包括裂紋擴展路徑方向未失效單元；既包括靶板迎撞面單元，也包括背板方向區域單元。圖7所示為單元測點位置示意圖。

圖8所示為花瓣型破口裂縫處典型失效單元的應力三軸度變化過程示意圖。編號為2185494，2187370和2199622的單元處于靶板迎彈面，編號為2185497，2187373和2199625的單元處于靶板背面。結合圖8可以發現：與彈體尖頭區域最先作用的單元2185494首先受到壓縮波的作用，應力狀態最先表現為壓縮狀態，其后轉變為拉剪狀態，當壓縮波傳遞至上方單元2185497時產生反射拉伸波，因此，該單元的受力狀態立即從壓縮狀態轉化為拉伸狀態并一直保持單軸拉伸狀態直至失效。距迎彈面中心單元有一定距離的2187370和2199622單元由于中心區域的隆起變形，最初基本處于拉伸狀態，而后當彈體尖頭表面與其接觸時，在尖頭彈體的壓縮作用下單元轉變為壓縮狀態。而距中心單元有一定的距離的2187373，2199625靶板背面單元由于中心區域隆起變形，在背面引起塑性鉸，致使其受力狀態最先處于壓縮狀態，當花瓣根部塑性鉸繼續往外擴展時，此后處于拉伸狀態。總體來看，單元在失效之前基本是在各種受力狀態中進行轉換，同一位置靶板背面單元往往先于迎彈面發生失效，單元失效前所處狀態基本為單軸拉伸狀態（應力三軸度Rσ≈0.33）。

圖9所示為擴展路徑塑性大變形區域典型單元的應力三軸度變化過程示意圖。編號為2170658，2190318和2165442的單元處于靶板迎彈面，編號為2170661，2190321和2165445的單元處于靶板背面。總體來看，雖然該區域未處于單元失效區域，但在初始階段單元應力狀態變化劇烈，這可能是由靶板模型拉伸波、剪切波和壓縮波的耦合作用所造成。應力三軸度變化區間基本處于［-0.33，0.33］范圍，即單軸壓縮與單軸拉伸之間。

3.4 不同斷裂準則分析

牟金磊和陳長海等［8-9］通過測量爆炸沖擊載荷作用下花瓣型破口裂紋處的厚度變化，根據單方向應變假設或者雙方向應變假設推測了試驗板的斷裂失效應變，并在數值仿真中采用了該應變作為失效應變。結合3.3節的分析可知，在本模型中，尖頭彈體穿甲產生的花瓣型破口裂縫處的失效單元在失效前的應力狀態基本處于單軸拉伸狀態，由此來看，測量裂紋處的厚度并反推材料的斷裂應變具有一定的科學性，因此，本節將對此進行進一步的驗證。計算模型與3.1節的一致，將Q345B鋼靶板材料失效參數設置為常數，分別取應力三軸度Rσ=0.33（單軸拉伸）對應的失效應變1.29和應力三軸度Rσ=0.66（雙軸拉伸）對應的失效應變0.827，即通過擬合Q345B鋼JC失效模型，將應力三軸度Rσ=0.33和0.66依次代入式（1）中,即可求出對應的失效應變。

圖10和圖11所示分別為將失效應變設為單軸拉伸對應的失效應變1.29及雙軸拉伸對應的失效應變0.827下的計算結果。從靶板毀傷來看，當采用第1種失效應變時，靶板同樣可以產生幾乎是對稱的4瓣花瓣型破口；而采用第2種失效應變時，靶板最終形成了8瓣花瓣型破口，與實驗結果相差較大。從剩余速度的角度來看，采用JC失效模型、單軸拉伸失效應變、雙軸拉伸失效應變的彈體剩余速度依次為172，170和177 m/s。由此可見，本模型采用單軸拉伸失效應變也可以得出與JC失效模型基本一致的結果。

為進一步分析單軸拉伸失效應變準則與JC失效準則所取得的基本一致的花瓣型破口計算結果是否對于任何尖頭彈穿甲計算都滿足，將薄板厚度減至4 mm，彈體入射速度、網格尺寸與前文保持一致，同樣設置了JC失效準則、單軸拉伸失效準則和雙軸拉伸失效準則這3種失效模式，計算結果如圖12所示。從失效模式上來看，本計算模型中JC失效準則與雙軸拉伸失效準則所獲取的毀傷模式基本相近，花瓣型破口裂成了4瓣花瓣，而單軸拉伸失效準則下的花瓣型破口卻裂成了5瓣花瓣；從彈體剩余速度來看，JC失效準則、單軸拉伸失效準則和雙軸拉伸失效準則的彈體剩余速度依次為196，193，198 m/s。

綜上可發現，花瓣型破口裂紋形成過程中的應力狀態變化復雜，采用常應變失效準則（單軸拉伸失效應變、雙軸拉伸失效應變等）難以較好地預測所有靶板模型的花瓣型破口形狀，必須計及不同應力三軸度損傷的失效準則。

4 進一步的探討

在現有花瓣開裂理論計算（Wierzbicki［5］和張振華等［6］）中，通常將裂縫處的失效應變取為0.3，但依據本文的計算結果來看，該取值方法具有一定的局限性，考慮到花瓣開裂撕裂過程中裂縫處的應力三軸度Rσ基本處于［0.33，0.66］之間，認為取二者對應的失效應變的平均值才具備一定的工程價值，即

式中：為應力三軸度Rσ=0.33時對應的失效應變；為應力三軸度為Rσ=0.66時對應的失效應變。

文獻［8］是通過測量裂紋附近板厚的減薄率來推算材料的失效判據，并將其直接用于后文的仿真評估計算，但其忽略了裂縫撕裂過程中應力狀態對失效應變的影響，因此得出的失效判據并不適用于所有撕裂過程。

5 結 論

本文以前期開展的尖頭彈穿甲Q345B金屬板形成花瓣型破口毀傷模式和不同應力狀態下Q345B鋼的斷裂力學性能實驗為依據，利用仿真手段對花瓣型破口成形機理進行了分析，得出如下結論：

1）尖頭彈體穿甲金屬板形成花瓣型破口的過程主要可以分為碟形—隆起變形階段、尖頭彈體擴孔階段、花瓣型裂縫形成與擴張階段及花瓣破口區域整體運動4個階段。

2）花瓣型破口裂紋形成過程中的應力狀態變化復雜，采用常應變失效準則（單軸拉伸失效應變、雙軸拉伸失效應變等）難以較好地預測所有靶板模型的花瓣型破口形狀，須計及不同應力三軸度損傷的失效準則。

3）對傳統的花瓣開裂理論評估方法中失效應變的取值進行了改進，結合本文的分析可知，取材料應力三軸度Rσ=0.33和0.66時對應的失效應變的平均值作為理論評估值才具有一定的工程應用價值。

4）通過測量裂紋附近處板厚的變化來反推材料的斷裂應變，還需考慮裂縫所處的應力三軸度，這樣得出的數據才有價值。

［1］NURICK G N，RADFORD A M.Deformation and tearing of clamped circular plates subjected to localized central blast load［J］.Recent Developments in Computational and Applied Mechanics，1977，13：276-301.

［2］趙延杰，潘建強，劉建湖.聚脲涂覆鋼板水下爆炸試驗研究［C］//第十一屆全國爆炸力學學術會議.珠海2016.

［3］陳剛，陳忠富，張方舉，等.截錐形彈體侵徹薄靶板實驗研究［J］. 彈箭與制導學報，2005，25（4）：888-890.CHEN G，CHEN Z F，ZHANG F J，et al.Investigation of truncated cylindroconical projectile penetrating thin target［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2005，25（4）：888-890（in Chinese）.

［4］ZAID M，PAUL B.Mechanics of high speed projectile perforation［J］.Journal of the Franklin Institute，1957，264（2）：117-126.

［5］WIERZBICKI T.Petalling of plates under explosive and impact loading［J］.International Journal of Impact Engineering，1999，22（9/10）：935-954.

［6］張振華，朱錫.剛塑性板在柱狀炸藥接觸爆炸載荷作用下的花瓣開裂研究［J］. 船舶力學，2004，8（5）：113-119.ZHANG Z H，ZHU X.Petaling of rigid plastic plate under contact explosive loading of cylindrical dynamite［J］.Journal of Ship Mechanics，2004，8（5）：113-119（in Chinese）.

［7］李營，吳衛國，張磊，等.基于多軸應力損傷的薄板花瓣型破口形成機理研究［J］.爆炸與沖擊，2017，37（3）：554-559.LI Y，WU W G，ZHANG L，et al.Mechanism research of thin plate petaling under local loading based on multiaxial stress damage［J］.Explosion and Shock Waves，2017，37（3）：554-559（in Chinese）.

［8］牟金磊，朱錫，張振華，等.水下爆炸載荷作用下加筋板變形及開裂試驗研究［J］.振動與沖擊，2008，27（1）：57-60.MU J L，ZHU X，ZHANG Z H，et al.Experimental study on deformation and rupture of stiffened plates subjected to underwater shock［J］.Journal of Vibration and Shock，2008，27（1）：57-60（in Chinese）.

［9］陳長海，朱錫，侯海量，等.近距空爆載荷作用下固支方板的變形及破壞模式［J］.爆炸與沖擊，2012，32（4）：368-375.CHEN C H，ZHU X，HOU H L，et al.Deformation and failure modes of clamped square plates under close-range air blast loads［J］.Explosion and Shock Waves，2012，32（4）：368-375（in Chinese）.

［10］孟利平.應變率和應力三軸度對船用鋼變形和斷裂的影響研究［D］.無錫：中國船舶科學研究中心，2016.

［11］伍星星.大質量戰斗部穿甲數值仿真對材料斷裂極限參數確定分析［C］//第十五屆戰斗部與毀傷會議集.北京，2017.