非平穩強噪條件下的視頻相位放大技術研究

,

(中國科學技術大學精密機械與精密儀器系，安徽 合肥 230026)

0 引言

使用高速相機拍攝視頻分析物體的振動，相比傳統接觸式測量不會帶來質量負荷，而且成本更低，分辨率更高。但是有時物體的振動很微弱，對于人眼來說很難察覺，需要放大后才能更好地觀察。傳統的線性歐拉放大技術[1]在高空間頻率時只能放大較小的倍數，并且當放大倍數增大時，噪聲也會被放大。

Wadhwa提出了基于復數金字塔的視頻運動處理技術[2-3]，依據在圖像的一個空間子帶中復數金字塔的相位變化正比于局部運動的原理[4]，計算局部相位的變化并對選定的頻率范圍做帶通處理，再將放大處理后的信號重構為視頻。這種基于相位的方法可以達到更大的放大倍數和更好的噪聲表現。但是這種方法在處理非平穩信號時，帶通濾波器需要選擇較大的頻帶范圍，在此頻帶范圍內存在的噪聲也將被放大，所以需要更好的方法來處理寬頻帶內的噪聲。時頻濾波[5]是一個比較理想的選擇。同時對每個像素點進行時頻處理會大大增加計算量，降低運算速度。

在此，提出了一種基于參數化時頻分析[6]及主成分分析(PCA)[7]的濾波方法，來放大非平穩強噪視頻信號。相比于傳統相位視頻放大技術，這種方法可以有效提取非平穩信號并實現原始視頻信號的放大。

1 時變視頻相位放大技術

1.1 相位放大原理

在空域，根據復數可控金字塔原理，將圖像序列I(m,n,t)多分辨率分解為：

A(γ,θ,m,n,t)eiψ(γ,θ,m,n,t)

(1)

γ表示尺度；θ表示方向。在時域，依據t0時刻的相位可以計算出t時刻的相位變化量：

δ(γ,θ,m,n,t)=ψ(γ,θ,m,n,t)-ψ(γ,θ,m,n,t0)

(2)

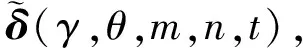
(3)

但是這種方法在處理非平穩信號時，往往需要選擇較大的帶寬，此帶寬內的噪聲信號也將會被放大，此時就無法有效地提取所需要的信號，所以要從時頻角度來分析提取信號。在此之前，需要了解信號時頻分布類型，才能選擇有效的濾波器。

根據Davis的研究，對相位變化信號進行幅值加權，可以得到局部振動信號：

Φi(γ,θ,t)=∑m,nA(γ,θ,m,n,t)2δ(γ,θ,m,n,t)

(4)

那么進一步，可以得到全局振動信號：

(5)

1.2 PCA降維和時頻濾波

通過復數金字塔可以將各尺度方向上相位隨時間變化的信號δ(m,n,t)提取出來，但是對每個像素點的δ時頻變換，計算量巨大，耗時嚴重。為解決這個問題，采用PCA將δ降維，對降維后的信號做時頻處理。將時刻j的δ重排為一列向量δj∈RK×1，其中K=M×N，則δ(m,n,t)可以表示為：

X=[δ1,δ2,δ3,…,δT]

(6)

PCA分解是指對矩陣X∈RK×T，存在特征向量矩陣U∈RK×K和特征值矩陣D∈RK×K滿足下列方程：

XX′=UDU′

(7)

將特征向量按對應特征值大小從上到下按行排列成矩陣，取其前r行組成矩陣P∈Rr×K，那么就可以得到降維到r維后的數據：

Y=PX

(8)

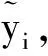
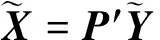
(9)

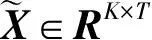
1.3 算法流程

基于參數化時頻分析和PCA降維處理原理，提出了針對非平穩強噪聲的視頻相位放大技術。具體流程如圖1所示，算法描述如下：

a.將視頻信號I通過復數金字塔分解，提取圖像相位信號ψ和幅值信號A。

b.對相位信號ψ在時間維度上做差分求出相位變化信號δ，對其幅值加權求和，得到對應尺度方向上的局部振幅Φ，再對各尺度方向求和得到全局振幅s(t)。

c.對s(t)做參數化時頻分析，得到時頻脊線函數，選擇帶寬，構造時頻模板ymask。

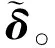
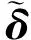
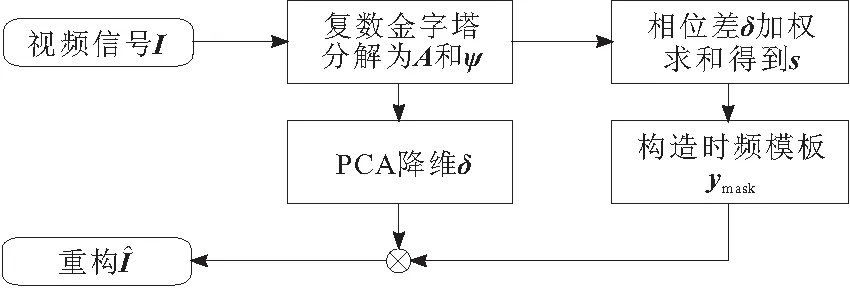
圖1 時變視頻放大方法流程

2 實驗分析

2.1 轉子振動信號采集實驗

實驗數據采集平臺如圖2所示。振動信號采集系統包括Basler acA2000高速攝像機、光源、轉子實驗臺和臺式機電腦。轉子實驗臺電機為三相異步電機，型號為YE2-8012，電機驅動器型號為MICROMASTER440。

設置電機最高轉速為3 000 r/min，依據驅動器設置電機將在10 s內勻減速至停止。實驗中，相機分辨率設置為400像素×1 024像素，采樣率為392 Hz，一次采樣3 000幀。

圖2 實驗設備

2.2 振動信號提取分析

根據Davis的方法，分析得到電機降速過程中轉子振動信號的波形如圖3所示，對其做STFT，可以看出振動頻率隨時間近似線性減小，但是在27 Hz處存在能量較高的干擾頻率，嚴重影響視頻相位放大的結果。

用多項式參數化時頻分析方法處理該信號，假設其時頻函數為：

f(t)=z0+z1t+z2t2+z3t3

(10)

求得z0=36.627 5，z1=-5.096 2，z2=-0.002 9，z3=0.008 9，其斜率與實際頻率變化率5 Hz近似一致。選取圖像金字塔分解得到的某一尺度、方向上圖像一像素點的相位變換信號δ進行時頻分析，其波形及時頻如圖4所示。

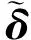
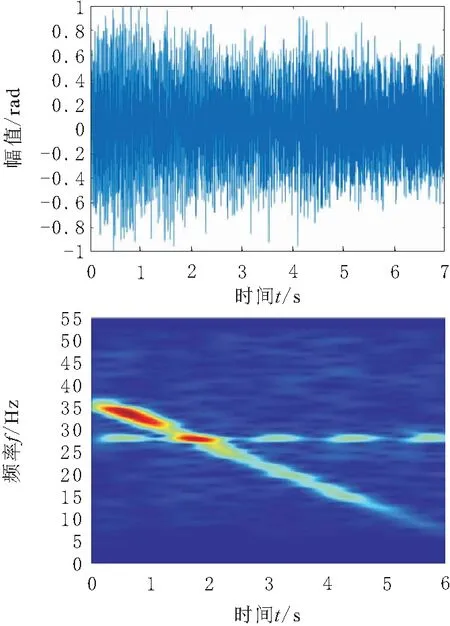
圖3 視頻麥克風信號波形和時頻

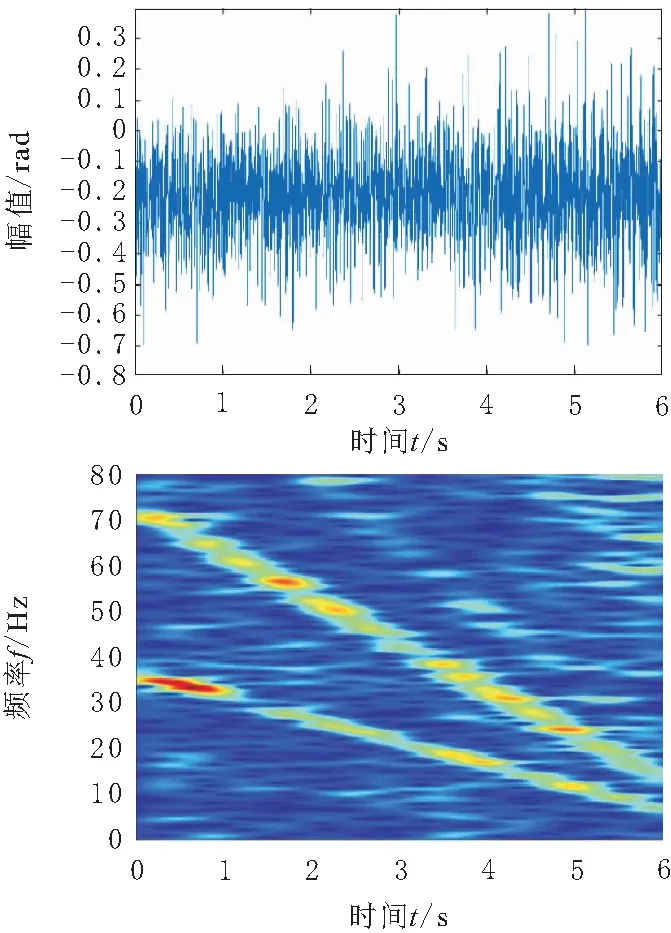
圖4 原始相位變化波形與時頻

設置放大系數12倍，對濾波后的相變信號重構，得到重構視頻。放大前和放大12倍后視頻對應幀對比如圖6所示，其中，上圖表示放大處理前的原始視頻圖片，下圖表示放大處理后的視頻圖片。圖6a表示處理前后視頻對應幀圖像，由于處理時為加快運行速度，對圖像做了縮放，所以下圖相對模糊。圖6b表示取視頻在100～300幀(0.255～0.765 s)的切片組成的圖片，可以看出處理后軸發生明顯振動，并且振動頻率較快。圖6c表示視頻在1 800～2 000幀(4.592～5.102 s)的切片組成的圖片，可以看出電機轉速降低后，對應的振動頻率也變慢了。

在MATLAB2017中，在沒有使用PCA方法時，直接對各像素點時頻濾波，在單一尺度、方向上運算時間超過半小時，而使用PCA降維處理，則運算時間降低至130 s左右，說明PCA方法有效降低運算量，大大提高運行速度。

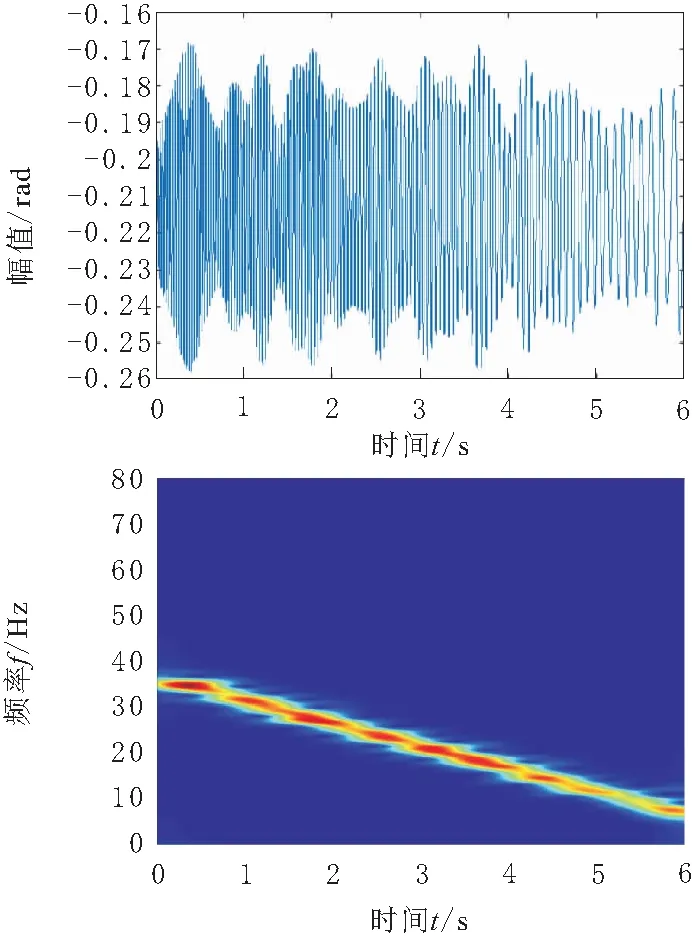
圖5 降維濾波后信號波形與時頻

圖6 處理前后圖像對比

3 結束語

提出了一種基于參數化時頻分析和PCA降維算法的視頻相位放大方法，用于將物體的微小振動放大，便于觀察和分析。相比于傳統的視頻相位放大方法，所提方法更加針對非平穩振動信號，因此，該方法在消除噪聲干擾和放大非平穩信號上具有明顯優勢。實驗結果表明，該方法能有效地提取電機降速過程中轉子振動頻率，并可將視頻中轉子振幅放大。

參考文獻：

[1] Fuchs M, Chen T, Wang O, et al. Real-time temporal shaping of high-speed video streams[J]. Computers and Graphics, 2010, 34(5): 575-584.

[2] Simoncelli E P, Freeman W T.The steerable pyramid: a flexible architecture for multi-scale derivative computation[C]// Proceedings of the IEEE International Conference on image Processing，1995, 3: 444-447.

[3] Wadhwa N,Rubinstein M,Durand F,et al.Phase-based video motion processing[J]. ACM Transactions on Graphics (TOG), 2013, 32(4): 80.

[4] Davis A,Rubinstein M,Wadhwa N, et al. The visual microphone: passive recovery of sound from video[J].ACM Transactions on Graphics (TOG),2014,33(4): 79.

[5] 李燕,魏宗信,劉軍.機電系統振動信號分析技術的研究[J].機械與電子,2010(2):30-32.

[6] 楊揚.參數化時頻分析理論、方法及其在工程信號分析中的應用[D].上海：上海交通大學,2013.

[7] Yang Y, Dorn C, Mancini T, et al. Blind identification of full-field vibration modes from video measurements with phase-based video motion magnification[J]. Mechanical Systems and Signal Processing, 2017, 85: 567-590.