基于逆變電源組網的電力系統短路電流改進算法

王云帆，徐正喜，吳大立

(武漢第二船舶設計研究所，湖北 武漢 430205)

0 引 言

船舶電力系統的短路電流計算是制定電力系統保護策略、斷路器整定以及設備選擇校驗的重要依據[1]。傳統交流電力系統的短路電流計算方法有很多，如GJB-173法、GB-3321法、IEC-60363和改進的IEC-61363等，基于每種方法不同的近似和假設，計算結果也不盡相同。

隨著艦船電力系統向集成化方向轉型，綜合電力系統成為未來艦船動力系統的發展方向[2]。直流電制以其功率密度大、配電效率高等優點[3]，成為目前綜合電力系統組網形式的重要研究方向。在采用直流電制的綜合電力系統中，一次側直流電網經逆變電源進行電能DC/AC變換后再組網供給交流負載使用，逆變電源取代了傳統的交流發電機成為了交流電網的主電源，其輸出短路電流數量級大大減小。

目前對電動機反饋短路電流算法的研究多集中于對單臺電動機精確算法的分析，文獻[4-5]總結了常用的感應電動機反饋電流計算公式并對各種算法的計算結果與物理實驗進行對比，文獻[6]討論了各種因素對反饋電流的影響。而對電動機群反饋電流計算多采用各標準中的近似算法。在由傳統發電機供電的交流電網中，電動機群饋送的短路電流相較于發電機輸出的短路電流只占較小的比例，因此傳統近似算法的誤差相對于總短路電流而言可以忽略，而逆變電源成為主電源后，短路電流數量級大大減小，傳統近似算法的相對誤差被放大不容忽略，目前極少有文獻對該問題進行討論。

本文首先分析了逆變電源相較于傳統發電機在短路時輸出特性的區別，然后提出了適用于逆變電源組網的電力系統中電動機群反饋電流的改進算法，通過仿真驗證了該改進算法相對于傳統算法的優越性。

1 電源短路特性分析

對于船舶交流電力系統，短路電流主要來自于系統電源提供的短路電流和電動機饋送的反饋電流。下面首先對發電機和逆變電源這2種系統電源在短路時的特點進行分析。

1.1 發電機短路特性

傳統交流發電機是船舶電力系統的短路電流主要供給源，系統發生三相短路故障的瞬間，由于磁鏈不能突變，同步電機的勵磁繞組和阻尼繞組內將感應出非周期電流以抑制電樞去磁效應，由于定轉子互相影響，電樞繞組激磁電動勢迅速增大，導致定子電流周期分量幅值迅速增大，即產生非常大的次暫態電流，再經次暫態和暫態過程衰減為穩態短路電流。同時同步電機的定子繞組為保持三相繞組磁鏈守恒，短路瞬間將感應出短路電流非周期分量（凸極機還有倍頻分量），隨定子繞組時間常數衰減。短路電流周期分量，非周期分量的合成即為短路瞬間同步發電機所提供的短路電流。

對發電機短路電流的計算可按照不同精度要求參照相應標準來進行[7]。由于在短路過程中，發電機輸出短路電流僅受到非常小的電樞阻抗和系統線路阻抗的限制，短路電流幅值非常大，可達到發電機額定電流的10倍以上。

1.2 逆變電源短路特性

典型的三相逆變電路拓撲結構如圖1所示，IGBT是三相逆變橋的主要工作器件，控制系統通過控制其依次通斷來實現直流到交流的逆變。

由于逆變電源的主要工作器件IGBT大電流耐受能力有限，短路發生時，逆變電源會由正常運行時的恒壓模式迅速進入故障限流模式，將輸出短路電流限制在一定數值以下，以保護電力電子器件不受損壞。

逆變電源工作模式之間的轉換如圖2所示，正常運行時，逆變電源以恒壓模式運行。短路發生瞬間，其輸出電流急劇增大，硬件限流電路將輸出短路電流限定在一個固定范圍內，同時軟件限流啟動，控制系統將逆變電源的輸出由電壓閉環控制切換為電流閉環控制，迅速降低逆變電源輸出電壓以維持輸出電流為一恒定值[8]，以恒流源模式工作。若故障在時間T以內被隔離或清除，則逆變電源恢復為恒壓模式，當故障維持時間超過控制系統預設值T時，逆變電源保護停機。

1.3 逆變電源短路電流計算

由以上逆變電源的控制原理可知，在電力系統中任何部位發生短路故障時，逆變電源的短路輸出電流值只取決于控制系統，且始終維持在一恒定數值，而與短路點位置和系統阻抗無關。這個限流值一般設定為逆變電源額定工作電流的1.5～3倍左右，是系統保護需求與IGBT器件的容量之間的平衡。

因此逆變電源穩態短路電流即其輸出限流值，本文以Is表示。由于逆變電源軟件限流啟動后需要半個到一個周波的時間才能達到穩態，短路瞬間逆變電源輸出短路電流會產生尖峰，在計算短路發生后第1個半波的短路沖擊電流時，根據需要可在穩態限流輸出值Is的基礎上乘以1.1～1.3倍的系數。

2 電動機短路特性分析

船舶電力系統中的電動機負載是短路電流的另一供給源。這是由于短路發生時，電網電壓驟降，而電動機由于慣性仍然保持轉動（短時內其轉速的變化相較于電磁暫態過程幾乎可以忽略），同時和轉子導體相交鏈的磁鏈不能突變，轉子繼續切割磁感線產生感應電勢，當電網電壓低于感應電勢時，電動機向短路點饋送短路電流。

分析異步電動機的三相短路過程時，可將它看作具有阻尼繞組（相當于轉子繞組）而沒有勵磁繞組的同步電機。由于異步電動機沒有勵磁繞組，其短路過程中只有次暫態過程。則其短路電流由定子電流周期分量（次暫態電流）和非周期分量組成。

基于以上對短路物理過程的定性分析，對異步電動機短路電流的計算式進行推導，近似認為角速度ω′=1，各物理量用標幺值表示。經繞組折算和頻率折算，可得異步電動機等值電路如圖3所示。

定子端點三相短路時，由基爾霍夫電壓定律有：

式中：Rs，Rr，Ls，Lr分別為定子，轉子繞組的電阻和電感系數；is，ir分別為定子，轉子繞組的電流；M為定子、轉子繞組間的互感系數。

該齊次微分方程的解由周期分量和非周期分量組成，倆者均為自由分量，按各自的時間常數衰減至0。設電源合閘角為0，電動機反饋電流可由式（2）表示。

式中：In0為短路電流非周期分量起始值；I′為短路電流周期分量起始值；Tdc為轉子繞組短路時定子繞組的時間常數，可由圖4所示等值電路計算；Tac′為定子繞組短路時轉子繞組的時間常數，可由圖5所示等值電路計算。

對于穩態運行時的電動機，有電壓方程如下：

式中：為定子電流周期分量有效值；為定子端電壓；為次暫態電勢，短路前后其值不會突變。r和可由圖3所示等值電路計算。

短路前瞬間，t=0–s時，根據式（3）定子電流可表示為：

當定子端點處發生短路時，短路后瞬間t=0+s時，電動機周期分量的初始幅值為：

此時總短路電流為：

由于短路前后電流不能突變，應等于，又短路前后電動機的次暫態電勢不突變。聯立上式即可解得電動機反饋電流為：

反饋電流由非周期分量和周期分量組成。該解析式結果與前文物理分析完全吻合。

3 電動機反饋電流改進算法

3.1 傳統短路電流計算方法誤差

傳統短路電流計算方法中采用近似方法計算運行中電動機群所饋送的短路電流。以GB3321為例，對功率100 kW以下的電動機群，采用等效平均電動機算法，將所有運行中的電動機等效成1臺直接接于主匯流排的等效電動機。等效電動機參數按照其平均功率根據國產電動機參數表選取，再由等效電動機參數，按照式（8）～式（10）進行計算。

1） 短路電流周期分量

2）短路電流非周期分量

3）最大非對稱短路電流

這種近似算法以主匯流排電壓VN代替電機次暫態電勢，忽略了負載電流的影響；并且忽略了線路阻抗，將導致短路電流計算結果偏大。在基于逆變電源組網的電力系統中，由于總短路電流數量級驟降，該近似方法所帶來的誤差不容忽略。

3.2 考慮負載電流影響的改進算法

根據逆變電源的短路限流輸出特性，本文提出將線路電纜阻抗和穩態負載電流計入反饋電流計算過程的改進算法。

由式（3）可知，電機穩態運行時，電流流經電樞阻抗將產生壓降，其內電勢將低于端電壓，傳統近似算法中忽略了該負載電流的影響。

即使是電機空載運行，由于異步電動機存在氣隙，亦需要較大的勵磁電流來產生所需主磁通，其空載電流在額定電流的20%～40%之間，電機容量越小，空載電流百分比越大，小型電機可達60%[9]。所以即使電動機空載運行，電流的影響仍不宜忽略。

為減小誤差，應計入負載電流的影響。通常系統運行電流未知，可根據系統運行總功率PN和電壓按照式（11）進行估算，電動機群空載運行時空載電流I0可由式（12）近似。將負載電流代入式（3）即可計算出電動機內電勢。

3.3 計入電纜阻抗的改進算法

由第2節中對異步電動機短路原理的推導可知計入線路電纜阻抗后，將對短路電流各分量起始值和非周期分量衰減常數產生影響。

1）電纜阻抗對短路電流起始值的影響

在傳統交流發電機供電的電網中，發電機與等效電動機并聯向短路點提供短路電流，外線路阻抗需根據混聯電路等效原理進行等效分別計入發電機和電動機支路[10]，計算過程較復雜。而在基于逆變電源組網的交流電網中，由于逆變電源在短路過程中相當于恒流源輸出，則短路時系統等效電路如圖6所示。圖中Rl，Xl為電纜阻抗。

由該等效電路，根據電路原理知識，可得計入電纜阻抗后的短路電流周期分量起始值如下：

根據第2節中的原理推導，非周期分量起始值按照式（14）計算，可近似認為與周期分量起始值相同。

2）電纜阻抗對衰減時間常數的影響

計入電纜阻抗后，計算非周期分量和周期分量衰減時間常數的等值電路如圖7和圖8所示。

則有：

綜上，由式（3）和式（11）可計算得電機次暫態電勢E″，將E″代入式（13）～式（16）可計算出修正后的短路電流起始值和各分量衰減常數。短路沖擊電流出現在短路后第1個半周波即0.01 s時（此時周期分量最大而非周期分量衰減有限），令t=0.01 s，再根據式（10）即可計算出短路沖擊電流，

4 仿真分析與算例驗證

由于船舶電力系統中電動機數量眾多且短路試驗破壞性大，本文在Matlab/Simulink中搭建逆變電源和電力系統仿真模型來模擬短路故障，以此對本文所提出的電動機反饋電流改進算法進行對比驗證。該仿真模型已對逆變電源和單臺電動機短路試驗結果進行擬合，仿真結果可信度高。

基于逆變電源組網的典型船舶電力系統如圖9所示，多臺逆變電源通過母聯開關可并聯或分別獨立運行，負載以放射狀結構分級分布。

搭建圖9所示仿真模型，2臺逆變電源分左右兩舷獨立運行，全船總功率877 kW，逆變電源短路限流輸出限流值3 000 A。仿真模型中計入線路阻抗，按照電動機功率對各支路進行電纜選型，再根據各支路電纜截面積和長度計算電纜阻抗值，等效成集中阻抗參數計入仿真模型。各電動機空載運行，短路合閘角設為a相電壓過零點，短路電阻10 mΩ。系統運行至0.54 s時在F1處發生三相短路，分別觀察左右兩舷電動機群的反饋電流。

短路后逆變電源輸出電流仿真結果如圖10所示，電動機群反饋電流仿真結果如圖11所示。由圖10可知，短路故障發生后，逆變電源恒流輸出，穩態短路限流有效值為3 000 A。短路瞬間逆變電源輸出電流有尖峰產生，但經計算驗證對反饋電流計算結果影響可以忽略。圖11所示電動機群反饋電流在短路后10 ms時達到最大，隨后迅速衰減，由于左舷相對右舷電動機群總功率更大，因而反饋電流峰值更高。

分別通過GB3321中傳統短路電流計算方法和本文改進算法對電動機群反饋電流峰值進行計算，并與仿真結果進行對比，結果見表1。為簡化后續論述，將傳統短路電流計算方法簡稱為船標算法，Ik表示短路沖擊電流。

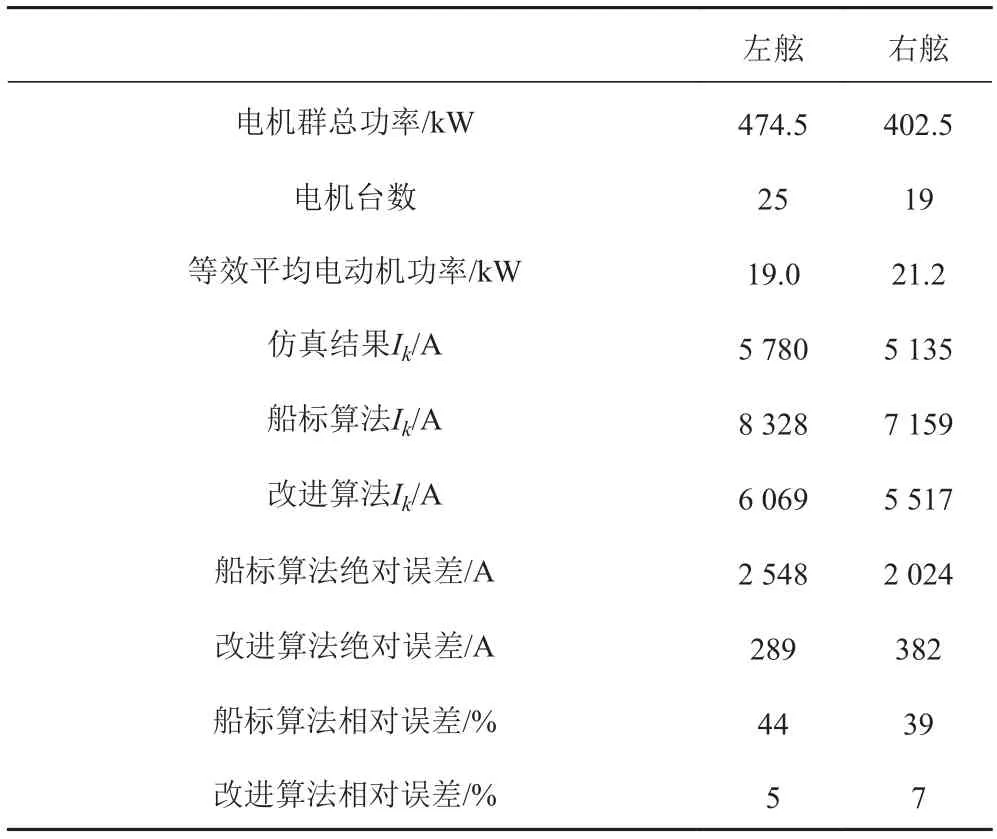
表1 船標算法、改進算法與仿真結果對比Tab.1 Comparison of improved method and GB3321 vs simulation results

由表1可見，船標算法的計算結果遠大于仿真結果，相對誤差達44%和39%，絕對誤差數量級與逆變電源輸出短路電流數量級相當，不可忽略。而通過本文改進算法相對誤差分別降低至5%和7%。仿真結果驗證了本文改進算法的有效性。

5 結 語

針對逆變電源組網的電力系統中傳統短路電流計算方法相對誤差較大的問題，本文提出了電動機反饋電流的改進算法，較傳統算法精度顯著提高，對逆變電源組網的電力系統中短路電流計算具有重要實用意義。

[1]王寓, 王主丁, 張宗益.國內外常用短路電流計算標準和方法的比較研究[J].電力系統保護控制, 2010, 38(20):148–152.

[2]馬偉明.艦船動力發展的方向——綜合電力系統[J].海軍工程大學學報, 2004, 14(6): 1–11.

[3]DENG Q, LIU X, SOMAN R, et al.Primary and backup protection for fault current limited MVDC shipboard power systems[C]// IEEE Ests.2015: 40–47.

[4]MALJKOVIC'Z, CETTOLO M, PAVLICA M.The impact of the induction motor on short-circuit current[J].IEEE Industry Applications Magazine, 2001, 7(4): 11–17.

[5]劉楠, 張彥濤.感應電動機負荷對短路電流影響機理研究[J].電網技術, 2012, 36(8): 187–192.LIU Nan, ZHANG Yan-tao.Impact of load induction motor on power system short-circuit current calculation[J].Power System Technology, 2012, 36(8): 187–192.

[6]XU Hui-yi.Feedback current impact to distribution network of large capacity motor users[C]// International Conference on EProduct E-Service and E-Entertainment, 2010: 1–3.

[7]吳忠林.船舶交流電力系統的短路電流[M].北京: 國防工業出版社, 1983.

[8]柳彬, 謝煒, 余躍聽, 等.逆變電源短路保護及限流策略[J].艦船科學技術, 2011, 33(8): 95–98.LIU Bin, XIE Wei.YU Yue-ting, et al Research on inverter short-ciruit protection and current-limiting strategy[J].Ship Science and Technology, 2011, 33(8): 95–98.

[9]潘再平.電機學[M].杭州: 浙江大學出版社, 2008.8.

[10]張志, 彭曉濤, 李曉寧, 等.改進的多母線船舶電力系統短路電流計算方法[J].電網技術, 2013, 37(8): 2212–2217.ZHANG Zhi, PENG Xiao-tao, LI Xiao-ning, et al.An improved short-circuit current calculation method for multi-bus ship power system[J].Power System Technology, 2013, 37(8):2212–2217.