百葉風口的對開張角對室內熱舒適性及能耗影響分析

劉鵬飛，陳煥新?，王江宇，雷艷杰，張軍，孫策

（1-華中科技大學能源與動力工程學院，湖北武漢 430074；2-北京華譽能源技術股份有限公司，北京 100083）

0 引言

隨著社會的快速進步和經濟的迅猛發展，人們的經濟水平不斷提高，這也使得人們對生活環境有了更高水平的要求。現如今，人們的大部分時間都是在室內度過，而室內環境質量的優劣取決于室內氣流組織的分布。我國國家標準《采暖通風與空氣調節設計規范》[1]規定，舒適空調室內溫、濕度參數如下：夏季溫度24 ℃～28 ℃，濕度40%～65%，空氣流速小于0.3 m/s。

1 模型的建立

1.1 物理模型

本文所研究的空調辦公室房間尺寸為5.5 m×4.0 m×3.5 m，中央空調的單層百葉風口位于房間左側，其尺寸為0.8 m×0.2 m，回風口尺寸0.8 m×0.2 m，辦公桌尺寸為2.0 m×1.5 m×0.8 m，書柜緊貼墻壁，對室內氣流組織影響較小，故不予考慮，日光燈管由于體積較小，且一般白天不開，故忽略。工作人員兩名，大部分時間人員靜坐在電腦前，而電腦體積較小，為簡化模型，將電腦和人體一同等效為一個長方體，等效尺寸為0.6 m×0.3 m×1.2 m，其熱流密度為100 W/m2，整體模型如圖1所示。

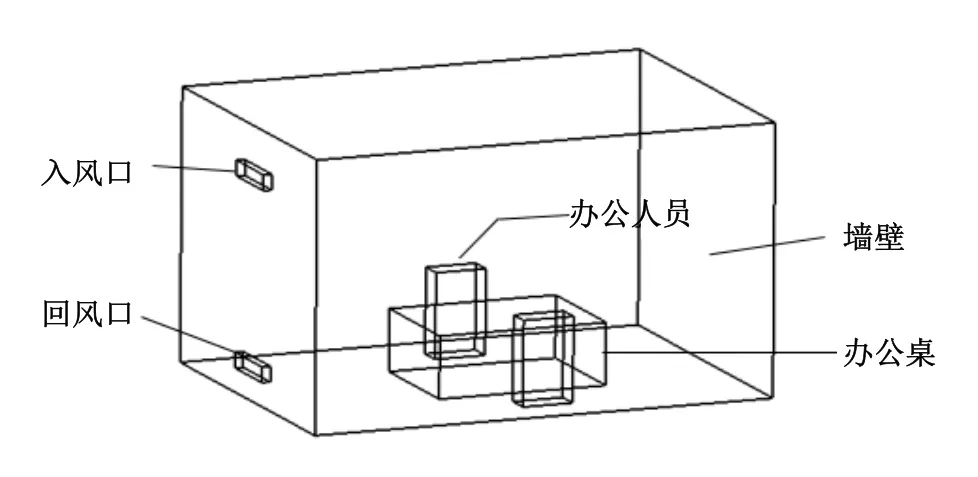
圖1 房間模型圖

1.2 風口模型

空調通風房間實際的送風口幾何形狀很復雜，其入口的邊界條件往往難以直接描述。目前描述風口的模型眾多，各有優缺點，本文以“N點風口動量模型”為基礎，結合“局部定義法”來描述百葉風口。

N點風口動量模型使用N個簡單的開口代替不同出流方向，從而簡化對入流邊界條件的描述，對于N的取值，則需要視出流條件而定。但N點動量風口模型只能實現于清華大學自主開發的三維通用CFD軟件STACH-3中，一般的CFD軟件或者傳統的流體流動數值模擬算法都無法實現[21]。局部定義法則是傅斌在“N點風口動量模型”的基礎之上，使用相應的算法，使之能夠在商用CFD軟件上實現。

在本文中，百葉風口的尺寸為0.8 m×0.2 m，有效面積系數為0.75，出流方向分為兩種情況，即N=1和N=3。當N=1時，出流方向角度為0°；N=3時，葉片對開，目前市面上常見的對開角度分別為20°、30°以及45°。圖2為典型百葉風口送風示意圖。

圖2 典型百葉送風口送風示意圖

1.3 數學模型

標準κ-ε湍流模型在工程運用上的準確性已經得到了大量的實驗驗證，精度可靠，且對于大渦模擬等，計算量要小很多[11]。為此需要如下假設：

1）室內空氣低速流動，為不可壓縮流體且符合Boussinesq假設；

2）流動為穩態流動，在入口處送風射流參數均勻，室內空氣物性為定值；

1.2 方法 對照組孕產婦無定期產檢，按照個人意愿進行保健措施。觀察組孕產婦嚴格按照下述原則執行孕期保健：①孕產婦早孕期首診時建立電子孕產婦保健系統檔案，并給予孕婦孕產期保健手冊；②定期發放相關宣傳資料，定期開辦孕婦學校及講座；③制定產檢計劃，及時發現相關并發癥、合并癥并給予積極處理；④對胎兒實施監護，了解胎兒宮內生長狀況、有無發育畸形等。

3）空調開啟時，門窗一般都處于緊閉狀態，故不考慮漏風的影響；

4）忽略四周墻壁及室內物體的輻射熱，忽略能量方程中由于粘性作用引起的能量耗散。

2 網格劃分及邊界條件

2.1 網格劃分

辦公室空調房間送風口為百葉風口，辦公室內實際的百葉風口的尺寸為0.8 m×0.2 m，有效面積系數為0.75，所以模型中的百葉風口尺寸為0.60 m×0.15 m。網格質量的高低是影響計算精度的一個重大影響因素，高質量的網格往往能夠加快收斂速度，得到更精確的解。本文借助網格劃分軟件ICEM，采用結構化網格劃分計算域，網格質量最低為0.905，網格數量為920,915，圖3為網格劃分圖。

圖3 網格劃分圖

2.2 邊界條件的設置

1）入口邊界：送風口定義為速度入口，根據《暖通空調送風風速標準》中規定百葉風口的送風速度為2.5 m/s～4 m/s，為了減小吹風感，選取風口頸部的送風速度2.5 m/s，兩側風口的出風速度按照文獻[21]中的公式進行計算，室內設定溫度為26 ℃，送風溫度為23 ℃，方向分別為0°、20°、30°、45°。根據相應的公式計算出湍流強度I為4.20%，湍流粘度比ut/u為86.54。

2）出口邊界：回風口定義為自由出流。

3）壁面邊界：空調房內壁面邊界設為恒溫邊界，按照如圖2所示方位，前面的墻壁由于直接吸收太陽的輻射，溫度較高，溫度T為309.15 K，后墻靠近走廊，溫度T為301.15 K，其余四面墻壁由于和其他空調房間相連，均視為絕熱壁面；電腦與人同為熱源體，等效熱流密度為100 W/m2。辦公桌不散發熱量，僅作為障礙物處理。

4）計算模型選用標準κ-ε兩方程紊流模型，近壁面區域選用標準壁面函數法，采用SIMPLE算法。

邊界條件設置完成以后，在空調房間內設立3個監測點，以便觀測房間內流場的收斂情況，作為判斷收斂的主要依據。3個監測點的坐標分別為：point-1（2.75，2，1.1），point-2（1.25，2，1.1），point-3（4.25，2，1.1）。

3 模擬結果與分析

3.1 室內溫度場與速度場分析

由于人體的溫度敏感區位于頭部和腳踝處，室內人員坐姿時頭部的高度約1.1 m，腳踝處高度約為0.1 m。因此，選取這兩個截面的溫度和速度分布來評判室內的熱舒適度。

圖4～圖7分別為對開角度為0°、20°、30°和45°時室內溫度場與速度場的分布情況。

圖4 對開角度為0°時溫度和速度分布云圖

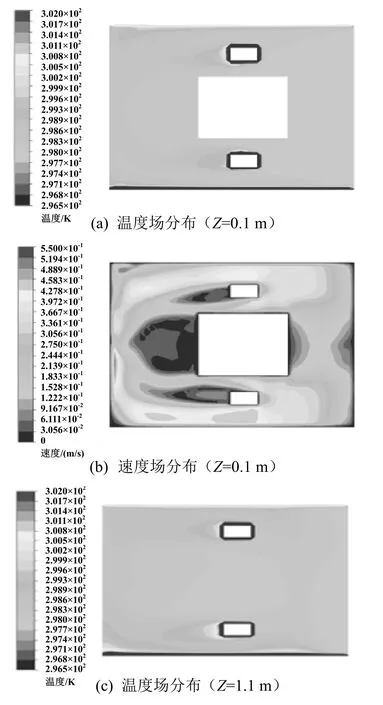
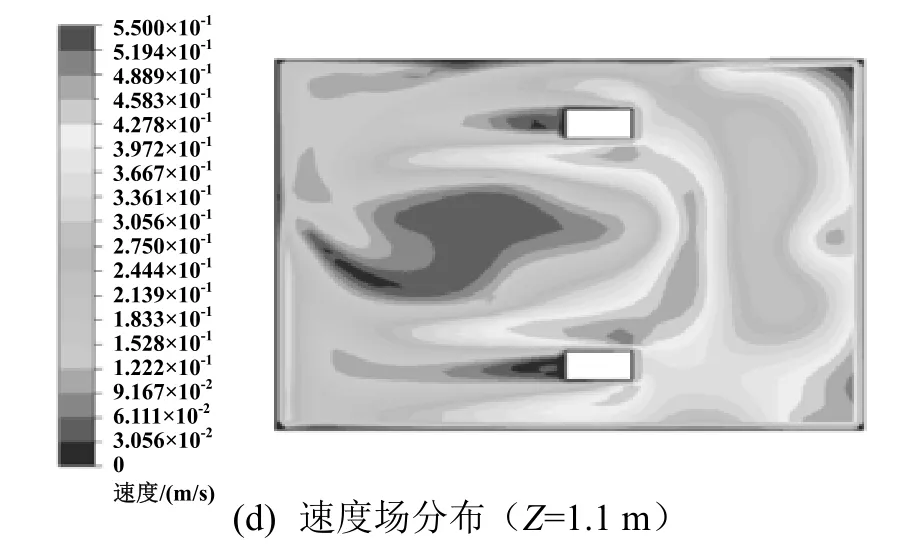
圖5 對開角度為20°時溫度和速度分布云圖

圖6 對開角度為30°時溫度和速度分布云圖

圖7 對開角度為45°時溫度和速度分布云圖

3.2 室內熱舒適性評價——PMV評價

預測平均熱感覺指標PMV，是丹麥FANGER教授在人體熱平衡方程的基礎上，通過收集1,396名受試者的冷熱感覺資料后，提出的用于評價人體熱舒適性的一個數值指標[22]。

ISO以及ASHRAE等組織依據FANGER教授的PMV-PPD指標，規定室內熱環境的舒適標準為-0.5＜PMV＜0.5，相應的PPD為PPD＜10%。而我國很多學者認為,上述指標要求太高，在我國大部分地區難以實現，而且亦無必要。所以一般認為可以接受舒適熱環境的PMV為-1.0＜PMV＜1.0，相應的PPD小于26%。因此，通過FLUENT中相應的功能，將PMV值超過小于-1或大于1的區域切除。圖8為不同對開角度下截面Z=1.1 m處的PMV云圖。

觀察云圖容易發現，對開角度為20°時，截面的PMV值基本上全部位于-1～1之間，并且PMV值分布也較為均勻，在工作人員附近的PMV值大部分位于-0.4～0.4，PMV接近1或-1的區域也很少，熱舒適性在水平面上是4種對開角度中是最好的；當對開角度為0°時，左下角有小塊區域不符合要求，結合圖4(b)的風速分布分析，由于送風口垂直于風口送風，導致左下角和右上角均出現送風死角，而外墻的溫度較內墻高，這才導致了左下角的PMV值過大；當對開角度為30°時，靠近外墻的工作人員附近以及外墻附近有一部分不符合；當對開角度為45°時，整體上是符合要求的，但是工作人員附近有小部分區域偏離設定值。

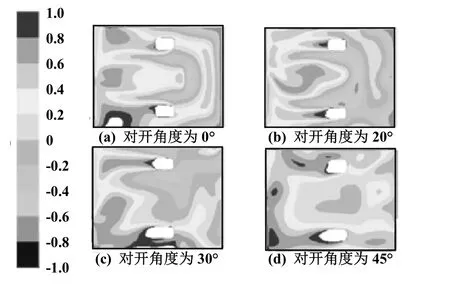
圖8 不同對開角度下截面Z=1.1 m處的PMV云圖

為進一步分析室內垂直方向上的熱舒適性，選取Y=1 m（工作人員附近）截面處的PMV云圖進行分析。圖9是不同對開角度關于截面Y=1 m處的PMV云圖。

觀察圖9可以看出，在側送側回的通風方式下，氣流從上部沿直線方向進入室內，部分冷空氣從風口進入房間以后，逐漸沉降地面，另一部分冷空氣沿著循環路徑與室內空氣進行換熱，然后受熱力影響上升到房間上部，形成下部適中，中上部稍暖的空氣分層現象。這種現象同樣反映到PMV值上，即房間中上部的PMV值高，下面的偏低。并且可以看到，對開角度為20°時，除去接近天花板處的PMV過低之外，其余區域的PMV值的分布是非常均勻的，而天花板附近并不是工作區，所以在垂直方向上同樣是20°度最為合理。

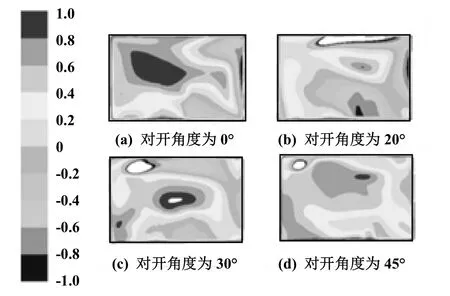
圖9 不同對開角度關于截面Y=1 m處的PMV云圖

分析對開角度為0°的截面，新風射流從風口進入室內以后，它與周圍靜止流體之間存在速度不等的間斷面，間斷面一般會受到不可避免的干擾，從而失去穩定而產生渦旋，卷吸周圍流體進入射流，同時不斷移動、變形、分裂產生紊動，其影響逐漸向內外兩側發展形成自由紊動的混合層。卷吸和摻混的結果就導致射流斷面不斷擴大，而流速則不斷降低，流量沿程增加。在這期間，部分低溫氣流向下沉降，較多的氣流仍繼續沿著原來的方向繼續流動，最終撞擊到墻壁，致使大部分氣流沿墻壁向下流動，沿地板回流至回風口。而工作人員的工作區域偏離中軸面較遠，冷空氣進入室內后，大部分氣流的循環路徑都是圍繞在中軸面附近，只有少部分氣流能夠循環經過工作人員上方，吸熱有限。而且剛剛從風口出來的射流由于速度較快，冷氣流沉降時間有限，氣流向下沉降的不多，但射流軸心速度衰減較快，所以后半段的冷空氣沉降要比前半段多，這就解釋了為何截面左中部的PMV偏高。

3.3 能耗分析

根據模擬的結果，導出4種工況下各壁面的熱流量，匯總于表1。

對比4種工況的熱流量，可以發現，不同工況下各壁面熱流量相差較大。由于4種工況下，只有對開角度不同，其余各條件都是相同的，除了前后壁面有熱流的進出，其它四面都是絕熱面，沒有熱流量的進出，所以前后壁面的熱流量的高低可以用來定性地分析該房間的能耗。工況二（20°）的熱流量是最少的，工況一（0°）熱流量最多。這說明，在對開角度為20°的情況下，房間的能耗是最小的，當對開角度為0°時，能耗是最大的。并且可以發現，隨著送風角度的變大，總熱流量是先減小后增加的，可能在0°～30°下存在一個極小值。

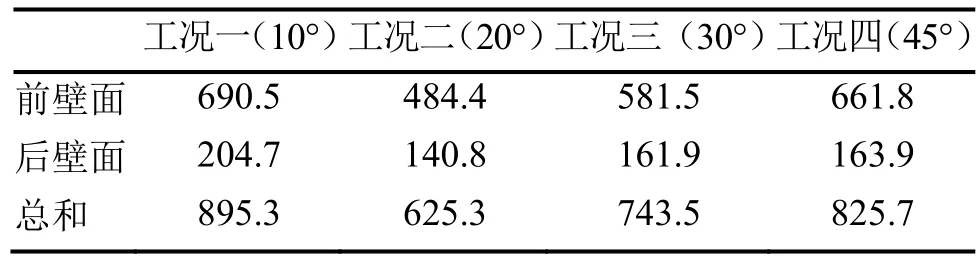
表1 不同工況下壁面的熱流量（W）

4 結論

本文通過對夏季一典型辦公室內流場進行數值模擬，比較百葉風口在不同對開角度下室內溫度場、速度場、PMV分布以及能耗，得出以下結論：

1）通過數值模擬，得到了室內溫度場、速度場及PMV熱舒適性指標，根據這些指標可以對室內熱舒適性進行直觀且科學合理的預測和評價；

2）通過定性分析4種工況下的能耗，得出當對開角度為20°時的能耗是最低的。并且發現隨著送風角度的變大能耗隨之變化的規律，在0～30°，可能存在一個對開角度，使能耗最低；

3）本文通過對比4種工況，對特定模型下室內熱舒適性進行比較，得出當對開角度為20°時，室內溫度以及速度分布比較均勻，熱舒適性是最優的，并且能耗最小。而對于其他的對開角度，或多或少都存在部分區域不符合標準。

由于條件所限，本文未對模擬數據進行實驗驗證，但本文的模擬結果可以為相關工作人員提供借鑒，為優化室內流組織設計提供了理論依據和科學指導，從而優化室內的氣流組織設計。

[1]中華人民共和國建設部. 采暖通風與空氣調節設計規范[S]. GB 50019-2003. 北京: 中國建筑工業出版社,2003: 9-20.

[2]DAGHIGH R, SOPIAN K. The impact of air exchange effectiveness on thermal comfort in an air-conditioned office[J]. American Journal of Applied Sciences, 2009,6(11): 1974-1981.

[3]MAJDOUBI H, BOULARD T, FATNASSI H, et al.Airflow and microclimate patterns in a one-hectare Canary type greenhouse: an experimental and CFD assisted study[J]. Agricultural and Forest Meteorology,2009, 149(6):1050-1062.

[4]曹建偉. 置換通風空調室內空氣品質的數值模擬研究[D]. 北京: 北京交通大學, 2007.

[5]劉敏, 李明海, 盧明, 等. 空調辦公室熱環境數值模擬研究[J]. 土木建筑與環境工程, 2015, 37(S1): 28-31.

[6]鐘武. 夏季辦公室空調房間氣流組織的數值模擬[J].制冷與空調, 2011, 25(3): 304-308.

[7]李朝妹, 張振彬. 空調安裝位置對辦公室室內溫度的影響[J]. 建筑節能, 2011, 39(11): 16-18.

[8]孫建麗, 劉秀玉. 基于FLUENT的空調送風角度對房間舒適性及能耗的影響[J]. 建筑節能, 2015, 43(4):21-24.

[9]吳顯慶, 錢付平, 闞竟生, 等. 通風方式對室內熱舒適性影響的數值模擬[J]. 制冷與空調(四川), 2015, 29(1):16-21.

[10]沈凱, 吳喜平, 宋潔, 等. 某地鐵站廳不同送回風方式的氣流組織數值模擬和分析[J]. 制冷技術, 2010, 30(1):28-32.

[11]劉天驕, 吳經偉, 臧建彬. 通風格柵類型對高速列車設備艙通風散熱特性的影響[J]. 制冷技術, 2017, 37(3):58-62.

[12]俞國華. 變風量空調室內氣流組織的數值模擬[D]. 西安: 西安建筑科技大學, 2004.

[13]喻繼平, 何媛, 趙玉嬌, 等. 基于氣流組織CFD優化的某報社印刷車間空調系統設計[J]. 暖通空調, 2012,42(11): 113-118.

[14]申健, 楊長青, 高小攀, 等. 一種新型組合式風口分層空調氣流組織形式研究[J]. 建筑科學, 2017, 33(8):83-89.

[15]曠金玉, 羅卓英, 周猛, 等. 百葉風口空調房間室內熱環境的數值模擬研究[J]. 科學技術與工程, 2012, 12(2):353-357.

[16]JURELIONIS A, GAGYT? L, PRASAUSKAS T, et al.The impact of the air distribution method in ventilated rooms on the aerosol particle dispersion and removal:The experimental approach[J]. Energy and Buildings,2015, 86: 305-313.

[17]趙彬, 李先庭, 彥啟森. 置換通風的數值模擬[J]. 應用力學學報, 2002, 19(4): 75-79.

[18]趙彬, 李先庭, 彥啟森. 室內空氣流動數值模擬的N點風口動量模型[J]. 計算力學學報, 2003, 20(1): 64-70.

[19]趙彬, 李先庭, 彥啟森. 室內空氣流動的簡捷數值模擬方法[J]. 暖通空調, 2003, 33(3): 102-104.

[20]傅斌, 李曉冬. 室內氣流數值模擬中對方形散流器送風口的描述方法[C]// 全國暖通空調制冷2002年學術年會資料集, 2002.

[21]婁君. CFD風口模型的研究與應用[D]. 成都: 西南交通大學, 2012.

[22]羅淵, 徐文華. 平均輻射溫度對睡眠環境人體熱舒適的影響[J]. 制冷技術, 2010, 30(4): 52-56.