Wiener指數，Hyper-Wiener指數，Harary指數與圖哈密頓性

任麗芳，余桂東，李星星

（安慶師范大學數學與計算科學學院，安徽安慶246133）

設G=（V，E）為n階簡單連通圖，其頂點集V=V(G)={v1,v2,…,vn}，邊集 E=E(G)為 V的二元重集構成的集合。稱E中元素{u,v}(u≠v)為G的邊，邊{u,v}簡記為uv。頂點v的度dG(v)是指G中與v關聯的邊數，G的最小度記為δ。G中vi到vj最短路的長度，定義為vi與vj之間的距離，記作dG(vi,vj)。如果圖G的每個頂點的度均為n-1，則稱G為完全圖，記作Kn。如果圖G=(V,E)的頂點集V可以被劃分為互不相交的子集X和Y，使得V=X?Y且任意邊e={u,v}均滿足u∈X,v∈Y或u∈Y,v∈X，則稱G為二部圖，記作G=(X,Y;E)。若 ||X =p， ||Y=q，并且X中所有頂點與Y中所有頂點都相鄰，則稱G=(X,Y;E)為完全二部圖，記作Kp,q。設G1=(V1,E1)與G2=(V2,E2)是兩個頂點不交的簡單圖，它們的并圖為G1?G2=(V1?V2,E1?E2)，又記為 G1+G2；若 G1=…=Gk，用 kG1來表示G1?…?Gk；它們的聯圖為G1∨G2=即在G1? G2中添加由G1中每個頂點到G2中每個頂點的邊所得的圖。一條包含圖G中所有頂點的路稱為哈密爾頓路。如果圖G中任意兩頂點都由一條哈密爾頓路相連，則稱G是哈密爾頓-連通的。如果圖G含有從任意一點出發的哈密頓路，則稱G從任意一點出發都是可跡的。

連通圖G的Wiener指數W(G)[1]，是指G中任意兩個頂點的距離之和，即

圖G的hyper-Wiener指數[2-3]作為Wiener指數的推廣，記為WW(G)，

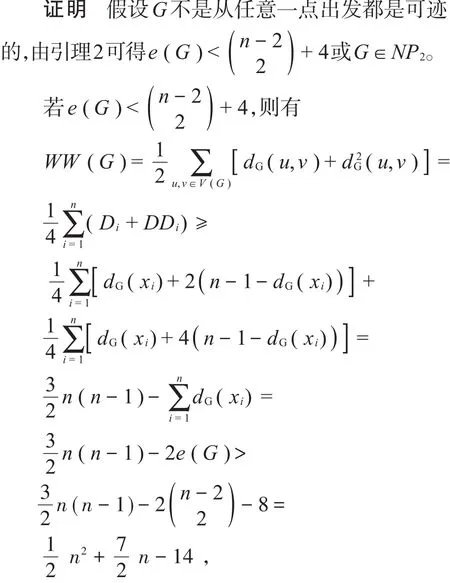
這與定理條件WW(G)

若G∈NP，由引理2知，G不是從任意一點2出發都是可跡的。

定理6 設G為n階連通圖，n≥5，δ≥2，如果H(G)≥則G是從任意一點出發都是可跡的，除非G∈NP2={K2∨(Kn-4+

證明 假設G不是從任意一點出發都是可跡的，由引理2可得

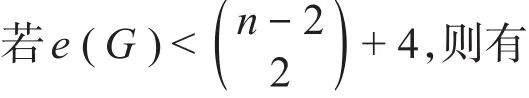
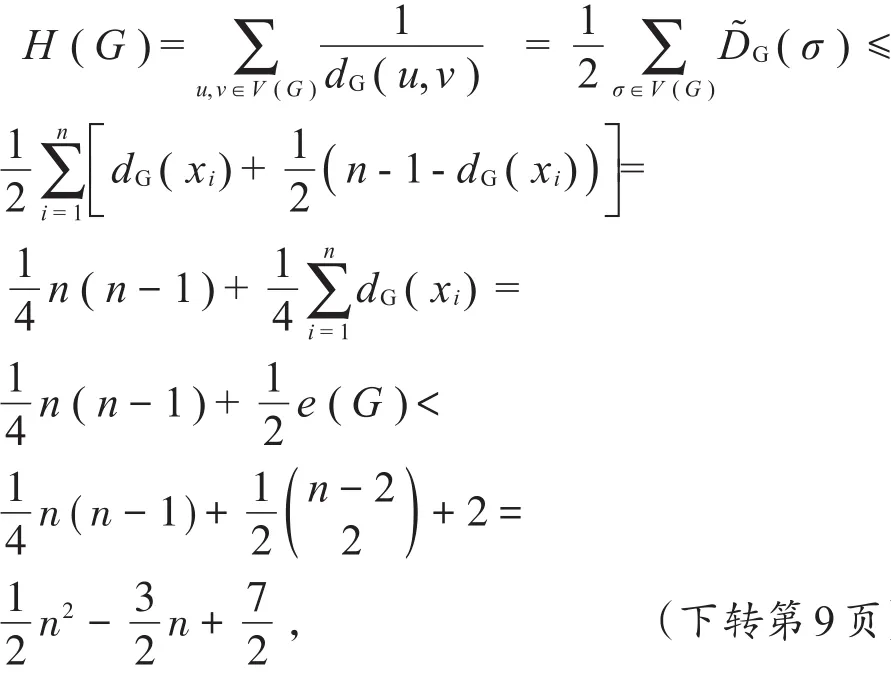
這與定理條件H(G)≥若G∈NP2，由引理2知，G不是從任意一點出發都是可跡的。

[1]WIENER H.Structural determination of paraffin boiling points[J].Journal of theAmerican Chemical Society,1947,69(1):17.

[2]RANDIC M.Novel molecular descriptor for structure-property studies[J].Chemical Physics Letters,1993,211(4-5):478-483.

[3]KLEIN D J,LUKOVITS I,GUTMAN I.On the definition of the hyper-Wiener index for cycle-containing structures[J].Journal of Chemical Information&Modeling,1995,35(1):50-52.

[4]PLAVCHECKSIC D,NIKOLIC S,TRINAJSTIC N,et al.On the Harary index for the characterization of chemical graphs[J].Math Chem,1993,12(1):235-250.

[5]IVANCIUC O,BALABAN T S,BALABAN A T.Reciprocal distance matrix,related local vertex invari-ants and topological indices[J].Math Chem,1993,12(1):309-318.

[6]ZHOU Q,WANG L.Some sufficient spectral conditions on Hamilton-connected and traceable graphs[J].Linear and MultilinearAlgebra,2017,65(2):224-234.